750 kV 变电站构架柱顶避雷针及地线柱结构风洞试验研究

朱殿之 郑海涛 罗 烈 张广平 万 磊 孙先磊

（1.中国能源建设集团甘肃省电力设计院有限公司，兰州730050；2.同济大学土木工程学院，上海200092）

0 引 言

变电站避雷针及地线柱一般设置在构架柱顶，通常采用圆钢管制作，各钢管段之间采用刚性外法兰螺栓连接，是一类主要承受风荷载作用的超细柔高耸结构。近年来，电力行业多次发生变电站避雷针及地线柱结构的风致倒塌的破坏事故［1］（图1），给电力设施的安全运行带来很大的影响。

变电站避雷针及地线柱结构近似为悬壁结构，具有超大高宽比、塔身变截面、刚度及质量沿高度非连续性变化等特点。我国现行《建筑结构荷载规范》（GB 50009—2012）是通过假定结构沿高度变化的质量与宽度的平方成正比和截面刚度变化与宽度的四次方成正比来得到理论的基本周期、振型函数和脉动影响系数等参数，这一假定对自立式高耸结构并不一定成立［2］。为研究变电站构架柱顶避雷针结构的风振响应特性，并检验现行设计方法的可靠性，本文针对西北地区某750kV构架柱顶避雷针结构进行了气动弹性模型风洞试验，获得结构的动力特性、顺风向风振响应和风振系数。

图1 变电站避雷针倒塌事故Fig.1 Failure of lightning rod in substation

1 工程背景

该750 kV电站位于河西走廊的西端戈壁滩，设计风速为31.8 m∕s。避雷针及地线柱位于标高18.8 m构架顶，为Q235B钢材多节段变直径钢管结构，节段间采用刚性外法兰普通螺栓连接（图2），管段几何尺寸及质量参数见表1。

表1 管段几何尺寸及质量Table 1 Geometry and weight of pipe segments

2 试验方案

2.1 相似准则

地线柱及避雷针结构体系气弹模型风洞试验必须满足的相似性条件可以用表2中的无量纲参数来表示［3］。表中，参数ρ表示空气质量密度，取ρ=1.225 kg∕m3；U表示平均风速；B表示结构特征尺寸（本试验取避雷针及地线柱构件段的直径）；μ表示空气运动黏性系数；g表示重力加速度；f表示结构振动频率；E表示结构材料弹性模量；ρs表示结构材料质量密度；δ表示结构阻尼对数衰减率。本次试验在大气边界层风洞中实施，主要研究结构的顺风向风振响应特性，故对雷诺数相似的要求适度放松。

表2 无量纲参数相似准则Table 2 Dimensionless parameter similarity criterion

2.2 模型的设计与制作

试验在同济大学土木工程防灾国家重点实验室TJ-2边界层风洞进行，风洞高度为2.5 m，结构原型高26.2 m，故采用1∶12的几何缩尺比，风洞堵塞率小于1%。根据表2无量纲参数的相似要求，初步确定风速比为1∶ 12，其余主要物理量相似关系见表3。

表3 模型相似比Table 3 Model similarity ratio

结构原型是钢管结构，如完全模拟原型截面形式则模型的壁厚太薄，难以加工。故采用Q235钢核心棒模拟结构刚度，以挤塑式聚苯乙烯板制作外衣模拟结构外形和横向尺寸。

2.3 试验工况

试验对象为悬臂杆结构，在水平面内中心对称。为消除模型的制作误差对试验结果的影响，利用结构的平面对称性，取试验风攻角为0°和90°，对比模型两个正交主轴方向的自振特性和风振响应。试验时，通过安装在参考点处的皮托管以及与之连接的微压计监控风速，参考点位于模型前上方，离地面约2.1 m，相当于实际结构25.2 m高处。由于原结构设计风速为33.0 m∕s（原结构10.0 m处），根据B类地貌风剖面函数计算实际结构25.2 m高处的设计风速为36.9 m∕s，根据风速比换算到模型2.1 m高度处对应加载风速为10.64 m∕s，故本试验中取试验风速范围为0～11.0 m∕s，对应实际风速0～36.9 m∕s。

表4 模型设计参数Table 4 Model design parameters

表5 试验风速Table 5 Test wind speed

2.4 整体试验系统

整个试验系统包括试验加载及测试系统、数据采集系统和监控系统（图3）。测量系统包括同济大学自主研发的加速度传感器、HL-C235CE-W高精度激光位移传感器、东方振动与噪声技术研究所生产的6.18盒式采集仪及与其配套的DASP2000 Professional信号采集与分析系统和PC计算机。测振试验的采样频率为200 Hz，采样时间间隔为0.005 s，采样时长120 s。

图3 试验系统流程图Fig.3 Test system flow chart

2.5 测点布置方案

沿模型高度共布置5个测点，分别采集各测点的顺风向及横风向位移响应以及1、2测点的加速度响应。布置方案见表6。

表6 位移及加速度传感器布置方案Table 6 Displacement and acceleration sensors arangement

图4 激光位移计安装位置Fig.4 Laser displacement meter installation

2.6 风场模拟

试验紊流流场要求按《建筑结构荷载规范》（GB 50009—2012）以1∕12的几何缩尺比进行模拟。B类地貌，地貌指数取∝=0.14。风洞参考风速点离洞底板0.8m，参考风速为6.0 m∕s。在风洞试验段入口处设置2块尖劈，并在风洞底壁上布置尺寸为6 mm×7.5 mm×4.5 mm及10 mm×10 mm×10 mm的立方体粗糙元。采用眼镜蛇热线风速测量仪（Cobra Probe）、PC计算机和专用软件来测量风场中不同高度处风速及湍流度。图5为风洞试验实景，风剖面测试结果见图6，湍流度剖面测试结果见图7，其中点线为实测数据，实线为荷载规范规定取值。

图5 风洞试验实景Fig.5 Wind tunnel test

图6 风速剖面模拟Fig.6 Wind speed profile

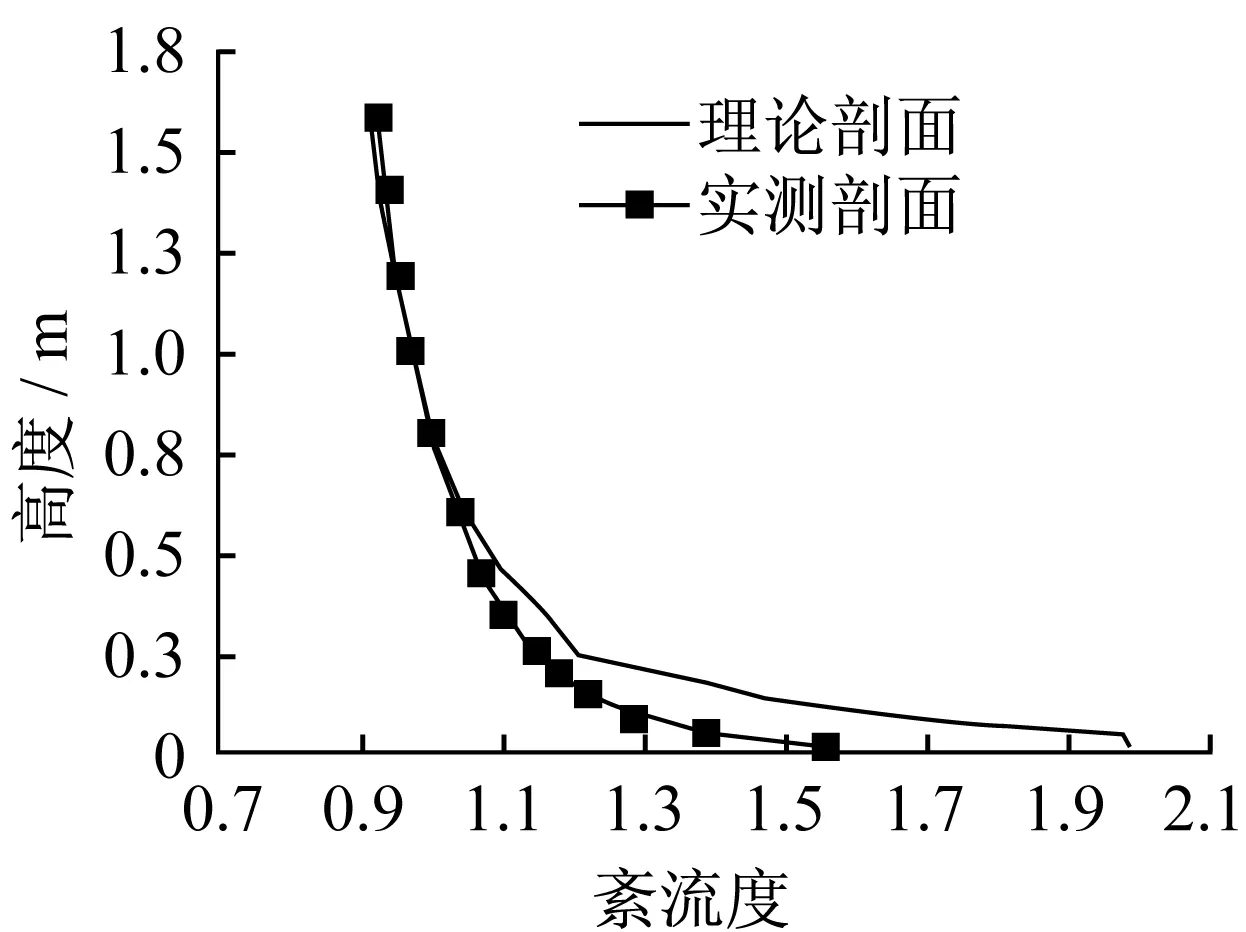
图7 紊流度剖面模拟Fig.7 Turbulence profile

3 试验结果分析

3.1 模型动力特性

模态试验测定的气弹模型基频与经相似关系换算得到的理论数值基本吻合，故气弹模型风洞试验的风速相似系数和其他相似系数可直接按照表7取值，不需进行修正。

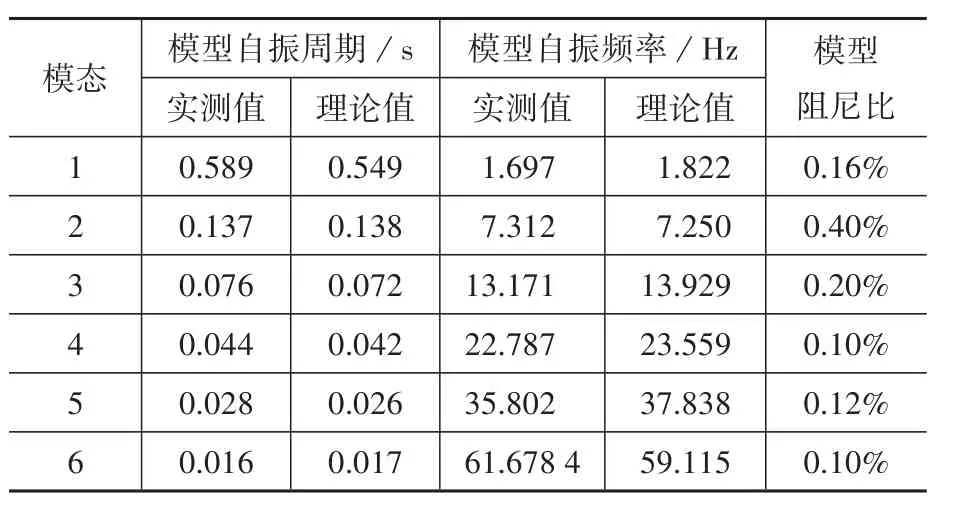
表7 模型模态参数实测值Table 7 Measured modal parameters

3.2 风振位移响应

图8、图9分别为各测点在0～13.5 m∕s试验风速下的顺风向位移均值和最大值。

图8 各测点顺风向位移均值Fig.8 Along-wind mean displacement

图9 各测点顺风向位移最大值Fig.9 Along-wind maximum displacement

由于当顺风向测点位移超过30 mm时会导致横风向激光位移计的激光点完全脱离靶片（考虑到靶片的扰流作用，不能采用过大的靶片），各测点记录到横向位移的风速范围分别为：测点5（0～4.5 m∕s），测点4（0～5.0 m∕s），测点3（0～8.5 m∕s），测点1、2（0～11.0 m∕s）。图10为各测点在0～11.0 m∕s试验风速内横风向位移均值。

图10 各测点横风向位移均值Fig.10 Crosswind mean displacement

图11 各测点横风向位移最大值Fig.11 Crosswind maximum displacement

试验数据表明：

（1）各测点顺风向位移均值、幅值随风速升高，呈抛物线型单调上升；而横风向位移尽管也随风速提高缓慢增大，但同一风速下横风向位移幅值远小于顺风向位移幅值，当风速到达3.5 m∕s以上时，顺风向位移幅值为横风向位移幅值的3倍以上。

（2）横风向位移幅值随风速近似均匀递增，未出现显著的幅值突变状况，可判断试验风速内，模型未出现涡激振动。（图9中风速2.5 m∕s、3.5 m∕s、5.0 m∕s时横风向位移幅值有小幅突变，但图8所示对应的顺风向位移幅值亦有小幅突变，判断此处突变是由于风动风机输出功率不稳定造成的，而非涡激振动的特征）

（3）横风向位移响应均值随风速变化接近0。因此可忽略横风向平均位移响应。

3.3 风振位移响应时程

试验得到了各测点在不同风速下的位移时程曲线及其自功率谱曲线，以下对最大试验风速11.0 m∕s（对应实际设计风速33.0 m∕s）下，各测点顺风向位移时程曲线和其自功率谱曲线（图12）进行分析。

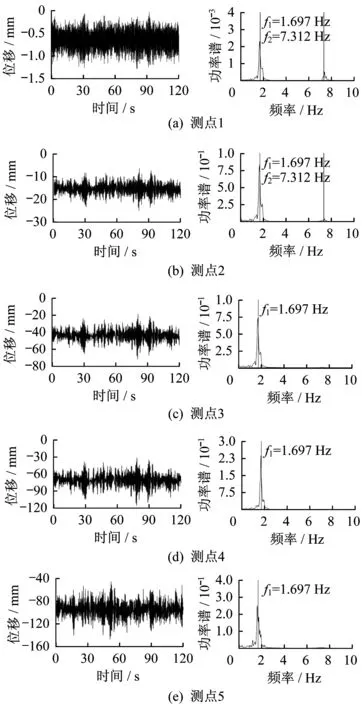
图12 风速11.0m∕s顺风向位移时程及其自功率谱曲线Fig.12 Along-wind displacement time history curve and its self-power spectrum curve v=11.0m∕s

最大试验风速11.0 m∕s时，模型顶部顺风向位移均值为94.5 mm，对应原型顶部位移1 134.0 mm，顺风向位移幅值为147.2 mm，对应原型顶部位移1 766.4 mm。从位移自功率谱曲线可以看出，各测点位移响应仍以一阶振型响应占主导地位，而其他各阶频率成分表现不明显，结构的风致位移主要来自于一阶振型的贡献。

3.4 风振加速度响应时程

将试验所得的位移时程曲线进行2次求导，可以得到加速度时程曲线，再经傅立叶变换后可以得到各个测点的加速度自功率谱曲线。以下对11.0 m∕s风速时各测点顺风向加速度时程曲线和其自功率谱曲线（图13）进行分析。

图13 风速11.0m∕s顺风向加速度时程及自功率谱曲线Fig.13 Along-wind acceleration time history curve and its self-power spectrum curve v=11.0m∕s

从加速度自功率谱曲线可以看出，顺风向的加速度响应功率谱有几个明显的峰值，频率分布较宽。测点3、测点4加速度谱的第一、第二峰值较为接近，加速度响应的第二峰值在模型结构的二阶频率f=7.312 Hz附近；测点1、测点2、测点5的第二峰值显著大于第一峰值。说明高频振动对结构风致加速度响应的贡献显著大于对位移响应的贡献。

4 风振系数

基于MATLAB程序，采用线性滤波法中的自回归（Auto-regressive，AR）模型合成顺风向脉动风荷载时程曲线，通过SAP2000软件对原结构有限元模型进行了时程计算。

在设计风速时，时程分析计算得到的原结构顺风向位移响应幅值与风洞模型试验结果对比见表8。试验结果与有限元计算得到的位移幅值的比值略大于1∕12的几何缩尺比，这是由于模型实测阻尼比（表8）小于有限元计算时的取值（根据《高耸结构设计规范》［4］采用的阻尼比1%）。但两种方法得到的位移幅值仍保持近似线性关系，说明两种方法得到的风振响应具有可比性。

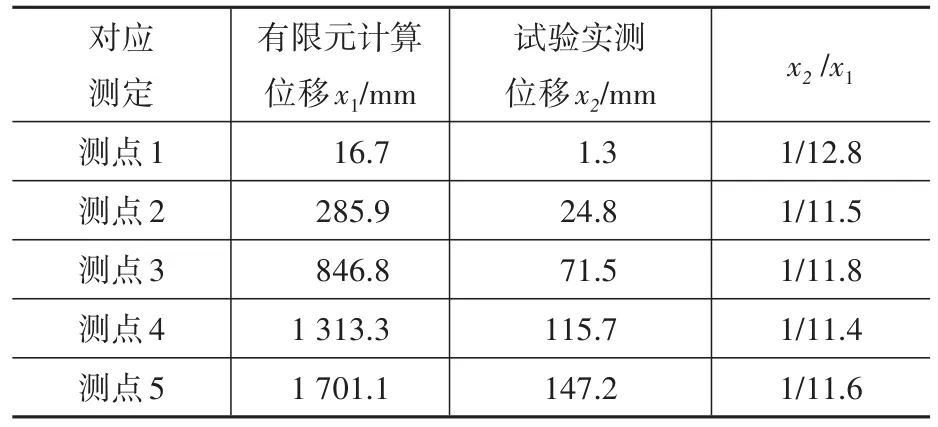
表8 有限元计算位移值与试验结果比较Table 8 Displacement comparision between FEA and test results

分别依据《建筑结构荷载规范》（GB 50009—2012）［5］、《高 耸 结 构 设 计 规 范》（GB 50135—2006）［4］、有限元计算分析数据、风洞试验实测数据计算结构（模型）在设计风速时的风振系数，结果见表9-表12。各方法所得风振系数的比较，见表13及图14。

表9 风振系数计算（《建筑结构荷载规范》）［5］Table 9 Wind vibration coefficient calculation（GB 50009—2012）

表10 风振系数计算（《高耸结构设计规范》2006版）［6］Table 10 Wind vibration coefficient calculation（GB 50135—2006）

比较结果表明，除位于地线柱段的测点1处（构件节段直径最大段）三种方法得到的风振系数较为相近外，其余各测点处有限元法与试验法得到的风振系数均明显高于《建筑结构荷载规范》和《高耸结构设计规范》的取值。

5 结论

通过气动弹性模型试验，得到了750 kV变电站构架柱顶避雷针结构在不同风况下的风致响应，并得到了该工程结构的一些重要受风特性：

表11 风振系数计算（有限元分析）Table 11 Wind vibration coefficient calculation（FEA）

表12 风振系数计算（气弹试验）Table 12 Wind vibration coefficient calculation（Aeroelastic elastic test）

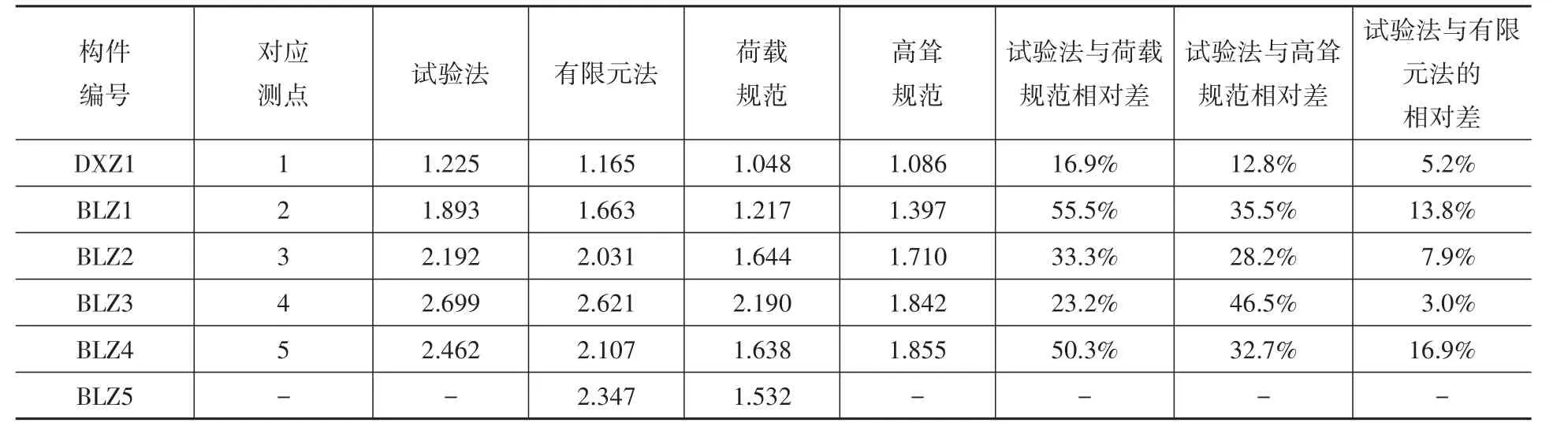
表13 风振系数比较Table 13 Comparision of wind vibration coefficient

图14 各测点风振系数Fig.14 Wind vibration coefficient

（1）模型顺风向位移响应基本来自于一阶振型贡献，顺风向位移均值、幅值随风速升高而呈抛物线型单调上升。

（2）模型低风速下横风向位移响应也基本来自于一阶振型贡献，振动均值基本为0，振动幅值明显小于同风速下顺风向响应。位移幅值随风速升高而近似均匀增大，试验风速范围内未观察到横风向位移幅值突变，试验中模型未发生显著的涡激振动。

（3）高阶振型对顺风向加速度响应贡献显著，各工况下各测点的加速度响应功率谱中均有数个明显峰值，峰值频率分别近似对应结构的前数阶自振频率。

（4）在考虑高阶振型对模型加速度贡献的情况下，计算得到的模型风振系数显著大于现行相关规范的规定取值。