不锈钢芯板楼板试验研究及理论分析

2020-06-17蔡华根刘泽龙

结构工程师 2020年2期

蔡华根刘泽龙

（湖南大学土木工程学院，长沙410082）

0 引言

不锈钢芯板结构是一种新型的建筑结构体系，类似于蜂窝夹层结构，不锈钢芯板由不锈钢面板中间密布不锈钢薄壁芯管组成，采用铜钎焊将芯管和面板焊接成一个牢固的整体，不锈钢芯板示意图如图1所示。不锈钢芯板结构将蜂窝夹层结构这一性能优越的新型结构与不锈钢这一具有良好发展前景的材料有机结合，通过对不锈钢芯板标准件的切割和拼接可以制作成建筑结构中的梁、板、柱、墙等构件，进而用于建筑结构的安装与施工。

目前对于不锈钢芯板结构的研究还处于起步阶段，有大量的工作需要进行，当不锈钢芯板结构作为楼板使用时，其主要受力形式为四边支承下承受竖向均布荷载。不锈钢芯板结构的受力机理与蜂窝夹层结构的十分相似，蜂窝夹层结构受弯时，由于上下面板较薄，主要承受平面应力，芯子主要承受剪切作用，但不锈钢芯板结构面板较厚，芯子排布方式也与传统蜂窝夹层板有较大区别，因此对不锈钢芯板结构的抗弯性能进行研究是很有必要的。

图1 不锈钢芯板Fig.1 Stainless steel core plate

对不锈钢芯板结构的研究可以参照蜂窝夹层结构的研究方法，国内外学者对蜂窝夹层结构弯曲性能的研究有很多，主要的试验方法有三点弯曲试验和四点弯曲试验［1-3］。而对于常规楼板结构的试验方法主要是四边支承静力堆载试验［4］，蜂窝夹层板在该试验方法上的研究还较少。本文对两块不锈钢芯板四边简支板进行单调静力堆载试验，并建立了相应的有限元模型，对不锈钢芯板结构的受力特性进行了理论分析。结合条带法和虚功原理推导不锈钢芯板四边简支板在均布荷载作用下的跨中挠度简略计算公式，对比了公式计算与有限元计算的结果验证了公式的合理性。

1 试验研究

1.1 试件设计

本试验共设计2种不同的足尺试件，每种试件数目为1个，共计2个试件，试件由远大可建科技有限公司研发生产提供。试件面板和芯管的材料均为奥氏体S30408不锈钢，面板厚度均为1.5 mm，芯管排布间距均为121 mm×100 mm，其中X轴方向间距为100 mm，Y轴方向间距为121 mm。由于生产工艺决定了不锈钢芯板单块标准件为2 m宽，因此B1试件由两块4 000 mm×2 000 mm的芯板构件（即两块B2试件）拼接而成，B2试件是一块单独的4 000 mm×2 000 mm的芯板构件。试件具体规格参数情况详见表1。试件实物图如图2所示。

图2 试件实物图Fig.2 Specimen

1.2 试验方案

1.2.1 加载装置

试验加载装置如图3所示，包括由H型钢梁组成的刚性框架加载台、钢垫板、钢管滚轴等，钢垫板和钢管组成滚动铰支座。

表1 试件尺寸及规格参数Table 1 Specimen size and specification parameters

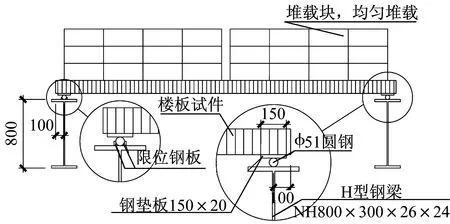
图3 加载装置剖面示意图Fig.3 Section diagram of loading device

1.2.2 加载方案

正式加载前先进行预加载，检查仪器的工作状态是否正常。正式加载时，根据现场堆载物的规格和试验前有限元试算，采用每级1.32 kN∕m2的分级进行堆载。事先对试件板面进行区格划分，堆载物采用梅花式插空摆法。堆载铁块的行与行之间、列与列之间都留一定的空隙，且板边到支座线范围内不堆载，B1试件取计算跨度为3 800 mm×3 800 mm，B2试件取计算跨度为3 900 mm×1 900 mm。根据现场试验条件尽量堆载，直至试件破坏或者继续加载难度过大。

1.2.3 测点布置

本次试验竖向位移测量的主要内容为板底1∕4板格范围内的特征点的挠度采集，特征点位置及编号如图4所示，其中B1试件板的2号挠度测点位置由早先的有限元模拟试算而确定，为理论最大挠度点。支座四周也架设百分表，采集支座竖向沉降，以便对挠度进行修正。应变测量内容主要为试件面板的几个主要特征点，用于后续验证有限元模拟的准确性。现场试验情况如图5所示。

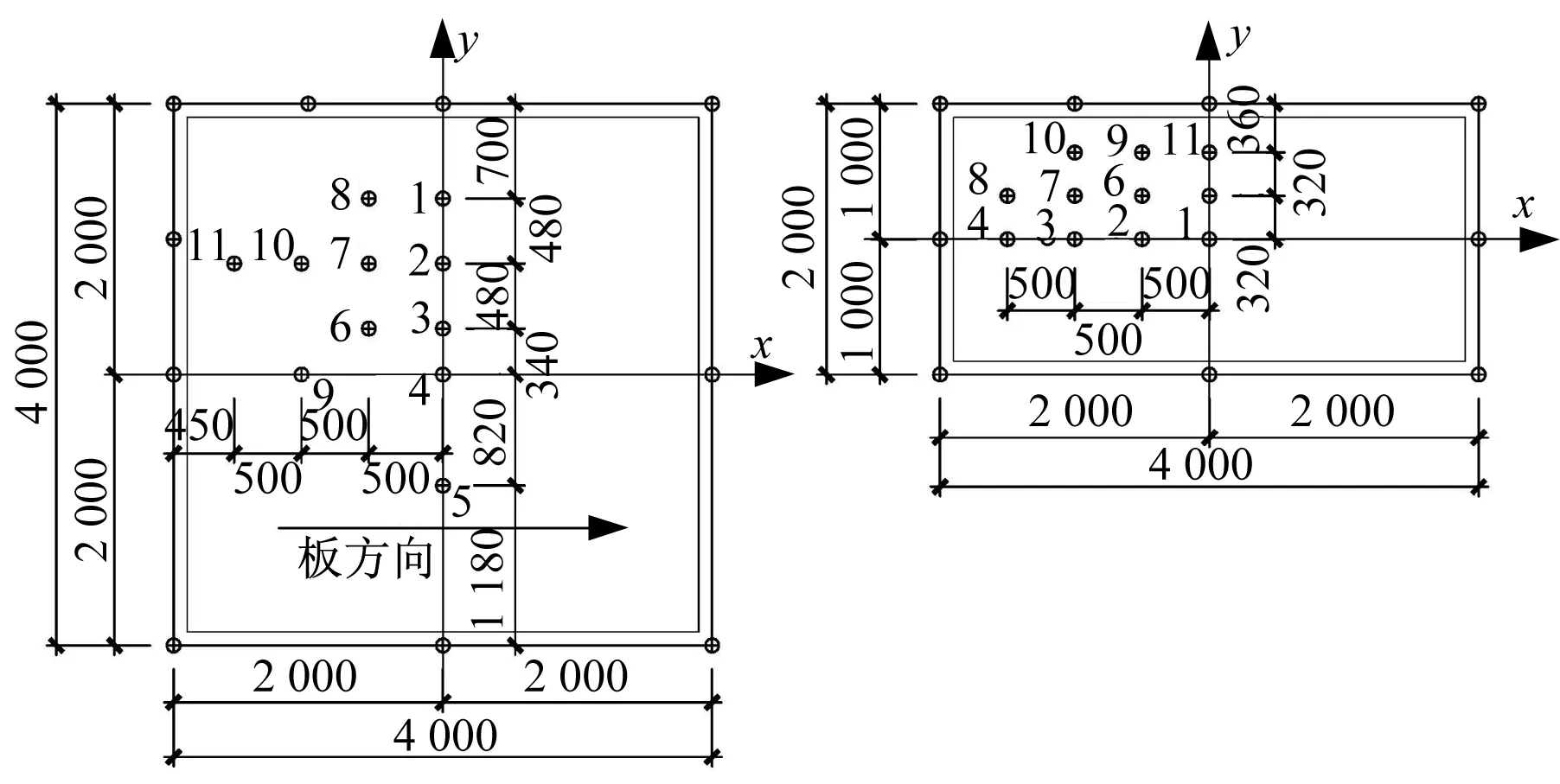
图4 试验试件及测点布置（单位：mm）Fig.4 Specimens and deflection measuring points（Unit：mm）

1.3 试验结果及现象分析

图5 现场试验情况Fig.5 Experiment process

根据堆载试验实测的数据，以试件板底1∕4板格范围内X轴方向测点的竖向位移为水平坐标，试件所承受的均布面荷载为竖向坐标，绘制各试件的荷载-竖向位移曲线。试件堆载试验的荷载-竖向位移曲线如图6所示。

图6 荷载-竖向位移曲线Fig.6 Load-deflection curve

由图6可知，挠度和荷载一直呈现线性关系变化，加载过程中试件整体处于弹性状态，曲线末端斜率有小量变化，试件塑性发展不明显。从试验数据利用线性插值可推测，B1试件加载到11.945 kN∕m²时，最大挠度达到19 mm，是板跨度的1∕200，即达到正常使用极限状态。B1试件加载到32.243 kN∕m²时，最大挠度达到50.759 mm，是板跨度的1∕75，未达到1∕50，即未达到承载力极限状态。B2试件加载到7.688 kN∕m²时，最大挠度达到9.5 mm，是板跨度的1∕200，即达到正常使用极限状态。B2试件加载到32.827 kN∕m²时，最大挠度达到38.990 mm，是板跨度的1∕49，超过1∕50，即达到了承载力极限状态。

在对各试件进行的堆载试验过程中，试件均无明显破坏现象，结构表现稳定。堆载的后期过程中，上下面板靠近边界的区域均可以观察到面板的波浪形褶皱变形，最后一级堆载后该变形较为明显，如图7所示。这是因为板边沿为剪力最大的区域，剪力在相邻芯管间面板产生的次弯矩引起的弯曲变形在该区域较为明显。试件卸载后经过一段时间的观察，面板边缘区域的波浪形褶皱变形没有完全恢复平整，可判断面板该区域已发生轻微的塑性变形。后续对试件切割后观察芯管情况，芯管没有明显的变形破坏现象，芯管与面板之间的铜钎焊连接处均未出现开裂脱焊的现象。由此推断，芯板结构作为楼板使用时，极限状态主要由挠度控制，芯板的破坏为上下面板局部屈服破坏，破坏区域为面板靠近支座的边沿区域，设计使用时以挠度计算为主，屈服弯矩计算作为参考。

图7 上下面板的波浪形褶皱变形Fig.7 Undulating drum deformation of the upper and lower panels

2 有限元模拟分析

这部分通过ABAQUS有限元分析软件建立有限元模型对上述试验过程进行模拟，并将有限元模拟结果与试验结果进行对比，验证有限元模型的准确性。

2.1 建立模型

建立了两个有限元模型，分别与试验的两个试件相对应，尺寸规格以及各种几何参数均与试件相同，取编号为BY1，BY2。

模型的主要部件包括面板、芯管、边缘板件，以及支承试件四边的钢垫板，其中面板、芯管和边缘板件采用S4R四节点二次减缩积分壳单元模拟，钢垫板采用C3D8R八结点线性减缩积分六面体单元模拟。模型涉及两种材料：面板、芯管和边缘板件的材料为奥氏体S30408不锈钢，支座钢垫板的材料为Q345钢，由于钢垫板并非本文的主要研究对象，因此其本构关系简单采用理想弹塑性模型，泊松比取0.3，弹性模量取2.06×105MPa。奥氏体S30408不锈钢的本构关系根据材料的力学性能试验确定，将材性试验试件与堆载试验试件B1和B2放入同一钎焊炉内经过同一升温降温过程，后通过万能试验机进行材性试验，结果如表2所示。参考文献［5］采用G-N两段线模型［6］按下式进行修正，得到的应力应变曲线如图8所示。

式中：σ为正应力；ε为应变；n材料应变硬化系数；E0为材料弹性模量；σ0.2为材料名义屈服强度；εt0.2为应力σ0.2对应的应变值；σ0.01为对应塑性应变0.01%的应力，一般取其为材料的比例极限强度；σ1.0为对应塑性应变1.0%的应力；E0.2为对应于名义屈服强度σ0.2处的切线模量；n′0.2，1.0为σ0.2与σ1.0之间应力-应变曲线的材料应变硬化系数。

表2 S30408奥氏体不锈钢材性试验所测强度指标Table 2 S30408 austenitic stainless steel strength index measured by material tests

拟合得到的S30408不锈钢本构关系曲线为工程应力-应变曲线，换算成真实应力-应变曲线后输入到ABAQUS材性设置中。

模型上面板施加垂直于板面的竖向均布荷载，面板边缘部分不加载。对钢垫板底面划分中线，并在该中线添加边界条件。计算方法采用ABAQUS的“静力，通用”算法分析，同时考虑几何非线性和材料非线性。荷载及边界条件的设置如图9所示。

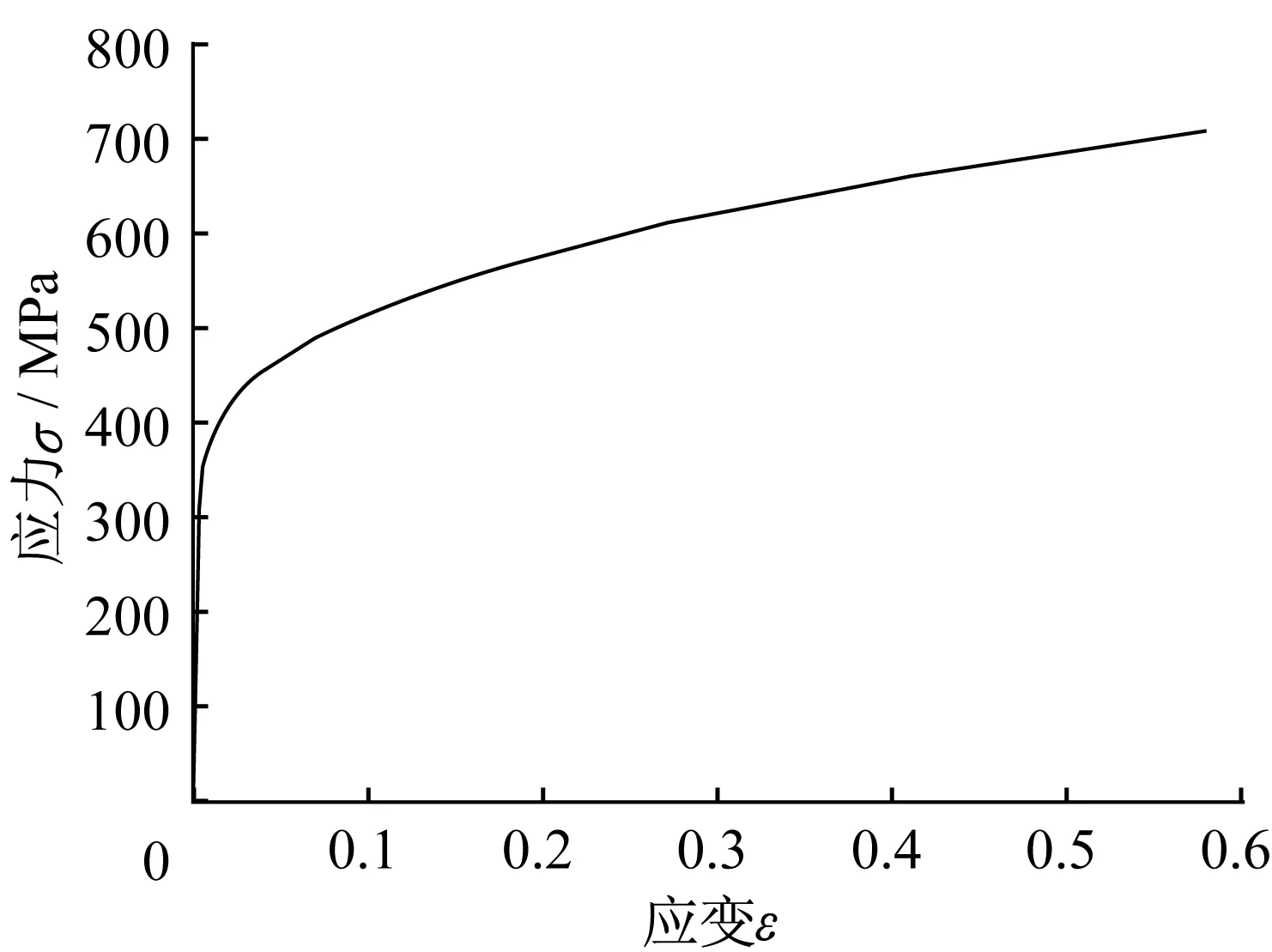
图8 S30408奥氏体不锈钢的应力-应变曲线Fig.8 Stress-strain curve of S30408 austenitic stainless steel

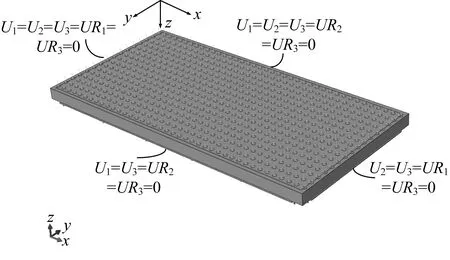
图9 有限元模型荷载及边界条件Fig.9 Load and boundary conditions of finite element model

2.2 有限元模拟结果与试验结果对比

将两个有限元模型计算得到的荷载-竖向位移曲线与相对应的试验的荷载-竖向位移曲线进行对比，挠度最大点对比结果见图10。从以上对比中可以看出，有限元模拟计算得到的荷载-竖向位移曲线与试验得到的荷载-竖向位移曲线吻合良好。

在有限元模拟中，以BY2模型为例，结构整体的挠度变形曲线如图11所示（变形放大系数均为3），上下面板在靠近支座边缘出现了波浪型变形，即出现反弯特征。

由以上对比分析可见，有限元模拟结果与试验结果吻合良好，验证了有限元模拟中所选取的参数的合理性，表明本文所建立的有限元模型能够准确地模拟试验过程，具有较高的参考价值。

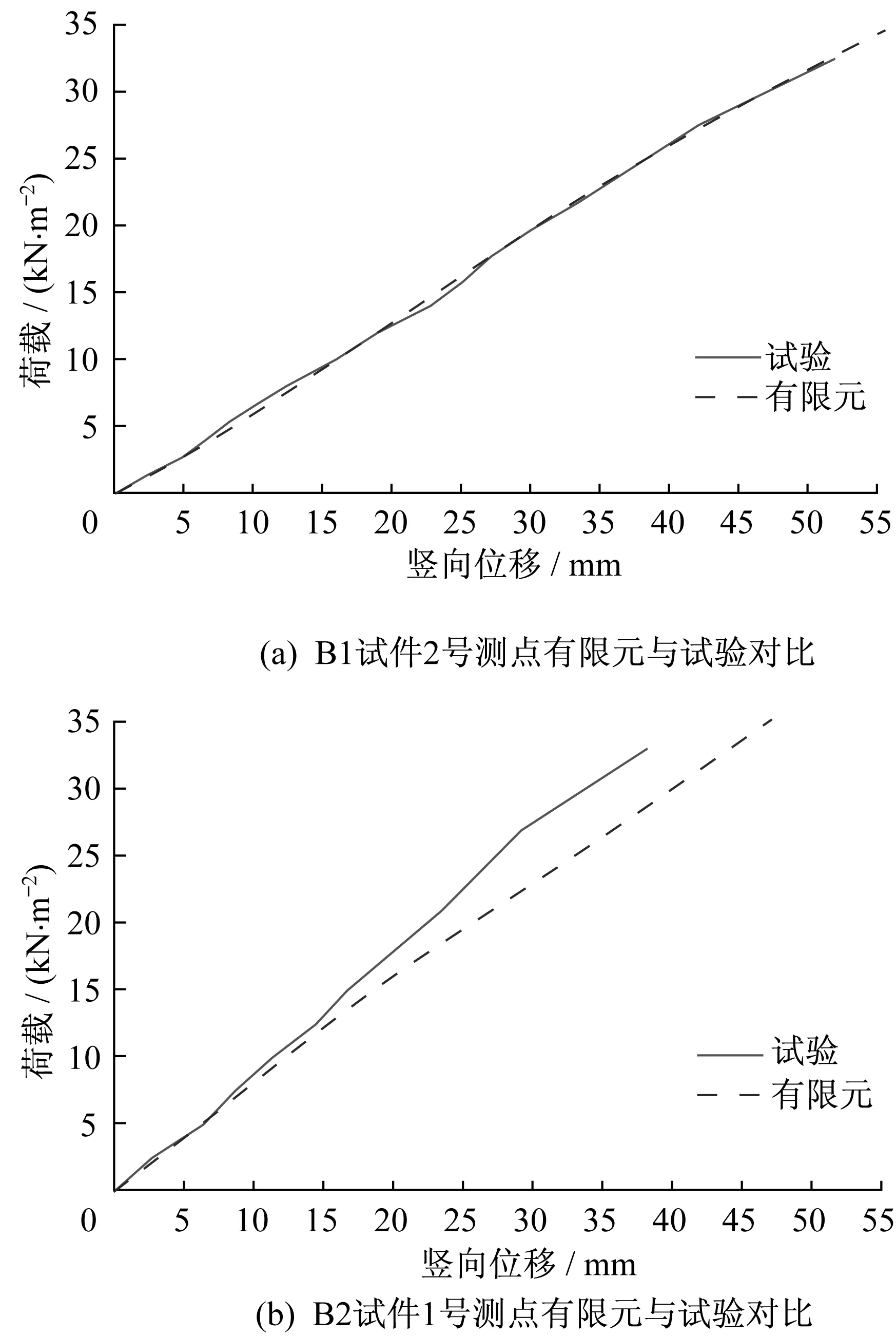
图10 有限元计算结果与试验测量结果对比Fig.10 Comparison of finite element calculation results and experimental measurement results

图11 BY2挠度变形曲线Fig.11 BY2 deflection deformation curve

以BY2模型为例分析四边简支芯板受力过程，图12为正常使用极限状态即竖向荷载为7.688 kN∕m²时BY2有限元模型的等效应力云图，从图中可以看出面板边缘小部分区域与芯管钎焊连接的部分应力分布较为集中，且应力较大，但还未超过S30408不锈钢的屈服强度328 MPa，面板其余部分的应力分布较为均匀，应力大小基本都在145 MPa以下。由图13可以看出大部分芯管应力较小，在54 MPa以下。由此可知，当试件B2结构板的最大挠度达到设计限值时，其不锈钢材料均未达到屈服状态，强度储备充足，实际设计应以挠度控制为主。

图14为BY2有限元模型在竖向荷载为32.827 kN∕m²时的挠度分布云图和变现特征图，表现出明显的双向弯曲特征。对于由两块B2试件拼接的B1试件，拼接处的边缘板件对楼板起到加劲的有利作用，使楼板挠度偏小。有限元模型与试件的变形特征对比，可以看出面板边缘都出现了波浪形褶皱变形，有限元模型和试件的变形特征十分吻合。

图12 正常使用极限状态时整体的Von-Mises应力云图Fig.12 Overall VonMises stress cloud for normal use limit state

图13 正常使用极限状态时芯管的Von-Mises应力云图Fig.13 Core tubes’VonMises stress cloud for normal use limit state

图14 挠度云图和变形特征Fig.14 Deflection cloud and deformation characteristics

3 不锈钢芯板挠度计算的理论分析

3.1 不锈钢芯板的基本设计参数

不锈钢芯板的参数说明：lmx和lny为x和y方向芯管间距；l'mx和l'ny为x和y方向芯管边距；tf为上下面板厚度；h为芯板高度；hw为芯管高度；d为芯管直径；dm为x方向芯管净间距，dm=lmx-d；dn为y方向芯管净间距，dn=lny-d；tw为芯管壁厚；a为芯板x轴方向跨度；b为芯板y轴方向跨度。芯板几何参数示意图见图15。

图15 不锈钢芯板示意图Fig.15 Stainless steel core plate schematic

3.2 条带法

条带法是Hillerborg［7］基于下限法以及边支承板基本理论提出的，有计算简便和适用范围广的优点［8］。本文芯板跨中正交两个方向板条的划分均采用单个芯管区格的宽度，荷载在两个方向的分配按照位移协调原则，即两个方向的板条跨中挠度相同fx=fy，两个方向荷载按式（1）分配：

式中：qx，qy分别为x，y方向上分配到的板面荷载；kx，ky为与x，y两个方向条带的刚度有关的参数；q为板所受的均布荷载。

板条划分方式如图15所示，将板的问题转化为“梁”的问题。划分出来的板条的“腹板”在“梁”长方向并非是连续的，不可按传统实腹梁计算挠度。将条带法划分的单元板条中的面板和芯管简化为刚接杆件进行简化计算，计算简图和计算结果如图16所示，图16（a）中均布荷载已等效为节点荷载，即Pmx=qxlnylmx。图16（b）中上下杆件轴力由结构弯矩产生，图16（c）中上下杆件和中间杆件的弯矩都由结构的剪力产生，可以看出相邻芯管间的面板会出现反弯点，靠近支座边缘板件的弯矩较大，与图10中面板边缘出现波浪形变形相吻合，图16（d）中上下杆件剪力和中间杆件的剪力都由结构剪力产生。

3.3 基于虚功原理的芯板挠度计算理论

经典材料力学中对任意结构体系，位移可按变形体系的虚功原理推导得出，对于仅受荷载作用且无支座移动和温度改变等影响的结构可按下式计算位移：

图16 单元板条的简化计算Fig.16 Simplified calculation of unit slats

划分的单个板条的挠度计算方法可以参考腹板挖孔的蜂窝梁的挠度计算方法，即采用费式空腹桁架法进行简化计算［9］。如图16所示将板条等效为刚接桁架，采用虚功原理计算杆件轴力、弯矩和剪力对桁架跨中产生的竖向位移，即可等效为芯板板条的跨中挠度：

式中：fx为x方向板条的跨中挠度；fNx为图16（b）轴力产生的杆件轴向变形引起的跨中挠度，即上下面板拉伸压缩引起的挠度；fMx为图16（c）弯矩产生的杆件弯曲变形引起的跨中挠度，即面板和芯管转动而引起的的挠度；fQx为图16（d）剪力产生的杆件剪切变形引起的跨中挠度。

3.3.1 轴力挠度fNx的计算

面板较薄，认为面板只受平面力，当将面板等效为杆件时，整体弯矩产生的内力即为杆件的轴力，上杆件（上面板）受压，下杆件（下面板）受拉，如图16（b）和图17（b）所示，即条带的弯曲变形与等效杆件的轴向变形等效。忽略芯管的抗弯刚度，认为芯层只承受横向剪力。按图17单芯管区格可将图16（b）中的轴力由结构的弯矩换算：

按图17（c）计算上下等效杆件轴力：

由结构对称和上下面板受拉压对称可得：

式中，A=tflny；h=tf+hw；q=qxlny。可得：

式中，E为奥氏S30408不锈钢的弹性模量，取193 000 MPa。

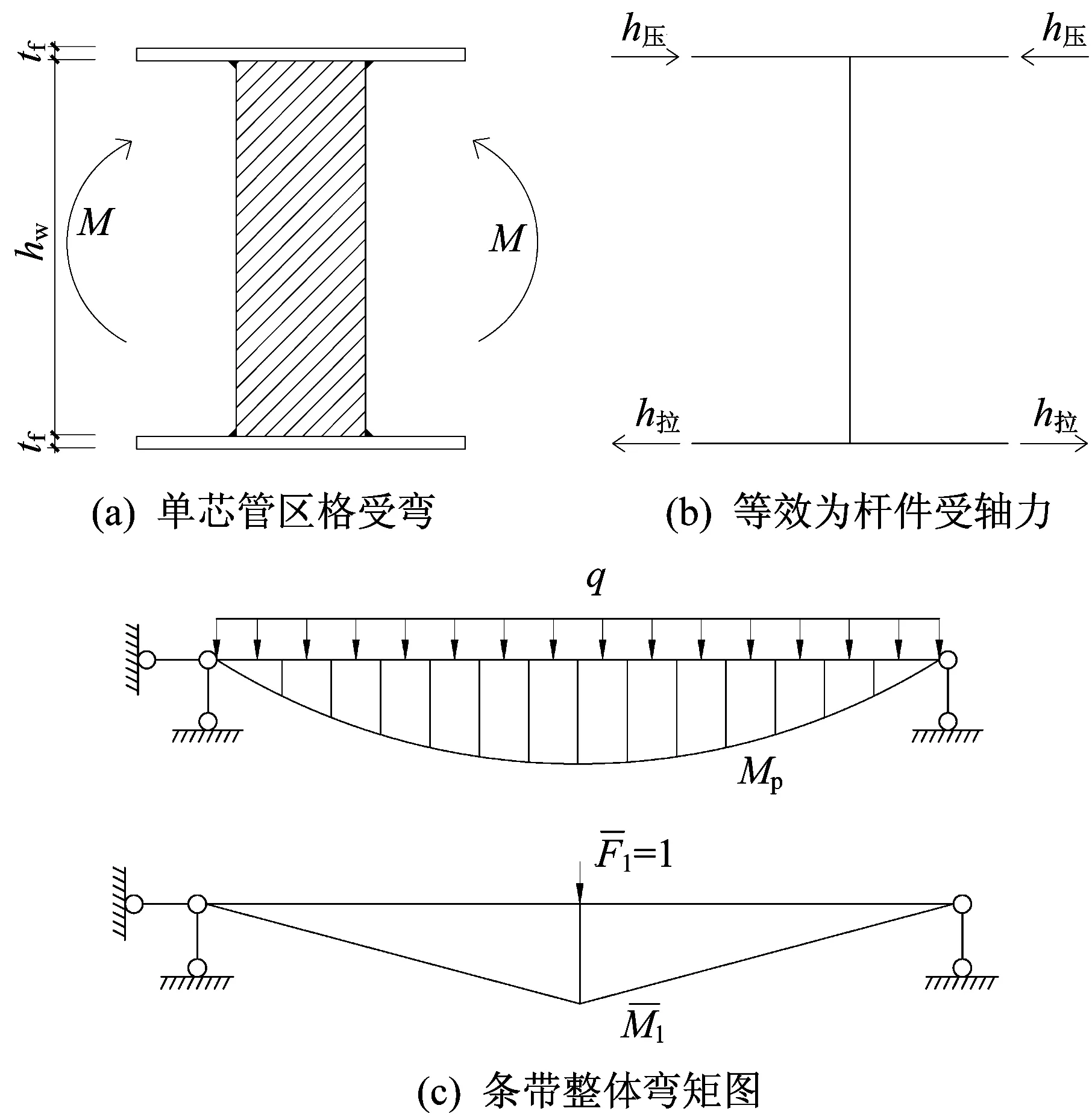
图17 单元板条弯曲变形的计算简图Fig.17 Calculation diagram of bending deformation of unit slats

式（7）也可用实腹梁的形式表示为

3.3.2 弯矩挠度fMx的计算

由于芯层（腹板）在梁长方向并非是连续的，上下面板在受压和受拉的同时还会受到由剪力产生的弯曲，即上下面板等效为杆件时还会受弯，条带的剪切变形与等效杆件的弯曲变形等效，如图16（c）所示。取单个芯管区格进行计算，将费式空腹桁架法的Altfillisch假定［10］适配于芯板可描述为：①截面保持平面变形；②在剪力作用下，没有芯管只有上下面板截面处的总剪力按刚度分配给上下面板，一般情况下上下面板厚度相等，故总剪力平均分配到上下面板；③由相邻芯管间剪力在上下面板引起的次弯矩，反弯点出现在相邻芯管间面板的中心。总剪力按刚度分配给上下面板均为V∕2。将芯板板条视为刚节点桁架，对芯板板条计算模型进行简化，在反弯点位置取铰接，采用静定结构进行计算［9］，如图18所示。

图18 单芯管单元受剪的计算简图Fig.18 Calculation diagram of sheared single core tube unit

图19 为剪力作用下的弯矩图，面板的转动为绕芯管边缘的转动，利用图乘法图乘时芯管宽度d部分的弯矩不参与图乘，可求得面板及芯管转动而引起的挠度fMx：

式中：Vi为单元i所受的剪力；Ifx为按图19计算时面板的截面惯性矩；Ic为按图19计算时芯管的截面惯性矩。

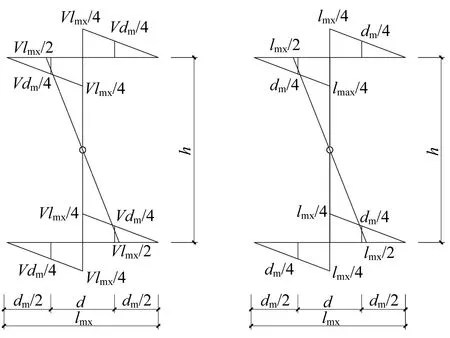
图19 单芯管单元剪力作用下的弯矩图Fig.19 Moment diagram of sheared single core tube unit

二者可按下式计算：

以上分析为单个芯管单元的弯矩产生的挠度。设m为x向芯板板条芯管间隔数量，可得x向芯板板条整体挠度计算公式：

当两边支座条件为简支的板条在竖向均布荷载作用下时，有

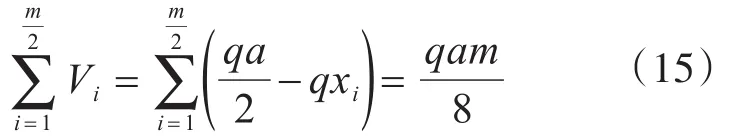
将式（11）代入式（10）可得

由于在计算面板转动时将芯管和面板等效为理想的刚接杆件，实际中单元芯格内面板宽度要比芯管直径大，面板绕与芯管连接处的转动要比等效杆件时要大得多，即式（16）应该修正为

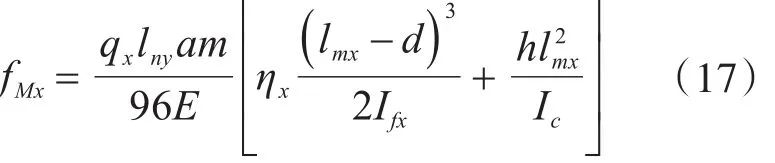
式中，ηx为次弯矩引起面板转动而产生的挠度的扩大系数，具体取值与d/lmx有关，后文通过与有限元计算对比后拟合得出。

3.3.3 剪力挠度fQx的计算

条带的剪切变形与等效杆件的剪切变形等效，如图16（d）所示。fQx的计算可，由图20图乘可得：

式中：k为剪应力修正系数，对于矩形截面取k1=1.2，对于薄壁圆环型截面k2=2；Af为面板截面积；Ac为芯管截面积：

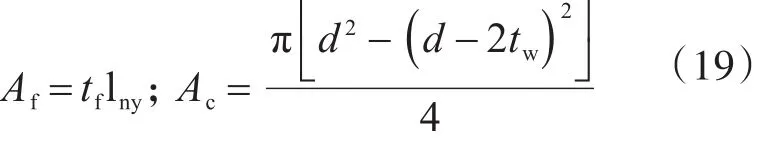
图20 单芯管单元剪力作用下的剪力图Fig.20 Shear diagram of sheared single core tube unit

参考fMx计算过程，可得板条在竖向均布荷载作用下剪切变形：

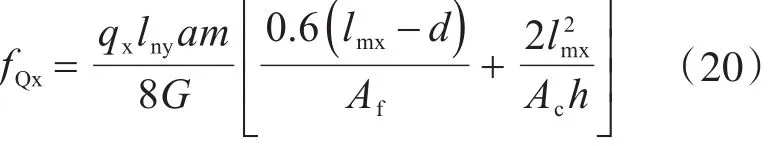
经过试算发现，式（3）中剪切变形fQx相对于其他两项而言要小得多，固可忽略不计。简化式（3）为只取fNx和fMx两项，可得荷载分配系数相关参数kx，ky的计算：

y方向板条的挠度计算同理，仅需将式（20）中各个参数下标中的x换成y，y换成x，计算跨度由a换成b，间距数m换成n即可。

3.4 荷载分配系数的确定

根据上文推导的挠度计算公式，按照位移协调原则，即板的跨中挠度f为

3.5 拟合ηx和d/lmx的线性关系直线

采用有限元软件建立单向单元板条模型，模型如图21所示，通过面板厚度、芯管外径和芯管间距三个对挠度影响最大的参数的不同组合建立了36个计算模型，采用单向板条的挠度计算公式和有限元计算结果反算式（17）中的挠度放大系数ηx，最后可得到ηx和d/lmx的拟合线性关系直线如图22所示，拟合优度R2=0.861 4。式（17）中的挠度扩大系数ηx可按下式计算：

图21 单元板条有限元计算模型Fig.21 Finite element calculation model of unit slab

图22 拟合ηx和d/lmx的线性关系直线Fig.22 Fitting a linear relationship between ηxand d/lmx

3.6 公式计算与有限元分析对比

采用单向单元板条计算结果拟合的挠度放大系数η用于计算双向板的条带法，双向板公式计算和有限元计算对比结果如表3所示，其中误差=（公式结果-有限元结果）∕有限元结果×100%。可以看出公式计算结果多数偏大，这是由于单元板条拟合挠度放大系数η时未考虑相邻板条的影响，但可以发现计算误差均在15%以内，说明相邻板条的影响不大。可知该挠度计算公式计算偏安全，同时也可满足工程设计计算的需求。