页岩抗张力学行为各向异性实验与理论研究

马天寿，王浩男，刘梦云，彭念,2，郑南鑫，易晟昊

(1.西南石油大学石油与天然气工程学院，四川成都，610500；2.西南石油大学油气藏地质及开发工程国家重点实验室，四川成都，610500；3.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，湖北武汉，430071)

近年来，由于常规油气资源的逐步枯竭，页岩气等非常规油气资源在能源供给方面发挥了十分重要的作用。水平井技术和水力压裂技术是页岩气高效开发的核心技术。由于页岩地层经受了非常特殊的沉积历史和环境，导致其具有显著的各向异性特征，表现为不同方向的力学性质和微观结构存在显著差异[1-2]，尤其是页岩抗张力学行为各向异性特征，目前还没有得到全面、统一的认识，这为页岩气高效开发带来了许多难题与挑战[3-4]。页岩抗张力学行为各向异性特性不仅是分析地应力、地层坍塌压力和地层破裂压力的基础，而且是钻井过程中井壁破裂压力分析和压裂储层改造过程中裂缝起裂与扩展的关键[5]。近年来，国内外学者对页岩力学行为各向异性开展了深入研究[6-10]，但主要集中于页岩抗压强度、弹性模量、泊松比以及脆性各向异性等方面，抗张强度作为岩石承载力及其抗变形和破坏能力的1个关键参数，人们仅开展了岩石抗张强度各向异性实验与理论的初步研究[3,11-16]。针对页岩抗张强度各向异性，WANG等[4]研究了页岩拉伸破坏的各向异性特征，并监测了破坏过程的声发射数据，结果表明声发射特性也能反映各向异性破坏行为。同年，侯鹏等[14-15]基于不同层理角度页岩巴西劈裂实验，利用高速摄像系统和声发射系统，对页岩力学特性、裂纹扩展及声发射特征的层理效应进行了研究，结果表明抗张强度最大值出现在90°，最小值则出现在30°附近。马天寿等[16]指出，不同种类页岩抗张强度各向异性指数为1.03～4.72，其中LMX页岩抗张强度在90°时最高、0°时最低，表明页岩抗张强度具有显著各向异性。ZHANG等[13]结合巴西劈裂实验和声发射探讨了页岩在不同角度下力学性质和破坏模式。为了更加准确分析和描述页岩井周裂缝起裂与扩展力学行为，有必要进一步深入开展考虑层理角度影响的页岩抗张强度各向异性特征研究。为此，本文作者以重庆彭水页岩为研究对象，综合开展页岩声波波速各向异性、页岩抗张强度和声发射各向异性实验测试，分析声波波速、抗张强度、声发射和破坏模式的各向异性特征。基于各向异性抗张强度CPA(critical plane approach)理论，研究页岩抗张强度及破坏面方向的影响因素及其变化规律。

1 不同加载角度页岩巴西劈裂实验

1.1 实验岩样

实验样品取自重庆彭水区块露头页岩，考虑到页岩遇水易发生水化损伤，采用干空气抽吸钻取方法钻取岩芯，并根据国际岩石力学学会建议标准，沿平行层理方向钻取直径×厚度为50mm×25mm的巴西圆盘样品，钻取后采用磨石机将端面磨平，试件直径误差≤0.3mm、两端平行度误差≤0.5mm，且试件两端面应垂直于轴线。该页岩为下志留系龙马溪组黑色炭质页岩，X线衍射测试结果表明，该页岩富含石英(52.68%，质量分数，下同)、黏土矿物(29.53%)、长石(13.48%)，还夹杂少量方解石(1.87%)和白云石(2.44%)。彭水区块页岩微观结构如图1所示，电镜扫描发现页岩无机和有机孔隙多为纳米级孔隙，发育一定程度的微裂隙，基质颗粒粒度较为均匀、分选度较好，这主要是页岩定向沉积环境所致，这也使得页岩表现出各向异性特征。

图1 彭水区块页岩微观结构Fig.1 Shale microstructure in Pengshui region

1.2 巴西劈裂实验

在开展巴西劈裂实验前，首先开展了波速各向异性特征测试，在试样圆盘面上标注需要测试的方向线，并标注超声波探头安装位置，如图2所示，以沿层理方向为起始角度，每间隔15°测量实验岩心的纵横波波速，波速测试采用纵横波同轴波速测试仪器进行测试，该仪器测得的波速为同一测线的波速，有效避免了传统波速测试仪器更换探头过程中产生的位置和接触测试误差。完成波速测试后，开展不同加载角度条件下的巴西劈裂实验，并采用全波形声发射仪监测声发射响应，要求加载方向与页岩层理夹角分别为0°，15°，30°，45°，60°，75°和90°，如图3所示。图3中“箭头”代表轴向力的加载方向，声发射探头安装位置与轴向力加载方向垂直，如图3中θ=0°时的“圆点”所示。为了避免样品差异对结果的影响，单个加载角度至少测试3个试件。测试后取峰值载荷计算巴西劈裂强度为

式中：σt为巴西圆盘抗张强度；P为峰值载荷；D为巴西圆盘直径；t为巴西圆盘厚度。

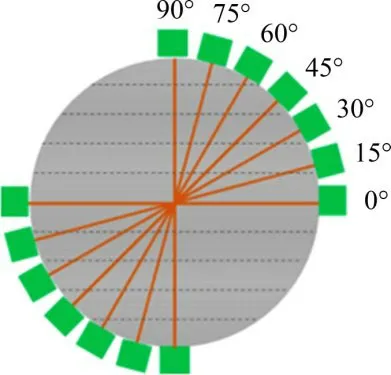
图2 页岩声波波速各向异性测试示意图Fig.2 Shaleacoustic velocity anisotropy testing schematic diagram

页岩波速和巴西劈裂实验结果如图4所示。由图4可知：整体上页岩纵横波波速随着θ的增加逐渐减小，页岩抗张强度随着θ的增加逐渐增大；不同加载角度下的页岩声发射能量和振铃计数有显著差异，加载初期的能量和振铃计数均比较小，加载中期声发射能量和振铃计数逐渐增加，加载至试件临近破坏阶段的声发射能量和振铃计数成倍增长。

2 各向异性抗张强度CPA理论

岩石抗张强度准则与岩石内部微观结构及岩石抗张强度空间分布密切相关。LEE等[17]提出一种指数形式的函数来表征横观各向同性岩石在n方向的抗张强度，其表达式为

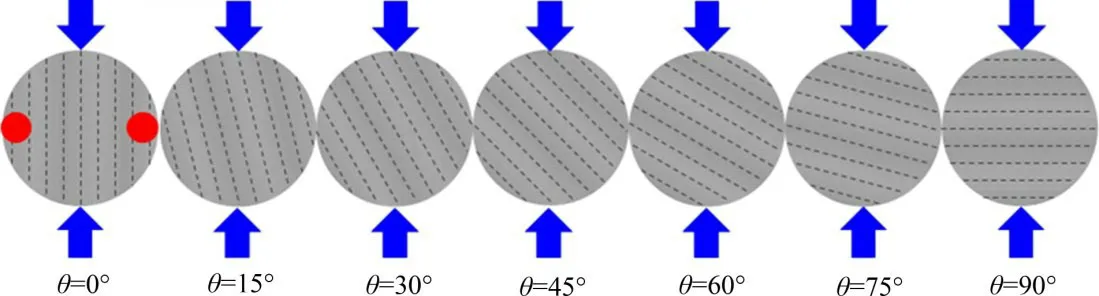
图3 页岩抗张强度和声发射各向异性测试示意图Fig.3 Shale tensile strength and acoustic emission anisotropy testing schematic diagram

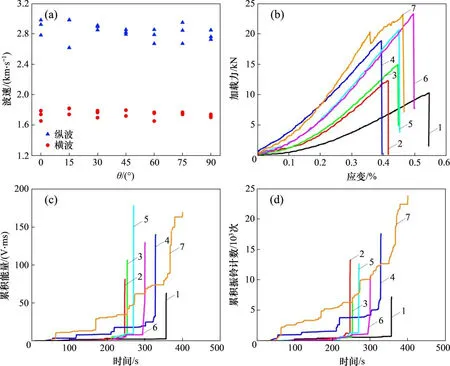
图4 不同角度下页岩各向异性测试实验结果Fig.4 Experimental results of shale anisotrophy at different angles

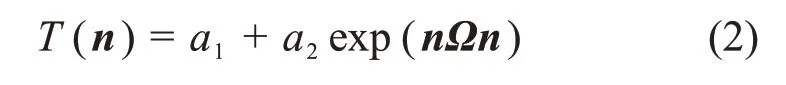
式中：T(n)为岩石在n方向的抗张强度；a1和a2为岩石强度参数；n为任意平面的法向矢量；Ω为二阶组构张量，它表示强度参数在空间分布的偏离程度。

对于横观各向同性岩石，其无迹组构张量可表示为[17]

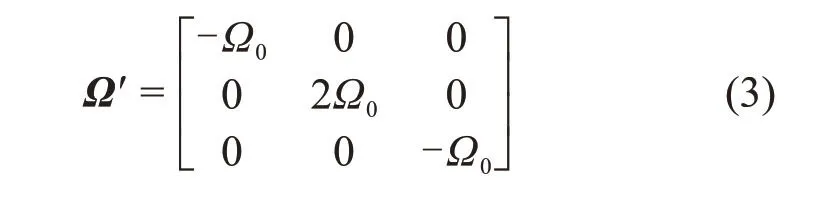
式中：Ω′为地层坐标系下岩石无迹组构张量；Ω0为强度空间分布参数。通过坐标转换，如图5所示，可将材料的无迹组构张量转到全局坐标系ei(i=1，2，3)之下：

其中：

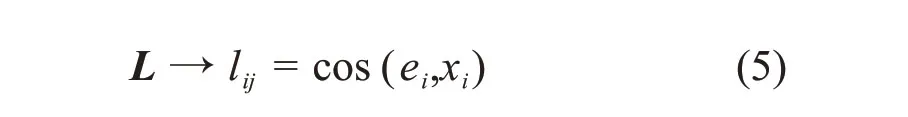
L为坐标旋转矩阵；xi为地层坐标系；ei为全局坐标系；lij为方向余弦。

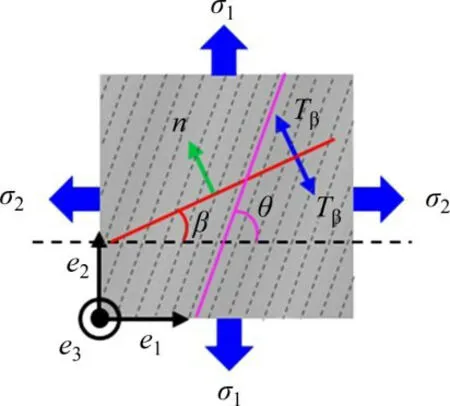
图5 二维平面的抗张受力分析示意图Fig.5 Schematic diagram of tensile mechanical analysis in two-dimensional plane

对于二维平面(见图5)，层理与基准线的夹角为θ，与基准线夹角为β方向的法向矢量可表示为

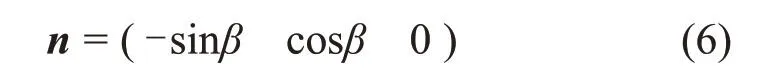
式中：β为任意给定平面夹角。

在巴西劈裂实验中，控制加载方向与层理面的夹角θ变化，因此，

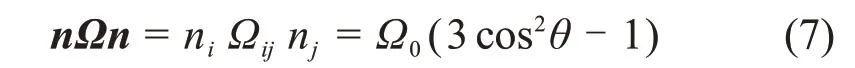
于是，将式(7)代入式(2)中可得

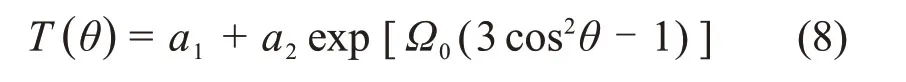
当θ分别为0°和90°时，

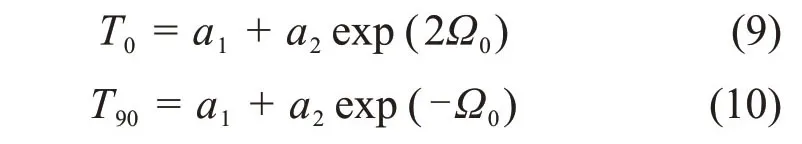
式中：T0为页岩层理面抗张强度；T90为页岩本体的抗张强度。

若T0和T90已知，则根据式(9)和式(10)可得：

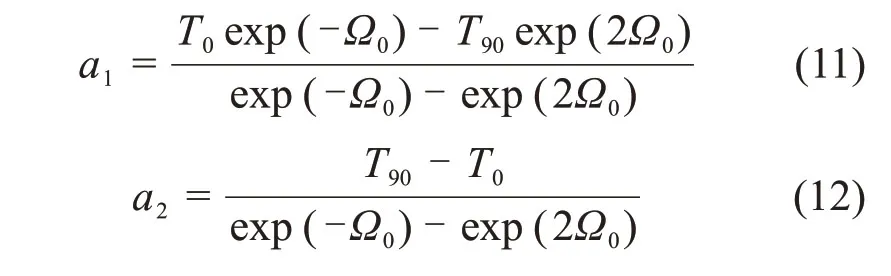
因此，将式(11)和(12)代入式(8)中，可得页岩各向异性抗张强度准则[17]：

PIETRUSZCZAK等[18]建立了一种CPA强度理论，该理论能同时获取岩石强度和破坏面方向。对于1点的应力状态，应力张量可表示为σ，对于法向矢量为n的平面，其正应力可表示为

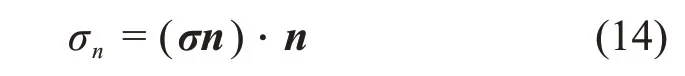
式中：σ为应力张量；σn为n方向所受拉应力。

结合式(2)和式(14)，可得到张性破坏函数：

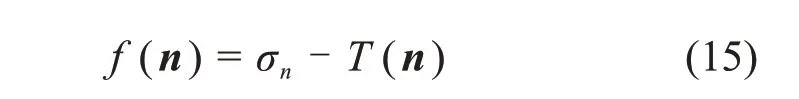
当f(n)>0时，表明法向矢量为n的平面上，其拉伸应力超过了岩石在该方向的抗张强度，岩石在该方向发生拉伸破坏，且定义该破坏面与基准线的夹角为βf。对于前面提到的CPA方法，就是寻找岩石在某一应力状态下破坏的临界平面。

3 实验结果及讨论

3.1 弹性各向异性

图6所示为不同角度下的纵横波波速测试结果。由图6可以看出：纵横波波速整体上随着θ的增加而降低，其中，在θ=0°时平均纵波波速为2 893.94m/s，在θ=90°时平均波速为2 782.06m/s，0°与90°方向的纵波波速之比为1.04；横波波速在θ=15°时最高为1 791.23m/s，在θ=90°时最低为1 718.74m/s，最大最小横波波速之比为1.04，因此，声波在页岩不同方向的纵横波传播速度差异较小，波速各向异性并不显著。

根据纵横波波速，计算不同角度下的动态弹性参数，如图7所示。从图7可以看出：弹性模量随θ的增加而降低；在θ=0°时，弹性模量最高，为19.08 GPa；在θ=90°时，弹性模量最低，为17.50 GPa。图8所示为不同页岩纵横向弹性模量和泊松比交汇图。从图8可以看出：页岩纵横向弹性模量比值主要介于1.0～2.0之间，本文彭水页岩模量各向异性差异相对较小，纵横向弹性模量比值仅为1.09。整体上看，泊松比也随着θ的增加而降低。在θ=0°时，泊松比最高，为0.26；在θ=90°时，泊松比最低，为0.16。泊松比最大最小值之比为1.625。

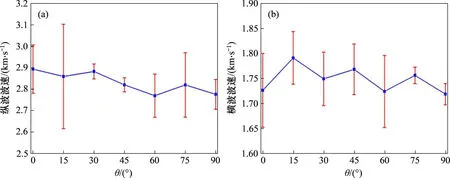
图6 不同角度下的页岩纵横波波速测试结果Fig.6 Resultsof shale longitudinal and shearwave velocity at different angles

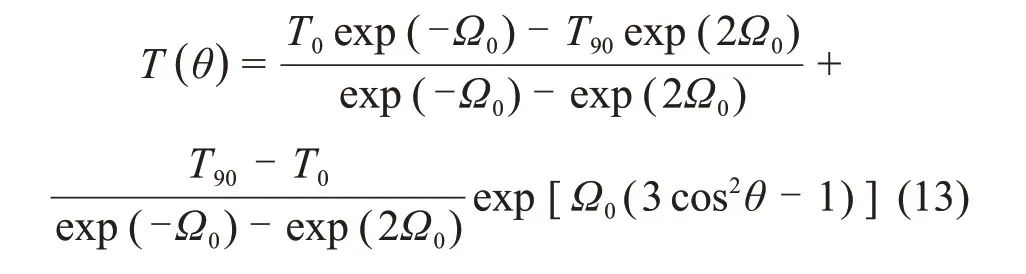
3.2 抗张强度各向异性

图9(a)所示为不同角度下的抗张强度实验结果，图9(b)所示为不同页岩纵横向抗张强度交汇图。由图9可以看出：彭水页岩抗张强度随着θ的增加而增大，θ=0°时抗张强度为5.24MPa，θ=90°时抗张强度为11.83MPa。通过页岩纵横向抗张强度交汇图可以发现，页岩普遍具有抗张强度各向异性，其纵横向抗张强度之比主要介于1.0～3.0之间，本文彭水页岩各向异性比值为2.26，说明该页岩同样具有显著的抗张强度各向异性。

通过式(13)计算了不同Ω0在不同θ下的抗张强度，对比理论值与实验值的差异，结果表明：当Ω0=0.416时，由式(13)计算的页岩抗张强度与实测结果方差最小，拟合度最高。在此基础上，运用CPA理论，获取了页岩在不同θ下的抗张强度及破裂角βf，如图10所示。从图10可以看出：CPA预测值与实验测试结果具有较好的一致性；随着θ增加，抗张强度逐渐增加，而破裂角βf先增加后降低。

3.3 声发射各向异性

图7 不同角度下的页岩弹性模量和泊松比Fig.7 Shale elastic modulus and poisson's ratio at different angles

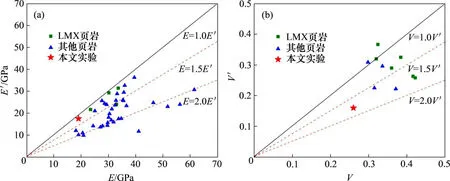
图8 页岩弹性模量和泊松比纵横向交汇图Fig.8 Intersection diagram of shaleelasticmodulus and poisson's ratio

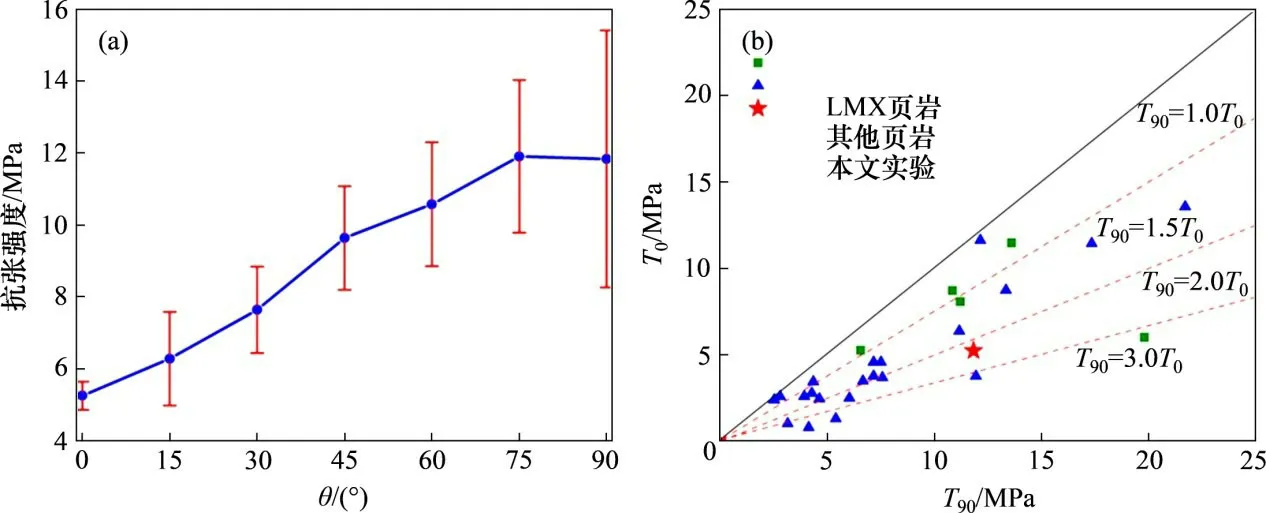
图9 不同角度下的页岩抗张强度及纵横向抗张强度交汇图Fig.9 Shale tensile strength at different angles and intersection diagram of tensile strength

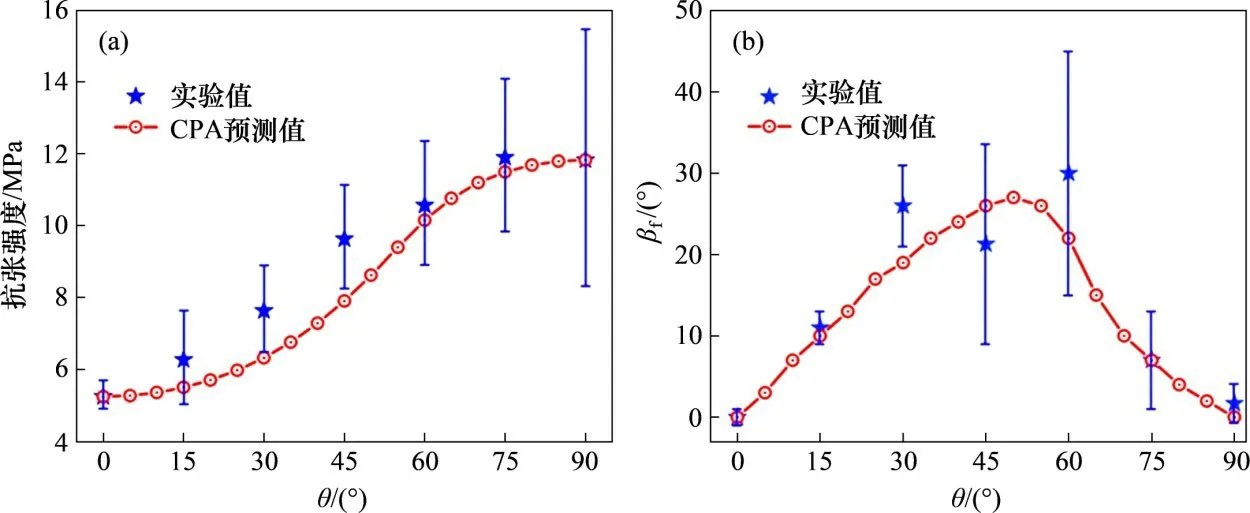
图10 不同角度下的抗张强度及破裂角Fig.10 Tensile strength and failureangleat different angles

在开展页岩抗张强度测试的过程中，同时监测了页岩由开始加载到最终试样破坏的声发射数据，获取的累计声发射能量和累计振铃计数如图11所示。图11中横坐标为各试样所承受的应力水平，代表试样所受应力状态占最终破坏应力的百分比。由图11可以看出：加载初期的声发射能量和振铃计数比较小，增长速率缓慢；在加载中后期，当应力达到80%峰值应力之后，声发射能量和振铃计数迅速增加，出现陡增形态。这说明实验前期试样内部无明显破坏，试样破坏过程主要集中在80%～100%峰值应力区间，试样内部会出现多处微小损伤或破坏，释放大量声发射能量和信号。此外，不同角度下的累计声发射能量和振铃计数差异显著，在应力状态为50%时，0°，15°，30°，45°，60°，75°和90°下的累计能量分别为1 767.85，12 620.24，4 787.66，8 426.58，4 127.68，298.05和13 000.82mV·ms，最大值出现在θ=90°，最小值出现在θ=75°，最大最小累积能量之比为43.62；0°，15°，30°，45°，60°，75°和90°下的累积振铃计数分别为479，1 293，459，1 601，513，170和3 381，最大和最小值同样出现在θ=90°和θ=75°，最大最小累积振铃计数之比为19.89。在应力状态为100%时，0°，15°，30°，45°，60°，75°和90°下的累计能量分别为62 622.38，131 444.6，106 403.4，140 165.5，178 075.9，129 579.4和163 318.3mV·ms，最大值出现在θ=90°，最小值出现在θ=0°，最大最小累积能量之比为2.61；0°，15°，30°，45°，60°，75°和90°下的累积振铃计数分别为7 230，9 883，9 732，17 656，12 700，10 592和22 479，最大和最小值分别出现在θ=90°和θ=0°，最大最小累积振铃计数之比为3.11。这些结果证实了声发射各向异性能够反映页岩的各向异性特征，但声发射各向异性与弹性模量和强度各向异性的比值差异较大。

3.4 破坏模式

图12所示为不同角度下页岩破坏形态图，图12中红色直线为加载方向，蓝色直线为试件中页岩层理方向线，绿色曲线为试样的破裂轨迹。各向异性巴西圆盘的破坏形态有3种类型：直线形、月牙形和不规则形[19]。MA等[20]将破坏模式分为5种，如图13所示，其中，“曲线1”对应穿过弱面的拉伸破坏，“曲线2”对应沿着弱面的拉伸破坏，“曲线3”对应穿过弱面的剪切破坏，“曲线4”对应沿着弱面的剪切破坏，“曲线5”对应复合破坏。由图12可以看出：试件破裂面形态有3种类型，即直线形、月牙形和不规则形；θ=0°时的巴西圆盘破裂面属于模式“2”，θ=15°时巴西圆盘破裂面属于模式“5”，θ=30°时的巴西圆盘破裂面属于模式“3”，θ=45°时的巴西圆盘破裂面属于模式“3”和“4”，θ=60°时的巴西圆盘破裂面属于模式“3”和“5”，θ=75°时的巴西圆盘破裂面属于模式“3”，θ=90°时的巴西圆盘破裂面属于模式“1”。通过以上分析可以发现：在θ由小增大的过程中，试样破坏模式先由简单到复杂，随着θ的进一步增加，试样破坏模式又由复杂变为简单。

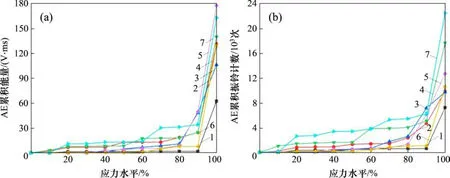
图11 不同角度下的声发射监测数据Fig.11 Acoustic emission monitoring data at differen tangles

图12 不同角度下的页岩破坏形态Fig.12 Failure morphology of shale at different angles

图13 5种典型的破坏模式[19]Fig.13 Five kindsof typical failuremodes[19]

3.5 讨论

根据第2节页岩强度空间分布函数，采用CPA理论讨论了强度空间分布参数、径向应力和强度各向异性对页岩抗张强度及破坏面方向的影响规律。

3.5.1 强度空间分布参数

图14所示为Ω0对页岩强度和破坏方向的影响。由图14可以看出：随着Ω0增加，岩石的抗张强度逐渐增大，但增长幅度逐渐减小；在Ω0较小时，随着θ增加，岩石强度逐渐增高；随着Ω0逐渐增大，岩石强度逐渐增大这一趋势将发生变化，表现为随着θ的增加，岩石强度先逐渐增高，当达到某一临界值后，随着θ增加，岩石强度近似保持恒定。Ω0对岩石拉伸破坏的方向也有显著影响，当θ较小时，βf随着Ω0的增加逐渐增大；当θ较大时，βf随着Ω0增加逐渐减小。此外，在Ω0较小时，βf变化比较平缓，如图14(b)中曲线1和2所示。随着Ω0增加，βf会由较高值突降到较小值，如图14(b)中曲线4和5所示。

3.5.2 径向应力

图15所示为不同径向应力作用下岩石抗张强度和破裂角的计算结果，由于本文考虑的是平面问题，因此径向应力只考虑了σ2，且图15中负值代表压应力，正值代表拉应力，所使用的Ω0为0.416。由图15(a)可以看出：当径向存在压应力时，岩石的抗拉强度增加，且径向压应力越大，抗拉强度越高，这主要是由于径向的压应力分量会抵消一部分轴向方向的拉应力，因此，要使岩石产生拉伸破坏，则需要更大的轴向拉力。相反地，岩石的抗拉强度随拉应力的增加逐渐减小，其原因与上述分析类似。从图15(b)可以看出：当径向应力为压应力时，随着压应力的增加，βf逐渐减小；当径向应力为拉应力时，随着拉应力的增加，βf会逐渐增大。

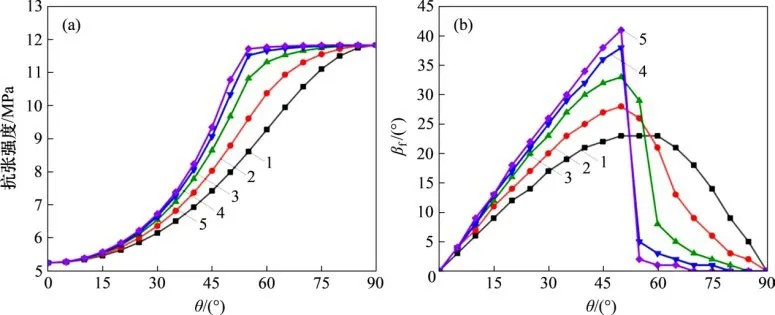
图14 不同Ω0下的抗张强度及破裂角Fig.14 Tensile strength and failure angleunder differentΩ0

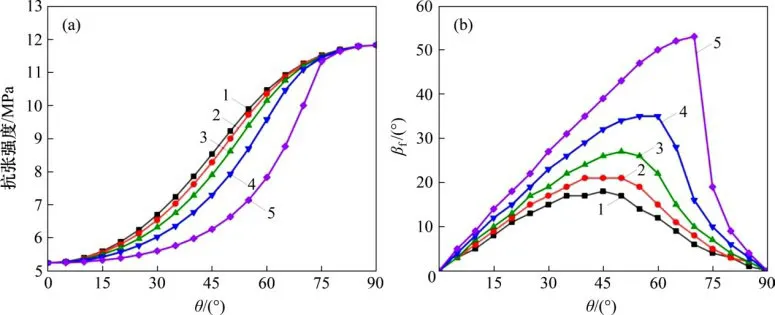
图15 不同径向应力下的抗张强度及破裂角Fig.15 Tensile strength and failure angle under different radial stresses

3.5.3 强度各向异性

为了分析强度各向异性对页岩强度和破裂角的影响，保持层理面的抗张强度不变，改变页岩本体抗张强度T90依次为10，12，14，16，18MPa，计算不同角度下的抗张强度与βf，结果如图16所示。由图16可知：随着页岩强度各向异性的增加，页岩抗张强度逐渐增加；在强度各向异性程度相同的情况下，当θ较小时，抗张强度增加不显著；随着θ增加，抗张强度增加值逐渐增大。强度各向异性对页岩破裂角也有显著影响，随着强度各向异性增加，βf逐渐增大，增长幅度随强度各向异性程度增加逐渐减小；此外，随着抗张强度各向异性增加，βf最大值由较小θ逐渐偏向较大θ。

4 结论

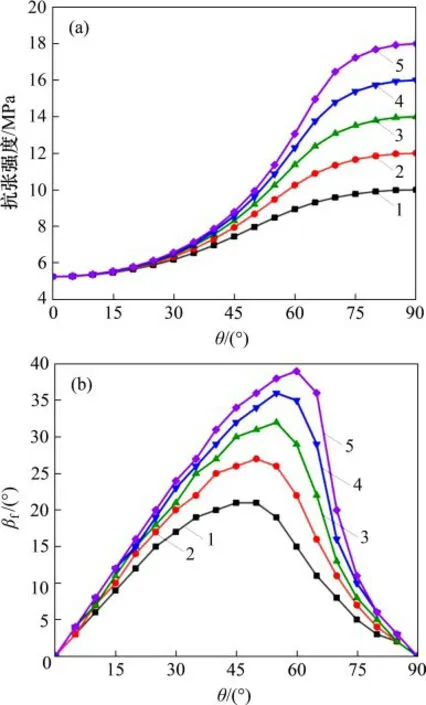
图16 各向异性条件下的抗张强度及破裂角Fig.16 Tensile strength and failure angleunder anisotropic conditions

1)整体上纵横波波速都会随θ(加载方向与页岩层理面的夹角)的增加而降低，但声波在页岩不同方向的纵横波传播速度差异较小，波速各向异性不显著。页岩具有显著的抗张强度各向异性，当θ=0°时，抗张强度为5.24MPa；当θ=90°时，抗张强度为11.83MPa，随着θ增加，抗张强度呈逐渐增加趋势。

2)页岩在不同角度下的累计声发射能量和振铃计数差异显著，在试样所受应力较小时，声发射监测数据变化不明显，随着应力水平增加，当达到80%应力状态后，声发射能量和振铃计数迅速增加，试样也是从此刻开始出现大规模破坏。在θ由小增大的过程中，试样破坏模式先由简单变为复杂，随着θ进一步增加，破坏模式又由复杂变为简单。

3)随着Ω0(表征页岩强度空间分布)的增加，页岩抗张强度将逐渐增大，但增长幅度逐渐减小。Ω0对岩石拉伸破坏的方向也有显著影响，随着Ω0增加，βf(破坏面与基准线的夹角)在θ较小时逐渐增大，在θ较大时逐渐减小。

4)当径向存在压应力时，岩石抗拉强度会增加，径向压应力越大，抗拉强度越高，且随着压应力的增加βf会逐渐减小。岩石的抗拉强度会随拉应力增加逐渐减小，且随着拉应力增加βf会逐渐增大。

5)随着页岩强度各向异性的增加，页岩抗张强度和βf逐渐增加，且增长幅度随强度各向异性程度增加逐渐减小。随着页岩强度各向异性的增加，βf最大值会由较小θ逐渐偏向较大θ。在同一强度各向异性程度下，页岩抗张强度增加值随θ增加逐渐增大。