浅谈大规模风电接入对系统功角稳定性的影响

吕颖利

浅谈大规模风电接入对系统功角稳定性的影响

吕颖利

（济源职业技术学院河南济源459000）

文章从双馈风电机组的故障期间这一角度研究不同规模大小的风电在出现不同的故障后对系统暂态功角稳定性的影响，并得出了不管是远、近距离的故障，想要对系统功角进行改善，就需要扩大对风电装机的规模，而风电规模越大则越能有效改善系统功角。但值得注意的是，风电装机的规模在达到相应的规模时，系统功角的稳定性反而不会改善，并在一定情况下会出现恶化。

大规模风电接入；双馈风电机组；系统功角暂态稳定

社会对于资源的利用不仅加快了社会发展的步伐，同时也带来了众多的问题，其中比较严重的是，对于能源资源的消耗过多出现了能源危机问题，并且在对能源资源使用过程中加剧了环境问题。其中风力发电是当前可在生能源中应用最广泛的一种新能源发电技术，具有一定的应用前景。但是随着社会发展对电网需求的增加，我国的电网规模越来越大，对于电网和电力系统的安全稳定运行存在一定的挑战。就目前实际情况而言，在我国现阶段使用广泛性最高且更具代表性的则是双馈风机，基于此，本文主要以双馈风电机组为主，分析其集中接入系统后对系统功角稳定的影响。

1 大规模风电接入对系统功角稳定性影响分析的必要性

当前社会的发展在一定程度上加强了对风电的要求，因此为了满足多方对风电的需求对大容量的风电进行了并网运行，但由于此种情况容易出现风电系统稳定性不高，加上电网自身在运行过程中具有十分复杂的特点，容易威胁电网的安全运行，且与传统的电力系统存在较大的区别。而研究大规模风电接入对系统功角稳定性的影响能够为相关电网调度部门在安排制定相应的输电计划以及针对风电场常规同步机组进行适当的调整提供有效的依据，并且能够使电力系统在安全水平下提高对输电线路的利用率，因此为了保证电力系统的安全稳定运行，满足正常的社会需求，需要大力研究大规模风电接入对系统功角稳定性的影响。

2 双馈风机接入后同步发电机功角稳定性

在接入风电机组之前首先要对不适应风电机组接入后的部分常规机组进行合理的替换，一般替换方式有两种，主要是通过同等容量的风电机组替换常规同步发电机，另外一种是利用各同步发电机组减出力运行来满足系统对风电机组出力的需求。

2.1 等容量双馈风电机组对同步电机替换的功角稳定特性

双馈风电机组的机端电压出现跌落现象主要是电力系统发生故障，并导致其内部产生多种变化，分析双馈风电机组的动态响应过程的关键问题则是钉子磁链的变化过程。一般来说，双馈风电机组中具有较大换流器电流内环带宽，则磁链的动态过程会明显小于电流环的实际响应速度。由下式可了解，双馈风电机组的大小直接影响着双馈风电机组的等效负电阻。另外，由定子和转子磁链相关方程可以看出其两者之间的空间矢量是由定子和转子中的点流量决定的，但实际上，由于定、转子空间矢量的角度差异不大，则说明在暂态情况下，双馈风电机组的功角变化保持在一定的范围内，同时其绝对值随着双馈风电机组的逐渐变大而变小，两者呈反比例的关系。双馈风电机组的功角摆开之后，其等效负电阻模值则会变小，同样也说明了双馈风电机组在能够增加同步发电机的功率，同时对功率极限角的变小也有重要的影响作用。这说明功角在暂态过程中摆开后，电磁功率在接入之前相应有所增加，另外对于同步发电机的加速能量能够在暂态过程中有一定的减少，对于功能的稳定有积极意义。

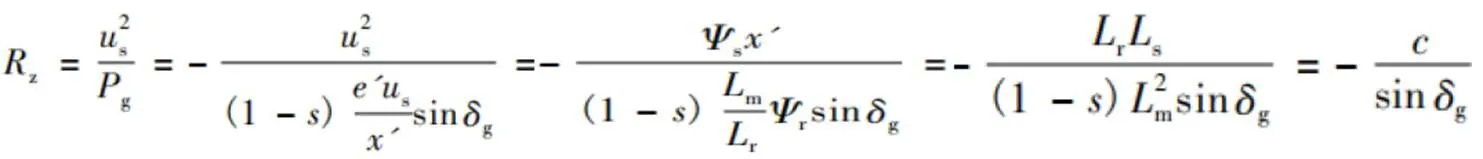
2.2 常规机组减出力运行条件下的功角稳定特性

双馈风电机组在并网之后能够分摊系统部分的有功出力，因此其机械功率在一定程度上也会同步发电机组出力的减小而减小，而当电力系统发生故障时，相较于风机并网前，各同步发电机的不平衡加速功率则会变小，而当电力系统故障恢复之后，减速功率相较于并网前则会变大，因此系统的加速面积则会变小，对于功角的恢复稳定有一定的改善作用。

3 暂态稳定分析方法研究

3.1 时域仿真法

暂态稳定分析方法主要分为两方面，一是时域仿真法，二是利用直接法进行分析，但通过对国内外文献的研究了解发现，在对暂态稳定分析时主要是通过对时域仿真法与定性分析法两者结合进行分析的。如部分相关文献采用时域仿真法进行分析发现，如果风电机组接入点存在障碍，则会影响本地区的风机甚至是影响其他地区的风机进行过电压的保护动作，会使系统暂态稳定性变高，另外系统暂态稳定性提高的另一原因则是同步机附近出现了故障，而接入风机能够对暂态稳定性加强。

3.2 直接法研究

利用直接法对暂态稳定性进行分析，主要包含两方面，一是根据暂态能量函数法对暂态稳定性进行研究，但实际上由于多种因素的影响，这一方法实际研究文献比较少，而使用扩展等面积定则法对大规模风电接入系统暂态稳定性的研究则越来越多。而对相关文献进行研究发现，若是在功率等效为临界群的机械功率中注入双馈风机，如果双馈发电机的变速发生改变，即其变速的范围变宽，并且处在故障过程中，满足这两个条件则说明有利于暂态稳定。但如果风电场在故障期间退出了运行，对于系统暂态稳定还存在一定的影响，对于这种影响进行分析时，还需要综合考量对比。

4 暂态稳定影响分析

风电如果接入后，前后功角的摇摆方向会发生一定的变化，但实际上很难判断风电在接入前后对系统功角稳定性的实际变化情况，因此有必要研究在风电接入后不会改变功角摇摆方向的情况。基于此，文章对双馈风机接入两台同步机互联简单系统的暂态稳定性进行分析，而该分析方式可以应用到多机系统中。另外结合相关文献的研究首先对Pe1和Pe2进行假设，分别假设其为0，因此可以得到以下表达式：

而对上式进行分析，若是m不小于0，则有m2与2之比小于m1与1之比，因此在故障期间，当G2的加速度明显小于1时，且0小于与0之差，则同步机功角差的摇摆方向为正向。相反，当同步机功角差的摇摆方向为反向时需要满足m小于0，而Pm2与2之比大于m1与1之比这一等式成立并在故障期间且0大于与0之差。因此可以通过m与之比研究分析功角在故障后的摇摆方向。其中各项数值代表的含义如下表所示：

表1　各项数值代表的意义

5 扩展等面积定则分析

通过扩展等面积定则可以分析出，同步发电机的加速面积与减速面积与故障持续的时间存在一定的关系，并且故障持续时间能够使同步发电机的这两方面的面积处于相等时，则故障持续时间便可转换为故障极限切除时间。而假设在系统接入风电前故障极限切除时间为Tcc，而当系统接入风电后，系统暂态稳定水平降低的原因主要是因为同步机的加速功率明显增大且减速功率减小时，而Tcc持续时，其中同步机的减速面积明显小于加速面积。相反，在接入风电后系统暂态稳定水平有一定的提高则是因为同步机的减速功率明显增加大于其加速功率减小的影响。基于此，文章将展开对同步机的稳定功角、加速功率以及减速功率在接入风电后的变化进行讨论分析，同时研究风电接入后系统暂态稳定性增加时β的范围区间。

5.1 当β小于αM且β小于1-KWP

当出现此种情况时，则说明同步机的1承担的不平衡功率的比例比较小，且小于1自身的惯量与所占系统总惯量之比。另外1同样不会大于接入风机的位置到受端的距离与送受端总距离之间的比例。根据以下两个公式可以分析出Δ大于0在故障发生后恒成立，另外w等于与Δδ之和大于0。根据等面积定则进行分析，则说明，当系统接入双反馈风电机组后，加速面积会随着稳态功角的增大而增大，减速面积则与稳态功角呈反比例变化，因此当稳态功角越大，减速面积越小，因此对于系统的暂态稳定性存在一定不利影响。

5.2 当β同时大于αM、1-KWP

出现这种情况则是同步机的1承担不平衡功率的比例相对比较大，而自身的惯量与系统总惯量之间的比例小于其承担的不平衡功率，另外，接入风机的位置到受端的距离与送受端总距离之比同样也小于1。而在故障发生后存在Δ小于0，因此如果功角在系统接入风电之后仍能正向摇摆，则大于w等于与Δ之和大于0是成立的，进而说明在接入风电之后对于系统暂态稳定是有利的。

5.3 若β小于αM而小于1-KWP

出现这种情况则说明1自身的惯量与系统总惯量的比例明显大于1承担的不平衡功率比例，而风机接入的位置到受端的距离与送受端总距离的比例小于1。而在双馈风机接入后，稳态功角相对会减小，加速面积与稳态功角呈反比例，因此加速面积会增加，但根据相关研究分析发现，若是对故障进行切除，则减速面积相应也会增加，因此不能确定双馈风机在接入后对系统暂态稳定性的影响效果。

5.4 当β同时大于αM且小于1-KWP

此种情况与上述第三种情况相反，但实际上仍然不能确定双馈风机在接入后对系统暂态稳定性的影响效果。

6 小结

本文主要是对双馈风机接入两台同步机互联简单系统的暂态稳定性进行分析，在分析过程中主要采用两种分析方式，一种是直流潮流，另一种是扩展等面积定则，具体研究结论包含两方面的内容。一是采用直流潮流对系统暂态稳定性进行分析首先是要在故障前以及对故障有效清除后的阶段，再进行分析，在分析过程中还需要双馈风机满足电压控制的方式以及双馈风机的低电压穿越特性良好。二是在双机系统中接入双馈风机后，系统暂态稳定性的变化受多种因素的影响，如同步机功角的摇摆方向，地理位置以及风电的实际渗透效果等。

[1]吴雪莲,刘福锁,李兆伟,等.基于联络线功率轨迹特征的暂态功角稳定性分析[J].中国电机工程学报,2019,39(11):3194-3200.

[2]傅旭,赵娟,张更贺,等.风电场接入对送端电网暂态特性的影响研究[J].分布式能源,2019,4(1):17-21.

[3]王爽,王毅,张祥宇.高风电渗透互联系统的功角暂态稳定分析与惯性综合控制[J].电测与仪表,2018,55(12):74-81.

吕颖利(1982- )，女，汉族，陕西西安人，硕士，讲师，研究方向：电气自动化技术、通信与信息系统。

TM614

A

2095-1205(2020)01-32-02

10.3969/j.issn.2095-1205.2020.01.20