多尺度特征融合与极限学习机结合的交通标志识别
2020-06-16马永杰程时升马芸婷
马永杰,程时升,马芸婷,陈 敏
(西北师范大学 物理与电子工程学院,甘肃 兰州 730070)
1 引 言
在智能交通系统(Intelligent traffic system,ITS)中,交通标志识别是其重要研究内容。由于交通标志识别是基于路面实况的复杂自然场景中的识别,很容易受到复杂光照、运动模糊、旋转倾斜、人为破坏、复杂环境背景干扰等条件的影响。
为了解决这些问题,大量的算法被提出。交通标志的识别主要由特征提取和分类器设计两部分组成,传统的特征提取算法主要依赖人工提取特征,如HOG特征(Histogram of Orientated Gradient)[1]、Haar特征[2]、SIFT特征(Scale-invariant feature transform)[3]、LBP特征(Local Binary Pattern)[4]等。上述算法运用人工设计的特征提取算法,提取的特征都很有限,无法得到图像深层次的特征,在分类识别上有一定的局限性。
近年来随着硬件设备的发展,深度学习算法在计算机视觉领域得到很大的发展,很多分类方法不再使用人工特征提取算法,而是将彩色图像或者灰度图像直接输入到卷积神经网络(Convolutional Neural Network, CNN)当中,通过CNN自主学习图像特征,调整参数。刘占文[5]等提出了一种基于图模型与卷积神经网络的交通标志识别,在对限速标志的识别分类中有很好的表现,取得了较好的识别效果。Zeng 等[6]使用深度神经网络和极限学习机对交通标志进行识别,用深度神经网络进行特征提取,采用极限学习机(Extreme Learning Machine,ELM)对学习到的特征进行分类识别,识别准确率有所提高,但由于仅利用了最后一层特征图,没有考虑到不同尺寸卷积核提取到的不同特征信息对分类的影响,对特征的表达能力不足。
传统CNN特征提取方法需要输入固定大小的图片,但实际上识别目标的尺寸是不相同的,且单一尺寸的卷积核容易丢失一些重要信息。在深度学习中, 多尺度信息的输入可以防止设计的卷积神经网络陷入局部最优解, 促进网络参数的更新,大量CNN研究工作及其应用都是基于多尺度方向展开的[7-10]。
Liu等[11]提出了一种抽样轮廓波变换(Non-Subsampled Contourlet Transform,NSCT)和卷积神经网络的X射线图像多尺度融合框架,通过执行NSCT对输入图像进行预处理,提取丰富的特征集合,获得图像多尺度、多方向的表示。该方法与相应的空间域方法相比具有明显优势,在该领域的未来研究中具有很大的潜力。Xiang[12]等设计了一个非对称多尺度卷积神经网络用于人蛋白图谱(Human Protein Atlas,HPA)分类,通过输入不同尺度的图像,设计了3组卷积层个数相同但卷积核大小不同的非对称卷积神经网络,该方法可以自动提取图像深度特征,实现多标签HPA识别。实验表明,相比于单一尺度,采用多尺度特征提取方法分类效果得到明显改善。Sérgio[13]提出了一种基于卷积神经网络和传统特征提取器的手部姿态识别方法,并使用二进制、灰度和深度数据以及两种不同的验证技术进行了大量的实验,实验表明基于特征融合的卷积神经网络在验证技术和图像表示的组合中表现得更好。
在交通标志的识别中,车辆行驶中所采集到的交通标志图像,由于相对位置的不断变化,图像尺寸也在不断地改变。因而本文提出了一种多尺度特征融合的CNN结构, 通过将不同尺度的图像输入到适合图像尺寸的训练网络,提取不同尺度的特征并将其进行融合为一个新的网络,最后将融合网络的全连接层进行训练,得到具有更强表达能力的特征向量,再将得到的特征向量送入ELM分类器实现交通标志识别。
2 多尺度特征融合与ELM结合的交通标志识别方法
2.1 网络主体结构
交通标志图像是自然场景中的图像,容易受到光照、形变、拍摄角度以及人为涂抹破坏的影响,对交通标志识别研究具有一定的挑战。CNN对于输入图像的平移、缩放、倾斜等形变具有较好的鲁棒性,但是CNN模型最终的识别效果会因为输入图像尺寸的改变而发生变化[14]。图像金字塔是把图像表示为一系列图像集合,并且分辨率是逐渐降低的,可用于对数据集的扩增,实际也是一种多尺度的一种体现[15]。受图像金字塔的启发,采用不同尺寸交通标志图像作为输入,可以使模型具有更强的鲁棒性。在深度学习中,多尺度的信息输入再融合,可以防止算法求解过程中陷入局部最优解,有利于网络参数的更新,并且可以获得图像更多的信息,增强模型的鲁棒性[16]。融合模型的网络参数较为庞大,ELM算法在训练时需要调整的参数小,训练时间会减少[17]。
因此,本文提出多尺度特征融合与ELM结合的交通标志识别算法,首先将交通标志图像进行预处理,增强图像的局部特征,然后将图像分为3个尺寸输入到对应的网络之中,并在3个网络中分别进行适合图像尺寸的卷积和下采样操作,将3个网络上得到的特征在全连接层进行融合,最后将融合网络得到的特征向量送入ELM分类器进行识别。为适应不用尺寸图像的特征,所设计网络的卷积核大小不同,网络深度也不同,大尺寸的卷积核通过卷积操作可以得到更加边缘和全局的特征,而小尺寸的卷积核可以得到纹理更加突出的局部特征。
多尺度卷积神经网络的算法步骤包括:
(1)对交通标志图像进行预处理,增强图像的局部特征,然后归一化为3个尺寸图像输入网络,预训练网络模型。
(2)根据输入图像尺寸大小的不同设计适合交通标志识别的卷积核尺寸和网络深度。
(3)在预训练网络模型的第一个全连接层,将3个网络生成的特征图利用串行融合的方法进行融合,再将融合后的网络进行微调,训练融合网络的全连接层。
(4)将融合网络得到的特征向量输入ELM分类器进行交通标志识别,网络结构如图1所示。
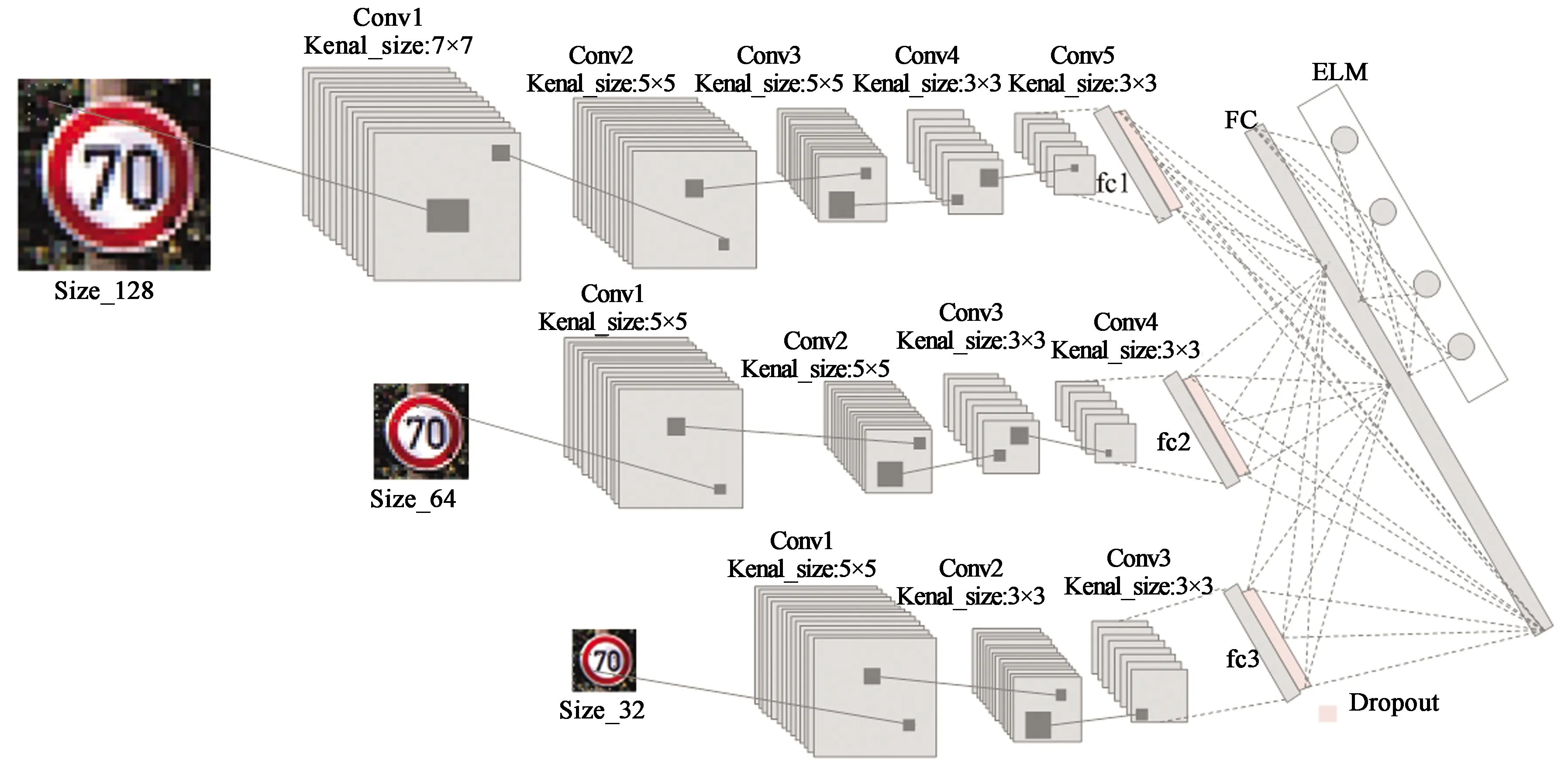
图1 多尺度卷积神经网络的结构Fig.1 Structure of multi-scale convolution neural networks
2.2 数据预处理
实验数据集采用的是2011年在神经网络国际联合会议上,波鸿大学公布的由INI-RTCV组织建立的德国交通标志数据库(GTSRB)。该数据库是车载高清摄像头在驾驶场景的视频中截取出来的,包含43类交通标志,如图2所示。其中训练集有39 029幅,测试集有12 630幅,总计为51 839幅图像。图片质量参差不齐,受到自然场景光照、图片采集角度变化、人为涂抹污染等诸多条件的影响,可以检验算法的实时性与鲁棒性。数据预处理包含数据增强和图像尺寸归一化两部分内容。

图2 GTSRB数据库的43类交通标志Fig.2 43 classes traffic signs in GTSRB dataset
2.2.1 数据增强
数据增强的目的是凸出图像的细节部分,提高图像的清晰度,直接对彩色图像进行数据增强可以保持图像更多的梯度特征,使网络提取到的特征更加全面。直方图变换增强可以避免使用灰度化之后的图像丢失图像颜色特征,因此本文选择使用直方图均衡化进行图像增强,如图3所示。

图3 原始图像与直方图均衡化对比Fig.3 Original image and histogram equalization
2.2.2 图像尺寸归一化
GTSRB数据库中图片从自然场景中采集,由于拍摄角度的变化,使交通标志图像尺寸大小参差不齐,而卷积神经网络在输入图片时需要将图像尺寸归一化,不同尺寸的图像对于网络的分类能力会有影响,考虑运算量并尽量保留更多的特征,本文选择双线性插值法对图像进行归一化处理。把图像归一化为32×32,64×64,128×128三组不同尺寸的图像作为数据集输入相应的预训练网络。
2.3 多尺度CNN特征提取
卷积神经网络主要由可见层和隐藏层组成。可见层指的是输入、输出层,隐藏层包括卷积层、下采样层和全连接层。本文算法进行多尺度融合卷积,所以应该着重考虑输入层尺寸的选择和卷积层设计,为适应不同尺寸图片的特征提取,选择不同大小的卷积核。
(1)在模型设计中,首先把图像预处理成大小不同的3种尺寸,即32×32,64×64,128×128,以不同的尺寸分别输入到3个预训练CNN之中,并且根据尺寸大小的不同设计相应的卷积层和网络深度。32×32的图像用3个卷积层进行特征提取,第一层卷积层采用5×5的卷积核,后两层采用3×3的卷积核。64×64的图像用4个卷积层进行提取特征,前2层卷积层采用5×5的卷积核,后2层采用3×3的卷积核。128×128的图像用5个卷积层提取特征,第一层卷积层采用7×7的卷积核,中间两层采用5×5的卷积核,最后两层采用3×3的卷积核。卷积层上的每个特征图都代表提取到的一组特征,并且每个特征图的每个神经元都与上一层的局部感受野相连接,实现权值共享。卷积层的计算公式为:
(1)
式中,Mj指的是所有图像特征的集合,kij是卷积核,bj是每个图像特征的偏移量。不同深度的网络对特征提取的能力不同,并且不同尺寸的卷积核所提取到的图像信息也不同,具体网络参数如表1所示。
(2)在卷积层得到特征响应图之后用ReLU激活函数进行非线性表达映射到下一层。ReLU是一种从底部进行半修正的函数,其数学公式是:
(2)
当输入x≤0时,输出为0值,当x>0 时,输出为输入值x。该函数为非饱和函数,解决了梯度消失问题。
(3)由于下采样层具有降低特征维度的作用,但是又不改变特征图的数目,并且下采样层一定程度增强了对图像位移、缩放和扭曲等形变的鲁棒性,所以在经过非线性映射之后将特征图输入下采样层。下采样操作的方式有最大池化法和平均池化法两种,如图4所示。本文选择最大池化法进行下采样操作。最大池化法是提取图像区域中最大值作为该区域池化后的值,并且在进行池化之后,网络的输出深度不变。下采样的公式为:
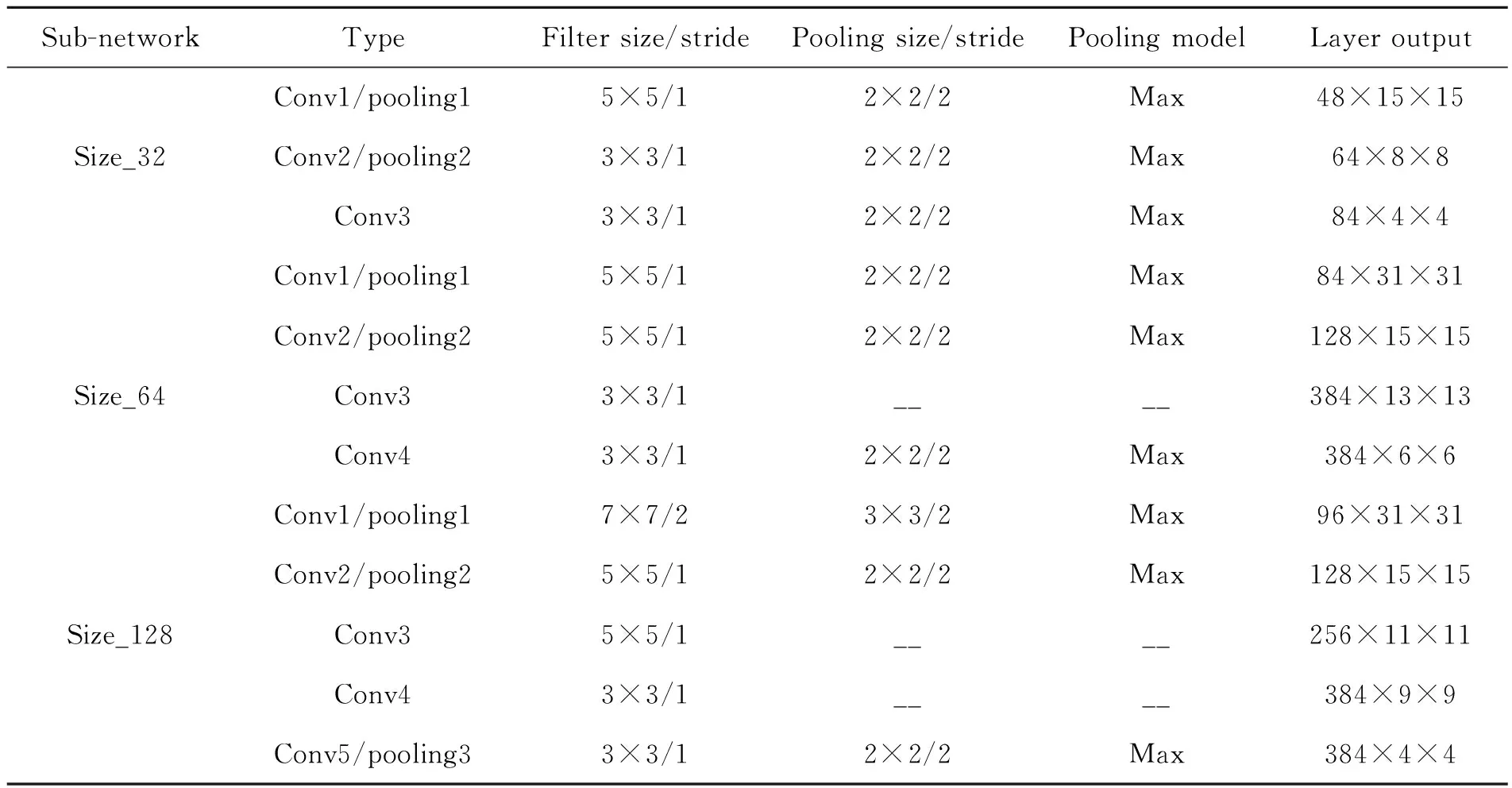
表1 多尺度卷积神经网络模型参数设置Tab.1 Parameter setting of multi-scale convolution neural network model
(3)
式中,d表示一个下采样函数,βj为权重系数,bj为偏置系数。
(4)在3个预训练网络的第一个全连接层之后添加一个dropout层,随机删除网络一部分神经元,可以降低网络的参数,并预防和降低网络的过拟合。
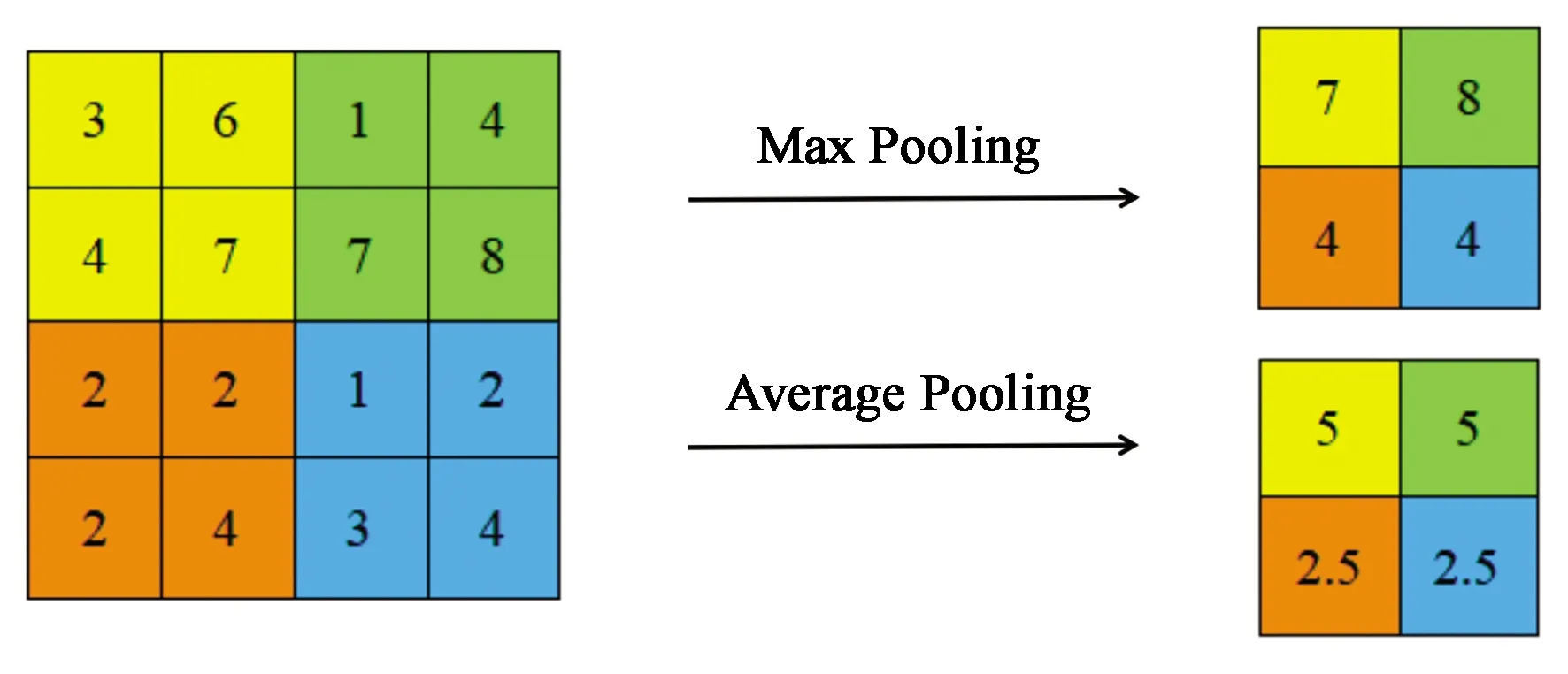
图4 最大池化和平均池化Fig.4 Max pooling and average pooling
2.4 多尺度特征融合
多尺度融合卷积神经网络的具体参数如表1所示,其中Conv表示该层只有一个卷积层,Conv/pooling表示该卷积层之后还包含一个池化层,每个卷积层之后都有一个ReLU激活函数层,多尺度特征级联方式用公式(4)实现:
(4)
式中:Fi为不同的预训练网络的全连接层的特征,n为用于特征级联的预训练CNN的个数。特征融合在3个预训练网络的第一个全连接层进行,融合的方法为特征层叠加,每两个预训练网络的全连接层之间用一个Concat层进行特征拼接,本文选择在通道上进行拼接,拼接实现方式如下:
(5)
对于两路输入来说,如果通道数相同且后面带卷积,则式中Xi和Yi分别代表两个不同网络的其中任意的一个通道,K代表卷积核,Zconcat代表单个输出通道的拼接。
(6)
式中N为特征图的数量,F1、F2、F3分别表示本文3个预训练网络的全连接层,C1、C2、C3分别代表3个预训练网络中的某一个通路,FMCNN代表在通道上进行拼接得到的全连接层的特征图,H和W分别代表特征图的高和宽。
将拼接后的特征输入到融合网络的全连接层,并微调融合网络的全连接层,最后将融合的特征送入ELM分类器进行分类。多尺度特征融合网络有很多优点,不同尺寸图像设计适合的卷积核和网络深度,大尺寸的卷积核提取图像的粗粒度特征,可以保留交通标志的轮廓特征;小尺度卷积核有助于细粒度特征的提取,局部纹理特征在特征图中也可以很好地展现。不同尺寸图像特征图的组合输入,粗粒度与细粒度的结合,提高了网络的识别精度和表达能力。
2.5 ELM分类器
通常卷积神经网络使用Softmax分类器对图像进行分类,在易混淆的图像中表现不佳。多尺度特征融合网络参数较大,特征向量维度高于单一尺度特征。考虑到模型的高效性,需要选择一种计算量小、训练时间短、满足模型高效性的分类器。ELM是一种新型的快速学习算法,对于单隐层神经网络,ELM可以随机初始化输入权重和偏置并得到相应的输出权重,不需要重复调整权值和阈值,降低了计算复杂度,训练时间更快,保证了模型的高效性,其结构如图5所示。

图5 ELM分类器结构Fig.5 ELM classifier structure
由图5可以看出,ELM由输入层、隐含层、输出层3层组成,其中输入x为多尺度特征融合网络得到的特征向量,d为输入的维度(x∈Rd,x=(x1,...,xd)T),特征向量x在隐层被映射为向量 (G(a1,b1,x),…,G(aL,bL,x))T。其中G(ai,bi,x)是第i个加性隐节点的输出, 其计算公式如下:
G(ai,bi,x)=g(ai·x+bi),
ai∈Rd,bi∈R,
(7)
式中:g为激活函数,ai表示第i个隐形节点与所有输入节点之间的权重,bi表示偏置,i=1,2,…L。输入的交通标志特征向量在隐层经过线性变换后,输出一个m维的向量f(x),其公式如下,m相当于交通标志识别的43个类别。
(8)
ELM的训练集合为{(xj,tj)|xj∈Rd,tj∈Rm,j=1,…,N},式中xj为融合网络输出的多尺度交通标志特征向量,tj为xj的标签,在对ELM分类器进行训练时,每个交通标志的特征向量xj传入ELM分类器中,tj为期待输出结果,并且每个标签向量tj都有一个特征向量xj对应。对于回归分类算法,标签tj直接代表了模型对于输入向量xj的响应,随机初始化输入权重和偏置(ai,bi,i=1,…,L),并得到相应的输出权重, 隐含层和输出层之间的连接权值(βi,…,βL)不需要迭代调整,而是通过解方程组一次性确定,公式如下:
Hβ=T,
(9)
其中H和β分别为:
(10)
式中:H是隐层节点的输出,β为输出权重,T为期望输出。
β*的最小二乘解可以利用MP广义逆解析得到,并且具有最小范数:
β*=H†T,
(11)
其中,H†是矩阵H的Moore-Penrose广义逆。最终可以得到ELM的输出方程:
f(x)=β*Th(x),
(12)
综上所述,ELM的训练与测试过程如图6所示。
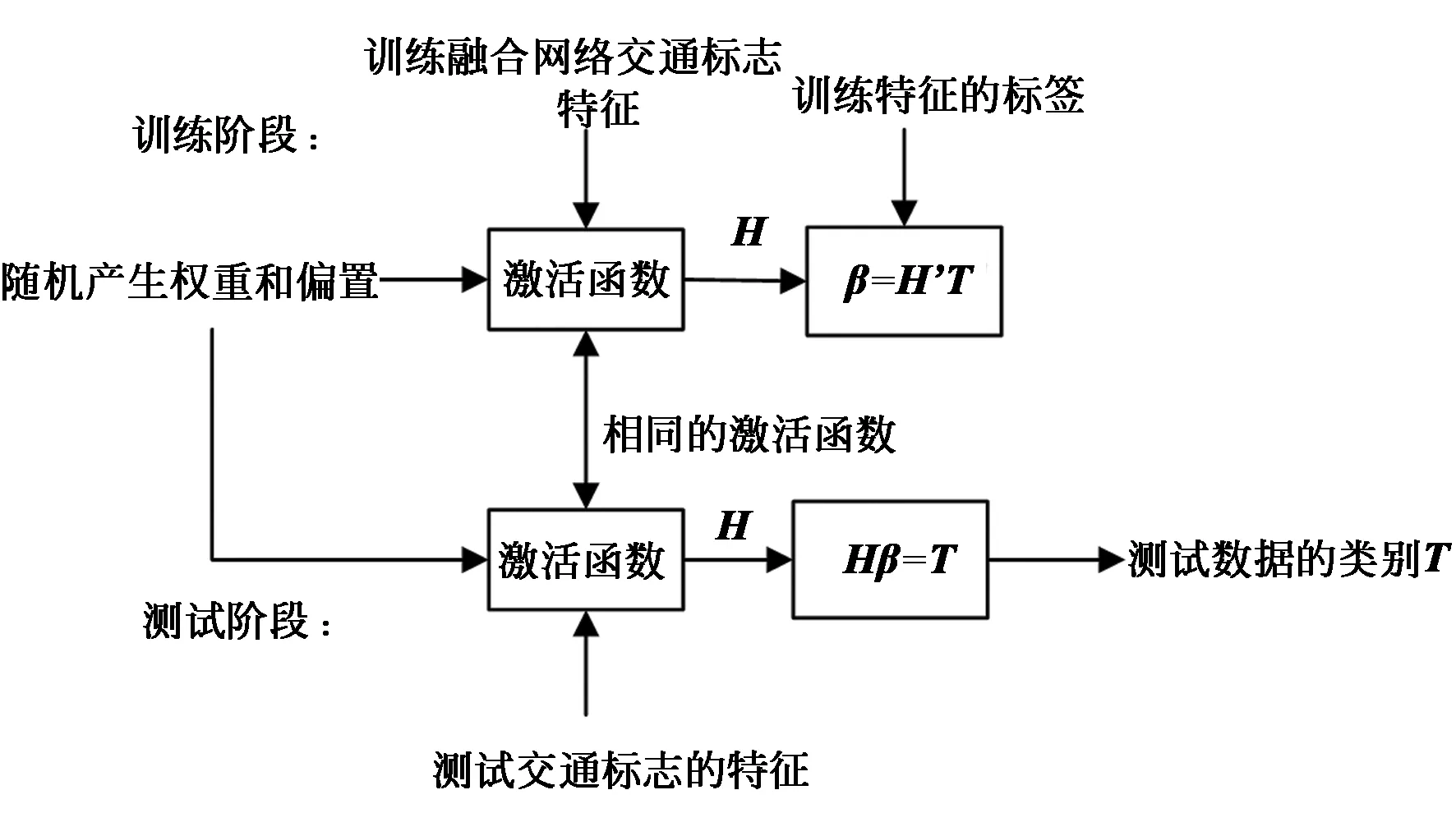
图6 ELM的训练与测试过程Fig.6 ELM training and testing process
3 实验结果与分析
3.1 实验方案
(1)将不同尺寸图像输入网络进行预训练,画出各个预训练网络的训练曲线,确保该预训练网络的合理性,并可用于模型融合。
(2)多尺度特征级联。将预训练好的3个网络的全连接层进行特征级联,并进行比选实验,设计不同的特征级联方式,选择出分类性能最好的一组。
(3)将得到的特征向量分别输入到支持向量机,Softmax分类器中进行分类识别,并与本文使用的ELM分类器进行对比。
(4)针对GTSRB数据集,采用不同的算法和本文算法进行分类,比较总体分类精度和分类时间,评估算法性能的优劣。
3.2 实验环境
实验所用的计算机配置是I5-7500处理器, 3.4 GHz主频, 16 GB内存,Nvidia GeForceGT730显卡,Ubuntu 16.04版本的Linux 操作系统,深度学习框架为Caffe[18],软件编程环境为Python 2.7。
在实验设施配置差别不大、识别速度相近的情况下,识别准确率KAcc作为评价算法性能的主要指标:
(13)
式中:ni代表识别正确的样本,N代表测试的样本总量。
3.3 实验结果及分析
3.3.1 网络模型的预训练
用德国交通标志数据库(GTSRB)对3个网络进行预训练,3个网络均使用随机梯度下降算法进行参数更新,训练网络模型的参数配置相同,基础学习率为0.01,防止过拟合的权重衰减项为0.000 5,学习率变化因子为0.1,最大迭代次数为10 000,学习率调整策略为step,调整策略参数step_size设置为3 000,进行3次学习率的调整,通过训练损失值和测试损失值来判断预训练的网络是否存在过拟合现象,以保证融合模型的精度。图7显示了4个模型的分类精度、训练损失值和测试损失值变化曲线,其中图7(a)为输入图片尺寸为32×32的网络性能曲线,图7(b)为输入图片尺寸为64×64的网络性能曲线,图7(c)为输入图片尺寸为128×128的网络性能曲线,7(d)为融合模型的网络性能曲线。
由图7可以看出,预训练模型随着迭代次数的不断增加,分类精度都是先快速增长,再逐渐趋于平稳,表明预训练的模型有较好的泛化能力,可用于模型的融合。损失值也是在前几次迭代过程中快速降低之后再趋于平稳,最终基本保持不变,表明模型的学习能力逐渐下降,分类精度提升趋于平稳。融合后的模型,测试损失值的下降速度虽然不如预训练模型,但是分类精度更高,达到99.32%后逐渐趋于平稳。
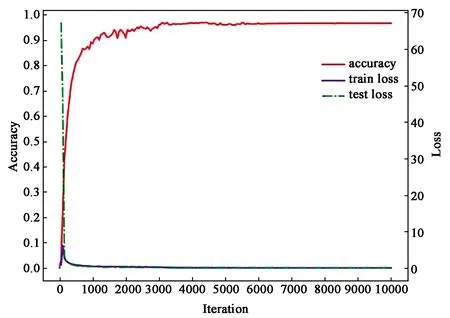
(a)Size_32
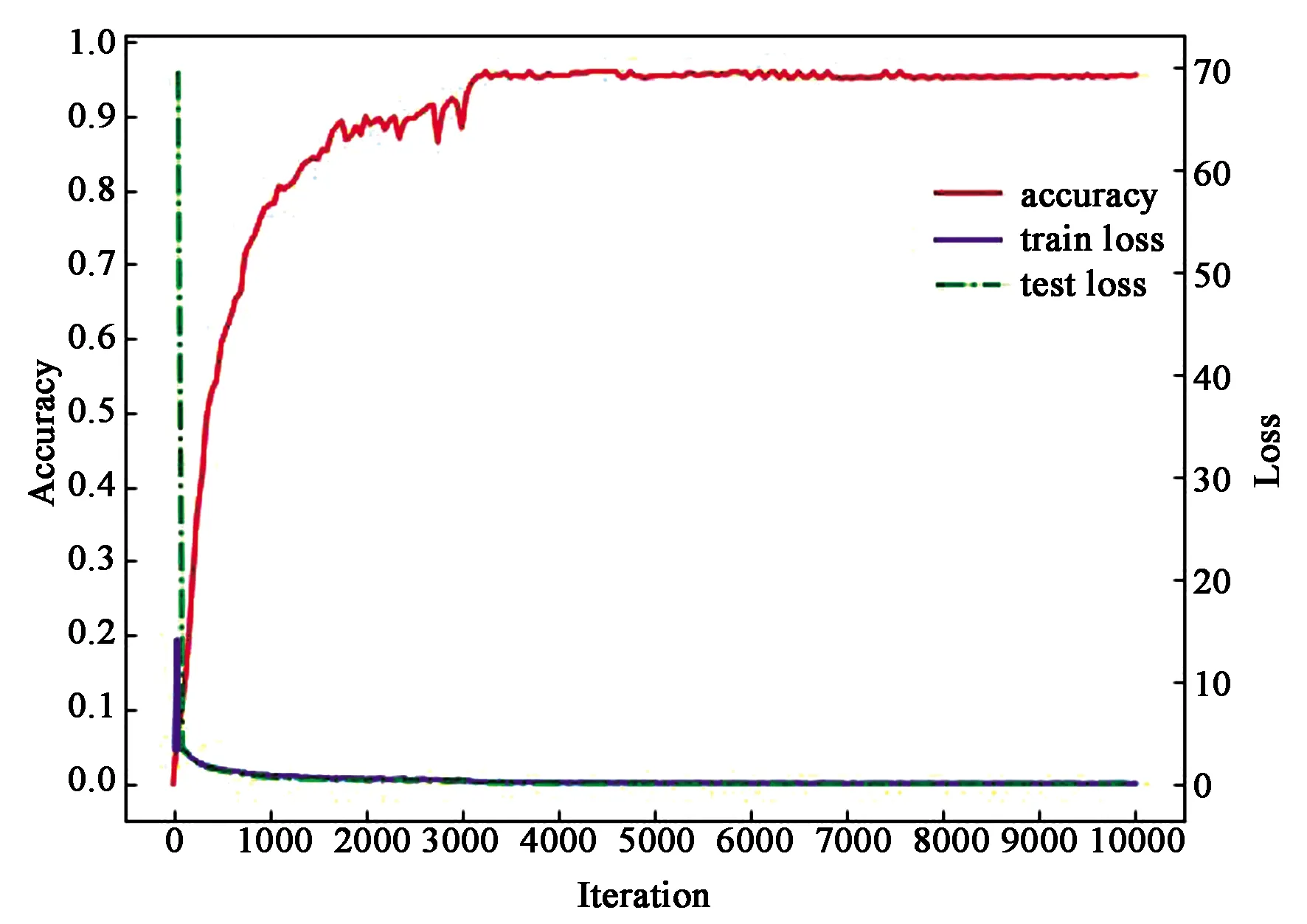
(b) Size_64

(c)Size_128
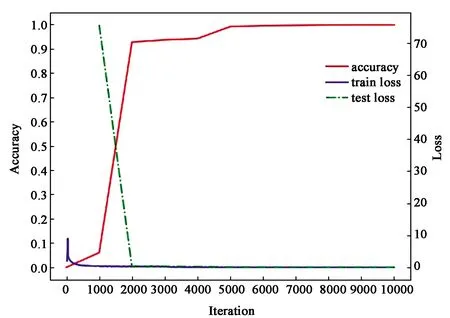
(d) Multi-scale图7 损失值和分类精度Fig.7 Cross entropy loss and classification accuracy
3.3.2 特征级联
由上文所述的级联公式(4),将网络进行级联,根据级联CNN的数量分为二网络级联和三网络级联,再将级联网络的全连接层进行二次训练。表2为不同级联方法分类结果。
从表中可以看出,在单独的网络中输入尺寸为32×32的图像时识别精度较高,这是因为该交通标志数据集的图像分辨率在15×15到222×193像素。统计结果显示,像素值大小的中位数为41×40,所以网络在该尺寸的识别率较高。融合的网络相对于单一网络分类的准确率都有所提高,表明不同网络之间的相互组合可以提高识别精度。
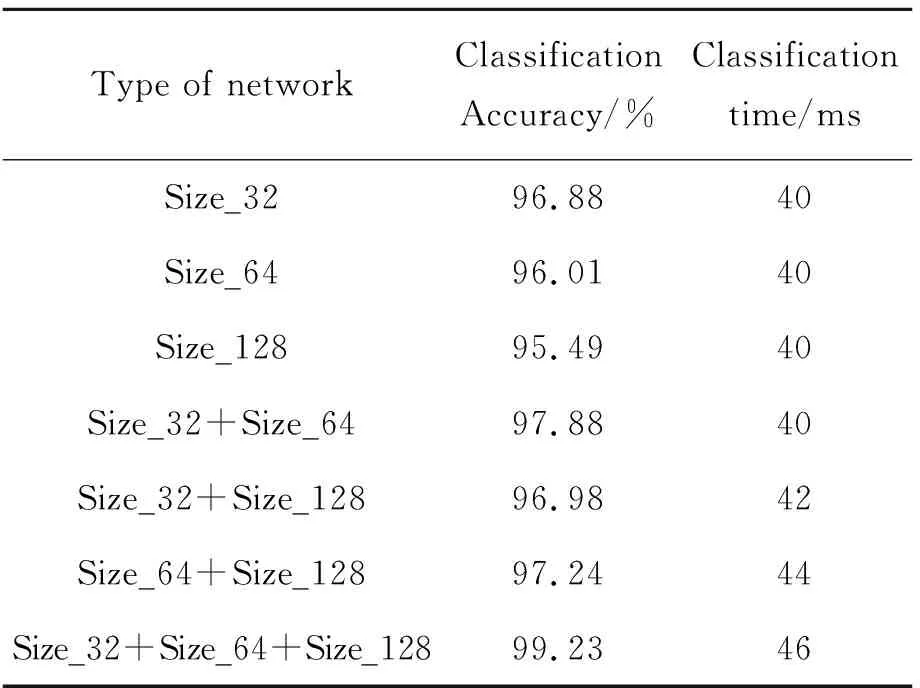
表2 不同级联方法分类结果Tab.2 Classification results of different cascading method
3.3.3 与其他分类器的对比
为了验证本文所示用的分类器的优势,设计了对比实验,将融合后得到的特征向量,分别输入到SVM分类器和Softmax分类器中,与本文ELM分类器从分类精度和分类时间两个方面进行对比,实验结果如表3所示。
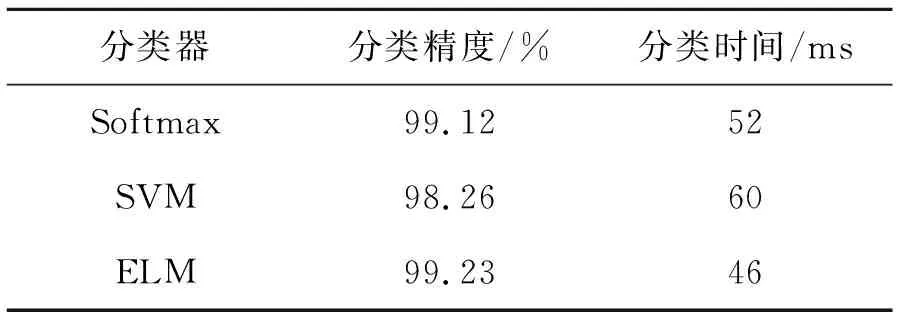
表3 不同分类器性能比较Tab.3 Performance comparison of different classifiers
从表3可以看出,ELM分类器的分类精度相较于SVM和Softmax分类器有所提高。这是由于ELM模型具有较低的复杂度,在相同时间内可处理更多的数据,增强了模型的泛化能力。此外,由于ELM分类器输入层和隐含层之间的参数采用随机初始化,且之后无需再进行调整,因此,ELM分类器学习速度更快,使得ELM分类器具有更快的分类速度。
3.3.4 与其他分类算法的对比
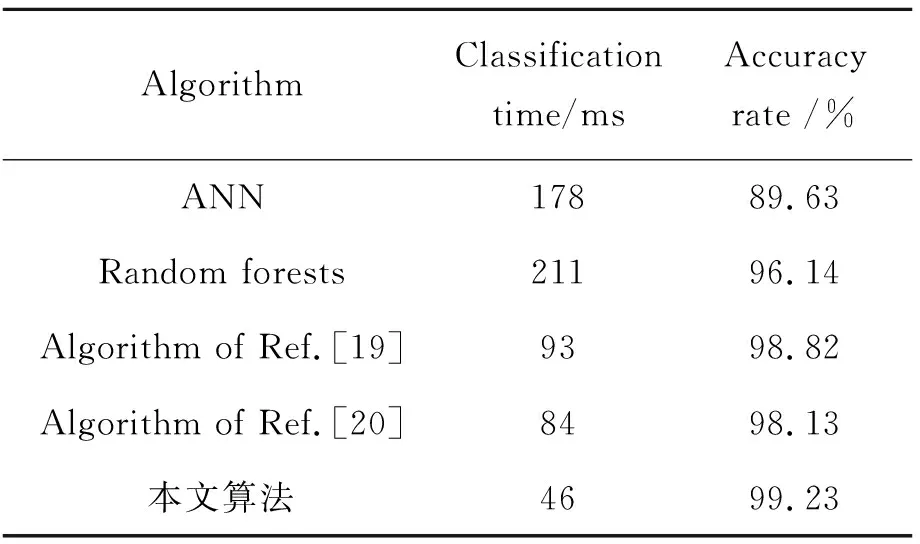
由表4可知,本文模型相对于ANN和Random forests两种算法的识别精度都有一定提高,并且分类时间都大幅度下降。相对于文献[19]和文献[20],分类精度提升不多,但是在分类时间上仍然具有一定优势。
表4 不同方法在GTSRB数据集识别结果对比
Tab.4 Comparison of different methods in GTSRB dataset recognition results
AlgorithmClassificationtime/msAccuracyrate /%ANN17889.63Random forests21196.14Algorithm of Ref.[19]9398.82Algorithm of Ref.[20]8498.13本文算法4699.23
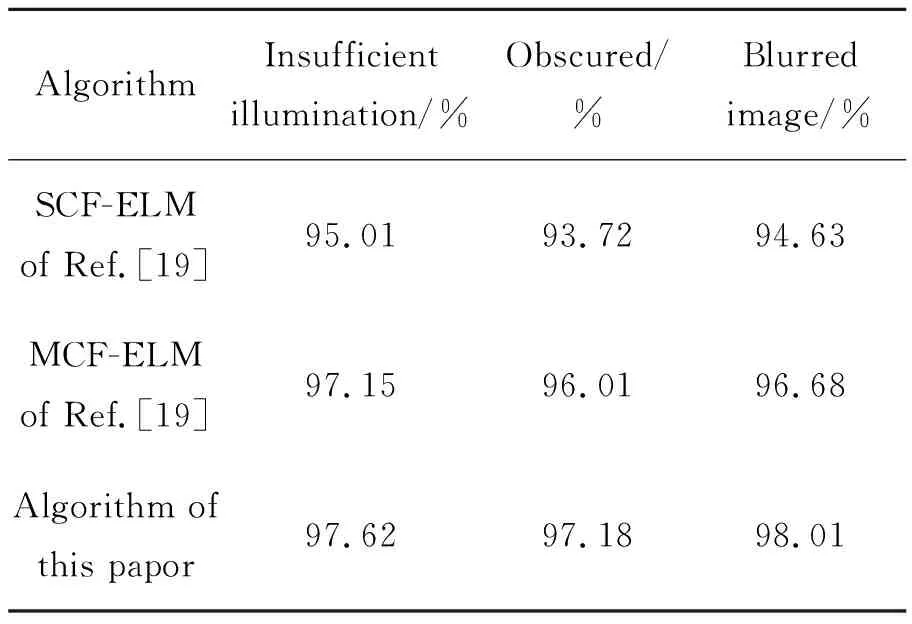
文献[19]为验证算法的鲁棒性和在复杂环境下的分类性能,在原测试集中选取了光照不足、受到遮挡和图像模糊的图像各30幅组成新的测试集,并且在单层特征和多层特征下对新的测试集进行了验证。本文用相同的方法选取测试集对算法进行验证,并且对新的测试集不进行图像增强处理,与文献[19]的对比,结果如表5所示。
表5 复杂环境下识别分类精度对比
Tab.5 Comparison of recognition classification accuracy in complex environment
AlgorithmInsufficientillumination/%Obscured/%Blurredimage/%SCF-ELMof Ref.[19] 95.0193.7294.63MCF-ELMof Ref.[19] 97.1596.0196.68Algorithm ofthis papor97.6297.1898.01
与表4中本文算法的分类准确率相比,在数据集都是复杂环境下的图像时,分类精度有所下降(表5),并且在受到遮挡的条件下精度下降较为明显,但是在整体情况下相对于文献[19]中的单层特征提取和多层特征提取算法都有所提升,特别在图像模糊的条件下提升较为明显。
本文采用多尺度图像输入,间接地增加了数据集的数量,并使用不同的3个网络对不同尺寸的图像进行预训练,卷积核大小也是根据数据集输入图片大小所设计,最后在融合网络进行分类。多尺度的信息输入再融合,可以防止算法求解过程中陷入局部最优解,有利于网络参数的更新,并且可以获得图像更多的信息,增强模型的鲁棒性[16,21-23]。在交通标志图像受环境影响较大时,特别是对于拍摄形变造成模糊的图像,本文设计的多尺度卷积融合网络在复杂环境下的鲁棒性相比于文献[19]中的多层特征融合更加优越。
表6为本文算法与其他多尺度CNN方法和单一尺度CNN算法的性能对比结果。文献[20]采用的多尺度交通标志识别方法是将每一个池化层的输出都施加到后端全连接层,再利用ELM分类器进行分类。
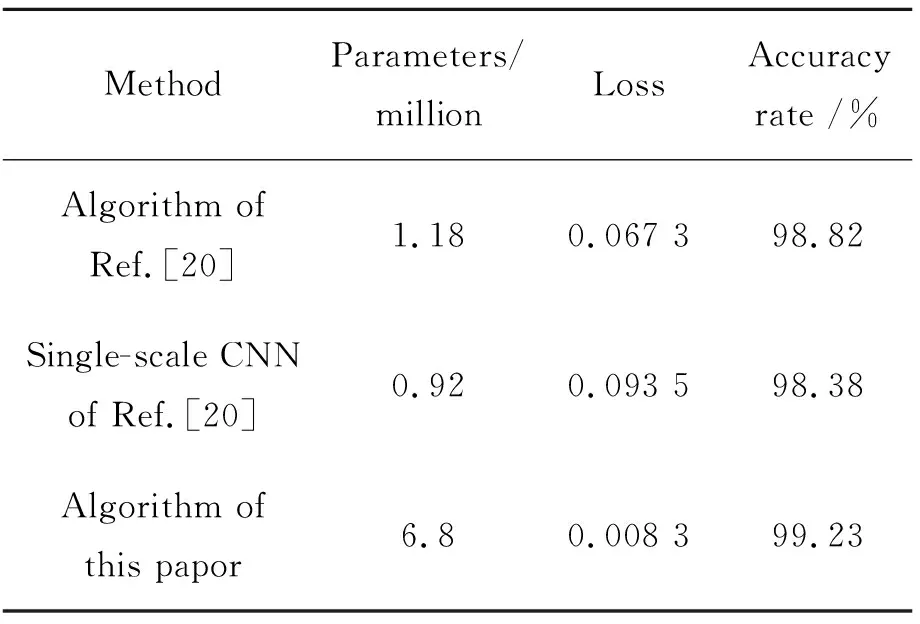
表6 与其他多尺度方法的对比Tab.6 Comparison with other multi-scale methods
从表6可以看出,由于本文使用3个预训练网络进行融合,所以参数规模要比文献[20]中的多尺度方法和单一尺度方法大,但是本文算法的损失值要远比文献[20]中的方法小很多,说明本文的多尺度融合模型的泛化能力和交通标志的特征表达能力要优于文献[20]中的多尺度模型,并且在准确率上也高出0.41%。
本文设计的多尺度卷积融合算法相对于文献[20]中的多尺度方法可以得到更高的准确率和网络模型的泛化能力,原因在于:
(1)在输入上使用3种不同尺寸图像,CNN模型最终的识别效果会因为输入图像尺寸的改变而发生变化[14],相对于文献[20]中把图片归一化成为32×32尺寸的输入,多尺度信息的输入可以增强模型的性能。
(2)在卷积层的设计上,文献[20]设计了3层卷积,并且每个卷积核的大小都是5×5。本文所设计网络的卷积核大小不同,每个预训练网络深度也不同。大尺寸的卷积核提取图像的粗粒度特征,可以保留交通标志的轮廓特征。小尺度卷积核有助于细粒度特征的提取,可以提取交通标志的局部纹理特征。不同尺寸图像特征图的组合输入,粗粒度与细粒度的结合,相比于单个网络的多尺度提取特征,融合网络多尺度的性能更好。
(3)在网络设计上,本文虽然是由3个预训练网络模型组合得到最后的特征图,但最终识别是在融合网络上完成,并且在融合网络的全连接层进行二次训练,再输入ELM分类器进行分类。相比于每一个池化层的输出都施加到后端全连接层,再利用Softmax分类器进行分类,本文得到的特征图数目更多,信息也更全面,并且选择ELM作为分类器对于分类精度的提高也起到了一定作用。
因此,本文多尺度特征融合与ELM结合的算法相较于文献[20]性能有一定的提升。
4 结 论
交通标志识别是智能交通系统的重要组成部分,自然场景中的交通标志受环境影响较为复杂,采集到的交通标志尺寸大小也是多样化的,因此本文提出一种多尺度特征融合与ELM结合的交通标志识别方法。将单一尺度的图像经过图像增强,使图像细节特征更加明显,再分别将尺寸归一化成3种不同的尺寸,然后构建适应图像尺寸的3个网络进行预训练,最后将3个网络中学习到的特征进行融合,对融合网络模型进行微调,将融合模型得到的多尺度特征输入ELM分类器进行分类。图像提取到的特征更加全面,分类识别的准确率大幅提升。实验通过在GTSRB交通标志数据集上进行实验,识别率达到了99.23%。
