空间光调制器用于多光束二维偏转的算法研究

杨飞跃，黄子强，彭逸葳

(电子科技大学 电子科学技术研究院，四川 成都 611731)

1 引 言

近年来，随着雷达目标检测与跟踪技术、空间光通信技术、航天技术等领域的快速发展，对多光束偏转技术方面的要求逐渐增高[1-2]。传统的激光雷达采用万向节等机械式扫描器件，这种器件结构繁琐，体积和重量都很大，响应时间长，使系统的性能受到了限制。近年发展的液晶光栅本质上是以大量的一维排列的光学移相器分别对光的相位进行调制的非机械式调制器件[3]。这种器件的主要优点是能够对激光实现可编程的快速、高精度的光束偏转，液晶光学移相器的重量轻、消耗功耗小，是新型的分束、偏转控制器件。然而，目前对于液晶光束控制的研究仅局限于一维标量衍射理论的计算，这种计算只考虑了一维衍射的问题，单个光学移相器无法实现光束的二维偏转。为了实现二维偏转，必须用两个一维的光学移相器对x、y方向分别作相位分布的计算、控制[4-5]。即使如此，多光束的分束偏转仍然会有镜像光束而无法应用于激光通信上。

近年来基于液晶有源矩阵的空间光调制器(AMLC-SLM)的应用，使光束的整形获得了进展[6]，通过将平行光束整形为分布在多个不同角度的光斑，为光束的直接二维偏转应用提供了可能。然而，有源矩阵中的单元数量有限，导致空间光调制器的有效面积与单元尺寸的要求相矛盾。此外，薄膜晶体管的尺寸较大，从而相位分布的周期大，也造成了光束偏转角度小和相位单元的开口率低下，像素的矩阵结构还会造成严重的黑栅效应。此外，AMLC-SLM在较高功率激光入射时，像元遮挡层、像元之间的黑色矩阵的光吸收热效应还会使AMLC-SLM中的薄膜晶体管温度升高，造成相位分布的不可忽略的偏移，严重时还可能损毁SLM。

光寻址空间光调制器(Optical Addressed SLM，OASLM)的相位分布是二维分布的，与写入光的强度分布相关[7]，所以只需单片器件就能够实现光束的分束、偏转。由于相位分布没有像素矩阵的限制，所以没有黑栅效应。OASLM的分辨率只受到液晶层厚度的限制，理论上能实现较大的偏转角度。OASLM有效孔径只与基片材料的尺寸有关，与AMLC-SLM相比有很多优点，值得认真研究。

本文探讨使用紫外光寻址的LCSLM对垂直入射的激光光束实现分束、二维偏转，研究LCSLM的相位分布对分束比、偏转角度与衍射效率的关系。

作为本文的研究基础，参考了一维液晶相控阵的部分孔径法[8]在单方向上的光束分束、偏转的方法，将其扩展至二维作为计算LCSLM诸单元相位分布的起始值。克服了光束发散角与部分孔径的大小成反比、各波束无法利用全部阵元的相位特性而使有效口径降低、衍射效率较低的缺点。

本文报告了改进的G-S(Gerchberg & Saxton)优化迭代算法[9]，按照光束整形的思路，以在像面干涉而生成多光束束斑为目标函数，确定焦平面上透明模版的相位分布的分析过程和模拟结果。该方案的特点在于通过确定OASLM上DOE(Diffraction Optical Element)面适当的二维相位分布，以高斯平行光束通过DOE以后重构波阵面，生成多个强度受控、角度受控的束斑，以此实现平行入射的光束在二维任意角度的分束和偏转。

模拟结果表明，改进的G-S算法所获DOE相位分布，经过OASLM重构波阵面，实现了光束向任意角度偏转的可编程控制，且光束的衍射效率对比部分孔径法和朴素G-S算法有明显提高，生成光束相比目标光束其均方根误差也有明显改善。

2 激光光束偏转的二维标量仿真

2.1 光寻址液晶空间光调制的系统结构

反射式OASLM器件[10]结构如图1所示，其主要功能材料包括对蓝紫光敏感的材料硅酸铋(Bi12SiO12，BSO)、氧化铟锡(ITO)透明电极、液晶层、介质反射镜。

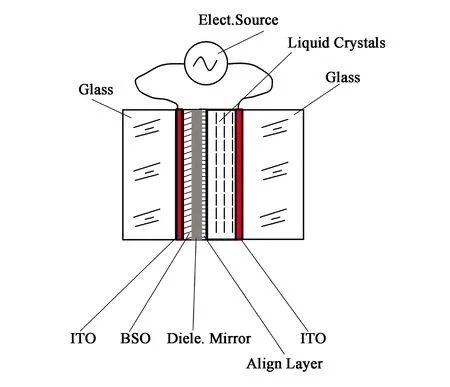
图1 反射式OASLM的结构Fig.1 Structure of reflective OASLM

图2 常温下BSO晶体的能带图Fig.2 Energy band diagram for BSO

其中BSO单晶属于立方晶系，是一种优良的光功能材料，具有良好的光电导效应，同时分子之间具有非常高的对称性。BSO材料的能带结构图如图2所示，由图可以得出BSO材料的禁带宽度为3.25 eV，由于BSO材料对蓝紫外光的激励下电阻率会急剧减小，因此当写入光的波长λ≤380 nm时，根据能带理论，使得存储在价带中的电子将会被激励到导带中，形成自由电子，此时在外电场的作用下，自由电子将会产生定向迁移形成电流。

图3展示了BSO晶体在不同波长激励下的响应，取入射光分别为绿光、蓝光和紫光，对应的波长分别为530，475，384 nm。由图可以得出不同的光波长激励下的BSO材料的光电导率不同，当由波长为384 nm的紫光激励时产生的光电导率最高，由波长为530 nm的绿光激励时最低，由此可以得出，写入光的光波长越小，光电导效率越明显。

图3 BSO晶体在不同波长激励下的响应Fig. 3 Response of BSO with different wave-lengths illumination

综上所述，本文采用紫外光作为寻址光照射到反射式OASLM上，BSO晶体在紫外光的激励下，随着光功率的增大电阻率成倍降低[11]，所以紫外光的强度分布在BSO上转换成电阻率分布，与液晶层分压后呈电压分布，最终引起液晶层与紫外光强度相对应的折射率分布，从而对介质反射镜另一侧入射的读出光(红外光)的相位进行调制。

在反射式OASLM中，功率极强的读出红外光与紫外光被介质镜隔离，可防止红外光通过倍频而影响到紫外光在BSO上的寻址，终使液晶层的折射率分布不至于受到读出光的干扰。

2.2 二维标量计算方法

为方便计算，将OASLM离散化为N×N个像素单元组成，N的大小与液晶层的厚度、BSO的厚度有关。任一像素对应区域的BSO以紫外光照射可以改变其电阻率，通过分压后改变像素液晶的偏转角度而调制其相位延迟量。

设单个像素尺寸为w×w，则透过率函数可以表示为[12]：

(1)

其中：m为像素所在位置的行坐标，x=m×w；n为像素所在位置的纵坐标，y=n×w。从而可得出像素单元所组成的纯相位液晶空间光调制的透过率函数。

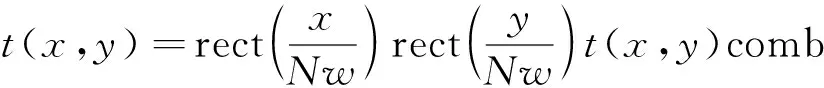
(2)

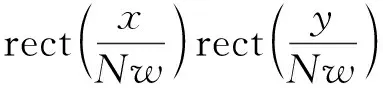
(3)

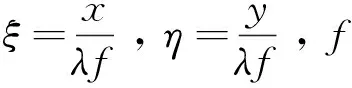
(4)

tD(m,n)=eiφ(m,n)，设入射光束的复振幅分布为Gin(x,y)，出射光束的光场复振幅分布为Gout(x0,y0)，公式如下所示：

Gout(x0,y0)=H(x,y,x0,y0)·
t(x,y)·Gin(x,y)，

(5)

式中：H(x,y,ξ,η)为空间传递函数，在夫琅禾费衍射近似条件下，光束在远场的复振幅分布公式如式(6)所示：

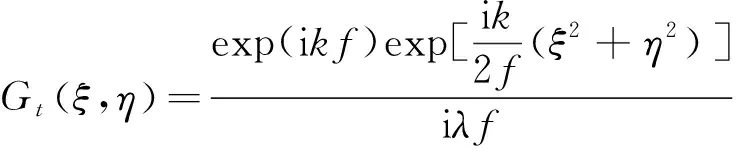
(6)

即

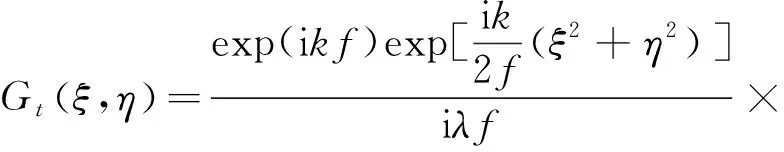
(7)

显然夫琅禾费衍射就是入射光场的傅里叶变换。Gt(xi,yi)为光束的远场分布，F{Gout(xo,yo)}为Gout(xo,yo)的傅里叶变换，f为空间光调制器距离远场的距离。由式(7)可知，光束在远场的分布取决于光调制器上各个点的相位值，改变各个点的相位，远场的衍射图将会被改变，因此可以通过改变相位值来逼近目标光束，称此过程为对目标光束的相位恢复过程。

3 多光束形成方法

3.1 子孔径法原理

当前使用液晶相控阵实现多光束的偏转常用的方法有部分孔径法、子孔径交叉法、迭代傅里叶变换法[14]，部分孔径法的原理是将液晶相控阵根据所需光束的多少进行划分，每个孔径所需的权重不同，得到的光束的偏转效率也就有一定的偏差。

本文中将使用LCSLM通过子孔径法来得到光束的二维偏转。在微波天线领域和相控阵雷达领域，子孔径的概念已得到了广泛应用，因此使用同样的原理，可以在液晶空间光调制器中引入子孔径来形成光学多波束，其原理是将液晶空间光调制器分为N份，在每部分内实现对单个光束的单独管理及控制。理论上说，N个子孔径可以形成N个独立的转向光束，每个子孔径的大小不一定需要相等，可以根据特定的需求进行随意分配，这里的LCSLM加载的是纯相位函数。显而易见，这种方法没有迭代过程，当多光束的数目较大时只有1/N个像素来进行干涉实现某一个光束的再现，而其他部分的相位值对该光束没有贡献，因此这种方法的光能利用率低。

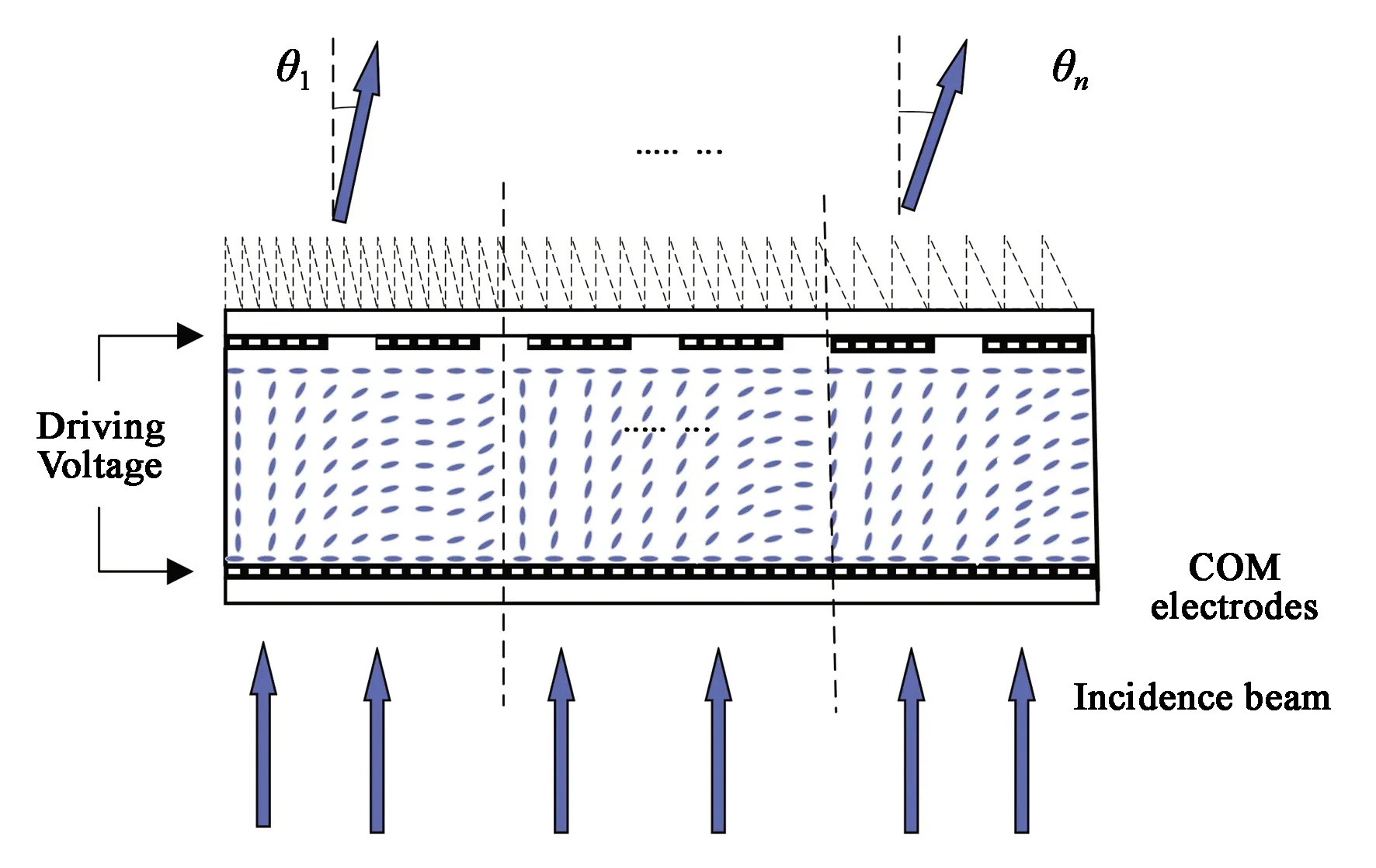
图4 子孔径法的示意图Fig.4 Schematic of the subaperture method

子孔径分布的原理图如图4所示，如图将空间光调制器分为n个部分，每个子孔径都有各自的相位差，可以分别表示为Δφ1，Δφ2，Δφ3···Δφn，每个子孔径也拥有不同的权重向量，权重向量不同，子孔径的大小也就互不相同。

设第n个子孔径的权重系数为an，an为大于0小于1的整数，L为液晶空间相控阵的大小，Ln为单个子孔径的长度。

各个子孔径区域中每个电极的相移量可以表示为φ1i,φ2i,φ3i···φni，根据上文可以得到相移量：

(8)

当高斯光束入射到LCSLM器件后，远场处的光束相干重叠区域可以表示成为：

Efar=E1far+E2far+···+Enfar，

(9)

式中:E1far、E2far···Enfar分别是由n个子孔径区域的相位调制所得。当要产生n个波束时，可以将LCSLM划分成n个区域，一维方向的相位分布如图4所示。

3.2 G-S相位迭代算法原理

国内外众多研究者开发了许多方法来解决相位恢复问题，其中Gerchberg-Saxton(G-S)相位迭代算法是最受欢迎的算法。G-S算法是由Gerchberg和Saxton在1972年提出的[15]，这种算法的基本概念是通过重复应用傅里叶变换和傅里叶逆变换对来找到空间域和频域中幅度约束相匹配的最优解。该算法已应用于不同的图像处理中[16-17]，通过实验和理论计算充分证明了算法的收敛性和有效性。因此本文主要是运用G-S算法与光寻址液晶空间光调制器相结合，设计出一种迭代傅里叶变换多波束形成算法。

光从入射面传播到出射面这一个过程是一个傅里叶变换过程，假设入射面的出射光振幅为E0，出射面的复振幅为E1，公式如下：

E0(x,y)=A0(x,y)exp[jφ0(x,y)]，

(10)

E1(u,v)=A1(u,v)exp[jφ1(u,v)]，

(11)

入射面与出射面的光场复振幅分布为一对傅里叶变换对，表示如下：

(12)

G-S迭代算法的计算步骤如下，首先，确定初始相位，通过给目标光场振幅叠加一个随机相位，将所得的复振幅分布进行逆傅里叶变换，提取相位值作为第一次迭代的相位值，这样可以缩短算法的迭代过程。将初始相位与入射光束的振幅A0(x,y)相结合形成入射光场，其次给定远场目标光束的振幅分布A1(u,v)，A0(x,y)和A1(u,v)即为算法在空间域和频域的幅度约束值。迭代开始将初始相位带入GS算法中进行傅里叶变换，对所得的频域空间的图像进行判断，看是否与期望的光强幅度A1(u,v)逼近，如果满足预设条件则退出程序，否则用A1(u,v)代替傅里叶变化的幅值，相位保持不变进行反傅里叶变换得到新的物空间像，保持相位不变用A0(x,y)代替幅值进行傅里叶变换，如此循环迭代直到得到合适的相位解。迭代过程的流程图如图5所示。

图5 G-S迭代傅里叶变换流程图Fig.5 Flowchart of G-S iterative Fourier transform

使用评价参数[18]η和RMS作为偏转效果的评价函数，衍射效率η定义如公式(13)所示，用来评价光束经过衍射元件后的能量损耗情况，其中Ii为目标光束的光斑强度，I0为观察平面出射波束的强度总和。

(13)

均方根误差RMS定义如式(14)所示，用来评价远场光斑与目标光斑的符合程度。

(14)

式中：g(u,v) 为观察平面波束的幅度值，A1(u,v)为期望的目标光束的幅度值。

4 仿真结果分析

4.1 子孔径法仿真分析

光寻址液晶空间光调制器的写入光为紫外光，读出光为红外光，我们设入射光束为波长为1 054 nm的高斯光束，有效光斑半径为3 mm，液晶相控阵的尺寸为5 mm×5 mm，利用第3节的理论仿真子孔径法的多波束的形成。

设目标光束的偏转角度为θ=(0，0.6°)和θ=(-0.6°，0)子孔径的权重分别为0.5和0.5，将子孔径进行均匀划分。仿真结果如图6所示。

由于部分孔径法的孔径大小为D/N，在上述仿真中孔径大小为D/2，因此导致了部分孔径法的分辨率较低。当N增大时，部分孔径法所得的光束的分辨率将持续降低，影响光束的衍射效率。

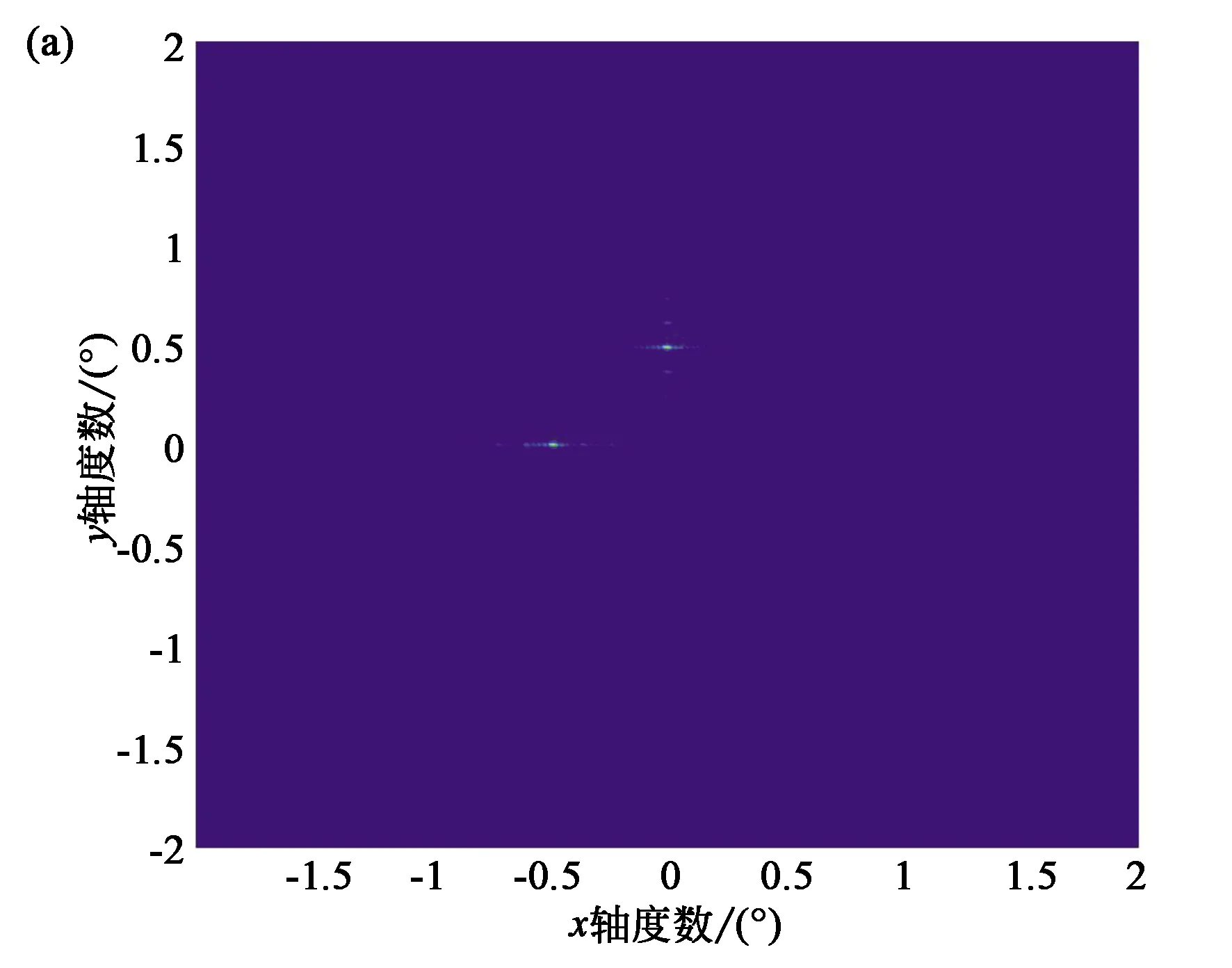
图6 (a)子孔径法的远场衍射图；(b)输入面的相位灰度图。Fig.6 (a) Far field distribution of the beam on subaperture method； (b) Phase diagram of input surface.

如图6所示，6(a)为观察平面的双波束的衍射图形，6(b)为输入面的相位灰度图，由图可以看出两波束的相位在入射面上平均分布，所占的权重值都为0.5。

4.2 G-S迭代傅里叶算法仿真分析

设目标光束为双光束，波束1和波束2在二维平面的偏转角度(θx,θy)分别为(-0.48°，0.60°)和(0.48°，-0.60°)时，不同采样数下光束的衍射效率不同，如表1所示。表1列出了采样数不同时光束的衍射效率的变化，可以看出采样数越大，光束的衍射效率越高。采样数为256时，光束的衍射效率为81.86%；采样数为512时，光束衍射效率达到91.94%；采样数为1 024时，光束的衍射效率为92.10%。采样数为1 024时，光束的旁瓣比采样数512时有轻微的减小，但是采样数取1 024时算法的耗时较长，所以这里不予采用。

在G-S算法中，不同的迭代次数下，光束的衍射效率也有所不同。设波束1和波束2在二维平面的偏转角度取(0.66°，-0.78°)和(-0.66°，0.78°)，仿真的最大迭代次数设置为100次，迭代过程中的远场幅度在x-z面的截面图如图7所示。

表1 不同像素数下的衍射效率Tab.1 Diffractive efficiency at different pixel numbers

图7为G-S相位迭代算法所求的的双波束远场分布图。图7(a)～(d)分别表示在迭代过程中不同时刻所产生的波束的远场分布。在迭代初期，光束的旁瓣较高且杂散光较多，光束的衍射效率为0.831 1。随着迭代次数的增大，光束的衍射效率逐渐升高。当迭代次数为100时，光束的衍射效率达到0.874 9。因此在仿真中我们取算法的迭代次数为100，采样数为512，对光束不同偏转角度下远场光强分布进行仿真分析，结果如图8所示。

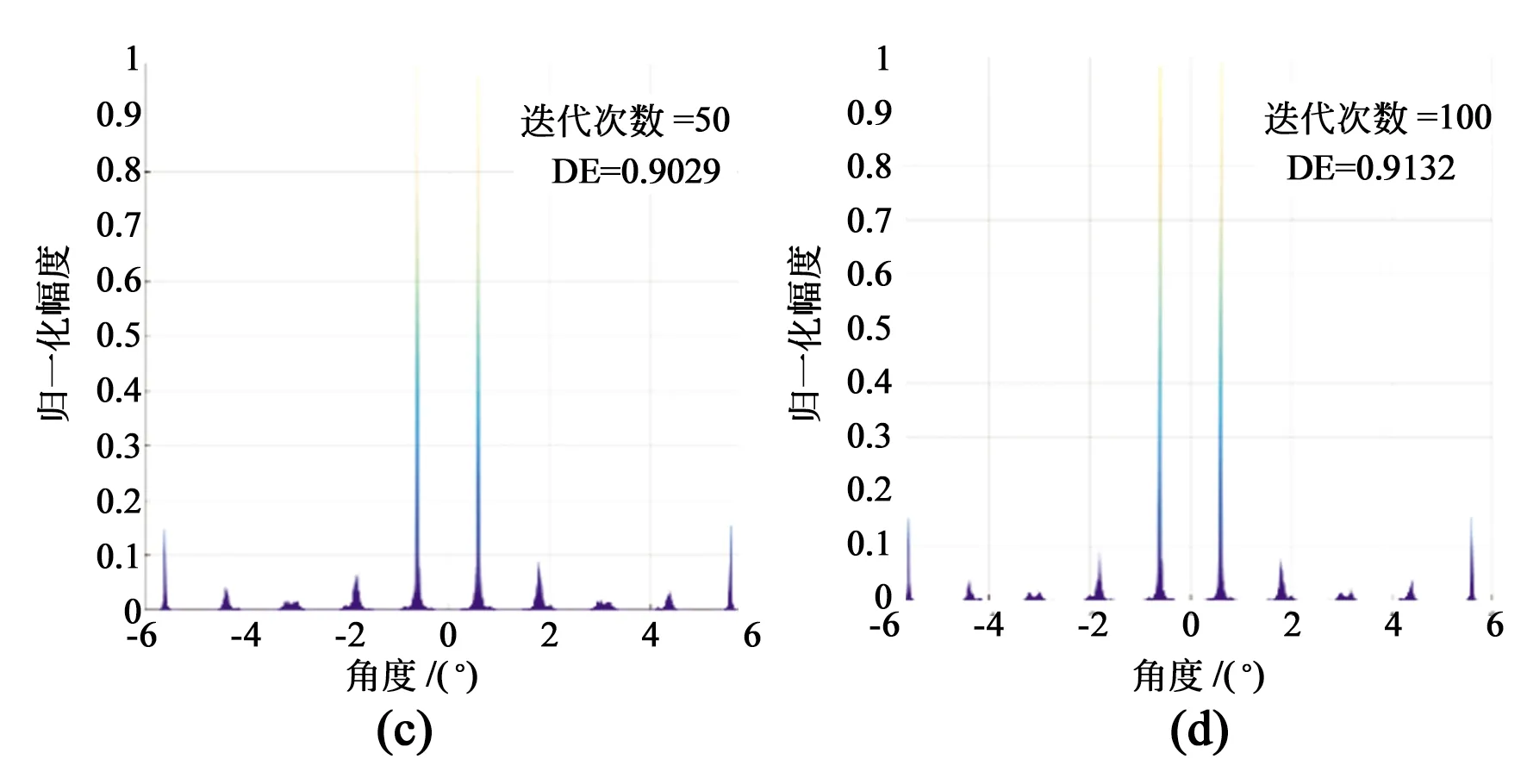
图7 G-S相位迭代仿真结果。(a)迭代次数为5；(b)迭代次数为10；(c)迭代次数为50；(d)迭代次数为100。Fig.7 Simulation results of the G-S iterative Fourier transform beam-forming method. (a) Formed amplitude pattern with iterations of 5; (b) Formed amplitude pattern with iterations of 10; (c) Formed amplitude pattern with iterations of 50; (d) Formed amplitude pattern with iterations of 100.

在图8(a)中远场光束的偏转角度(θx,θy)取(0.48°，0.60°)和(-0.48°，-0.6°)，通过仿真可以得到光束的衍射效率为0.909 9，光束的均方根误差为0.323 1。远场光束的衍射光强几乎分布在主瓣位置，次极大旁瓣归一化后分别分布在偏转角度为(-1.37°，2.38°)、(-0.603°，5.69°)、(0.47°、-5.60°)和(-5.69°，0.59°)等位置附近，其归一化强度在0.1～0.15范围内，主瓣和旁瓣比为20：3。(b)图中远场光束的偏转角度(θx,θy)取(1.2°，1.40°)和(-1.2°，-1.40°)，可以得到光束的衍射效率为0.667，光束的均方根误差为0.53。远场光束的衍射光强一部分分布在主瓣位置，其余能量分布在4束旁瓣位置，次极大旁瓣的位置分别为(-4.99°，1.92°)、(1.20°、-4.26°)、(-1.208°，4.267°)和(1.20°，4.26°)，最大旁瓣的归一化强度为0.48，主瓣和旁瓣强度比近似为2∶1。图9为G-S算法生成双光束的相位图，各个像素点的相位值在[0,2π]之间变化。由上述分析可以得到远场光束在不同的偏转角度下衍射效率不同，偏转角度越大，远场光束的衍射效率越小，均方根误差越大。

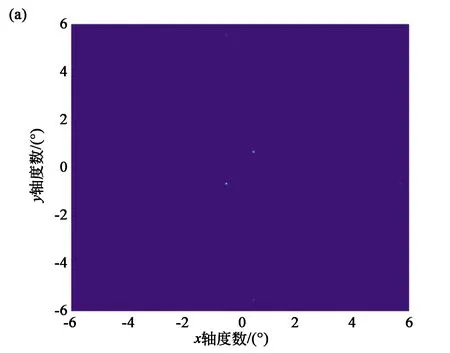
图8 不同偏转角度下，光束的远场分布图。(a)光束的偏转角度(θx,θy)取(0.48°，0.60°)和(-0.48°，-0.60°)；(b)光束的偏转角度(θx,θy)取(1.2°，1.40°)和(-1.2°，-1.40°)。Fig.8 Far field distribution of the beam at different deflection angles. (a) The deflection angle of the beam is (0.48°，0.60°)and (-0.48°，-0.60°); (b) The deflection angle of the beam is (1.2°，1.40°) and (-1.2°,-1.40°).

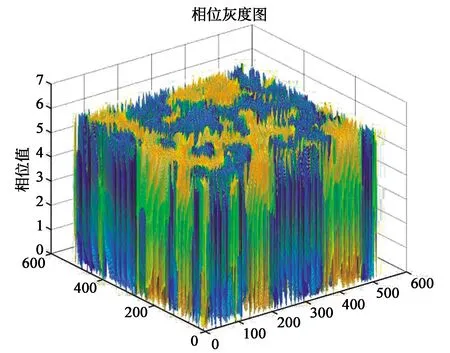
图9 G-S算法生成的双光束的相位图Fig.9 Phase diagram of the two beams generated by the G-S algorithm

5 改进的G-S相位迭代算法

G-S相位迭代算法相对于模拟退火算法和遗传算法存在收敛性好、运算速度快等优点。但是G-S算法是一种局部搜索迭代优化算法，对初始相位不够敏感很容易陷入局部最优值。因此，我们将G-S算法与模拟退火算法结合，提出了一种G-S算法的优化算法，同时我们将部分孔径法所得的相位作为G-S算法的初始相位进行迭代计算。

在算法开始，将部分孔径法所得的相位作为算法的初始相位，通过使用G-S算法计算得到相位屏的局部最优值；其次将上述的相位加入随机扰动，具体方法如公式(15)所示，ε(x,y)为[0,2π]之间的一个随机相位分布，b为一个扰动因子，其范围在[0，1]之间，这样的方法，相当于模拟退火算法中的升温过程。随后将加入扰动的相位屏加载进输入光场中，计算远场光束的分布。迭代完成后将加入扰动前和扰动后光场的误差评价函数RMS和RMS′ 通过预先设定的常数p来进行判断，当满足公式(16)时，储存扰动后的相位屏，否则保存原来的相位屏。在算法的计算过程中不断减小b和常数p的值，这样的过程相当于给系统不断降温。最后当迭代达到一定次数后，停止运算。

φ′(x,y)=φ(x,y)+b*ε(x,y)，

(15)

(16)

图10 不同偏转角度下双光束的衍射效率Fig.10 Diffraction efficiency of double beams at different deflection angles

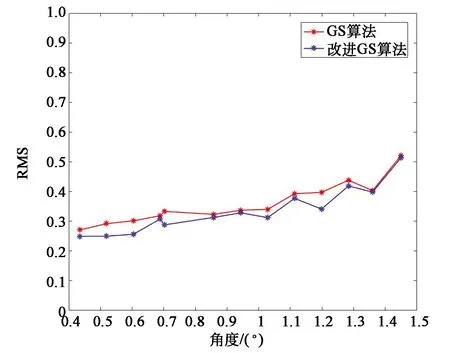
图11 不同偏转角度下双光束的均方根误差Fig.11 Root mean square error of double beams at different deflection angles

仿真结果如图10所示。从图10可以看出，随着光束的偏转角度增大，远场的光束的衍射效率逐渐降低，改进后的G-S迭代算法所得的衍射效率与原迭代算法相比，光束的衍射效率有明显提高，在偏转角度为1.2°时上升的幅度最大，上升幅度为0.03。图11展示了随着偏转角度增大双光束的均方根误差的变化规律，可以看出改进G-S迭代算法计算的光束的均方根误差值相比朴素G-S迭代算法有了一定的下降，在每个偏转角度处平均下降值为0.02。由此看以看出，将G-S算法进行改进后，算法的性能有了一定的提高，远场光束与目标光束更加接近。

6 结 论

本文使用改进的G-S优化迭代算法，以在像面干涉而生成多光束束斑为目标函数，确定了输入面上DOE的二维相位分布。该方案的特点在于通过确定OASLM上DOE面适当的二维相位分布，以高斯平行光束通过DOE以后重构波阵面，生成多个强度受控、角度受控的束斑，以此实现平行入射的光束在二维任意角度的分束和偏转。模拟结果表明，改进的G-S算法计算得到的远场光束在0°～1.4°偏转角度内，衍射效率和均方根误差分别在0.8～0.95和 0.2～0.5范围内波动，相比朴素G-S算法所得到的结果有了明显提高。