基于MSP430的高精度光照功率计设计
2020-06-16王磊,朱可,王军,,何昕
王 磊,朱 可,王 军,,何 昕
(1. 苏州科技大学,江苏 苏州 215009;2. 中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033)
1 引 言
传统固化行业采用高压汞灯快速固化,但污染严重,逐渐被LED灯所取代。传统检测LED光功率采用的是积分法,采用固定时间段内检测光能量除以固定时间得到平均光功率。此方法采集的光能量存在采集误差,求得平均值后的光功率也只能表示固定时间段内光功率的平均值,与实时值存在误差;在软件除法处理中存在误差,进一步扩大了误差。
为提高光功率计的精确度,本文采用光电传感器转换的紫光信号,经过负反馈电流放大、差分放大和滤波电路,并通过24位高精度AD芯片转化为数字信号,结合递推平均滤波法和中位值平均滤波算法得到精确的光功率值,并在LCD上显示实时数值和测量曲线。实验证明,所设计的光照功率计误差低于0.3%,具有功耗低、系统稳定、显示界面友好的优点,可以存储测量数据,显示光功率曲线。
2 总体设计
高精度光照功率计包括前端光照采集、按键控制、数据存储和显示4部分。光电传感器将光转换成微弱电流信号,经过负反馈电流放大电路、差分放大和滤波电路转换成电压信号[1-2],经过AD模数转换芯片转换为数字信号,主控制器通过数字滤波将数据存储,并将功率值实时显示在屏幕。按键可以切换显示界面内容。总体框图如图1所示。
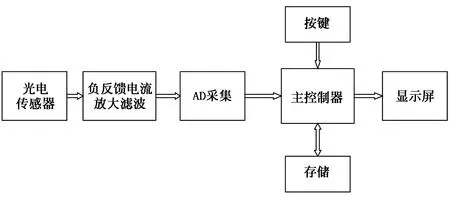
图1 系统总体框图Fig.1 Block diagram of system
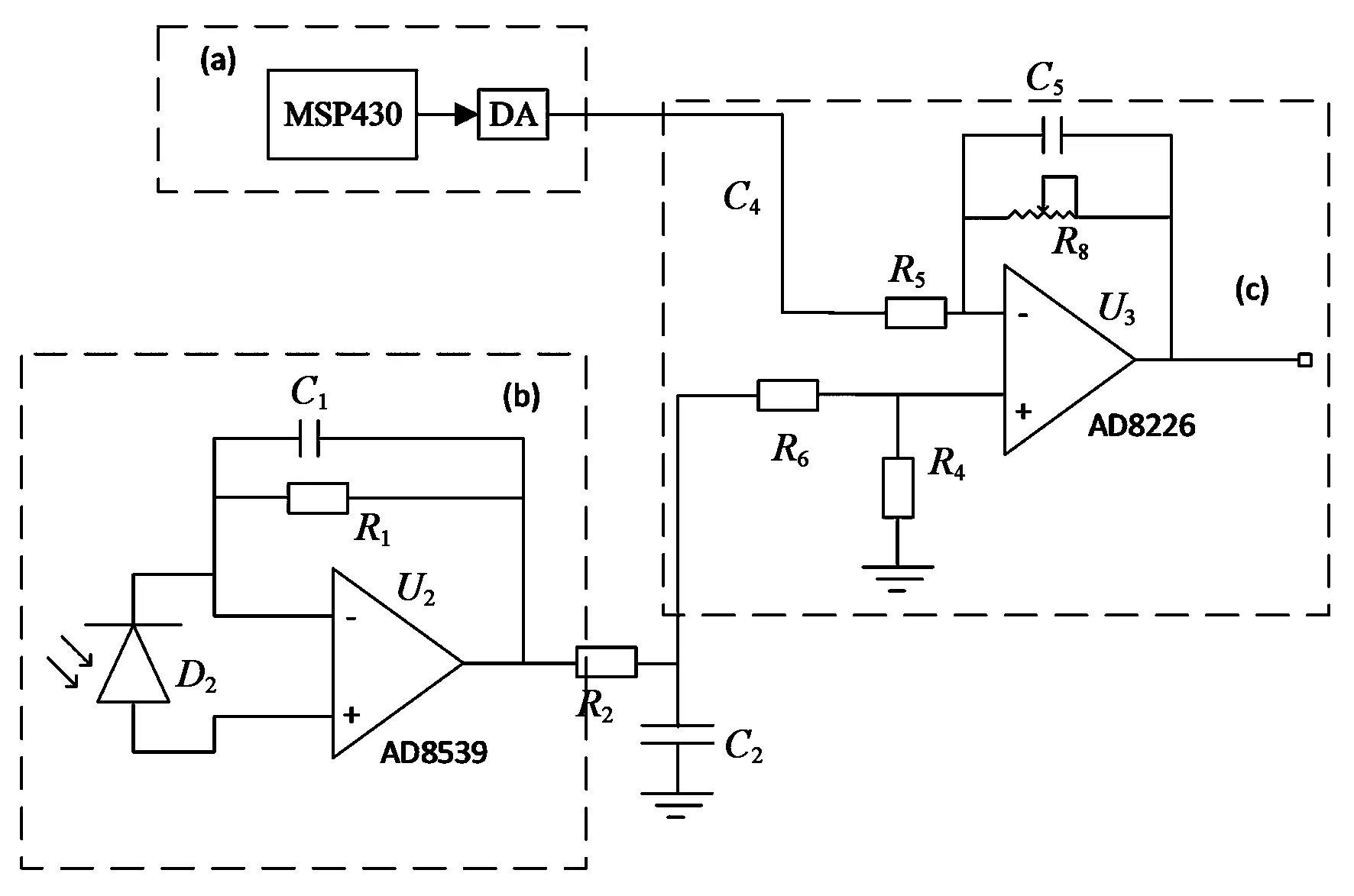
图2 光照前端采集电路图Fig.2 Circuit diagram of optical collection
3 功率计硬件设计
3.1 校零光检测前段采集电路设计
在图2(b)所示电路中,硅光传感器D2将光转换为电流信号,经过R1精密电阻和U2放大器构成的负反馈电流放大电路后输出(Vout)b,且
(Vout)b=-(ID2×R1),
(1)
系统电压噪声频谱密度为(1 μA电流转1 V信号):
(2)
其中电阻热噪声:
(3)
其中:k为波尔兹曼常数,T为绝对温度[3],由式(2)得系统电压噪声频谱密度为:
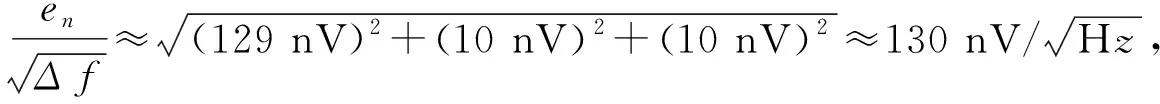
由于采集探头存在环境光的暗电流,所以为提高采集精度,需要将暗电流消除。图2中(a)部分在(c)部分的差分放大电路的负端接入一个可编程的DA芯片输出可调电压以消除探头中的暗电流,实现校零功能。经过运算放大后(Vout)c:
(4)
其中:V环境为软件校零DA输出的电压,滤除环境光中的暗电流噪声。
3.2 24位高精度采集电路设计
24位高精度AD采集芯片具有单端采集、差分采集等多种模式,传统的单端采集一端接入处理后的电压信号,一端接地,但是此方法接地回路干扰较大、抗环境共模干扰能力较低,所以采用差分采集模式。可编程AD芯片设置采集增益为1,更新速率为4.17 Hz时,均方根噪声为40 nV。将图2(c)部分输出的(Vout)c单端电路转为图3差分电路,图中R2=R3、R1=R4、R6=R7、R5=R8,从而差分电压两端输出电压为:
(V)+=(Vout)c+1.25,
(5)
(V)-=-(Vout)c+1.25,
(6)
MSP430主控制器通过SPI接口配置AD7793[4],并且读取差分转换的数据。
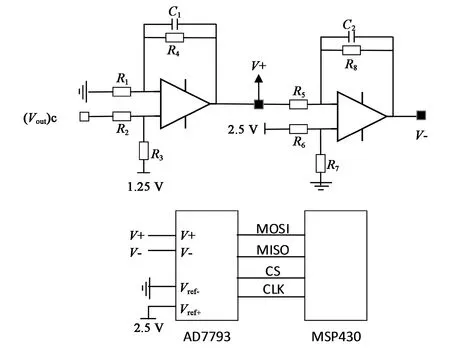
图3 单端转差分采集电路图Fig.3 Circuit diagram of differential acquisition
4 功率计软件设计
4.1 AD采集及校零算法设计
在环境光下,由于暗电流,硅光传感器输出存在环境噪声,通过AD采集,此时会在显示屏上显示一个环境光功率,通过校零,MSP430主控制会通过DA产生一个对应的电压,通过减法电路,滤除环境光带来的暗电流,循环执行直到在检测环境下显示屏上显示实时功率为0完成校零[5-7],流程图如图4所示。
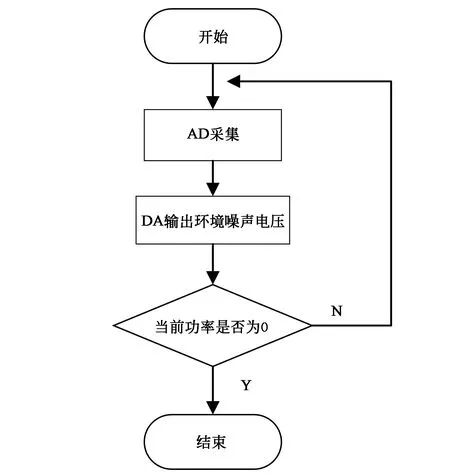
图4 校零流程图Fig.4 Flowchart of check to 0
4.2 数字滤波算法设计
本文融合递推和中位值平均滤波算法的优点,有效抑制周期性干扰,且平滑度较好。将连续采集的N个光功率P看成一个队列,队列长度固定为N。每次采样到一个新的紫光功率Pn数据放入队尾,去掉队首的Pn-10。然后将{Pn-9,Pn-8,…,Pn}N个功率P进行冒泡排序,去掉Pmax和Pmin,再将队列中的N-2个数据进行算术平均运算:
(7)
就可获得当前功率值,流程图如图5所示。

图5 数字滤波流程图Fig.5 Flowchart of digital filter
4.3 LCD曲线平滑算法设计
直接将光功率值显示,曲线尖锐,而实际应用中光功率的测量变化趋势更为重要,采用Savitzky-Golay滤波器[8]将测量值滤波后曲线显示平滑。采集到的光功率值P(N)中连续的一组数据为P(n),其中n=-M,-(M-1),…,0,…,M-1,M。将这组数据滤波后得到y(n),确定式(8)中a0,a1,…aT系数可确定y(n)多项式:
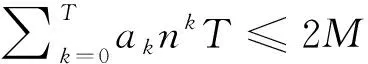
(8)
直接计算多项式的所有系数比较复杂,由于式(8)中y(0)=a0,为降低MSP430运算复杂度,减小功耗,只需求a0系数求出P(i)数据中心值P(0)的拟合值y(0)。然后将选取的P(i)当作一个“窗口”往右平移求中心值,最终得到P(N)滤波后的数据y(N)。y(N)与P(N)存在拟合误差,设总的误差平方和为
(9)
为使拟合曲线误差最小,令E对各系数的导数为0,即
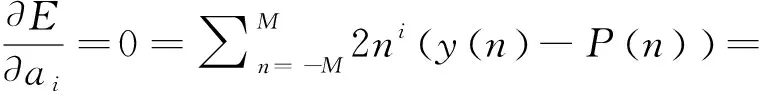
(10)
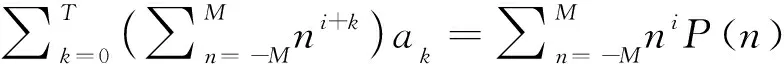
(11)
在实际过程中,根据多次尝试发现,当T=3,M=3时效果最佳,从而得:
(12)
将拟合出的值通过画点函数在LCD屏幕上显示[0]。
5 实验结果与分析
本文前端采集电路与传统法对比,通过示波器可以看出,图6光电传感器信号放大滤波后,信号稳定,纹波小于20 mV,有效滤除了环境噪声;而图7传统法信号纹波高达100 mV,包含有50 mV环境噪声。
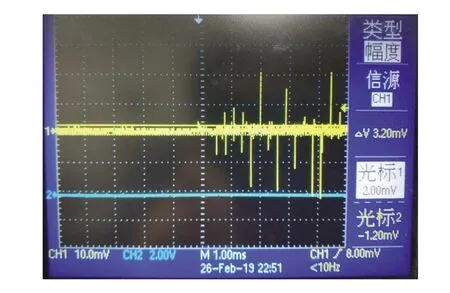
图6 本设计放大滤波后信号Fig.6 Waveform of our amplification filter
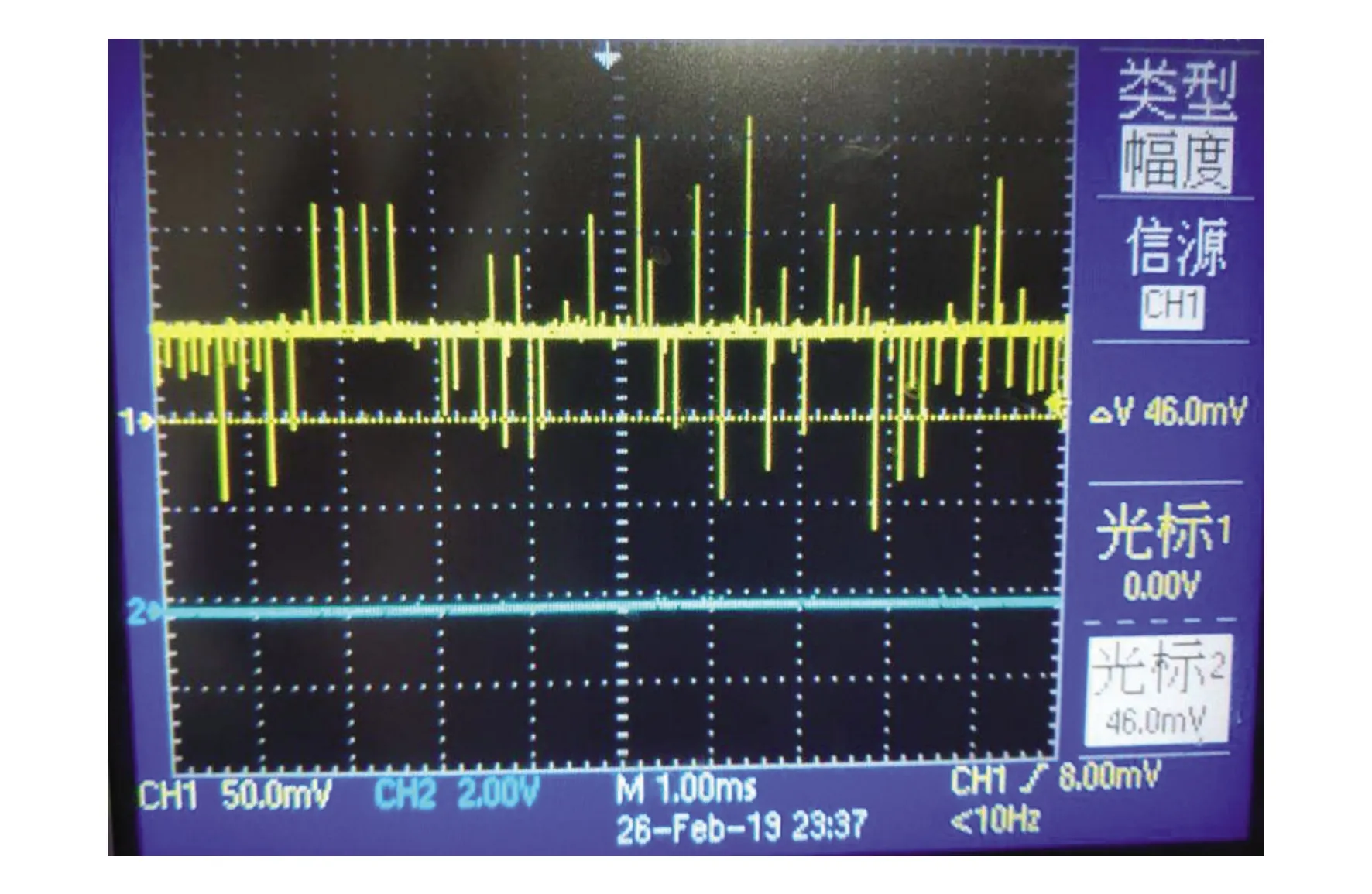
图7 传统放大滤波后信号Fig.7 Waveform of traditional amplification filter
在相同测试环境下,用传统法牛尾的检测仪器和本测试法的仪器对同一个面光源在不同强度下进行检测,所得数据如表1所示。从测试数据中可知,牛尾的测试值总是比光谱仪测的实际值大,这是由于其中的环境噪声未滤除所导致,而本文所测的数据与标称值误差小于0.3%,两种测试数据与标称值对比误差如图8所示。
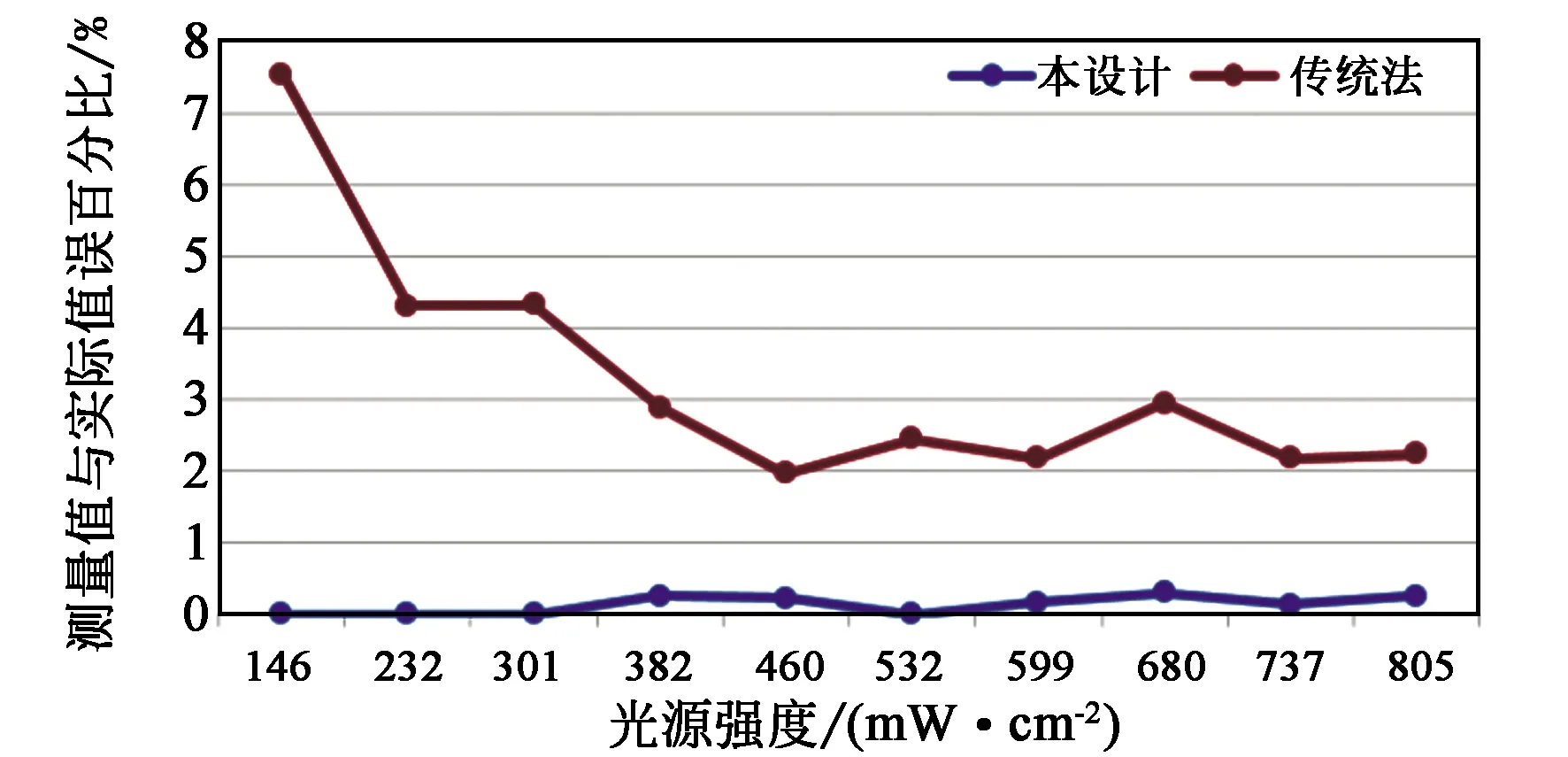
图8 面光源不同强度下检测数据及误差分布图Fig.8 Graph of two detecting methods under different luminance error
表1 同一光源不同强度两种检测方法测得数据
Tab.1 Results of two detecting methods under different luminance with LED (mW·cm-2)
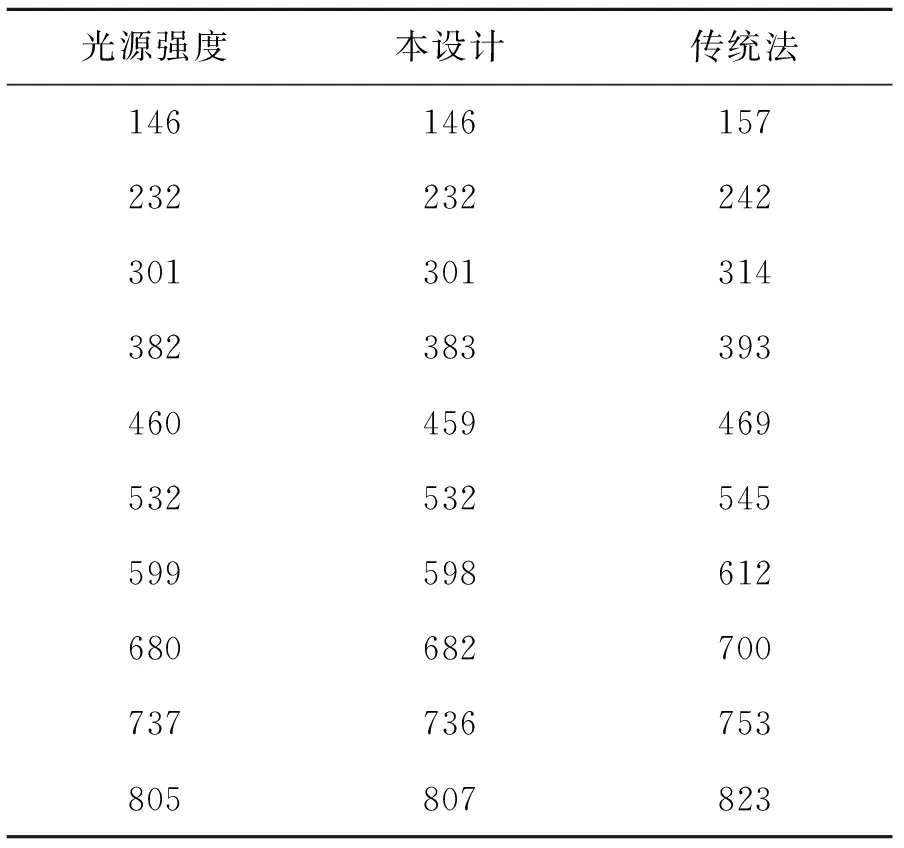
光源强度本设计传统法146146157232232242301301314382383393460459469532532545599598612680682700737736753805807823
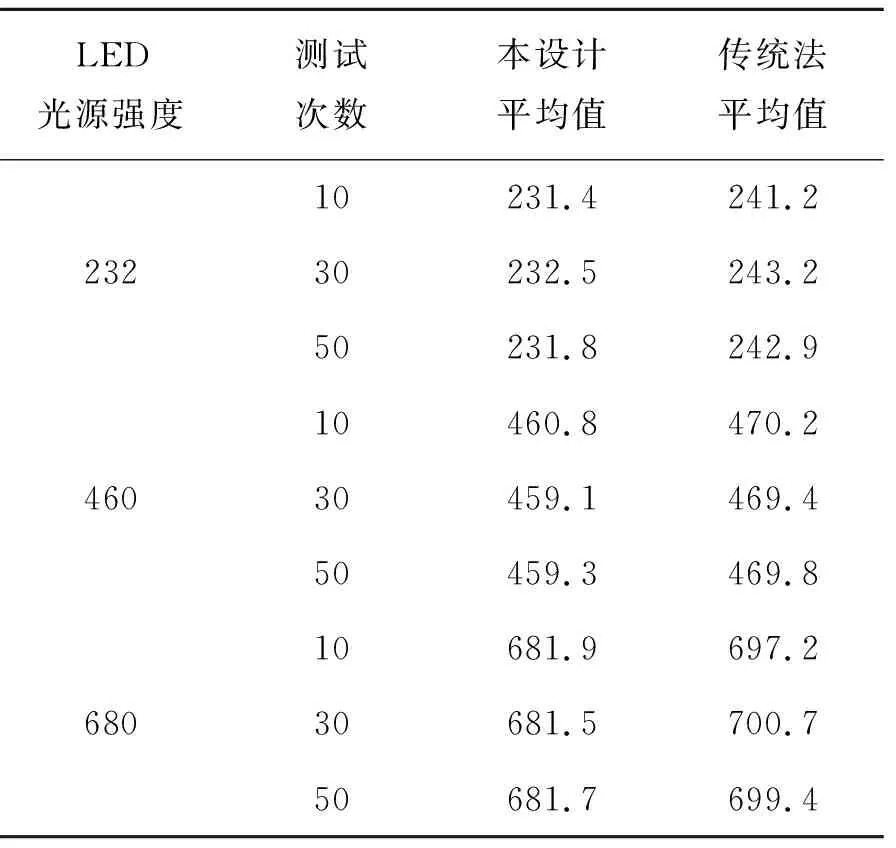
为消除测试的偶然误差,同一测试环境下,同一面光源,针对232,460,680 mW/cm2三个代表性强度,两个检测仪器分别检测10,30,50次,所得测试数据平均值如表2所示,误差曲线如图9所示。测试数据可知校零光检测前段采集电路能够消除环境噪声,并且精度高,误差小。
表2 同一光强不同强度两种检测方法多次测的数据平均值
Tab.2 Average value of two detecting methods under different luminance with LED (mW·cm-2)
LED光源强度测试次数本设计平均值传统法平均值10231.4241.223230232.5243.250231.8242.910460.8470.246030459.1469.450459.3469.810681.9697.268030681.5700.750681.7699.4
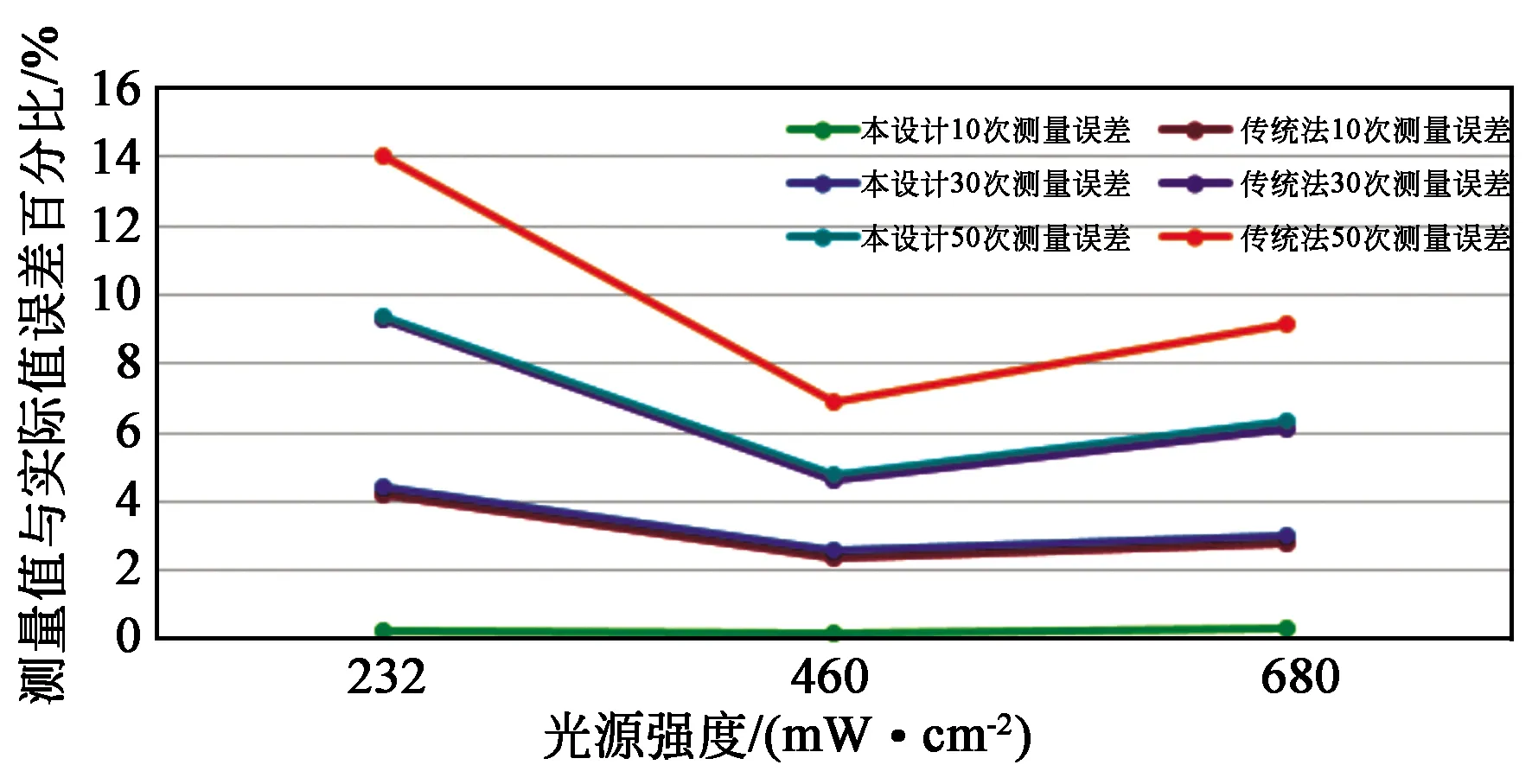
图9 面光源不同强度下多次检测数据误差分布图Fig.9 Graph of two detecting methods under different luminance and repeatedly detecting error

图10 未滤波曲线Fig.10 Waveform without filter
图11 滤波后曲线Fig.11 Waveform with filter
针对存储一次检测的数据在LCD上模拟出曲线,图10是直接将数据显示在LCD上,图11是将数据经过Savitzky-Golay数字滤波器后显示的LCD。对比可看出曲线明显平滑,并且曲线特性也显示在LCD上。
6 结 论
经过多次测量数据对比,本设计采用的环境噪声滤除、负反馈电流放大前置采集电路能有效滤除环境噪声;采用的24位高精度数模转换和多数字滤波器相融合的方法能显著提高光源光功率的采集精度和稳定度,可以广泛应用在工业LED光功率测量领域。
