基于1：2s规则的重复抽样质控策略性能评价

张 裕， 彭爱红， 杨丽华， 余启华

（湖南省第二人民医院 湖南省临床检验中心，湖南 长沙 410007）

目前，临床实验室在室内质量控制中，普遍的做法是当结果超过1：2s界限后进行复查，由于1：2s存在较高的假失控概率，Westgard最初也只将其作为警告规则而不是失控规则[1]。但临床实验室从第1次检测到重复检测超过1：2s界限的质控物后，这一系列的质控活动所获得的误差检出概率及假失控概率是否有变化，却往往被忽略。PARVIN等[2]提出了一种基于1：2s规则的重复抽样质控策略（repeat 1：2sQC rule），评估了常见的几种重复方案的效果，为临床实验室提供了一种备选的质控方案。

1 基于1：2s规则的重复抽样质控策略

1.1 规则介绍

当第1次检测的质控数据有超出±2s界限的情况时，可按4种方案进行重复检测，并评价质控数据是否可接受。（1）方案一。如果第1次检测的质控结果在±2s界限内，则接受。否则，重复检测超出质控界限的质控物，若重复检测的质控结果均在质控界限内，则接受。否则，拒绝本次结果并开始进行失控分析。（2）方案二。如果第1次检测的质控结果均在±2s界限内，则接受。如果有大于1个质控结果超出质控界限，则拒绝。否则，重复检测超出质控界限的质控物，若重复检测的质控结果在质控界限内，则接受。否则，拒绝本次结果并开始进行失控分析。（3）方案三。如果第1次检测的质控结果均在±2s界限内，则接受。否则，重复检测所有质控物，若重复检测的质控结果均在质控界限内，则接受。否则，拒绝本次结果并开始进行失控分析。（4）方案四。如果第1次检测的质控结果均在±2s界限内，则接受。若有多于1个质控结果超出质控界限，则拒绝。否则，重复检测所有质控物，若重复检测的质控结果均在质控界限内，则接受。否则，拒绝本次结果并开始进行失控分析。

根据Parvin等[2]的重复抽样策略，利用图示的方式来解释。采用3个水平质控物（N=3）的重复抽样质控策略示意图见图1，采用2个水平质控物（N=2）的重复抽样质控策略示意图见图2。

从图1、图2中可以看出，方案一、二如果出现超过±2s界限，在满足重复检测条件时，只复检超出了界限的质控物；而方案三、四如果出现超过±2s界限，在满足重复检测条件时，则会复检所有水平的质控物，包括初始结果在±2s界限内的质控物。图1、2提供了4种方案的简单示意，图中只画出同时超出+2s的情况，若有超出-2s的情况，亦使用重复策略进行操作。重复检测后的数据必须在±2s范围之内，否则判断为失控，临床实验室应按流程查找失控原因[3]。

图1 采用3个水平质控物（N=3）重复抽样质控策略示意图

图2 采用2个水平质控物（N=2）重复抽样质控策略示意图

1.2 计算公式介绍

误差检出概率（Ped）是评价质控规则功效最直接的指标，由于可能发生重复检测质控物的情况，因此重复抽样策略将轻度增加控制物的使用频率，质控检测结果的个数为2～4个（2个水平质控物）或3～6个（3个水平质控物），4种方案的Ped和每次质控评价过程的平均质控检测个数（NQ）的计算公式为：（1）方案一。Ped（SE）=1-[1-P1（SE）2]N，NQ=N[1+P1（0）]；（2）方案二。Ped（SE）=1-[1-P1（SE）]N[1+NP1（SE）]，NQ=N{1+[1-P1（0）]N-1P1（0）}；（3）方案三。Ped（SE）={1-[1-P1（SE）]N}2，NQ=N{2-[1-P1（0）]N}；（4）方案四。Ped（SE）=1-[1-P1（SE）]N{1+NP1（SE）[1-P1（SE）]N-1}，NQ=N{1+N[1-P1（0）]N-1P1（0）}。

1.3 利用Excel软件计算Ped及NQ

根据前述计算公式，可利用Excel软件进行函数编辑。计算Ped（SE）所涉及的参数包括在临界系统误差下的误差检出概率P1（SE）及质控物个数（N）。计算NQ所涉及的参数包括在临界系统误差为0时的误差检出概率P1（0）及质控物个数（N）。而P1（SE）、P1（0）的计算又涉及到2个参数，即质控界限s（1：2s规则取值为2）及临界系统误差（ΔSE），需使用NORMSDIST函数进行计算。4种方案的Ped及Excel函数见表1、表2；NQ及Excel函数见表3。

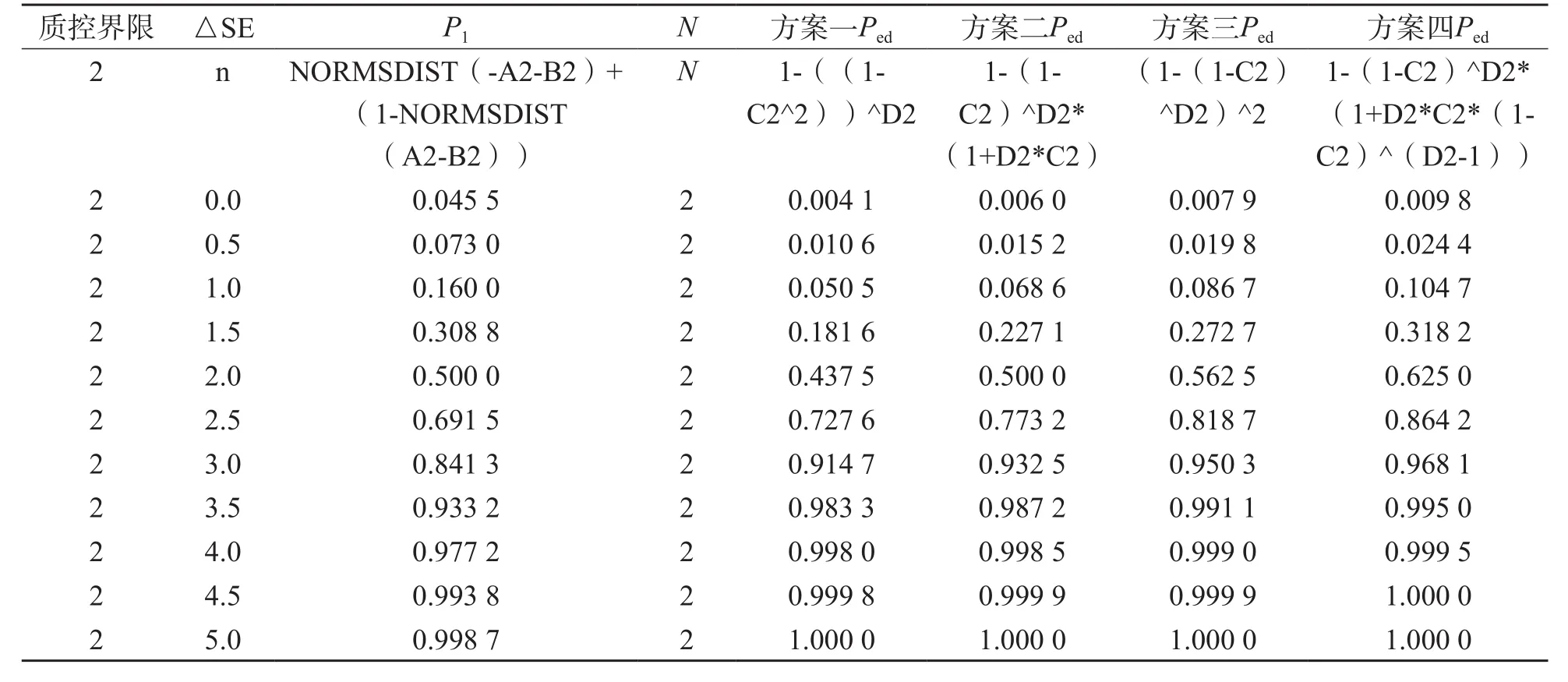
表1 4种方案Ped及Excel函数（N=2）

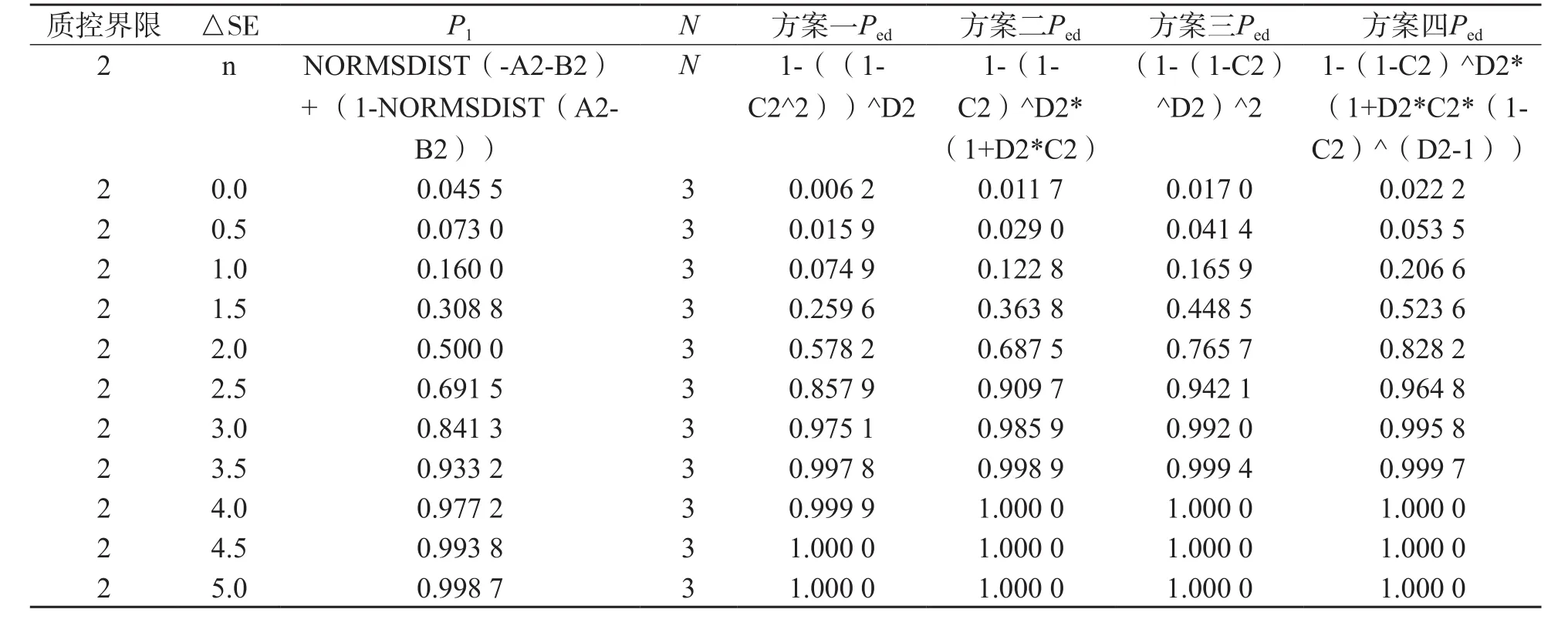
表2 4种方案Ped及Excel函数（N=3）

表3 4种方案NQ及Excel函数

1.4 与常用质控规则比较

通过计算4种重复抽样策略的功效，比较结合1：2s、1：3s和2种多规则1：3s/2：2s/R：4s、1：3s/2of3：2s/R：4s方案的功效函数，结果显示，重复抽样策略在临界系统误差较小时，其功效曲线更接近于1：3s规则，具有很低的假失控概率；而在临界系统误差较大时，其曲线更接近于1：2s规则，具有很高的误差检出概率。4种方案中，方案四具有相对最高的功效，方案一的功效相对最低。重复抽样策略结合了1：2s和1：3s的优点，其功效可与多规则媲美，甚至高于1：3s/2：2s/R：4s及1：3s/2of3：2s/R：4s的 功效。见图3。

图3 4种方案与其他常用规则功效函数图

1.5 利用Excel软件绘制标准化OPSpecs图。

重复抽样策略不但方便应用手工绘制功效函数图，也可手工绘制标准化的OPSpecs图。

利用临界系统误差的计算公式，结合Excel软件的“单变量求解”功能，可算出当Ped达到90%水平时，各种方案的临界系统误差值（表4）。根据计算公式：Bias=TEa-（△SE+1.65）×CV[4]，式中Bias为偏移（bias），TEa为允许总误差（allowable total error），CV为变异系数（coefficient of variation），可绘制出重复抽样策略的标准化OPSpecs图，见图4。

图4 具有90%分析质量保证的标准化OPSpecs图

表4 具有90% Ped时的△SE及允许不精密度

当N=2时，4种方案均处于4西格玛性能范围，若参照Westgard西格玛规则[5]，4西格玛性能水平时，采用的质控方案为1：3s/2：2s/R：4s/4：1s，N=4，R=1或N=2，R=2，使用起来相对复杂。若按照重复抽样质控策略，当检测项目西格玛值≥4.27时已可选用，当西格玛值≥4.59时，4种方案均可达到90%的分析质量保证。而当N=3时，重复抽样质控策略能监控到较低的3西格玛性能范围，西格玛值≥3.84时已可选用，能对检测质量较差的项目提供质量保障，当西格玛值≥4.27时，4种方案均可达到90%的分析质量保证。

2 总结

对于临床实验室而言，最耳熟能详的质控规则莫过于“Westgard多规则”，但实际进行质控时并非只有一种规则，新的质控方案不断涌现。值得注意的是，质控规则能否被临床实验室接受，最关键的因素是“易用性”。如果质控规则的计算过于复杂，如“Z2质控规则”，或必须依赖专用软件，则在临床实验室实际工作中不具备实践性。简单、易用、高效的质控策略才更受临床实验室青睐[6]。重复抽样质控策略只涉及到1个1：2s规则，判断失控情况非常方便；在规则的理解上很简单，提供了4种方案供实验室选择；可利用办公软件绘制功效函数图并计算实验室的实际功效；重复策略结合了1：2s和1：3s的优点，具有高误差检出概率和低假失控概率，能为西格玛性能水平较低的检测项目提供质量保障。临床实验室在设计室内质控程序时，可根据实验室的质量水平，考虑选择重复抽样质控策略作为质量保证的方案之一。