多重动力吸振器对高速列车地板振动的控制
2020-06-16尤泰文周劲松孙维光陈江雪
尤泰文,周劲松,孙维光,宫 岛,陈江雪
(1.同济大学 铁道与城市轨道交通研究院,上海 201804;2.中车青岛四方机车车辆股份有限公司技术中心,山东 青岛266000)
随着高速动车组运行速度提高及轻量化设计的广泛使用,车体弹性振动逐渐增大,导致地板等内装结构局部振动时有发生。地板作为动车组的关键部件,面积大,且弹性模量远低于车体型材模量,若其减振设计不当则极易发生局部共振,进而大大削弱乘客的乘坐舒适性。因此,有效控制地板振动对提高车辆运行品质及改善乘客舒适性具有重要意义。近年来,研究人员对高速动车组车体的振动研究,往往集中于车体结构振动,较少关注车身局部及内饰件振动。
例如,宫岛等采用匀质欧拉-伯努利梁建立了车辆垂向刚柔耦合动力学模型,研究了车体刚度对车辆振动的影响,指出运行速度的不断提高对车体垂弯频率提出更高的要求[1]。Suzuki等在欧拉-伯努利梁基础上,将车体看做三段变刚度Euler梁,建立车辆垂向动力学模型,用以研究车体振动问题,但是该模型只能研究车体整体垂向弯曲振动,而无法研究地板等局部结构对乘坐舒适性的影响[2]。周劲松等采用动态缩聚理论对车体有限元模型进行缩聚计算,建立包含弹性车体的三维刚柔耦合车辆系统动力学模型,研究了车体的整体弯曲振动对车辆运行舒适度的影响[3]。不难看出,这些研究由于受其理论模型的限制,均将车体及地板等内装结构考虑为整体或者未考虑地板振动等局部结构对乘坐舒适度的影响,因此,对于精确预测分析地板等局部结构振动对乘坐舒适性的影响存在很大误差。
目前,针对动车组地板振动控制问题主要是采用经验方法进行研究,如大面积优化地板支撑结构[4]、铺设高阻尼地板布[5]等。这些方法无法对地板局部振动进行精准控制。马梦林等针对高速列车出现的脚感发麻现象,采用振动传递测试确定振动产生原因,并通过优化地板支撑元件刚度进行减振[6]。郑路等通过试验分析指出,不同的地板支撑材料对地板振动具有显著影响,并给出了不同复合材料在有限元建模时的刚度等效方法[7]。
近来,国内某型动车组在线路运营时,屡屡出现车体局部振动导致脚感发麻现象,为对该地板异常振动进行治理,本文首先结合线路试验,分析地板局部振动产生原因;随后基于多自由度结构振动原理,建立包含多重动力吸振器的地板振动控制模型,同时根据车体结构参数建立包含地板的精细化有限元模型,对地板局部振动进行仿真模拟,随后研究多重动力吸振器在控制地板振动中的应用。分析吸振器最佳安装位置及最优参数对地板局部振动控制效果。
1 地板振动试验分析
本文对某存在地板局部振动的高速动车组进行线路试验,分析其成因。在进行线路试验时,基于UIC标准[8],于前转向架上方车体、车体中部及后转向架上方车体地板面布置加速度传感器。
当车辆运行速度为300 km·h-1时,前、后转向架上方及车体中部地板振动幅频曲线测试结果如图1所示。图1中,车体中部地板在10 Hz、30 Hz附近的振动明显大于前、后转向架上方,特别是车体中部地板在10.5 Hz、33.6 Hz附近出现了强烈的振动能量集中。为进一步明确地板局部振动原因,分析各点振动传递率,以线路试验时空气弹簧上方的振动响应作为输入,地板测点作为输出,获得300 km·h-1速度级时各个输出点与激励点之间的振动传递关系。由结果可知,空簧测点到地板中部的振动传递率幅值在30~40 Hz时明显大于其他频段,表明地板在30~40 Hz减振效率不佳。由于该频段恰好覆盖了人体腿部振动敏感频段,继而出现脚感发麻现象,影响旅客乘坐舒适性[9]。
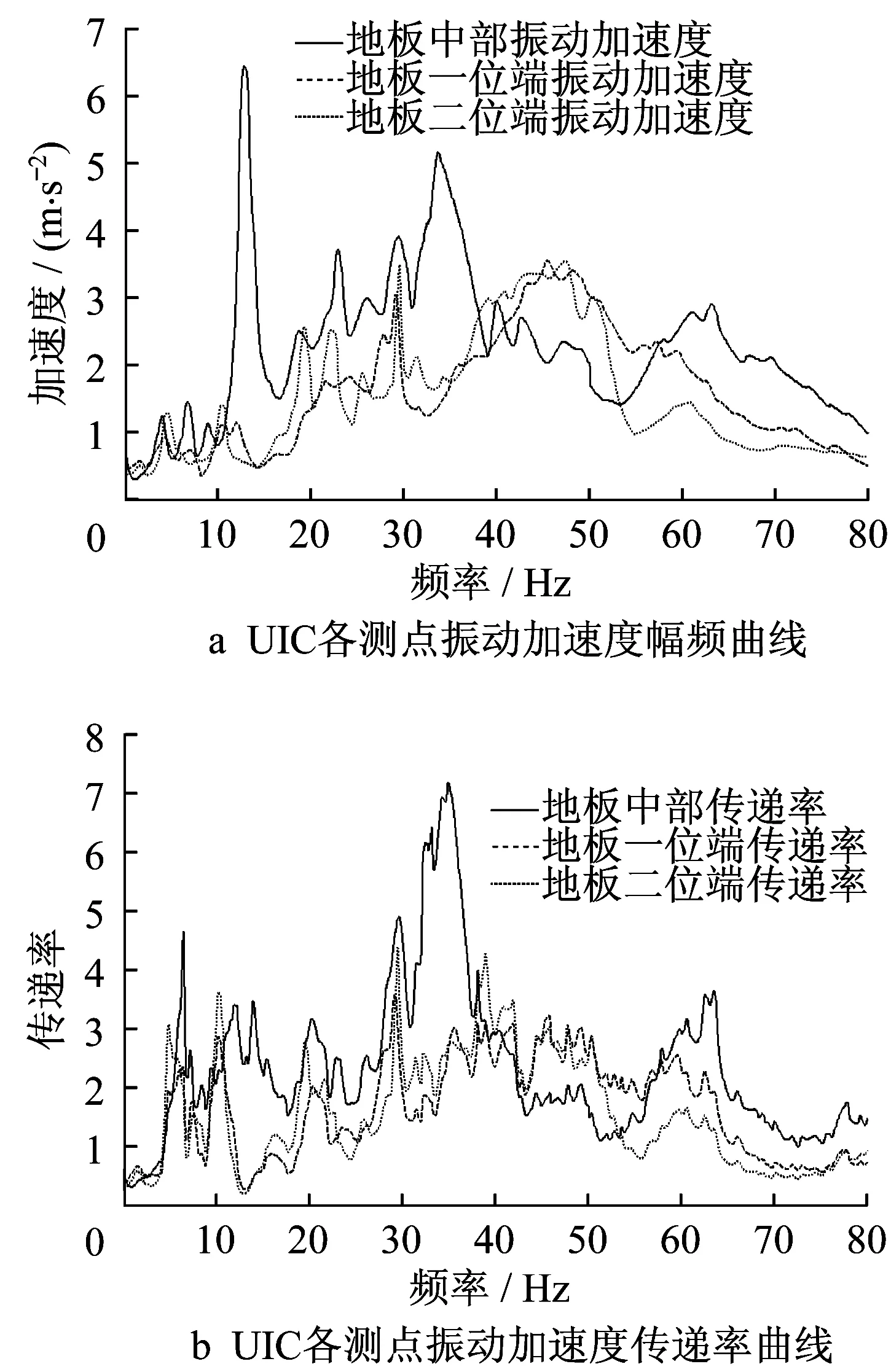
图1 转向架上方及车体中部地板振动幅频曲线测试结果Fig.1 Measured vertical vibration acceleration spectrum and transmissibility at ride quality testing points
2 地板振动模型建立
对于已投入运营的车辆而言,如果采用修改地板结构的方式来改善地板局部振动,则需要付出较高的成本和代价。而动力吸振器能够以较小的结构吸收局部振动,对既有结构改动较小,且成本低。因此,本文尝试采用动力吸振器以控制地板局部振动。将车体及地板视为如图2所示的振动系统,在地板某位置安装p个动力吸振器用于控制该处地板的局部振动,每个动力吸振器的质量、刚度、阻尼分别为mi、ki、ci,动力吸振器自身位移为zi,与车体的相对位移为vi,对第i个动力吸振器有如下振动方程:

车体的运动方程为
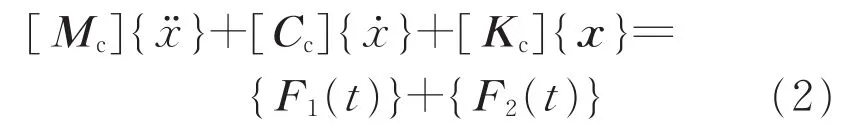
式中:[Mc]、[Cc]、[Kc]分别为车体的质量矩阵、阻尼矩阵和刚度矩阵;{x}为地板的位移列向量;{F1(t)}为车体结构受到的激励;{F2(t)}为动力吸振器对地板的作用,因此
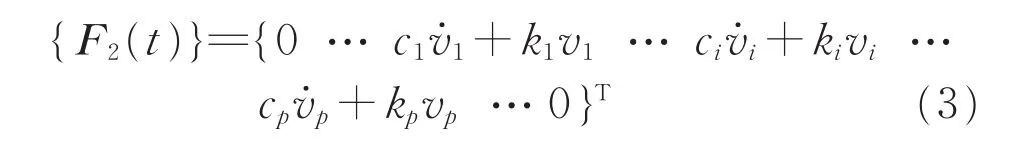
设车体结构振动控制振型列向量[Φ]=[φ1φ2…φn],其中n为结构的总自由度。另有振型的子向量[φji]⊂[Φ],[φji]=[φj1φj2···φjp]T,为第i个动力吸振器所在位置的振型幅值。
由模态叠加原理可知,地板结构在任意激励下的响应是其各阶模态响应的叠加,而被控制振型的贡献占优,因此近似认为

式中:[φj]为贡献占优模态;qj该阶模态对应的模态坐标;xji为对地板在贡献量最大的模态下第i个动力吸振器处的垂向位移,则相对位移vi为
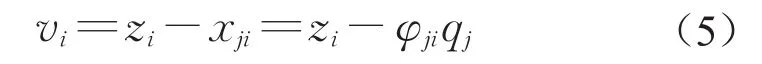
将式(4)代入式(2),两边同时左乘[φj]T,基于模态正交性,令
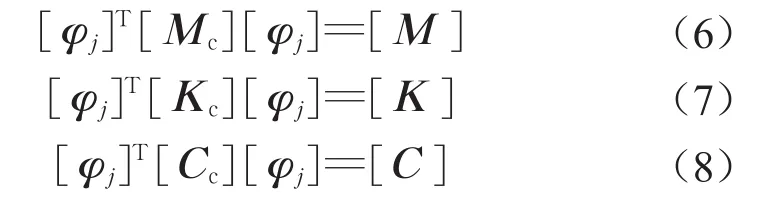
则式(2)可写为
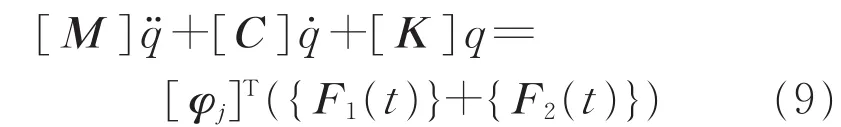
将式(5)代入式(3)、(9),得到
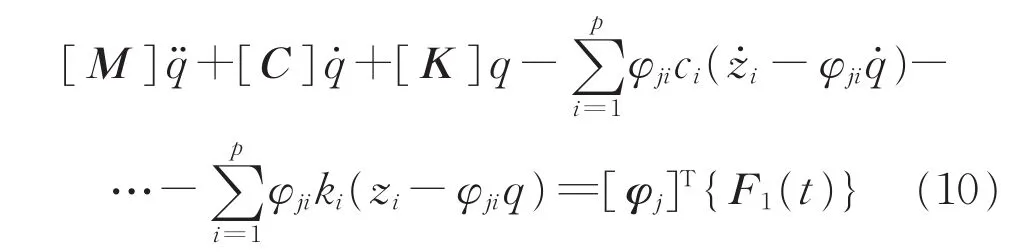
由式(1)可知
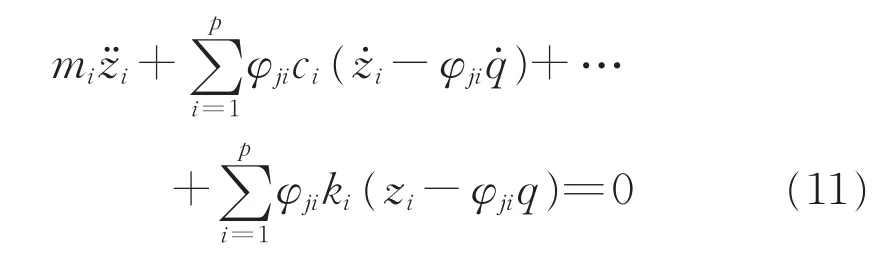
联立式(10)、(11),可得到地板与p个动力吸振器构成的新系统振动方程为
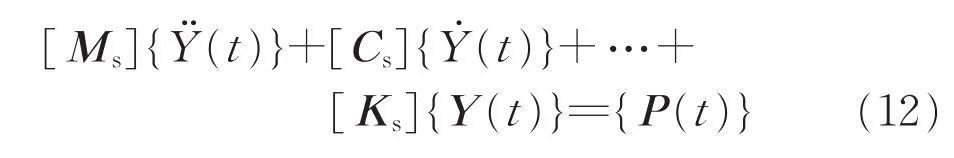
式中:

令 {F1(t)}={Fm}e-jωt,其中 {Fm}为各激励幅值组成的列向量,则
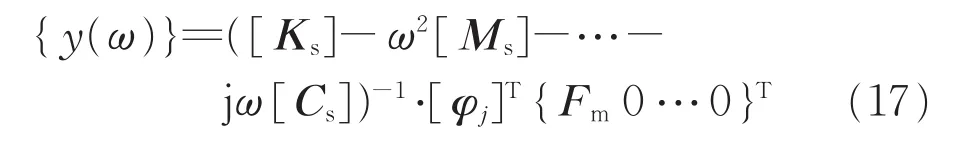
式中:q(ω)为{y(ω)}的第一列元素。对式(17)进行整理可得被控振型的模态坐标为

3 多重动力吸振器优化设计
3.1 动力吸振器参数优化设计
动力吸振器用于地板减振时,需要经过参数优化调谐才能有最优的减振效果[11-12]。为便于实际应用,本文令各动力吸振器采用相同的质量和阻尼比,则第i个动力吸振器的参数有
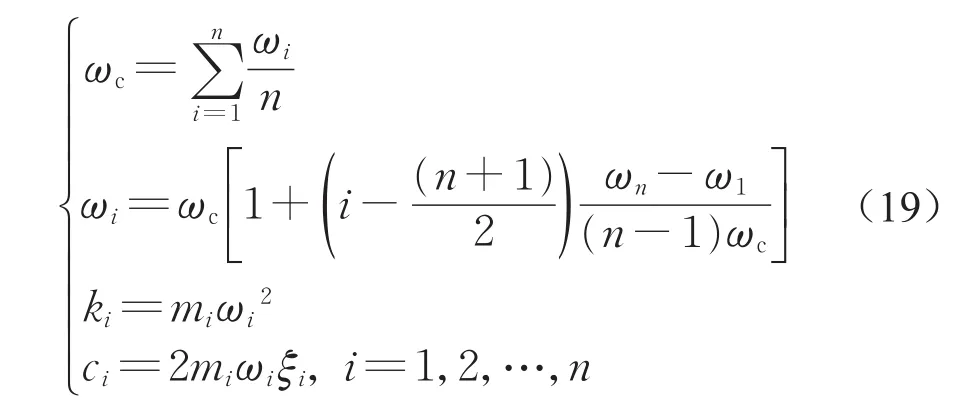
式中:ωc为结构振动受控振型的频率,同时是动力吸振器设计的中心频率;ξi为第i个动力吸振器的阻尼比。
令
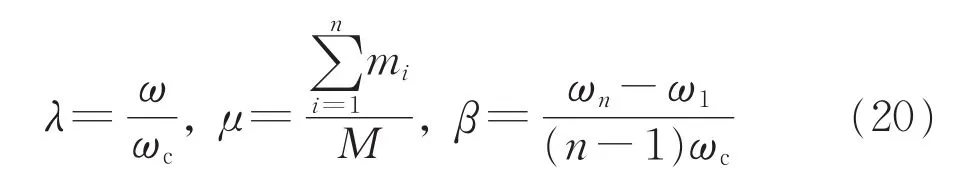
将上述参数代入式(18),整理得系统的模态坐标为
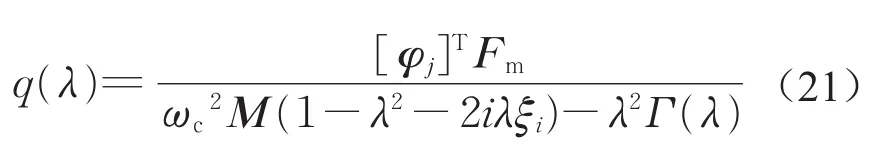
其中
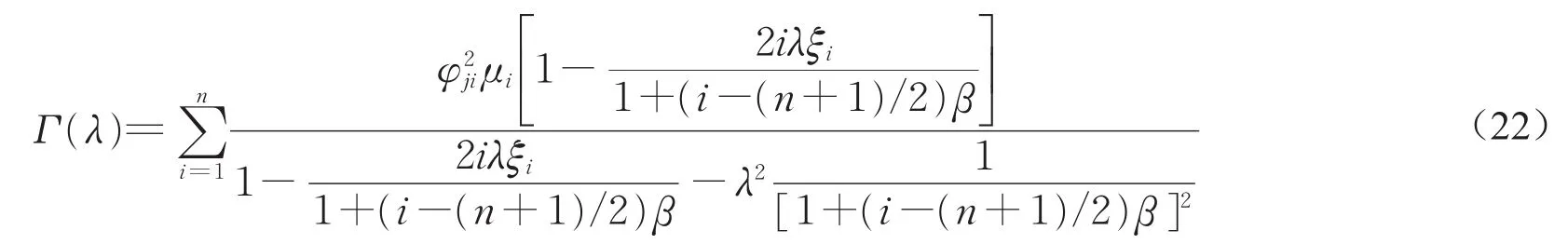
式(21)中q(λ)为包含动力吸振器参数的模态坐标,设计动力吸振器时通过寻找使q(λ)最小时各个动力吸振器参数,从而使系统的响应x最小。但在实际应用时该问题是关于q(λ)的多参数优化问题,无法直接获得解析解。因此,本文借助有限元分析方法,通过建立车辆有限元模型,上述优化问题可以转化为如下表达式:
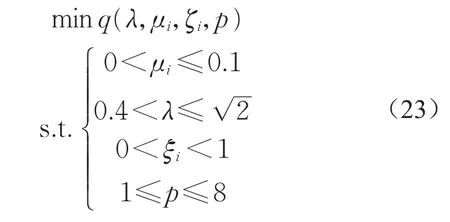
通过改变上述参数分析对地板振动响应的影响,寻找动力吸振器最优参数。
3.2 动力吸振器最优安装位置
由式(21)可知,当动力吸振器安装于不同位置时,对应的模态振型φji会发生变化,继而影响吸振器控制效果,因此首先需要确定吸振器的最佳安装位置。为研究动力吸振器安装位置对地板振动的影响,采用单个动力吸振器,分析相同参数时同一动力吸振器在不同位置对地板中部振动幅值的影响[10]。
根据式(21),当吸振器安装处的振型存在无穷大时,地板振动的模态坐标存在最小值
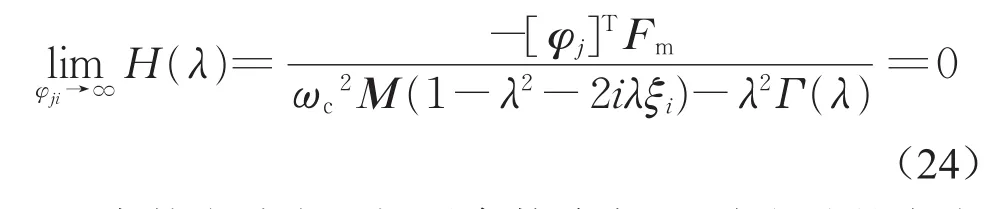
当某个动力吸振器参数确定后,式(21)的大小由安装位置所在的模态振型φji决定,且当φji取得最大值时,模态坐标q(λ)存在最小值,此时该阶模态对系统的响应贡献减少,系统的响应取得最小值。
4 多重动力吸振器对地板振动控制效果研究
4.1 包含地板的精细化车体有限元建模
为了验证上述多重动力吸振器对地板振动的控制效果,根据试验模型相关参数建立精细化仿真模型。在建立仿真模型时采用超弹性材料模拟橡胶地板支撑装置,地板阻尼采用结构阻尼等效代替。根据车体三维模型,采用壳单元及六面体单元对模型进行离散,建立包含地板的整备状态车体精细化有限元模型。其中,车体采用铝合金型材,车体中部下方包含了一个弹性吊挂设备,此外,还详细考虑了地板铝蜂窝结构(各项异性材料)、地板弹性支撑。所建立的有限元模型如图3所示,共包含631 657个单元,729 410个节点[13]。

图3 包含地板支撑装置的有限元模型Fig.3 Finite element model of carbody and floor
由于车体的振动响应由车体的主要模态叠加而成,为了保证仿真计算模态与试验模态接近,对建立后的仿真模型与试验模型的主要模态进行验证,结果如表1所示。从结果中可以看出,仿真结果与试验结果最大误差为3.75%,属于可接受的范围。
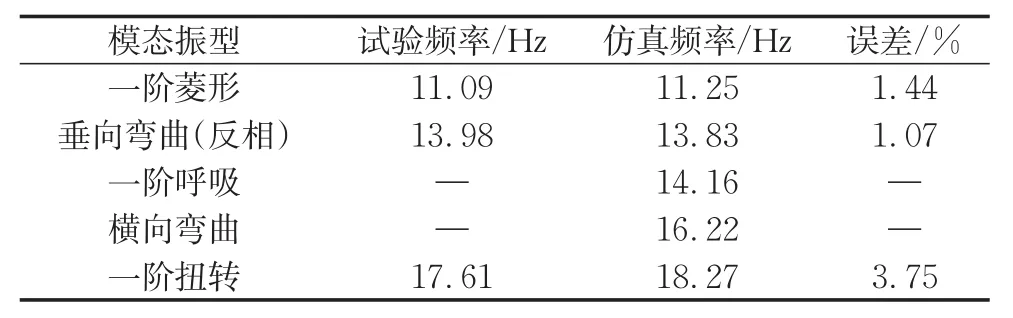
表1 仿真模态与试验模态误差对比Tab.1 Modal test and simulation results of car body and floor
计算包含地板的车辆模态,获得33.6 Hz模态时地板中部该阶模态振型向量中的最大值φji,代入式(23),即得到模态坐标q(λ)仅关于λ、μi、ζi、p的多项式,采用文献[14-15]中的优化算法寻找最小值,即可获得动力吸振器的最优参数。
4.2 吸振器最优安装位置
为确定不同安装位置对地板振动的控制效果,以单个动力吸振器为例,对比分析动力吸振器安装于振型最大处及其他位置时,地板中部振动的加速度传递率变化情况。
如图4所示,以二位端转向架中心作为起点(0L),振型最大处作为终点(1L),按照0.25L的间距研究每个点安装单个动力吸振器时对振动加速度的影响,其中L为转向架空簧中心到振型最大位置的直线距离[16]。各个动力吸振器的参数如表2所示,为了对比分析位置对控制效果的影响,每个动力吸振器具有相同的参数。

表2 动力吸振器最优安装位置时各吸振器参数Tab.2 Parameters of each DVA at optimized point
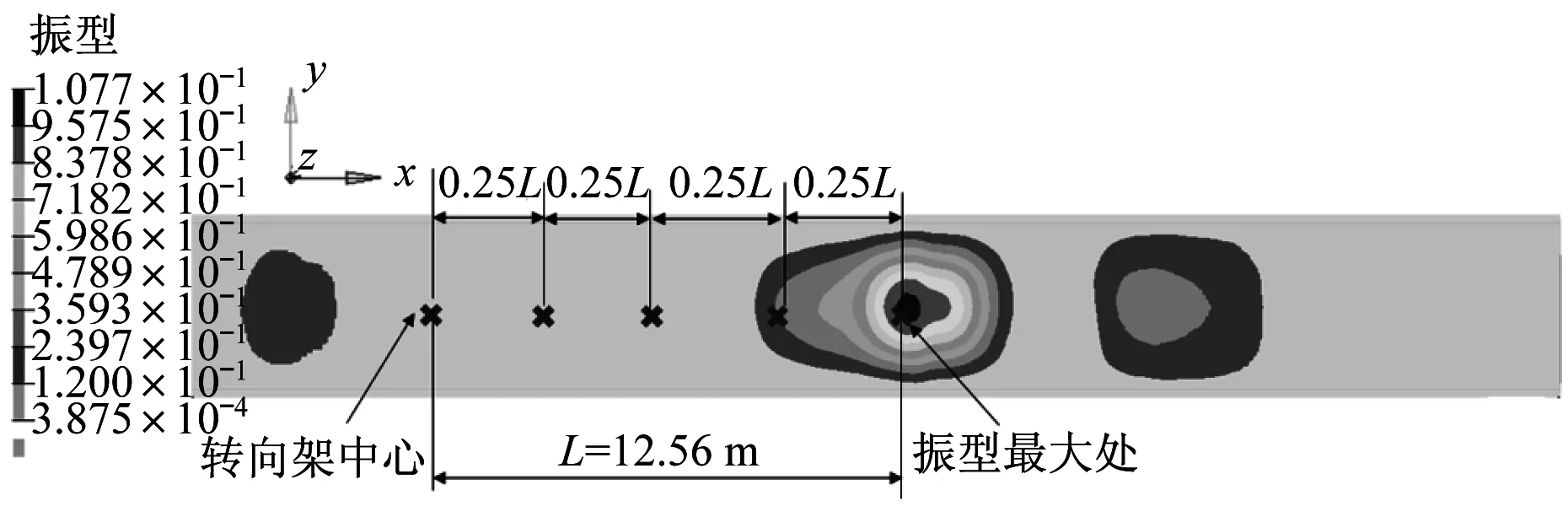
图4 动力吸振器布置位置示意图Fig.4 Schematic diagram of installing dynamicvibration absorbers in different positions
图5为动力吸振器安装于不同位置时,地板中部振动加速度的变化情况。当动力吸振器在振型最大处(L处)时,动力吸振器对振动的抑制效果最明显,地板中部的振动加速度与未安装动力吸振器相比在30~40 Hz明显下降;当动力吸振器安装于距离转向架中心0.75L处,地板中部在30~40 Hz振动略低于安装于振型最大处时,且振动的峰值向左略微发生偏移,这是由于0.75L处的振型小于L处,且安装的位置发生改变导致的。而0.50L、0.25L、0L处的振型(0.003 8)远小于振型最大处(1.07),安装在这些位置的动力吸振器对地板中部的振动加速度影响非常微弱。表明动力吸振器对地板振动贡献较大的模态产生的抑制作用较小。因此,应尽量保证每个动力吸振器的安装位置靠近地板振型最大处。
4.3 吸振器数量
单个动力吸振器可以衰减地板在指定频率下的振动,但轨道车辆在实际运行中,轨道传递至车体的激励频率随着运行速度不断发生变化,输入至车体的激励频率也随之变化,导致地板的振动从单频振动过渡至宽频振动,从而削弱单个动力吸振器控制效果。而多重动力吸振器能够将控制频率范围拓宽,增强系统对激励频率发生变化或吸振器参数不稳定时的适应性。为此分别计算了不同数量下的动力吸振器参数,为了便于比较动力吸振器数量对地板振动的影响,假定所有吸振器具有相同的质量比。
图6为当动力吸振器具有相同的质量比0.001时,动力吸振器安装在图4所示的振型最大处,地板中部的振动加速度随动力吸振器数量的变化情况。从图6可以看出,当质量比相同时,随着吸振器数量的增加,地板中部振动加速度逐渐减小,当吸振器数量n>4时,幅值的变化逐渐减弱,与未安装动力吸振器相比下降36%。当吸振器的数量n>6时,峰值下降40%,30~40 Hz的波峰接近,但被控地板频率范围逐渐变宽。
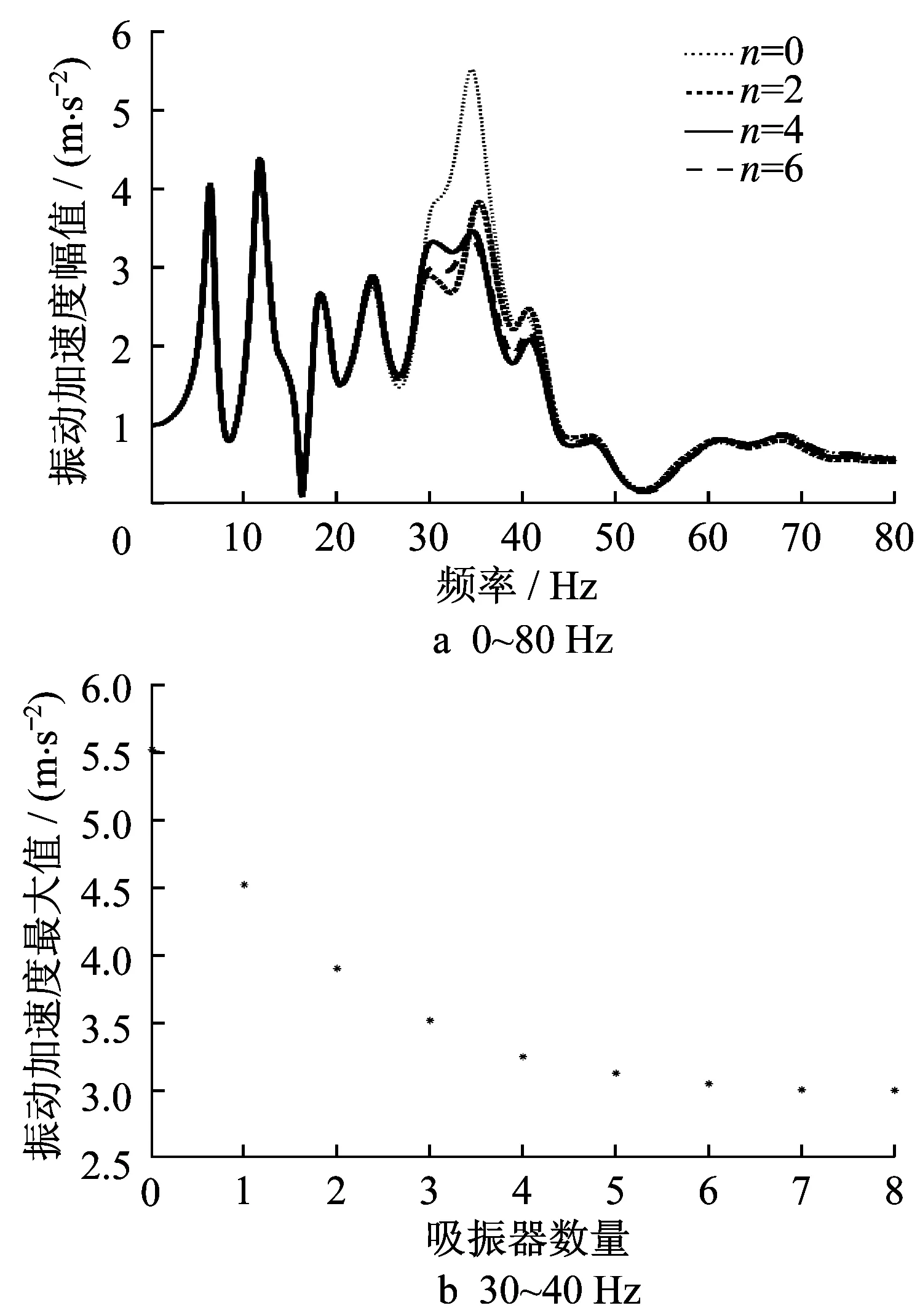
图6 动力吸振器安装数量对地板中部振动加速度的影响Fig.6 Effect of number of absorber on acceleration vibration
从吸振器的数量分析结果可知,吸振器的数量在一定范围内对地板振动响应的峰值衰减较为明显,而当吸振器数量增加时衰减效果不再线性增加,吸振器数量的增加对振幅衰减效果不再敏感。与此同时,吸振器数量的增加为地板振动控制提供了更宽的频率控制区间。因此,动力吸振器的数量与地板被控制频率范围相关,需根据实际工程要求选择。
4.4 吸振器质量比
受限于整车质量控制及安装空间限制,动力吸振器的质量不可能无限增加,且不同的质量比会影响吸振器其他参数的限制。采用控制变量法分别研究质量比μ、阻尼比ζi的变化与地板振动控制效果的关系。
图7为不同吸振器数量下80 Hz以内地板中部振动加速度最大值随质量比μ变化情况,当动力吸振器质量比在0.004以内变化时,幅值响应快速下降,超出0.04后仍有减小趋势,但衰减速度变缓。
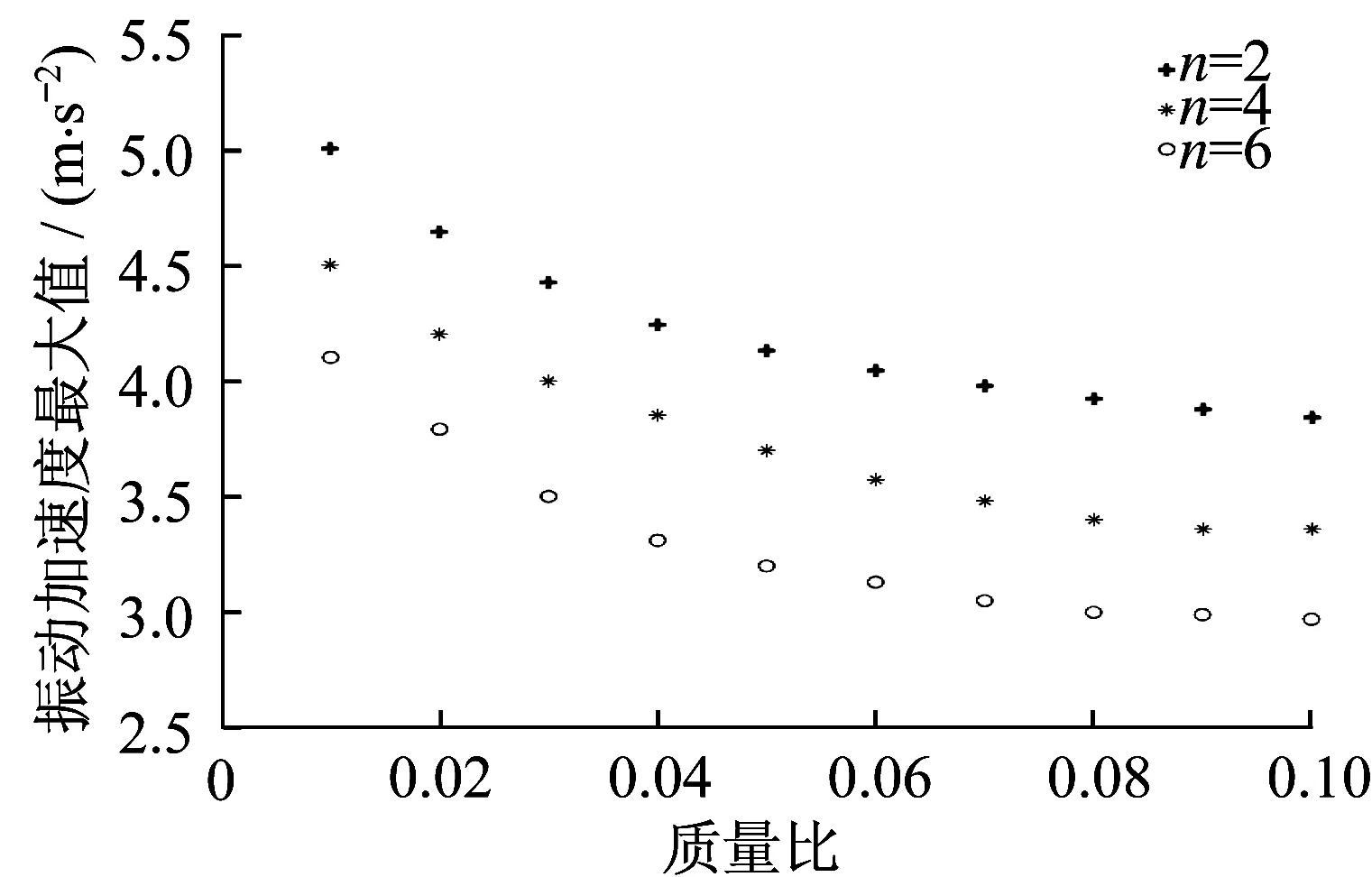
图7 动力吸振器质量比对地板振动加速度影响(30~40 Hz)Fig.7 Influence of mass ratio on vibration acceleration(30~40 Hz)
图8为质量比增加时,地板中部振动加速度的变化。质量比μ增加时,30~40 Hz的振动逐渐衰减,当质量比增加到0.004时地板的振动峰值逐渐平稳,质量比的增加对提升振动控制效果不再明显,吸振器质量的增加只对30~40 Hz频段产生影响。这是由于动力吸振器在设计时选择模态贡献量大的主导模态作为被控制模态,动力吸振器质量在增加的同时系统质量也在增加,因此地板中部在30~40 Hz之间的响应与质量比并非线性关系。从质量比对地板响应的变化结果可知,单个动力吸振器质量比在初始增加时能够有效降低目标峰值处的振动加速度,但是与数量变化相似质量比的增加不是无限制的,在质量比增加到一定程度后,增加质量比对振动峰值的影响较小。同时,质量比的增加对地板响应的峰值区间未产生影响。
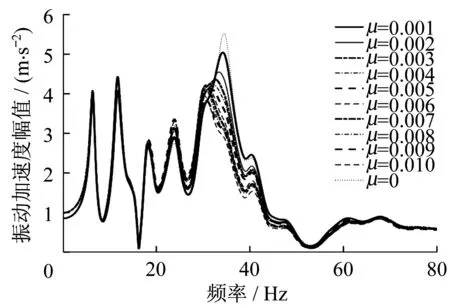
图8 n=2时,地板中部振动加速度随质量比变化Fig.8 Influence of mass ratio on vibration acceleration when the number of dynamic vibration absorbers is 2
4.5 吸振器阻尼比
以质量比为0.1的单个吸振器为研究对象,考虑阻尼比从0~0.14变化对地板振动、吸振器自身振动的影响,如图9所示。图中曲线表明,30~40 Hz区间内的地板响应最大值随动力吸振器的阻尼比增大而线性增大,而动力吸振器的响应随阻尼比增大而减小。这是由于动力吸振器阻尼比的增大会导致动力吸振器本身振动减小,从而削弱动力吸振器对地板振动的抑制作用。因此,从振动控制角度而言,动力吸振器的阻尼应取较小值。但是,当动力吸振器的阻尼比过小时,动力吸振器本身的振动无法得到抑制,因此动力吸振器需要具有一定的阻尼且不宜过大。
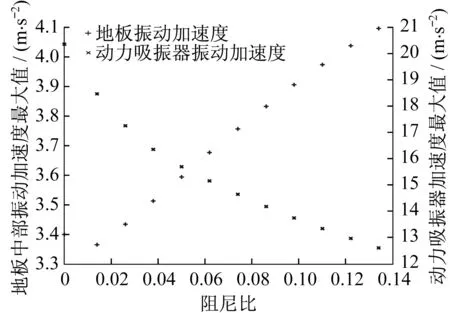
图9 动力吸振器阻尼对地板、吸振器振动加速度的影响(30~40 Hz)Fig.9 Influence of damping of dynamic vibration absorber on vibration acceleration of floor and vibration absorber(30~40 Hz)
上述分析表明,针对高速列车地板振动的动力吸振器设计,需要将动力吸振器安装在地板靠近模态振型最大处,动力吸振器的数量增加会拓宽频率控制范围,在一定程度上避免激励频率或系统本身原因对控制的影响。吸振器的质量比增加可以有效提高振动衰减性能,但系统总质量也有所增加使得吸振器的制振效果得到衰减。吸振器阻尼会削弱动力吸振器的控制效果,但在动力吸振器中加入一定阻尼可以保证吸振器在运用时吸振器的运动不会与地板发生干涉,而削减吸振器的位移。
4.6 多重动力吸振器对地板振动效果分析
针对本文研究的某高速动车组存在地板异常振动现象,根据地板振动测试结果(图1),地板异常振动峰值出现频率区间为30~40 Hz,因此选择峰值33.6 Hz对应的地板模态作为被控制模态,分析各个动力吸振器的参数如表3所示。
按照表3中计算的动力吸振器参数,在模型中建立动力吸振器,并以实测空气弹簧激励作为输入,计算车体地板中部在不同时刻的响应,如图10所示。从图10可以看出,对比无动力吸振器,采用多重动力吸振器后振动时域峰值明显降低,最大峰值响应下降约66%。
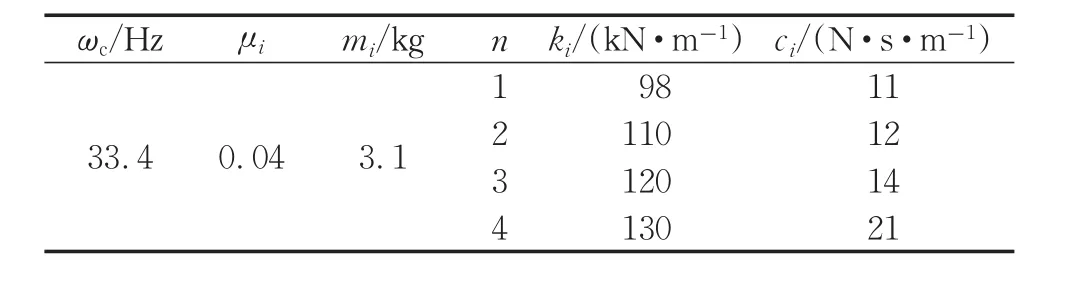
表3 动力吸振器参数Tab.3 Optimized parameters of MDVAs
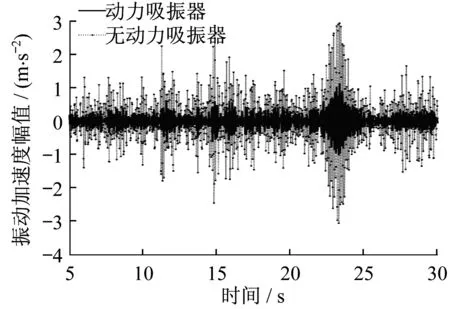
图10 采用动力吸振器前后车体中部振动加速度时域对比Fig.10 Response of vibration acceleration in the middle of the floor with MDVAs in time domain
为综合评价安装前后地板中部振动舒适度的变化,采用UIC舒适度指标进行衡量,结果如图11所示。可以看出,加入动力吸振器后地板中部振动舒适度指标降低0.3,为中等舒适。
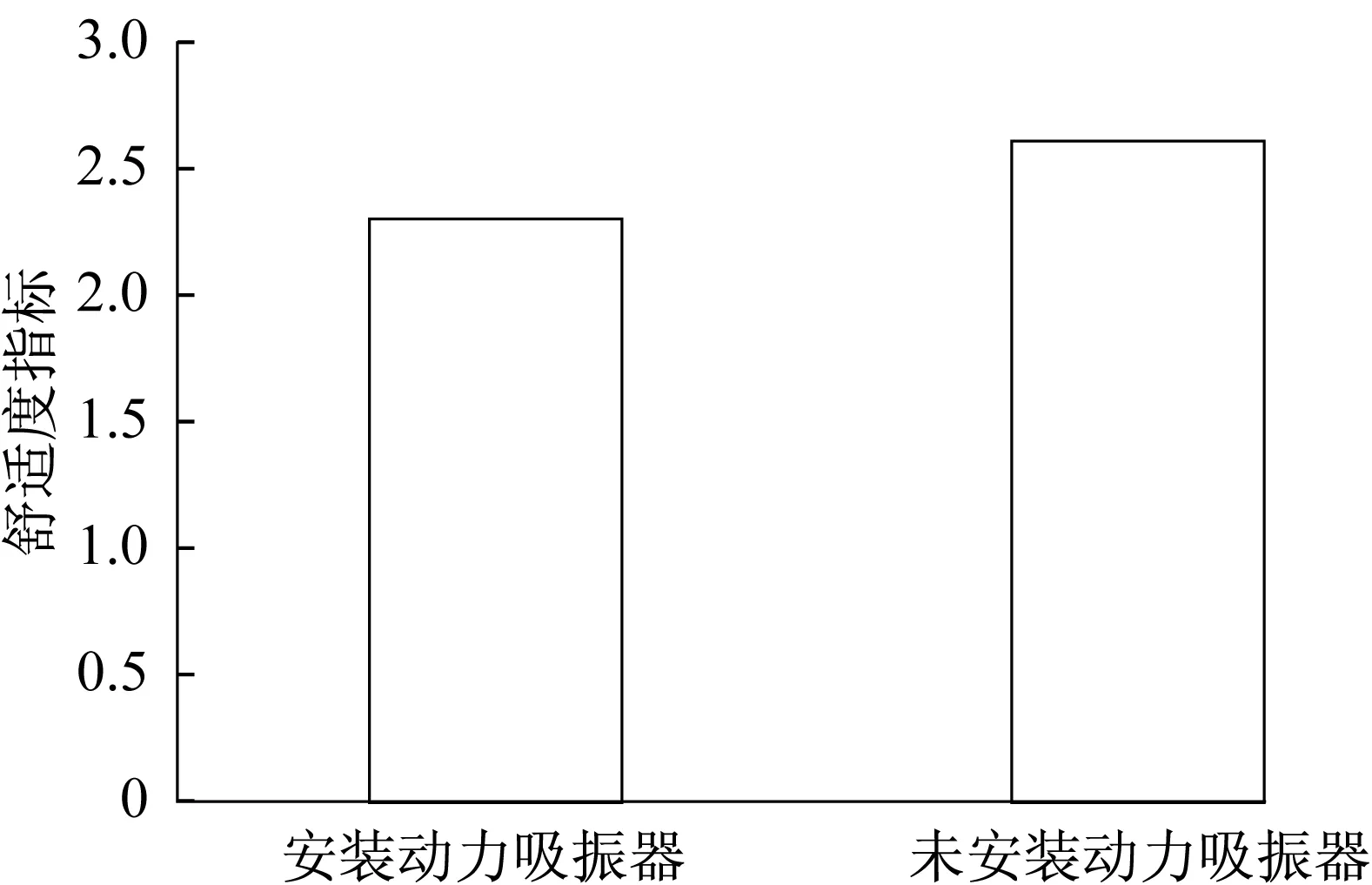
图11 采用动力吸振器前、后车体中部舒适度对比Fig.11 Comparison of comfort index in the middle of the floor after using dynamic vibration absorber
5 结论
本文从多自由度结构振动角度出发,建立了包含多个动力吸振器的高速列车车体地板振动离散模型,模型中考虑了多重动力吸振器安装位置、数量等参数,推导得到了用于控制地板振动的多重动力吸振器优化表达式。
采用实际发生异常振动的车辆参数建立了包含地板隔振装置的精细化模型,基于该模型对动力吸振器最优参数进行了验证。结果表明,安装位置会对控制效果产生明显影响,应尽量选择振型最大处安装,吸振器参数对控制效果的影响有限,不会随参数变化无限增加。
将本文计算的最优多重动力吸振器参数运用到模型中,结果表明在车辆试验激励下地板时域最大峰值下降约66%,同时车体中部测点车辆舒适度指标降低0.3。
