柱面网壳地震位移需求计算的迭代等效推覆方法
2020-06-16黄青隆罗永峰朱钊辰
黄青隆,罗永峰,曲 扬,朱钊辰
(1.同济大学 土木工程学院,上海 200092;2.中建五局土木工程有限公司,湖南 长沙 410004)
柱面网壳作为广泛应用的典型空间结构形式之一,其自由度数多、振型分布密集,结构地震反应较为复杂。确定柱面网壳的地震需求,是该类结构抗震设计、抗震性能评估的重要一环[1]。目前,结构的地震反应可用非线性时程分析法(response history analysis,RHA)准确计算,但该方法计算量大、耗时较多。推覆分析是另一种常用的地震反应分析方法。传统的推覆方法根据结构的基底剪力-顶点侧移关系,构造等效单自由度体系(equivalent singledegree-of-freedom system,ESDF),并确定其在地震作用下的目标位移,将目标位移对应的结构反应作为最终结果[2]。由于推覆分析方法效率高、精度满足工程要求,在多高层结构地震反应分析的应用日趋成熟[3]。而对于动力特性与多高层结构不同的空间结构,如柱面网壳,直接沿用传统的推覆方法计算该类结构的地震反应时还存在很多问题。
首先,空间结构的顶点往往并非结构地震反应的特征点,同时,基底剪力-顶点侧移的关系曲线不能反映结构的竖向变形贡献,致使采用传统方法构造的ESDF体系无法准确反映空间结构的抗震性能。为改进这一不足,多种基于能量的ESDF体系建立方法被提出[4]。Xiang等[5]从能量角度推导建立基于整体刚度参数的ESDF体系,并将其用于空间结构的推覆分析。算例结果表明,基于能量的ESDF体系可有效反映空间结构的抗震性能,但该类ESDF体系的荷载-位移(F-D)曲线往往需要借助中间参数或采用增量格式逐步叠加获得,当需要建立多个ESDF体系时,此类构造方法效率有待提高。
其次,在确定ESDF体系的目标位移时,为避免求解复杂非线性体系的时程响应,一般根据等能量原则将ESDF体系的F-D曲线等效为双折线[6]或多折线[7],再对简化体系进行求解。本质上,等能量原则已表明由此构造的简化体系与原体系的耗能仅在某等效点处相等,当简化体系的目标位移与等效点位移不重合时,二者的耗能不同,这一差别必然造成对目标位移、结构反应的预测偏差。此外,对于刚度较大的空间结构,其F-D曲线后屈服段较短[8],对于较柔的空间结构,其F-D曲线的屈服过程较长,二者的屈服点和双折线特征不明显,采用双折线化的FD曲线预测目标位移时该偏差可能进一步加大。
最后,目前应用于空间结构的推覆分析方法对单阶振型主导的结构预测精度较好,当结构的高阶振型效应显著时,该方法精度有所降低[5]。而空间结构的振型分布密集、质量参与系数累积较慢[9],根据质量参与系数累积值确定参与振型易导致选取的振型数量过多、计算耗时增加[10]。因此,对空间结构的推覆分析应考虑高阶振型影响,同时,应采用振型遴选方法识别主振型,以兼顾精度和效率。
鉴于此,本文以柱面网壳为研究对象,从能量等效角度推导建立了全量格式的ESDF体系F-D曲线。根据等能量原则,提出迭代等效方法用于计算ESDF体系的目标位移。最后,采用振型遴选方法选取主振型,结合完全二次项平方根方法(CQC)组合各主振型的响应,得到总体地震需求。建立两种典型边界条件的柱面网壳,验证该方法对于计算柱面网壳地震需求的有效性。
1 全量格式的能量等效ESDF体系
采用单调递增的模态荷载模式Mφn对结构进行静力非线性分析,其中,M、φn分别为质量矩阵和第n阶振型向量。第l荷载步的荷载向量Fn,l和对应的位移向量dn,l可写为
式中:χl为第l荷载步的荷载因子;qi,l为第l荷载步的第i阶振型位移。
易知,当结构响应进入弹塑性阶段,位移向量dn,l将包含多阶振型变形。在第l荷载步,荷载做功增量ΔWl为

注意到在以第n阶模态荷载为荷载模式进行推覆时,由于振型的正交性,推覆荷载仅对第n阶振型位移做功,因此式(2)可简化为

由于振型位移qn依赖于振型向量的量纲一化方式,不妨对qn做如下处理:

式中:Dn,l为不依赖于振型向量量纲一化方式的振型位移;Γn为在地震激励方向上的第n阶振型参与系数。
将式(4)代入式(3),进一步化简可得
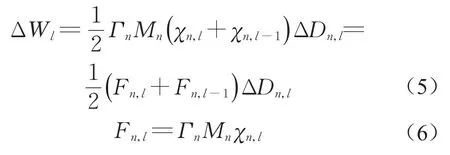
式中:Fn,l为第l荷载步的等效力。
若将Fn,l和Dn,l视为ESDF体系的等效力和等效位移,则式(5)表明,对任一荷载步,结构外力做的功与等效力在具有Fn-Dn关系的ESDF体系上做的功相等。其中,各荷载步的等效力可由式(6)直接求得。
结合式(6),式(4)可进一步改写为
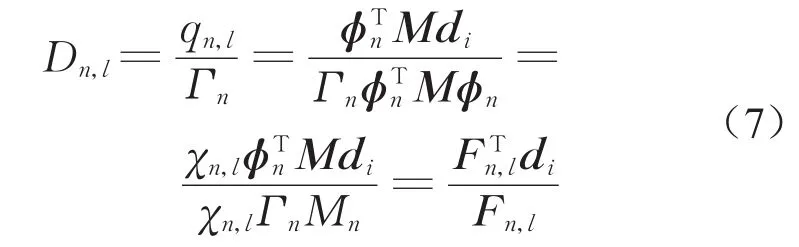
式(7)表明,每一荷载步等效体系的等效位移Dn,l可根据整体结构在该荷载步的荷载向量、位移向量和等效力求得。至此,该等效体系在各荷载步的等效力Fn和等效位移Dn均可由对应荷载步整体结构的计算结果直接求得,该过程不依赖中间参数,亦无需采用增量表达式进行逐步叠加计算。
等效体系的等效质量meq可按如下方法确定。设在第l荷载步下等效体系处于线弹性阶段,易知,等效体系的频率与结构第n阶频率相等,则有关系式
式中:ωn为第n阶振型频率。则等效质量meq为
需要说明的是,由推导过程可知,该等效体系的构造与地震动激励方向无关,即对于各向地震动输入,通过式(6)和式(7)均可构造相应的模态ESDF体系。特别地,当地震激励为水平x向时,有
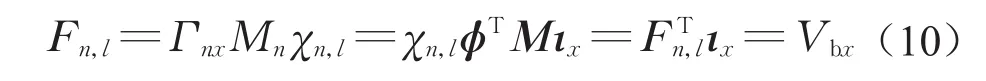
式中:ιx为x向单位方向向量;Vbx为结构x向基底剪力。

此时等效体系的等效力与结构的基底剪力相等,等效质量为结构的第n阶有效振型质量。而当地震动输入为其他方向时,该等效荷载不等于结构基底剪力,等效质量也与有效振型质量不同。
2 基于迭代等效的目标位移计算方法
理论上,地震作用下各ESDF体系的目标位移可采用非线性时程分析计算其峰值响应并进行估计,在实际计算中,为避免复杂非线性体系的时程计算,往往将等效体系中原始的F-D曲线理想化为双折线或多折线模型,再借助非弹性谱或时程分析方法计算该简化体系的峰值响应。显然,对原曲线的理想化处理提高了计算效率,但其计算精度将受到影响。
以经典的双折线等效为例,如图1所示,双折线等效一般以F-D曲线的荷载极值点P1为终点,根据双折线和原曲线所围面积A1与A2相等的“等能量原则”,按下式确定屈服位移Dy和后屈服刚度系数α:

式中:K0为曲线初始斜率;Fu为原曲线的荷载峰值;Du为峰值点对应位移。根据Dy和K0可计算得到体系的等效屈服荷载Fy。
双折线模型可由屈服位移Dy和后屈服刚度系数α确定。易知,由此确定的双折线和原曲线在曲线终点处保持相同的耗能、位移D和作用外力F等状态,但二者在曲线非线性段其余点处的状态并不相同,这一差别将造成采用简化体系预测的结果存在偏差。当原体系的F-D曲线无明显的双折线特点时,该处理方法可能造成双折线和原曲线相差较大,即A1与A2之和较大,导致二者在曲线非线性段上各点耗能的差异进一步加大。

图1 ESDF体系F-D曲线的双折线等效示意图Fig.1 Bilinear equivalent F-D curve of ESDF system
实际上,预测ESDF体系目标位移的合理简化模型,应具备两个特征:一是简化折线与原曲线应尽可能贴合,以减小各点耗能差异;二是简化体系的峰值响应点与原体系的峰值响应点重合,即保证二者的峰值响应点具有相同的耗能、位移和等效外力。
注意到当原始体系的峰值响应为Dpeak(Dpeak<Du)时,实际上体系的响应点仅分布于[0,Dpeak]区间,因此可仅对原曲线的[0,Dpeak]段按式(12)~(13)建立双折线简化体系。易知在[0,Dpeak]段,该体系显然比以Du为终点等效的简化体系更贴近原曲线。若简化体系的峰值响应同样为Dpeak,则表明该简化体系与原始体系的峰值响应点相同,可将该简化体系作为最终简化体系,以该体系的峰值响应作为目标位移。
由于原始体系的峰值响应未知待求,最终简化体系可借助迭代等效方法确定。迭代等效方法的示意图如图2所示,具体计算步骤如下:

图2 ESDF体系F-D曲线的迭代等效示意图Fig.2 Iterative equivalent F-D curve of ESDF system
首先,假定原F-D曲线的初始峰值响应点为荷载峰值点P1,P1处位移为Du,1,以P1为终点进行双折线等效可得双折线模型L1,设按此模型计算得到峰值响应点B1处位移为Dpeak,1。若Du,1和Dpeak,1满足式(14)的容差要求,则认为L1的峰值响应点与原体系的峰值响应点重合,停止计算,并将Dpeak,1作为该体系的目标位移;否则,以原曲线中位移Dpeak,1对应点P2为等效终点,再次进行双折线等效得到模型L2,并重复前文步骤,直至双折线模型的预测目标位移Dpeak,i与其等效终点的位移Du,i满足下式要求:
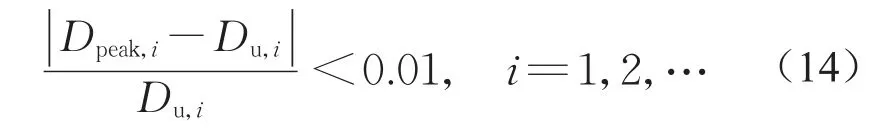
迭代等效方法保证了双折线模型与原模型在目标位移点处具有相同的耗能等状态,同时,以目标位移点为终点等效的双折线与原曲线更加贴合,减小了其余各点的耗能差异,因此,该方法较一次等效法可以得到更为准确的结果。式(14)设定了收敛阈值为0.01,在实际应用中,可根据精度要求微调该阈值以兼顾计算效率和精度。需要说明的是,尽管迭代等效方法增加了理想化模型的计算次数,但借助非弹性反应谱或时程分析法,依然可以方便地获取双折线模型的峰值响应,因此,总体上该方法的计算效率仍高于直接计算原始体系的峰值响应。
3 总体地震需求计算
3.1 主振型遴选
结构总体地震需求可由各等效单自由度体系目标位移处的响应组合而得。对于自由度数较多、振型分布密集的大跨度空间结构,如柱面网壳和球面网壳,事先遴选对结构反应贡献较大的振型有助于减少工作量,从而提高计算效率。
本文采用基于位移谱的振型遴选方法[10]遴选空间结构的主导振型。该方法可识别不同地震动激励下对位移反应贡献较大的主导振型。根据该方法,先将各振型按质量矩阵正则化处理,然后由式(15)计算其位移反应相对贡献值βn,将满足阈值βd要求的振型遴选为主振型。

式中:rn=ΓnSd,n,为第n阶振型的弹性峰值响应;Sd,n为第n阶振型的弹性位移谱谱值;βd为遴选阈值,表征主振型相对贡献值的下限,该阈值大小可根据精度要求设置。一般认为振型的相对贡献值相差两个数量级以上时,即阈值βd取为0.01时,相对贡献值较小的振型贡献可忽略不计。
3.2 计算流程
根据分析需要确定结构的需求指标。对于柱面网壳,常用需求指标为最大节点位移、总体位移包络、杆件轴力和结构损伤因子[1]等。由于位移指标宏观上体现了结构刚度的变化,表征了结构地震反应的强弱。因此,本文以位移指标作为柱面网壳的地震需求指标。按照振型遴选结果,依次建立各主振型的等效单自由度体系,将各等效体系目标位移处的反应加以组合,便可得到对总体地震需求的预测。
综合前文所述内容,基于迭代等效推覆的柱面网壳地震需求计算方法流程可总结如下:①模态分析——结构建模,获取结构的振型信息。②构造ESDF体系——根据式(15)遴选结构主振型,依次进行各主振型的模态推覆分析。根据第1节方法,将各推覆结果代入式(6)、(7)和(9),构造各主振型的ESDF体系。③确定目标位移——采用第2节方法,计算各主振型ESDF体系在地震作用下的目标位移。对于频率较大的高阶主振型,可预设其在地震作用下保持弹性,其峰值响应可由弹性反应谱直接计算,方法效率得以进一步优化。④预测总体需求——当结构响应仅由第n阶振型主导时,可参照传统的推覆方法,提取目标位移对应的荷载因子χn,peak,采用模态荷载χn,peakMφn推覆结构提取需求指标;当响应由多阶振型共同主导时,可采用CQC规则组合各主振型目标位移处的振型响应,进而得到总体地震需求。
4 算例分析
4.1 模型信息
分别建立无山墙和考虑山墙约束的两个单层柱面网壳模型。两个模型编号依次为C203A和C203B,结构布置如图3所示。两个柱面网壳几何形状相同,横向跨度均为20 m,矢跨比为1/3,纵向长度为36 m。如图3所示,C203A和C203B的纵向柱脚均采用三向铰接支座,此外,C203B在两端边跨杆件节点处增设竖向约束以考虑山墙对结构变形的约束作用。
采用有限元软件ANSYS进行分析,结构杆件采用梁单元Beam189模拟。杆件均为圆钢管,钢管截面如表1所示。考虑到C203A无山墙约束,故对其杆件进行加强以保证结构整体刚度满足承载要求。模型中的钢材密度为7 850 kg·m-3,材料特性采用文献[12]中的钢材试验拟合结果施加,其中弹性模量为2.06×105MPa,泊松比为0.3,屈服强度为235 MPa。在分析中,将结构承受的均布荷载(120 kg·m-2)等效为集中质量作用于结构各杆件交汇节点处,集中质量采用质量单元mass21模拟。

图3 模型结构布置Fig.3 Structural layouts of numerical models

表1 模型杆件截面表Tab.1 Member section information mm
4.2 模态分析
表2列出了各模型中具有较大x向质量参与系数βmass的前6阶振型信息。由表2可知,无山墙约束的模型C203A整体较柔,结构1阶振型周期为1.23 s,其βmass为64.52%。结构βmass较高的振型集中在低阶振型中(第1、5阶)。考虑山墙约束的模型C203B基本周期为0.55 s,由于该阶振型为对称振型,其x向βmass为0,故未将其列入表2。但由此可以看出,尽管C203B采用了较小的杆件型号,但其基本周期仍小于C203A,这表明山墙约束对于结构刚度有明显的增强作用,考虑山墙约束的网壳采用较少的钢材用量便可获取较大的结构刚度。考虑山墙约束后,βmass最大的振型为第3阶振型(60.61%),高阶振型中出现了βmass大于10%的振型(第166阶振型)。

表2 模态信息Tab.2 Modal information
4.3 地震波选取
选取中硬场地土和中软场地土的各16条地震波作为地震动激励,输入方向为x向。由于C203A周期较长,考虑地震动的不利作用,将中软场地土的地震波(S1~S16)作为C203A的地震动输入;相应地,将中硬场地土的地震波(F1~F16)作为C203B的地震动输入。各地震波的伪加速度as反应谱(取阻尼比ξ=0.02)绘于图4。为保证结构在地震作用下进入弹塑性,对C203A和C203B,将选用的地震波按各结构基本周期对应的伪加速度谱谱值分别调幅为1.0g和2.0g。
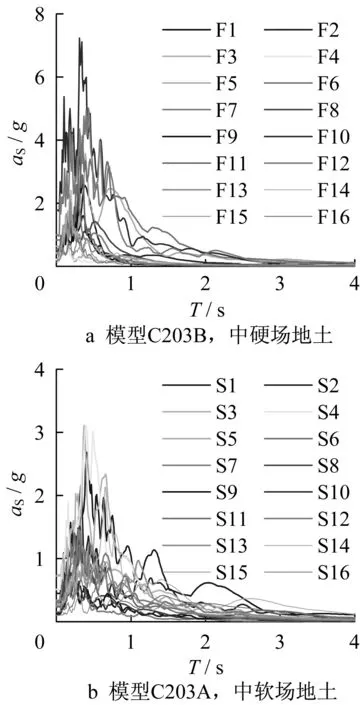
图4 地震动伪加速度反应谱Fig.4 Pseudo acceleration spectrums of seismic excitations
4.4 主振型ESDF体系
按第3节振型遴选方法,将各结构前200阶振型中位移响应相对贡献值βn大于0.01的主振型分布绘于图5。由图5可知,无山墙柱面网壳C203A的位移反应主要由基本振型贡献,存在少量高阶振型贡献值大于0.01,但该部分振型βn均小于0.1。与C203A不同,C203B的高贡献振型分布较为广泛。C203B的第2、3阶振型在各地震动作用下的相对贡献值均大于0.4,这表明这两阶振型将共同主导该网壳的位移反应。此外,结构的高阶振型在某些地震动下也将产生大于0.1的相对贡献值,这表明对于考虑山墙约束的柱面网壳,高阶振型贡献不可忽略。
本算例选取各结构中贡献较大的低阶振型建立非线性ESDF体系,即C203A中第1阶振型和C203B中第2、3阶振型。采用式(6)和式(7)计算的各ESDF体系F-D曲线及初始双折线等效曲线如图6所示。由图6可知,C203A的第1阶、C203B的第2阶ESDF体系的F-D曲线与初始等效曲线较为贴合,而在C203B的第3阶ESDF体系中,两条曲线所围面积较大,采用初始等效曲线预测目标位移可能产生较大误差。对于高于3阶的振型,由于其频率较高,可预设其在地震作用下保持弹性,可采用弹性反应谱计算其峰值响应。

图5 结构各振型的位移贡献相对值β nnFig.5 Modal relative contribution value of displacement β nn
4.5 计算结果分析
为验证本文提出的迭代等效方法、基于迭代等效的推覆方法的有效性,本节分别采用一次等效的单模态推覆(S_MPA)方法、迭代等效的单模态推覆(SI_MPA)方法和迭代等效的多模态推覆(MI_MPA)方法计算各模型的地震需求,并将各方法结果与RHA结果比较。需要说明的是,单模态推覆方法均以结构中βmass最大的振型建立ESDF体系,按文献[5]中的拓展模态推覆方法计算结构地震需求;在多模态推覆中,选取相对贡献值大于0.01的振型作为主振型,采用迭代等效方法依次计算各主振型ESDF体系的目标位移,然后,将各目标位移对应的总体振型反应采用CQC规则组合得到总体反应。以结构的地震位移需求为例,提取各方法计算结果中结构的最大节点位移和结构的整体位移包络值作为指标,用以比较各方法的预测精度。
4.5.1 最大节点位移
图7a给出了模型C203A在各地震动作用下x向和z向的最大节点位移,图中各虚线为误差标准线,节点位移的相对误差按下式计算:

式中:dRHA表示采用时程分析得到的最大节点位移;dMPA表示采用推覆方法得到的最大节点位移。
从图7a中可以看出,各推覆方法对C203A的各向最大节点位移预测误差均处于±10%范围内。与S_MPA相比,SI_MPA结果精度更高,这表明迭代等效方法可有效提高目标位移的预测精度。考虑高阶振型贡献的MI_MPA与SI_MPA的x向最大节点位移结果相近,而MI_MPA的z向最大节点位移结果相对偏小,但其相对误差仍处于±10%范围内。这表明对于单一振型控制的结构,采用基于迭代等效的单模态推覆即可得到较好的预测结果。
图7b为C203B最大节点位移结果对比。由图可知,基于一次等效的S_MPA高估了结构x向最大位移,同时低估了结构z向最大位移。相比S_MPA,SI_MPA对结构x向最大位移的大部分预测误差均处于±20%范围内,但该方法依然低估了结构z向最大位移。而MI_MPA对结构的x向、z向最大位移的大部分预测误差均处于±20%的范围内。这表明对于多振型主导的结构,各主振型的贡献不可忽略。
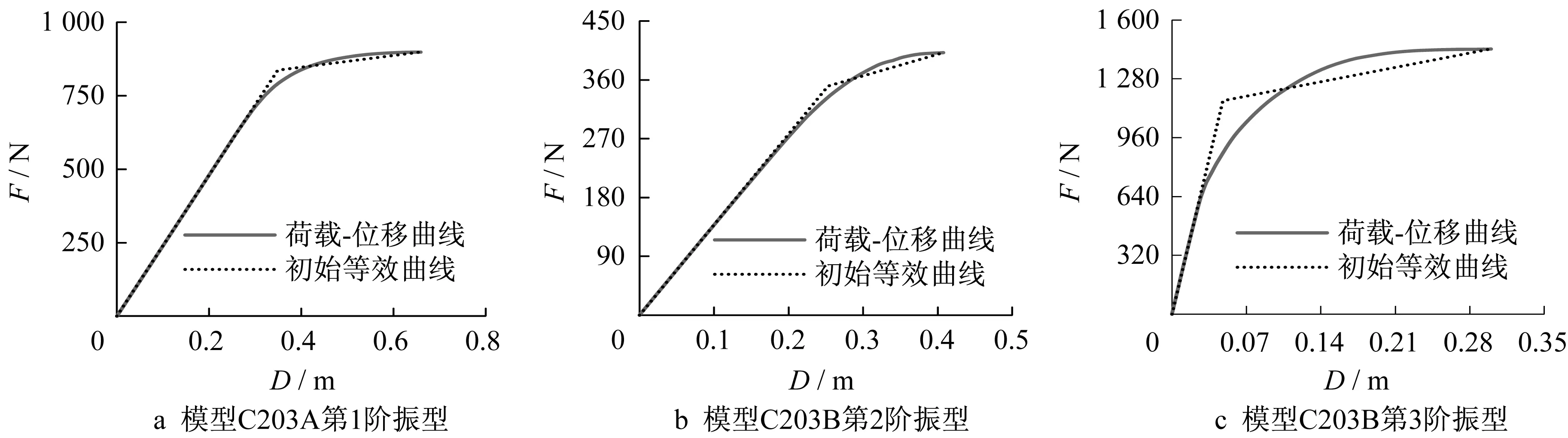
图6 各等效单自由度体系F-D曲线Fig.6 F-D curves of ESDF systems

图7 结构的x向、z向最大节点位移对比Fig.7 Comparison of maximum nodal displacements in x and z direction
表3给出了采用3种方法得到的各结构最大节点位移的误差统计。由表3可知,对于C203A,SI_MPA在x向、z向最大节点位移计算中均保持较低的平均误差(1.7%和1.0%),MI_MPA的x向平均误差较SI_MPA有所降低;其z向平均误差为-5.8%,尽管稍高于SI_MPA的z向平均误差,但仍处于合理的精度范围。相比基于迭代等效的推覆结果,基于一次等效的推覆结果在各向最大位移的平均误差均较大,这表明了迭代等效对于提高目标位移预测精度、减小推覆结果误差的有效性。对于地震反应由多振型主导的C203B,多模态推覆方法MI_MPA显示了其在x向、z向最大节点位移预测的适用性。相较单模态推覆,多模态推覆在x向、z向最大位移的平均误差分别为11.3%和-10.8%。对于不同边界条件的柱面网壳,多模态推覆方法的精度均保持稳定。
4.5.2 整体位移包络
结构的整体位移包络由各节点x向和z向位移峰值反应dx和dz组成,该指标反映了结构在地震作用下各点的位移需求。限于篇幅,仅在图8给出C203A在地震动S1输入下由各方法得到的包络结果,在图9绘出C203A在所有地震动输入下各点位移包络均值。从图中可以看出,C203A在地震作用下各向位移幅值较大的节点集中于网壳跨中两侧1/4跨度区域。各推覆方法得到的位移包络分布模式均与时程分析结果较为接近。

表3 结构最大节点位移误差εd统计表Tab.3 Error εdstatistic of maximum nodal displacement %

图8 模型C203A在S1作用下的各向整体位移包络Fig.8 Displacement envelope results of C203A in seismic excitation S1
采用各推覆方法计算得到的整体位移包络结果的总体偏差εtotal可采用下式计算:

式中:i为节点编号;N为结构的节点总数。
C203A偏差结果如图10所示。由图10可知,大部分情况下,S_MPA高估了C203A的各向位移包络,SI_MPA的预测精度较高,而MI_MPA对结构的z向位移包络稍有低估。对于x向位移包络,S_MPA、SI_MPA和MI_MPA的总体偏差平均值分别为6.5%、3.3%和3.4%;对于z向位移包络,三者的总体偏差均值依次为1.3%、-1.7%和-5.2%。对于主导振型单一的结构,3种方法均保持良好的预测精度。

图9 模型C203A的各向整体位移包络均值Fig.9 Average displacement envelope results of C203A
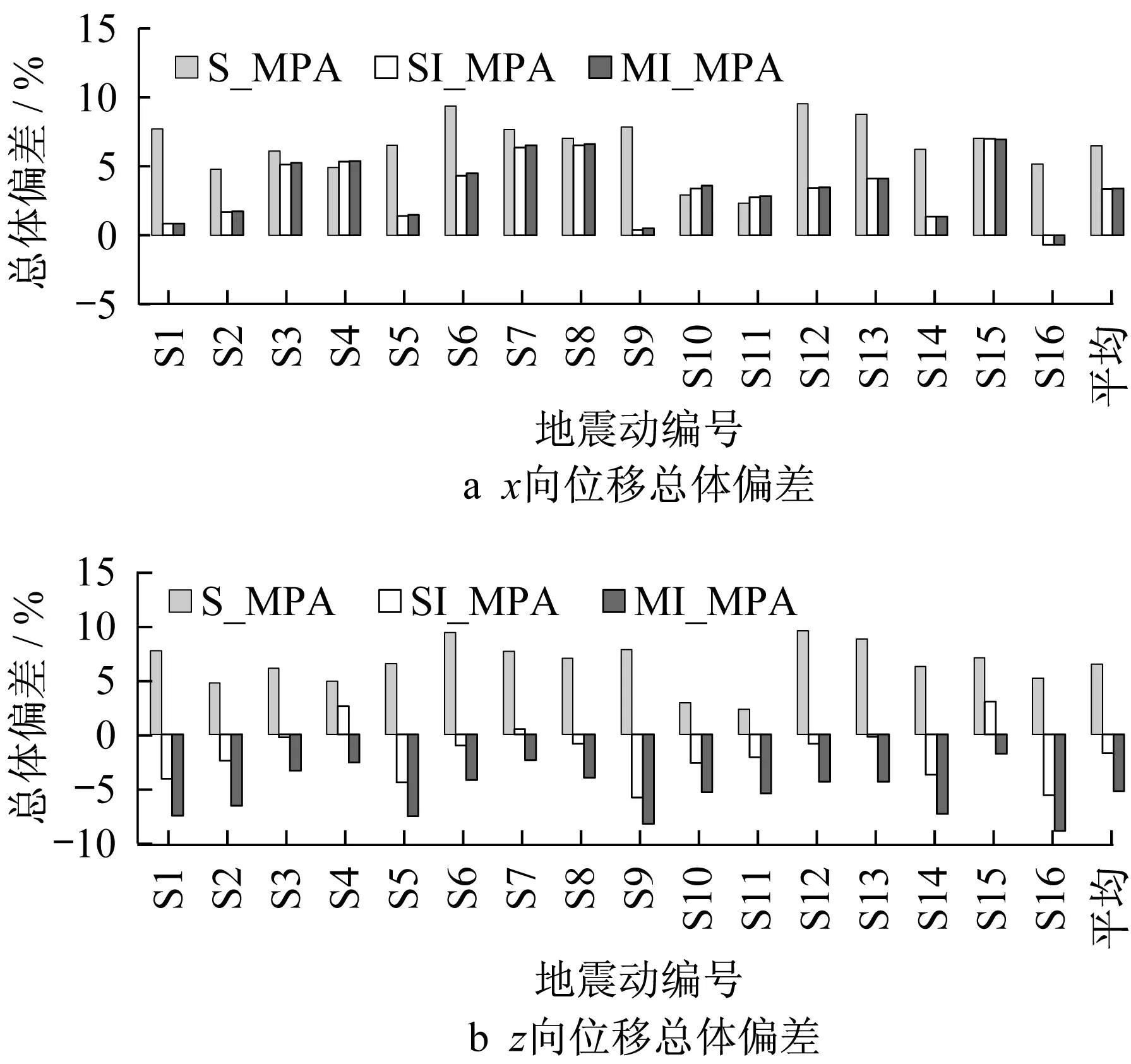
图10 模型C203A各向位移总体偏差Fig.10 Overall error statistics of nodal displacements in x and z direction of C203A
图11给出了C203B在地震动F6作用下各方法计算得到的位移包络结果。图12为C203B在所有地震动输入下各点位移包络的均值分布。由图可知,考虑山墙约束的柱面网壳位移分布模式有所改变。网壳的x向位移响应较大的节点集中于靠近纵边约束的支座附近,而z向位移响应较大的节点分布于网壳跨中两侧区域。对于x向位移包络,3种推覆方法得到的位移分布模式较为接近,但S_MPA显著高估了各点位移需求。基于迭代等效的推覆方法计算结果与时程分析结果较为接近。对于z向位移包络,单模态推覆方法无法准确预测其位移分布模式,而多模态推覆方法在位移分布模式以及位移幅值上均可给出较好预测。

图11 模型C203B在F6作用下的整体位移包络Fig.11 Displacement envelope results of C203B in seismic excitation F6

图12 模型C203B的整体位移包络均值Fig.12 Average displacement envelope results of C203B
各推覆方法对C203B的整体位移包络的总体偏差统计如图13所示。由图13可知,对于主导振型并不单一的结构,S_MPA高估了结构的各向位移包络;SI_MPA可准确与结构的x向位移包络,而其z向位移包络结果的总体偏差较大;MI_MPA对C203B的各向位移包络均可给出较好预测。对于x向位移包络,S_MPA、SI_MPA和MI_MPA的总体偏差平均值分别为10.2%、-3.2%和-4.0%;对于z向位移包络,三者的总体偏差均值依次为-14.6%、-20.3%和-0.9%。

图13 模型C203B各节点的各向位移总体偏差Fig.13 Overall error statistics of nodal displacements in x and z direction of C203B
5 结论
本文以柱面网壳为研究对象,从能量角度构建了全量格式的ESDF体系,提出迭代等效方法计算ESDF体系的目标位移,由此建立迭代等效推覆方法用于计算结构地震位移需求。根据数值算例计算结果,可得出以下结论:
(1)山墙约束对柱面网壳的动力特性影响较大。对于无山墙约束的柱面网壳,其地震位移反应主要由单阶振型主导;而考虑山墙约束后,柱面网壳的地震反应将由多阶振型共同主导。
(2)相比一次等效方法,迭代等效方法可有效提高ESDF体系目标位移的预测精度。
(3)当结构反应由单阶振型主导时,采用基于迭代等效的单模态推覆方法即可对地震位移需求做出较好的预测;当结构反应由多阶振型共同主导时,应采用基于迭代等效的多模态推覆方法预测结构的地震需求。
