电磁旋转涡流制动器制动力矩控制

2020-06-16张济民

同济大学学报（自然科学版） 2020年4期

张济民，任乔，张鹏

（同济大学铁道与城市轨道交通研究院，上海 201804）

随着高速铁路的发展，列车运行速度取得了显著提高。列车运行的安全性离不开制动系统的作用，对于高速运行的高速列车来说更是如此。在列车高速制动时，传统的摩擦制动存在磨耗快、噪音大等明显缺陷，而涡流制动作为一种非摩擦制动方式则可有效避免这些问题。按励磁类型来分，涡流制动分为电磁涡流制动和永磁涡流制动。对于电磁涡流制动而言，制动力矩同制动器的励磁电流密切相关。一般而言，一旦制动器完成在列车上的集成，除励磁电流之外，制动器的其余几何及电磁参数不再变化。当励磁电流一定时，由于列车的速度将随着制动的进行而减小，制动器输出的制动力矩也将发生变化，从而使得列车制动减速度产生波动。为了尽可能降低列车制动减速度的波动程度，应使制动器尽可能输出恒定的制动力矩。因此，需要为制动器设计合适的控制系统。

针对涡流制动器制动力矩的控制方法，众多学者从仿真和试验方面开展了研究工作。Ryoo等通过数值仿真，得到了制动器在不同励磁电流下的制动特性曲线，以此为基础，设计了一种以励磁电流为参考量的恒转矩控制算法，改善了制动器的制动性能，最后在司机驾驶模拟器上验证了该算法的实用性［1］。Lee等针对小比例汽车用电磁缓速器研究了滑模控制及鲁棒控制，通过仿真和试验对比发现，制动器在控制器作用下响应迅速［2］。邓妮针对TR08型高速磁悬浮列车，制定了基于模糊控制的紧急制动策略，控制器通过调节励磁电流的大小来改变制动器的制动力［3］。Anwar等采用开环控制策略对汽车用电磁缓速器制动力矩施加了控制，并将控制器应用在整车模型中考察汽车制动性能［4］。朱科采用PWM的方式来调节励磁电压，以控制涡流制动器的制动力［5］。以上研究表明：①获取制动特性曲线是研究涡流制动器制动力矩控制方法的前提；②由于制动特性曲线呈非线性，准确的数学模型难以建立，故现有控制策略较多采用模糊控制及滑模控制等非线性控制方法；③目前已有的制动力矩控制研究集中在汽车用缓速器及高速磁悬浮列车用线性涡流制动器上，而针对旋转涡流制动器的控制研究则较少涉及。

本文将以电磁旋转涡流制动器为控制对象，建立制动力矩控制系统模型，设计恒定期望制动力矩仿真工况和3种制动力矩控制算法，并对仿真结果进行对比分析。

1 电磁涡流制动器制动力矩建模

本文根据微分原理推导制动盘涡流、气隙磁场和涡流功率，其次从能量守恒定律出发，将涡流功率视为制动功率，最后根据功率与力矩的关系得到制动力矩。

1.1 模型假设

为便于制动力矩的推导，对模型作如下假设：①不考虑温度对制动盘材料电阻率ρ 的影响，即假定ρ为常数；②电磁铁产生的磁力线只穿过磁轭在制动盘上的投影区域；③制动盘材料各向同性，相对磁导率μr 处处相等；④不考虑电磁铁漏磁、磁饱和及磁滞效应。

1.2 涡流分析

单个磁轭在制动盘上的投影区域为一扇形，如图1所示。该扇形的内外半径分别为r1和r2，扇形覆盖的角度为40°。将该扇形看作由无数个宽度为dr的相似扇形环组成，这些扇形环的位置可由其内外圆弧到大扇形中间半径的距离r来表示，其中0≤r≤Δr，Δr=rc-r1=(r2-r1)/2，rc=(r1+r2)/2。

扇形环的周长Lr为

扇形环包围的内部扇形的面积Sr为

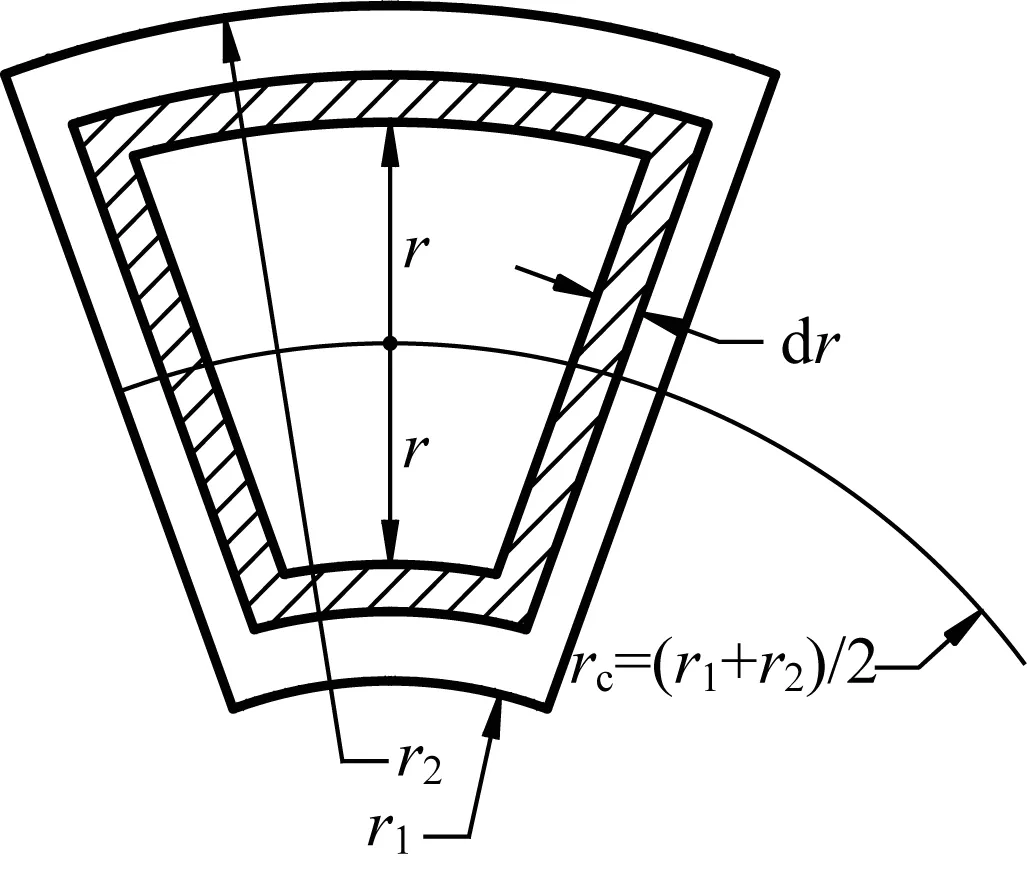
图1 单个磁轭在制动盘上的投影区域Fig.1 Projection area of a single yoke on brake disc

大扇环的总面积Sp为

随着制动盘的转动，该扇形区域和电磁铁的相对位置会发生周期性变化，穿过该扇形区域的磁通量值也将周期性地在正、负峰值之间变化。将该磁通量变化假设为正弦变化，则穿过该扇形区域的磁通量φr可表示为

式中：B为制动盘表面的磁感应强度值，T；ωn为制动盘的电角速度，rad·s-1。

扇形环的感应电动势εr为

扇形环的电阻Rr为

式中：ρ为制动盘材料电阻率，，为涡流的集肤深度，mm；μ0=4π×10-7H·m-1，为真空磁导率；μr为制动盘材料相对磁导率。

根据欧姆定律，从而有扇形环上的电流值即涡流值ir为

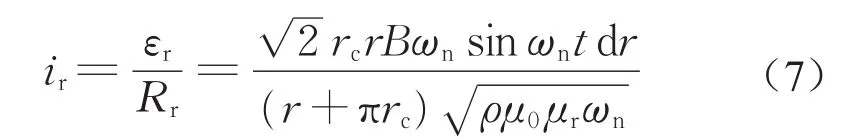
1.3 磁场分析

已知磁路欧姆定律为

式中：εm为磁动势；∑Rmi为磁路中的总磁阻；φi为磁路中穿过各磁阻的磁通量。

由于穿过同一磁路的磁通量处处相同，故可令

本文设计的电磁旋转涡流制动器磁路分析如图2所示。图2a表明，由于电磁铁对称布置于制动盘两侧，且两两相对的电磁铁极性相同，故两侧的磁路相同，因此可得到图2b所示的单侧磁路。图2b中，Rm1为电磁铁支撑架磁阻，Rm2为电磁铁铁芯磁阻，Rm3为磁轭磁阻，Rm4为气隙磁阻，Rm5为制动盘磁阻。

图2 制动器磁路分析Fig.2 Brake magnetic circuit analysis

由于电磁铁支撑架、铁芯、磁轭及制动盘所用材料的相对磁导率均较大，而空气的相对磁导率约为1，而磁阻和材料的磁导率成反比，因此只考虑气隙磁阻，忽略其余的磁阻。从而，图2b可进一步简化为图2c所示的单侧简化磁路。

根据图2c可列出如下磁路方程：

式中：ε0=NI，为电磁铁产生的磁动势；εe=keIe，为制动盘上涡流产生的磁动势；ke为涡流磁通量折算系数；Ie为制动盘上涡流有效值。

由式（7）积分可得整个扇形区域的涡流瞬时值i为

故整个扇形区域的涡流有效值Ie为

从而可获得制动盘上涡流产生的磁动势εe为

气隙磁阻Rm4为度为

式中：δ为气隙大小，m；μr4为空气相对磁导率，μr4≈1。

联立方程（9）、（10）、（13）、（14）可得磁感应强

1.4 功率分析

整个扇形区域的涡流功率瞬时值p为

考虑到每个扇形区域在圆周方向覆盖的角度为40°，且电磁铁在制动盘两侧对称布置，故整个制动盘的涡流功率有效值为

式中：Pe为整个扇形区域的涡流功率有效值；T为制动盘电角速度对应的周期。

1.5 力矩分析

根据能量守恒定律，制动功率等于涡流热功率，即

式中：Pb为制动功率，W；M为制动力矩，N·m；ω=ωn/Np；Np为制动盘单侧磁极对数；ω为制动盘旋转机械角速度，rad·s-1。从而得到涡流制动盘上产生的制动力矩为

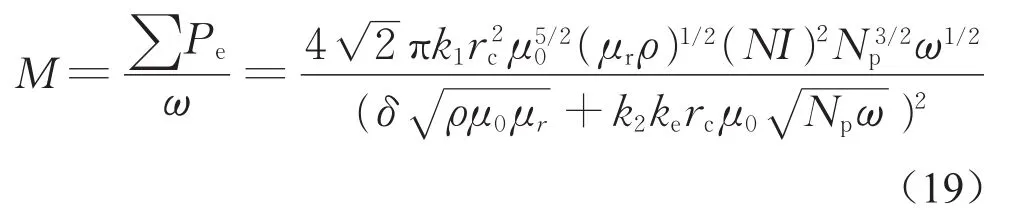
式中：k1、k2均为只和扇形区域尺寸相关的系数，且满足

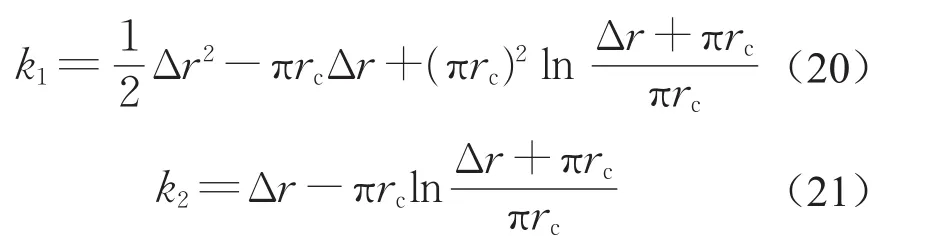
结合制动盘旋转角速度ω、制动盘转速n及列车运行速度v之间的关系可得

式中：v的单位为km·h－1；Dw=845 mm，为车轮直径；n为制动盘转速，r·m－1。

可得制动力矩M和车速v之间的关系为

2 制动力矩控制系统模型

根据前文的制动力矩计算知，制动力矩和制动器的励磁电流密切相关，当励磁电流一定时，列车速度的变化也会影响制动力矩的大小。为了使制动器在不同车速下输出恒定的制动力矩，需要为其设计合适的控制系统。

制动力矩控制系统总体方案如图3所示。系统的基本工作原理为：①从制动器本体模块获取制动器输出的实际制动力矩值，并将其和给定的期望力矩进行实时比较；在制动力矩控制器的作用下，得到励磁电流变化量的参考值。②励磁电流滞环控制器根据输入的变化量参考值输出直流斩波电路的控制信号。③直流斩波电路在斩波信号的控制下，输出相应的电压值。④受控的端电压施加到制动器本体模块的励磁线圈两端，结合列车制动模块反馈的当前列车速度，制动器本体模块将输出受控的制动力矩。

图3 制动力矩控制系统总体方案Fig.3 Overall scheme of torque control system

2.1 制动器本体

制动器本体模块模拟了制动器在不同励磁电流下的制动特性，可根据当前列车速度和线圈电流值输出对应的制动力矩。建模时，选择有限元分析结果作为数据源，将其内置于制动器本体模块中。列车速度、励磁电流以及制动力矩三者之间的关系如图4所示。从该三维曲面的角度来看，恒制动力矩控制实际上是构造一个和该曲面相交的等高面，二者的交点信息包括列车速度和励磁电流大小。列车速度随着制动的进行被动地发生变化，而励磁电流的大小则可主动调节。当确定了当前列车速度后，控制励磁电流大小即可将制动器输出制动力矩控制在等高面附近。在制动器本体模块中，首先将所示制动特性曲面转化为二维数组，然后根据励磁电流和车速通过索引查找数据的方式在数组中定位，得到对应的制动力矩。

图4 制动特性三维曲面Fig.4 Three-dimensional surface of brake torque characteristics

2.2 列车制动模块

在此模块中，考虑了列车运行阻力对列车制动加速度的影响。列车制动时纵向动力学方程为

式中：Fb为制动器提供的制动力；Ff为列车运行阻力，当列车在平直道上施加紧急制动时，附加阻力可视为0，故本文只考虑基本阻力，暂不考虑附加阻力的影响；m0为列车轴重；v为列车运行速度。Fb和Ff分别满足如下公式：

式（26）、（27）中：M为制动器提供的制动力矩；Dw为车轮直径；g为重力加速度，取值9.8 m·s-2；w0为列车单位基本阻力，N·kN-1。在实际运用中，一般认为w0为列车运行速度的二次函数［6］，即

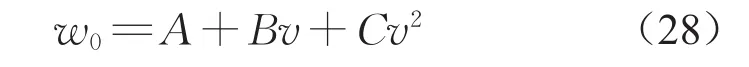
式中：A、B、C为同车型相关的常数。对于时速160 km·h－1单层客车，三者取值分别为1.61、0.004 0、0.000 187［6］，本文将以此参数组合为例进行仿真。联立式（25）～（28），即可获得如下列车制动时纵向动力学方程的完整表达式：

2.3 制动力矩控制器

为了比较各控制方法的优劣，本文设计了PID（比例-积分-微分）控制、模糊控制及模糊自适应PI控制3种控制器。不同控制器采用的控制算法不同，但总体控制思路相同。控制器的输入端包括期望制动力矩和实际制动力矩，输出端为参考电流变化。

2.4 电流滞环控制器

电流滞环控制器的作用为控制励磁电流变化，输出直流斩波电路的开关控制信号。由制动力矩控制器输入的参考电流变化经过一个滞回比较器，当所得结果大于0时，输出“正”的开关信号，斩波电路可控开关闭合；反之，输出“负”的开关信号，可控开关断开。滞环控制器可有效提高系统抗干扰性能。经参数调试，滞回比较器的上、下临界点分别为0.1 A和-0.1 A。

2.5 直流斩波电路

直流斩波电路向制动器电磁铁线圈提供大小合适的电源，其输入为开关控制信号，输出为线圈励磁电流。采用的开关控制信号调节方式为调频调宽。系统随时根据电流滞环控制器输出的信号，调节可控开关的状态。

将上述各子模块按一定顺序连接，并添加期望制动力矩，即可得到完整控制系统，如图5所示。

图5 控制系统模型Fig.5 Control system model

3 控制算法说明

如前所述，本文设计的制动力矩控制算法包括PID控制、模糊控制、模糊自适应PI控制。

3.1 PID控制

PID控制是经典控制理论中一种成熟的控制算法。P、I、D分别代表针对系统偏差进行比例、积分、微分变换。比例环节可减小系统的稳态误差，并加速系统的响应；积分环节的作用是消除系统稳态误差；微分环节可预测系统偏差。通过PID参数整定，可得到令人满意的控制效果［7］。在本文中，参数整定后所得 PID 参数Kp、Kd、Ki分别为 1.5、0.25、0.001 25。

3.2 模糊控制

对于非线性系统，经典控制理论往往存在较为明显的局限性，而模糊控制可根据对变量的模糊化感知，并基于事先设定的规则，实现对系统的精确控制［8］。在本文模糊控制算法中，系统输入变量为制动力矩误差e及制动力矩误差变化率ce，输出变量为参考电流变化I。各变量采用相同的模糊状态词集｛NB，NS，PS，PB｝，其中各模糊状态分别对应｛负大，负小，正小，正大｝，表示变量值的符号及绝对值大小。各模糊状态隶属度函数统一设置为三角形函数，如图6所示。根据制动力矩误差和参考电流变化之间的定性关系，制定模糊规则表，如表1所示。本文所选去模糊化方法为常用的重心法。

图6 模糊状态隶属度函数Fig.6 Membership function of fuzzy state

表1 模糊规则表Tab.1 Fuzzy rules

3.3 模糊自适应PI控制

模糊自适应PI控制基于PID控制和模糊控制，运用模糊数学的基本理论和方法，把规则的条件、操作等用模糊集表示，根据控制系统的实际响应情况，对PI参数进行自动调整。本文以制动力矩误差e及误差变化率ce作为输入，不断检测e和ce的大小，根据模糊规则进行PI参数的自整定，得到PI的2个参数修订值ΔKp和ΔKi。根据制动力矩误差和PI参数之间的定性关系，建立PI参数的模糊规则表，见表2和表3。

表2 ΔKp的自适应模糊规则表Tab.2 Adaptive fuzzy rules of ΔKp

表3 ΔKi的自适应模糊规则表Tab.3 Adaptive fuzzy rules of ΔKi

输入变量制动力矩误差e及误差变化率ce，采用与3.2节中相同的模糊状态子集，输出变量ΔKp、ΔKi的模糊状态子集为｛B，M，S｝，其中各模糊状态分别对应｛大，中，小｝，且各模糊状态隶属度函数统一设置为三角形函数，然后计算出隶属度值，根据隶属度赋值表和各参数的变化规律，应用模糊合成推理出PI参数的模糊规则表，查出修正值，代入下式计算：

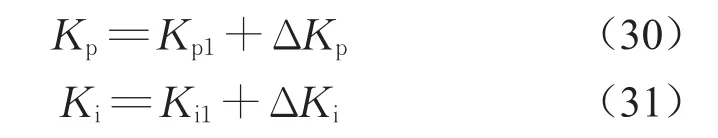
式中：Kp1和Ki1为前一次整定后的PI参数。

4 仿真结果对比

本文设定了两种仿真工况，系统仿真时间均为100 s，仿真固定步长均为0.000 1 s。工况一，给定期望制动力矩为3 500 N·m的恒定值，列车制动初速度为 160 km·h－1；工况二，给定期望制动力矩为4 500 N·m的恒定值，列车制动初速度为200 km·h－1。

本文主要从两个方面对比仿真结果：①开环控制和闭环控制的对比；②不同闭环控制算法之间的对比。为此，将各控制方式下仿真所得制动力矩随列车速度变化曲线及时间历程曲线汇总于图7和图8中。

由图7和图8中两种工况的对比结果图可以发现，两种工况的制动力矩随列车速度变化曲线及制动力矩时间历程曲线的总体变化趋势是一致的，且输出制动力矩都能稳定地达到输入的目标制动力矩，故下面主要就工况一的仿真情况进行分析。

首先，通过图7对比系统在开环控制和3种控制算法下的响应可以发现，在开环控制下，当线圈电路稳定之后，励磁电流即保持不变，随着制动的进行，制动力矩先增后减，呈现较大的变化，列车制动减速度也因此而发生明显波动；在闭环控制下，当线圈上电之后，励磁电流迅速增大，且系统根据当前制动力矩反馈，实时地对励磁电流的大小进行调整。从列车开始制动到列车速度减至略低于20 km·h－1之间，实际制动力矩值被控制在期望制动力矩值附近；当列车速度继续下降时，由于线圈电流无法继续增大，制动器在低速下可输出的最大制动力矩受到限制，制动力矩这时才开始随着速度的下降而减小。在3种控制算法下，制动力矩开始减小时对应的列车速度分别为 16.05 km·h－1、16.25 km·h－1、16.06 km·h－1。可见，对于控制制动力矩而言，3种控制器都发挥了显著的作用，在较大的速度范围内都可有效控制制动力矩基本保持恒定.

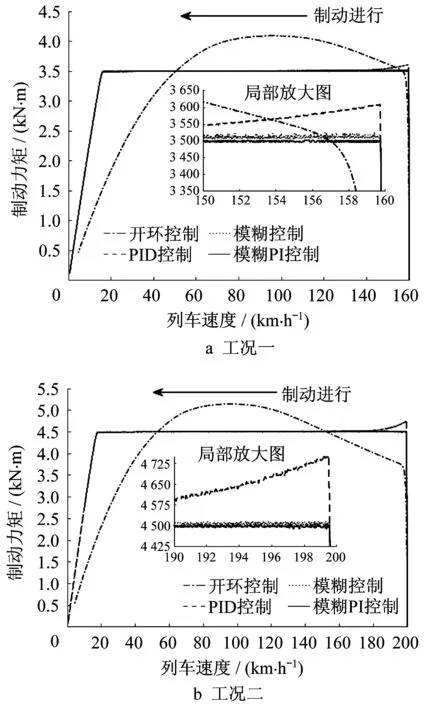
图7 各控制方式下制动力矩随列车速度变化曲线Fig.7 Brake torque versus train speed in different control algorithms

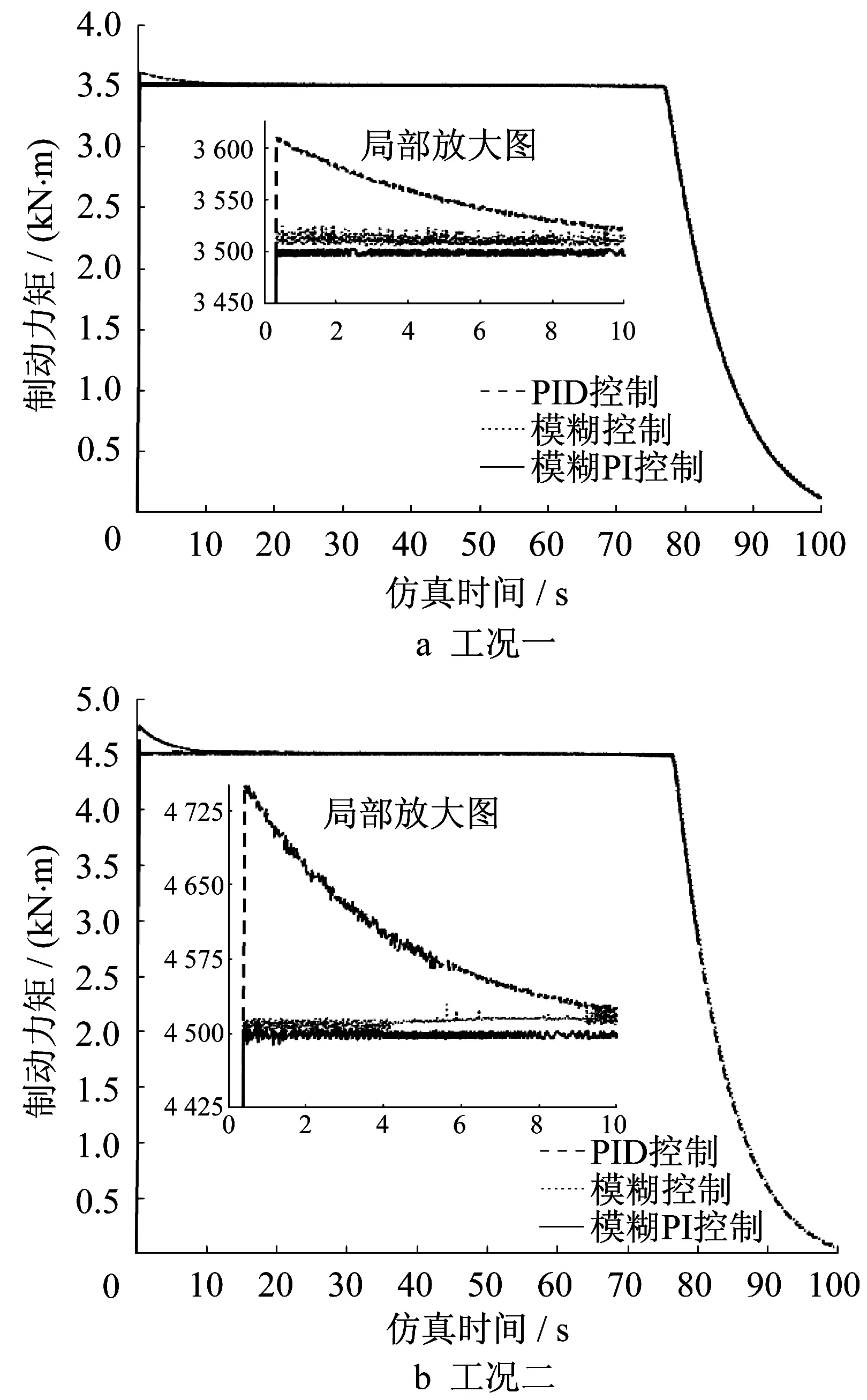
图8 各控制方式下制动力矩时间历程曲线Fig.8 Brake torque in different control algorithms

其次，通过图8对比系统在3种控制算法下的时间响应可以直观地发现，系统在开环控制下存在明显的超调，而系统在模糊控制和模糊PI控制下都不存在较大的超调。为了定量说明系统在3种控制算法下的响应情况，将3种算法的瞬态和稳态性能指标列于表4中。

表4 各控制算法下系统瞬态和稳态性能指标Tab.4 System performances of transient and steady state

由表4可知，就瞬态性能指标而言，系统在PID控制下的最大超调量为111.7 N·m，远大于系统分别在模糊控制和模糊自适应PI控制下所得的26.2 N·m和4.6 N·m的超调量。此外，系统在PID控制下的调整时间最长，为3.210 s，而系统在模糊控制和模糊自适应PI控制下的调整时间都仅为0.318 s。综上可见，系统在模糊自适应PI控制下所得瞬态性能最佳，模糊控制次之，而PID控制表现不如其余二者。就稳态性能指标而言，系统在3种算法下的表现略有差异，系统在模糊自适应PI控制下所得稳态平均值最接近给定的期望制动力矩3 500 N·m，在模糊控制下所得结果次之，在PID控制下所得结果偏离期望值程度最大。此外，根据稳态方差可判断，系统在模糊自适应PI控制下稳态输出最稳定，在模糊控制下的稳态输出次之，在PID控制下的稳态响应则呈现相对较大波动。综上可见，就系统稳态性能而言，模糊自适应PI控制依然表现最佳，模糊控制次之，PID控制相对最差。

综合考虑系统瞬态性能指标和稳态性能指标，模糊自适应PI控制相对于其余两种控制算法都呈现了明显的优势，而模糊控制相对PID控制也表现更佳。仿真结果充分体现了模糊自适应PI控制和模糊控制等智能控制算法在非线性系统上的应用优势。需要补充说明的是，良好的控制效果需要付出一定的代价。由于本文中模糊自适应PI属于二维模糊控制器，输出变量较本文中模糊控制器多，对应的模糊规则数量也较多，计算量较大，仿真时花费的时间也显著变长，实际应用时对控制器硬件的要求也将提高。因此，在实际开发控制器时，若选用的硬件性能较高，则推荐使用模糊自适应PI控制作为控制算法，以提高控制器的响应速度和稳态精度；若选用的硬件性能不足以实现模糊自适应PI控制算法，则推荐使用模糊控制作为控制算法，以使得控制器的响应速度和稳态精度在可接受的范围内。