同时同频全双工数字快速自干扰抵消算法

芮正雄, 赵彦龙, 陈 旭, 胡 阳

(1.上海无线电设备研究所,上海201109;2.空军装备部驻上海地区第一军事代表室,上海201109)

0 引言

随着第五代移动通信(简称5G)在国际范围内商用进程的迅速推进,具有更高通信速率和吞吐量的同时同频全双工通信成为研究热点[1]。移动通信系统常用的双工方式有三种:时分双工(TDD)、频分双工(FDD)和同时同频全双工(CCFD)。同时同频全双工(以下简称全双工)突破了现有的频分双工和时分双工模式,保证无线通信设备的发射机和接收机在占用相同频率资源时可同时工作,是5G的关键技术之一。

全双工系统收发链路之间的信号隔离有限,通常近端发射信号泄漏到接收机的信号功率,比接收机接收到的远端发射机发射的信号功率大很多,泄漏信号会淹没接收到的远端发送信号,甚至使接收链路饱和阻塞,这种现象称为自干扰[2]。目前研究的自干扰抵消方法主要包括天线自干扰抵消、射频自干扰抵消和数字自干扰抵消。天线自干扰抵消通过选择恰当的天线形式与天线排布方式,或通过增加辅助天线进行天线调零,减少到达接收天线的自干扰信号;射频自干扰抵消通过重建射频自干扰信号,并将其从射频接收通道中减去,实现对自干扰的抵消。然而,射频自干扰信号并不能完全被抵消掉,因此在数字域进行自干扰抵消是不可缺少的。

数字域自干扰抵消的主要方法是:首先对自干扰信道进行精确估计;然后利用反馈信号与自干扰信道估计值来重建自干扰信号;最后从接收信号中减去重建的自干扰信号,实现自干扰信号的抵消。本文研究了基于快速横向递归最小二乘(fast transversal recursive least squares,FTRLS)的数字自干扰抵消算法,并在自干扰抵消能力、收敛性能、误码率等方面与递归最小二乘(recursive least squares,RLS)算法、最小均方(least mean squares,LMS)算法等进行比较。

1 全双工数字自干扰抵消系统

1.1 全双工系统

全双工系统包括近端设备与远端设备,如图1所示。

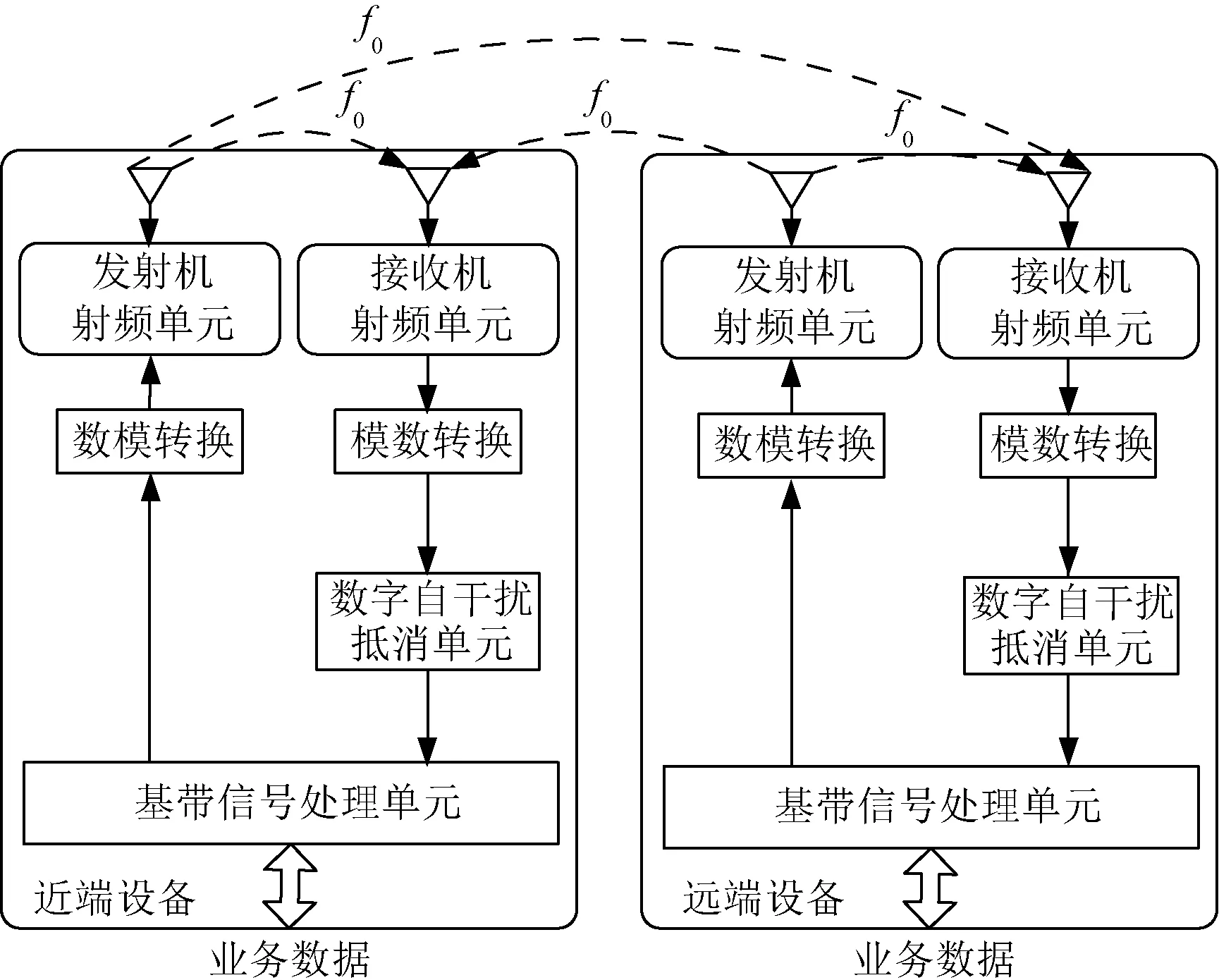
图1 全双工系统原理框图

信号的发送与接收在频率f0同时进行。近端接收机能同时接收到近端与远端发射机发射的信号。其中,近端接收机接收的远端发射机发射的信号为期望信号,接收的近端发射机发射的信号为自干扰信号。该全双工系统的典型信号处理流程为:近端(远端)业务数据经过基带信号处理单元完成组帧和上变频后,通过数模转换器(DAC)进行数模转换,再经发射机射频单元变频、放大、滤波后通过天线发射出去。接收信号经射频自干扰抵消后包含期望信号、接收噪声与残余自干扰信号。由于残余自干扰信号的存在,接收信号的信噪比无法满足解调需要。因此,需要在数字中频或数字基带采用数字自干扰抵消算法完成残余自干扰消除,保证经过数字干扰抵消后的接收信号通过基带处理能正确译码[3]。

1.2 数字自干扰抵消系统

数字自干扰抵消系统主要由自干扰信道估计模块和自适应滤波器模块组成,系统原理框图如图2所示。其中,z(n)是模数转换后的接收信号,x(n)是近端设备发射的基带信号,(n)是重建的自干扰信号。

图2 数字自干扰抵消系统原理框图

为了使自适应滤波器输出一个初始的自干扰估计样本,必须通过自干扰信道估计来为滤波器提供一个初始权值。无线通信信道最明显的特征是多径效应和时变特性,即无线信道是时变多径衰落信道。不失一般性,信道模型可表示为离散时间的有限冲激响应(FIR)滤波器模型,表达式为

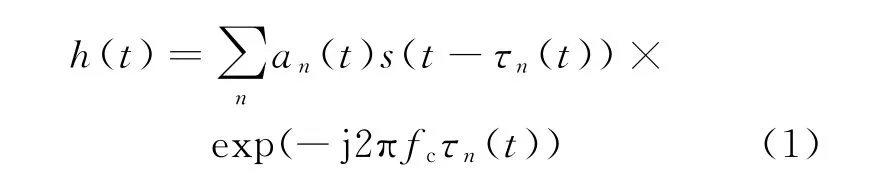
式中:n为多径数目;a n(t)为第n条路径的衰减系数;τn(t)为第n条路径的传播时延;s(t)为输入有用信号;fc为载波频率。

这样,只要求出h(t)的各个参数,就可以获得自干扰信道特性。通常采用基于训练序列的估计方法,利用发射端和接收端已知的序列,结合一定的估计准则来完成信道估计[4]。

考虑到无线通信信道的时变特性,将所求出的信道冲激响应的加权系数作为自适应滤波器的初始系数,再采用自适应算法对滤波器系数进行调整,当输入为本机的基带信号时,滤波器的输出能最大程度地接近自干扰信号。这样,即可利用自适应滤波器实现自干扰的自适应抵消。

2 基于FTRLS算法的自适应干扰抵消

2.1 自适应抵消算法

将所求出的信道冲激响应的加权系数作为自适应滤波器的初始系数,发射端基带信号作为滤波器的输入信号。这样,滤波器先输出一个初始的自干扰重建信号,然后用模数转换量化后的接收信号减去这个重建信号,得到的信号包含自干扰抵消后的误差信号以及有用信号,并反馈到滤波器。如果自干扰信号发生变化,那么误差信号也会随之改变。此时自适应滤波器依据相应的算法自适应调节其加权系数,使输出的估计信号逐渐逼近自干扰信号,从而使得误差信号趋于零。因此,自干扰抵消处理后的接收信号会更加接近于有用信号。

对于时变多径衰落信道的估计,其主要目标是估计出N阶自干扰重建滤波器的抽头系数向量w N(k)=[w1(k),w2(k),…,w N(k)]T,滤波器结构如图3所示。

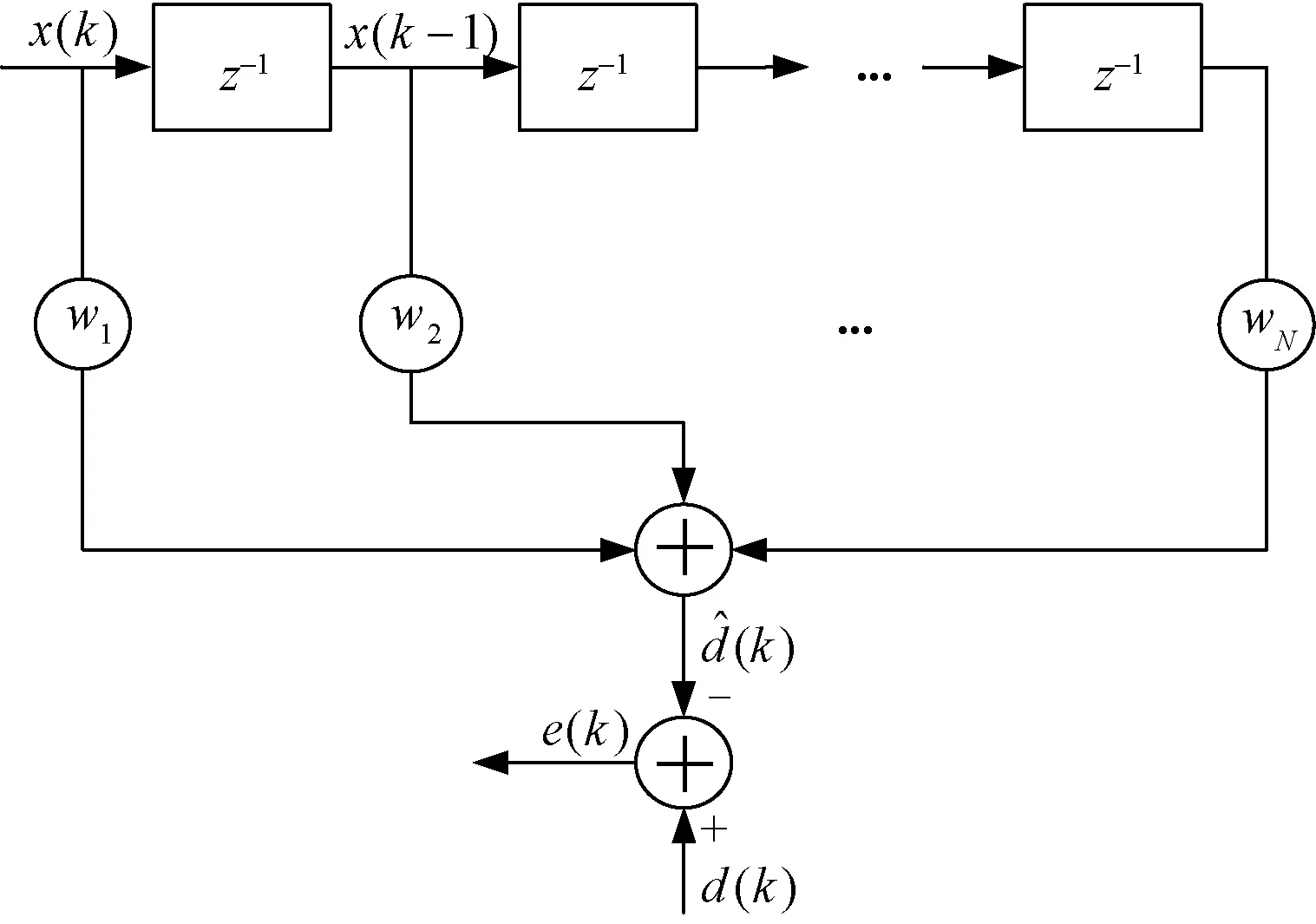
图3 N阶自干扰重建滤波器系统模型

输入信号向量

代表数字域的自干扰参考信号。参考信号经过重建滤波器后,其输出信号为数字自干扰重建信号,表达式为

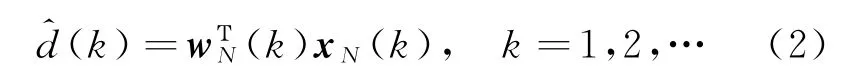
设d(k)为模数转换后的接收信号,则相应的估计误差为

2.2 FTRLS算法原理

时变多径衰落信道估计方法包括自适应方法和非自适应方法。自适应方法是基于RLS、LMS等准则衍生出的能实时跟踪自干扰信道变化的方法。常规RLS算法中,单次迭代计算量会随着阶数N的增大而增大。为了将计算量由O(N2)降低至O(N),研究人员提出了FTRLS算法[5]。FTRLS算法主要利用了前向预测器、后向预测器和联合过程估计器具有相同的转换因子和增益向量的特点,实现RLS算法的快速收敛。

(1)前向预测

对一个N阶前向预测器的抽头系数进行最小二乘意义下的优化。设k时刻的滤波器抽头系数向量为

a N(k)=[a1(k),a2(k),…,a N(k)]Τ,自干扰参考信号输入向量为

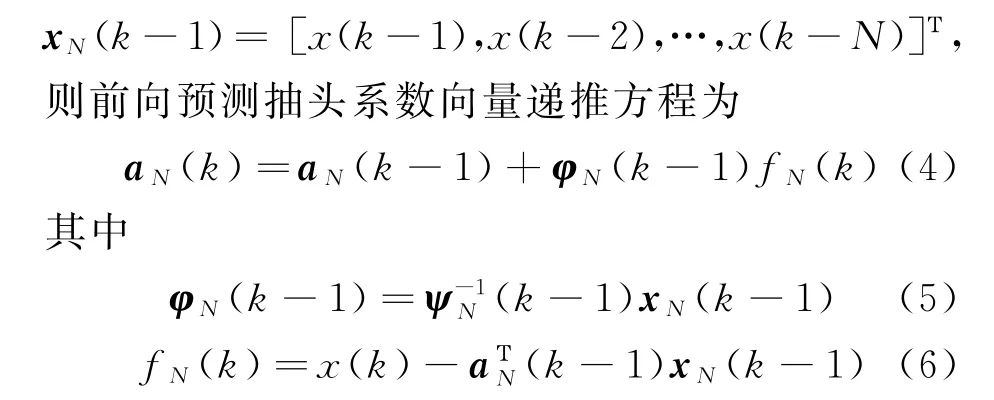
式中:φN(k-1)和fN(k)分别为前向预测器的增益向量和先验估计误差;为抽头输入向量的自相关矩阵逆运算。

先验是指利用k-1时刻的抽头系数向量估计k时刻的输出,而后验是指利用k时刻的抽头系数向量估计k时刻的输出。

(2)后向预测

设在N阶后向预测器中,预测器抽头系数向量与自干扰参考信号输入向量分别为gN(k)和xN(k),后向预测抽头系数向量递推方程为

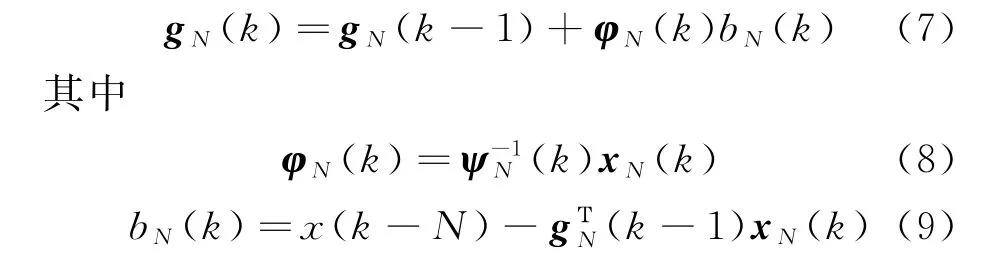
式中:φN(k)和bN(k)分别为后向预测器的增益向量和先验估计误差。

对于一个给定时刻k,N阶前向预测器的增益向量等于k-1时刻后向预测器的增益向量。

(3)联合过程估计

设N阶抽头联合估计器的抽头系数向量为wN(k),联合估计器的后验估计误差(k)可以表示为

前向预测器的先验估计误差fN(k)与后验估计误差的关系可表示为

同理,后向预测器的先验估计误差bN(k)与后验估计误差的关系可表示为

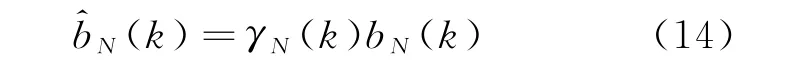
定义归一化的联合估计器增益向量

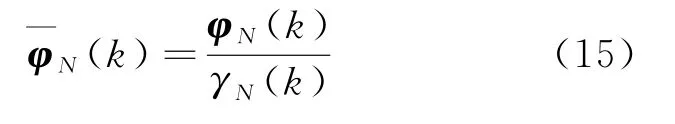
因此,N阶抽头联合过程估计器的转换因子亦为式(12)给出的γN(k)。

则自适应滤波器的抽头系数向量递推方程为

在第k次迭代中,抽头系数的改变量取决于归一化的增益向量与后验估计误差的乘积。

RLS算法的计算复杂度与滤波器长度N的平方成正比,而FTRLS算法计算复杂度仅随滤波器长度的增加线性增加[6]。

3 仿真验证

用干信比表示干扰抵消前干扰信号功率与有用信号功率的比值,分别采用FTRLS、RLS和LMS三种自适应滤波算法进行自干扰信道估计仿真,对比不同算法的自干扰抵消能力、误码率和收敛时间参数指标。仿真参数设置为:有用信号带宽10 MHz,干扰信号带宽20 MHz,载波频率2.4 GHz,调制方式二进制相移键控(BPSK),信噪比0 d B,干信比(30～75)d B。

(1)干扰抵消能力

在滤波器阶数为8的情况下,各算法干扰抵消能力与干信比关系的仿真结果如图4所示。在干信比相同的情况下,三种信道估计算法的自干扰抵消能力由高到低依次为FTRLS、RLS、LMS;在滤波器阶数一定的情况下,随着干信比的增大,自干扰信号的抵消能力越来越大,这是由于自干扰信号功率增强,更多的自干扰信号被抵消掉。

图4 干扰抵消能力与干信比关系

在干信比为30 d B的情况下,各算法干扰抵消能力与滤波器阶数关系的仿真结果如图5所示。在干信比相同的情况下,滤波器的阶数增加,各算法的干扰抵消能力也随之增加;在滤波器阶数相同的情况下,三种信道估计算法的自干扰信道估计能力由高到低依次为FTRLS、RLS、LMS。

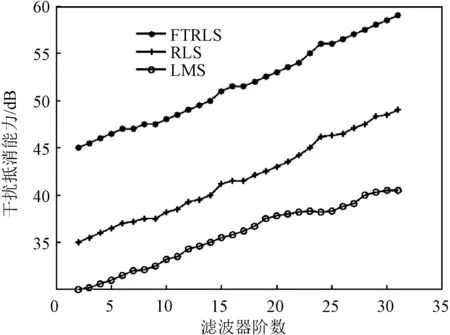
图5 干扰抵消能力与滤波器阶数关系

(2)误码率

在滤波器阶数为20的情况下,各算法误码率与干信比关系的仿真结果如图6所示。随着干信比的增加,三种算法的误码率呈上升趋势;在干信比相同的情况下,三种算法的误码率由大到小依次为LMS、RLS、FTRLS。

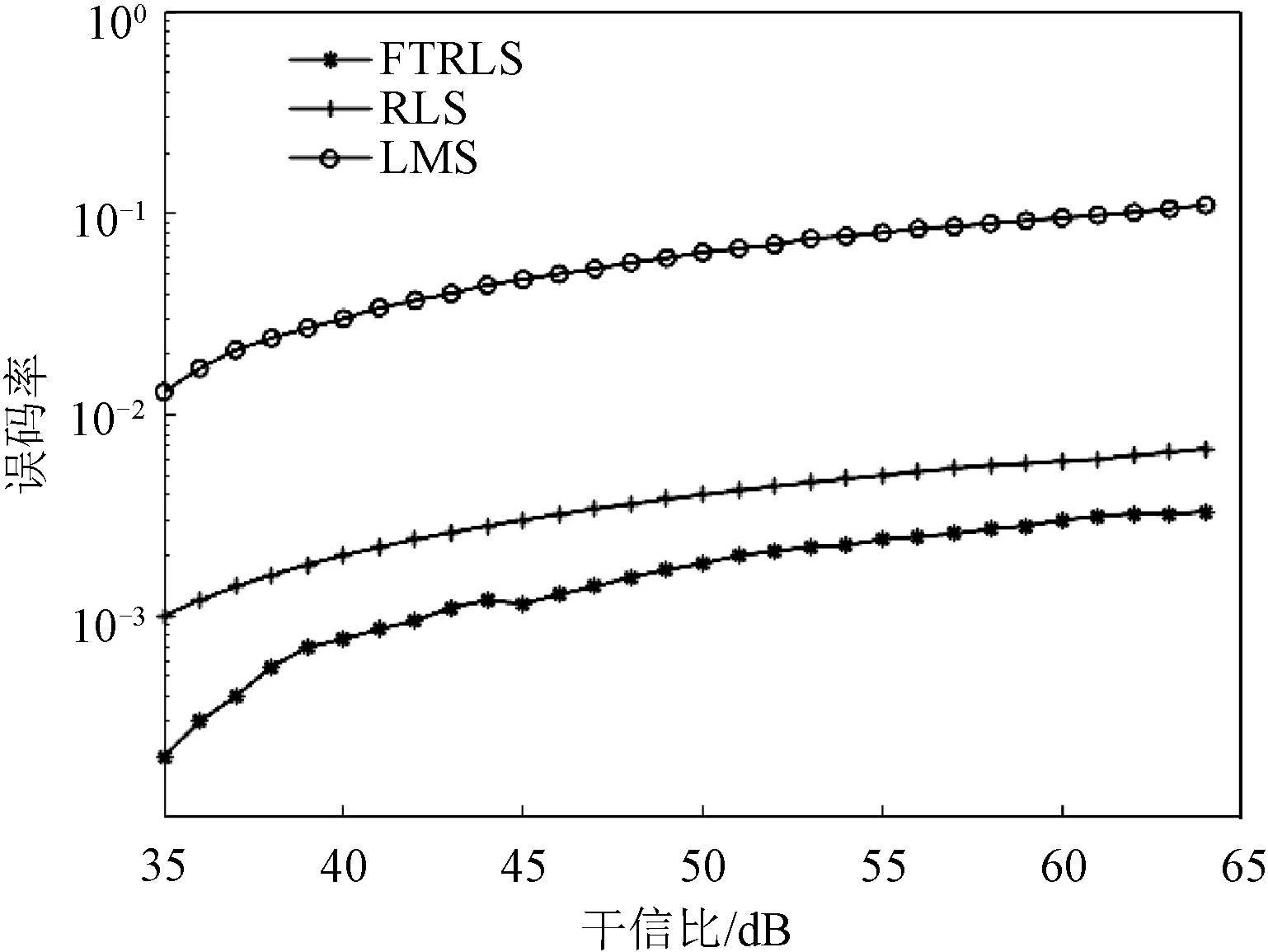
图6 干信比与误码率关系

(3)收敛速度

在干信比为30 dB,滤波器阶数为8的情况下,各算法收敛速度的仿真结果如图7所示。LMS算法与RLS和FTRLS算法相比,收敛速度有较大差距,且信号起伏较大;FTRLS算法的收敛速度优于RLS算法,且算法收敛后的自干扰抵消能力与RLS算法基本一致。

4 结论

针对同时同频全双工通信系统数字域的自干扰抵消问题,以FTRLS为自干扰信道估计算法,分析其自干扰抵消能力、误码率和收敛速度,并与RLS和LMS算法进行对比。仿真结果表明:在同一条件下,FTRLS自干扰信道估计的自干扰抵消能力和误码率优于RLS和LMS算法,且收敛速度最快、收敛后的性能最好。