基于改进哈希算法的图像相似度计算

胡新荣，欧阳祥,刘军平

(1.武汉纺织大学 数学与计算机学院，湖北 武汉 430200；2.湖北省服装信息化工程技术研究中心，湖北 武汉 430200)

随着网络时代的快速发展，多媒体技术广泛地应用在多种场景，导致互联网上的图像呈爆炸式增长，数量达到了上千亿级。图像是人们生活中的信息载体，如何在庞大的图像库中快速地、精确地完成相似图片的检索成为了一个热门的课题，而针对相似图片的检索重要的步骤就是图像的相似度计算。

图像相似度的快速计算可以采用哈希算法，就是把图像信号压缩到一个固定长度的哈希值，对于相同内容的图像，其哈希值应该也是相同，即图像哈希具有较好的唯一性[1]。一般而言，图像哈希序列的生成主要分为图像预处理、特征提取与哈希序列的生成这三个过程，而特征提取尤其关键，其鲁棒性的高低对整个哈希算法有很大的影响[2]。从Schneider[3]提出第一个灰度直方图构成哈希的图像认证方法开始，哈希算法被应用于图像处理的各个领域；在图像检索中，一种新兴的哈希算法是基于深度网络的哈希方法，例如文献[4-7]提出了几种基于深度网络的哈希方法，通过深度神经网络学习图像的哈希码。但是基于深度网络的哈希方法需要大量数据集去训练模型，整个的检索速度慢。在非监督学习的哈希方法中，Kozat[8]提出一种基于图像奇异值分解(singular value decomposition,SVD)的哈希算法，将随机组成的特征图像进行SVD分解后得到特征矢量来构成哈希序列，实验表明，这种算法虽然几何变换具有一定的稳健性，但是有较高的误分类概率；Lin[9]提出了一种兼容JPEG压缩的认证方法，其利用在分块DCT变换后，任意块的相同位置的系数在JPEG压缩前后保持不变的大小关系来构成哈希，实验结果证实了方法对JPEG图片的稳健性，但在分块离散余弦变换时存在方块效应，导致算法鲁棒性不高；Qin[10]等提出基于显著结构特征的图像哈希算法，利用离散余弦变换（discrete cosine transform,DCT）机制对图像进行分解，联合主成分分析（principal components analysis,PCA）来生成对应哈希序列，但是该算法仅利用了边缘特征，整体的鲁棒性也不高。

针对图像处理中的噪声影响和DCT变换中存在的方块效应，本文提出一种基于SVD-DWT的哈希算法来计算图像的相似度。

1 理论基础

1.1 奇异值分解

矩阵A为m×n阶矩阵，则可以将矩阵A分解使得：

（1）式中 A 的奇异值为σ1，σ2,…,σr，设Δr=diag（σ1，σ2,…,σr），U 为m×m阶的正交阵，VT为一个n×n阶的正交阵，其中，

(1)式中，矩阵U的第i列为与A相对应的奇异值的左奇异向量ui，矩阵V的第i列为与A相对应奇异值的右奇异向量，Σ为奇异值对角矩阵。则对于任意的图像A，我们可以将A分解为：

公式（3）表明一幅图像A可以由r幅子图像组成，每一幅子图像对应一个奇异值，而图像的大部分信息都集中在前面较大的奇异值中，较小的奇异值对于整幅图像的贡献较小[11]，因此可以取前面较大的奇异值对应的子图像来代替整幅图像。

假设纯净的图像信号为Y[n]，噪声信号为Z[n]，则包含噪声的图像信号可以表示为X[n]=Y[n]+Z[n](n=0，1，2，…，K-1)，K为输入数据的长度。其中M≥N，且M+N=K+1。首先我们要建立Hankel矩阵 P∈RM×N。

矩阵R可以表示R=S+D，其中S为不受噪声干扰的m×n阶的Hankel矩证，D为噪声信号构成m×n阶的Hankel矩阵。然后对矩阵R进行奇异值分解，确定奇异值对角阵Σ的有效秩，即前p个最大的奇异值，然后可以得到下式：

Rp按照下式构造不受噪声干扰的信号分量构成的Hankel矩阵Sˆ。

1.2 离散小波变换

设ψ（t） ∈L2（R），其傅里叶变换为（ω），若ψ（t）满足允许条件：

则ψ（t）称为小波基函数，将其按照伸缩因子a和平移因子b两个参数进行平移、伸缩后得到小波序列

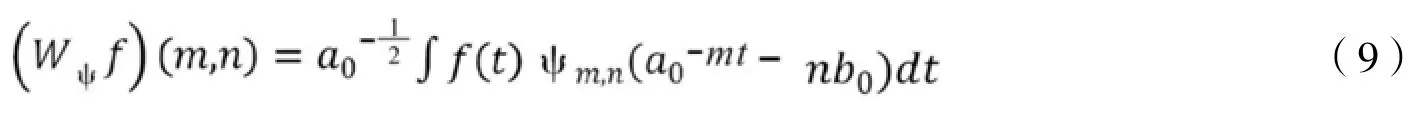
(9)式中m为频率范围指数，n为时间步长变化指数。

图1为离散小波分解过程，图像每经过稀疏变换一次，经过不同低通滤波器h和高通滤波器g的分解，通过降采样滤波器Q得到四个分量LL、LH、HL、HH，其中LL表示近似系数的低频分量，LH、HL、HH表示三个高频分量，分别为水平、垂直、对角线方向的分量，而本文中只需要得到低频分量LL。

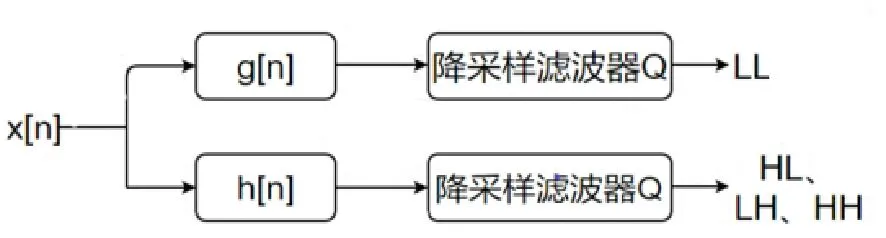
图1 小波分解示意图

图2 DCT变换示意图

2 改进的哈希算法

本文中提出的SVD-DWT哈希算法是一种基于频谱的无监督学习的哈希方法，无需大量的带标签的数据集，通过生成一段紧凑的二进制码，比较其汉明距离从而得到图片的相似度。

2.1 方块效应

如图2所示，在DCT处理图像时，为保证图像处理的速度与质量，通常将图像分割成不重叠的8×8大小或者16×16大小方块，然后对每一个独立的小方块进行单独编码，然后复原，这使得每个方块之间信号的连续性被人为分割，从而导致方块效应，而DWT是将整张图像进行分解得到低频部分的图像，再对低频图像进行操作，融合了整张图片的信息，包括一些重要的边缘信息，从而消除方块效应。

2.2 基于SVD-DWT的图像哈希算法

图3表示基于SVD-DWT的图像哈希算法的流程图，具体步骤如下：

步骤1：对输入图像进行判断，如果为灰度图像直接进行步骤2，如果为彩色图像则进行灰度化处理；

步骤2：利用灰度图片构建Hankel矩阵，利用公式（1）对矩阵进行奇异值分解，利用（3）式得到r个子图像Ai（其中i=1，2，3，…，r），仿真过程中发现奇异值个数取值太小，图片还原的清晰度差，个数取值太大会导致去噪效果不好，取60-80个奇异值去噪还原的效果最佳[13]，因此文中选取r=60，分解后得到降噪后的图像信号

步骤3：利用公式（9）对降噪后的图片进行第一级离散小波变换分解成四个子图像，本文中选择的小波基函数ψ（t）为Biorthogonal小波函数，它是一个双正交小波函数，具备正则性，分解后的图像保留低频分量LL；

步骤4：将得到的低频子图像LL缩小为16×16大小，计算缩小后图像的像素平均值，遍历所有像素点的像素值，大于平均值的记为1，其他的记为0，得到256位二进制哈希码；

步骤5：计算两幅图像哈希码之间的汉明距离，由汉明距离得到两幅图片的相似度。汉明距离是一个概念，它是描述之间的距离D(x，y)，如下式：

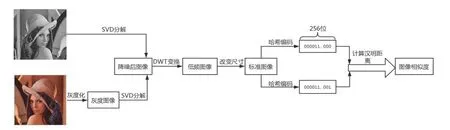
图3 基于SVD-DWT图像哈希算法流程图

3 实验

3.1 评价标准

3.1.1 PSNR

假设存在两个m×n单色图像I和K，则有：

峰值信噪比定义为：

其中MAXI为图像像素值的最大值，如果图像用8位表示，值就为255。通常来说，峰值信噪比越大，去噪后图片失真越少，质量就越好。

3.1.2 图片的相似性

定义两幅图片的相似度可以用公式（13）：

其中D(x，y)表示两幅图像的汉明距离，sim(x，y)∈[0，1]，表示m×n阶图片M1与图片M2的相似度。

3.2 实验方案

为了验证文中提出的算法的性能，选取9张经典的灰度图像进行仿真实验，图片包括Baboon、carmeraman和lena等9幅图片。本次实验仿真平台为Windows 10操作系统，CPU为Inter(R)Core(TM)i5-7300HQ处理器，8G内存，仿真环境为Matlab2010a。以lena为例，图4是经过翻转、模糊、旋转、缩小尺寸等操作后的图像。

图4 图像变换示例

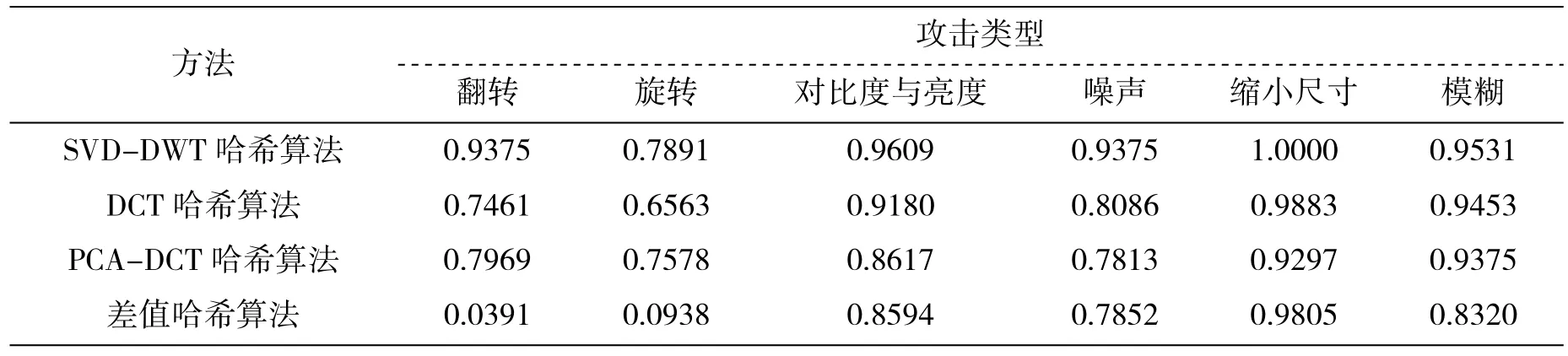
表1 lena相似度计算结果

基于SVD哈希算法对图像区分度太低，因此本文将与DCT哈希算法、PCA-DCT哈希算法和差值哈希三种方法进行比较，在图片经过旋转、翻转、改变亮度与对比度、模糊、改变尺寸和加入噪声的攻击下，通过汉明距离计算与原图像的相似度。其中翻转是左右翻转，旋转是将图片向左旋转10度，改变尺寸是将图片缩小至原来图片的四分之一，加入噪声是在图片中随机加入百分之十的椒盐噪声和百分之十的高斯噪声，模糊是对图像进行高斯模糊，表1是lena图像的实验数据。

图5 图像降噪质量

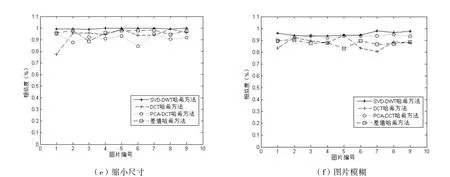
图6 图像相似度计算结果

3.3 实验结果

3.3.1 降噪效果

如图5所示，实验图片经过不同方法降噪后得到的图像的PSNR结果，经过奇异值分解降噪后的图片质量比经过均值滤波、高斯滤波、中值滤波和双边滤波降噪后的图片质量好，所以本文选择SVD分解对图片进行降噪处理。

3.3.2 图像相似度计算

为了测试算法的鲁棒性，本文与DCT哈希算法、PCA-DCT哈希算法和差值哈希算法进行比较，实验结果如图6所示，图6（b）-图6（f）分别对应图像经过翻转、旋转、改变对比度与亮度、加入噪声、缩小尺寸和模糊六种攻击，利用本文的方法计算图片相似度相对于DCT哈希算法分别提高了9.82%，10.24%，19.77%，20.4%，5.72%和7.82%，相对于PCA-DCT哈希算法分别提高了3.9%，3.11%，11.47%，16.23%，8.46%和2.38%，差值哈希算法在图片旋转和翻转的时计算图片平均相似性度分别只有12.1%和12%，说明差值哈希算法在图片旋转和翻转时鲁棒性极差，本文算法在图像改变亮度与对比度、加入噪声、缩小尺寸和模糊的时，相对于差值哈希方法相似度分别提高了11.47%，16.23%，3.48%和7.57%。因此本文提出的算法在图片改变亮度与对比度、图片旋转、图片模糊、缩小尺寸、图片翻转和加入噪声时鲁棒性较高。

4 结束语

本文提出的基于SVD-DWT的哈希算法，利用SVD分解图像，消除了噪声对整体图像相似度计算时的影响，通过DWT变换获取图像的低频部分，低频代表图像的主体部分，将其用于后续的相似度计算，在图像几何变换和亮度改变时的实验结果表明，文中算法鲁棒性要优于传统算法。通过DWT替换DCT变换，解决了变换过程中存在的方块效应，在图像快速检索方面有重要意义。但是由于文中采用的是灰度图像，在彩色图片转变为灰度图像的过程中不免造成信息丢失，因此，下一步的工作是改进算法，需要针对彩色图像的变换进行研究，对算法进行改进。