基于多元回归方法的海洋执法船主尺度分析
2020-06-15李宏伟
李宏伟,管 官
(1.黄海造船有限公司生产设计处,山东荣成 264309;2.大连理工大学船舶工程学院,辽宁大连 116024)
0 引言
随着海洋经济的发展,近海及沿海海域海上交通繁忙,海难事故增多,远海海域与领国间岛礁争端与冲突增多[1]。为维护我国的海洋权益,不仅要壮大我国的海军力量,还要加强对渔业、海洋巡航的管理与监视,提高海洋权益的维护能力[2]。海洋执法船在维护我国领海主权、维持海上公共秩序、保护海洋环境等方面发挥了重要作用。作为海洋执法船的一种,海监船的主要职能是按照相关法律法规,对我国所管辖的海疆海域进行巡航监视,对破坏海上设施设备、违法违规使用海域、扰乱海上公共秩序、侵犯我国海洋权益等违法违规行为进行查处等;另一类重要的海洋执法船—渔政船是用来在渔业专属海域进行渔政工作的船舶,主要可用来巡视监督渔场、检查渔船是否执行与渔业相关的法律法规,防止违规排放污油、废弃物等有毒有害物质,防止渔民滥捕、维护渔场渔业生产秩序等。海监船和渔船对国家的环境保护、渔业生产、海南救助、主权维护等任务起到了积极的作用[3]。
随着执法需求的日益增加以及执法复杂程度的提高,业内迫切需要设计和建造吨位大、用途广、航速高的海洋执法船[4]。近几年来,我国批建了多艘设备更先进、功能更强大的、用途更广泛的海洋执法船[5-6]。本文针对海洋执法船的设计特点,采用多元回归分析方法,对国内外100艘海洋执法船及相近船型的主尺度进行了分析,考虑船舶主尺度与总吨位、排水量等关系的复杂性[7],将多个变量引入总吨位、排水量回归模型以提高模型的拟合精度,为海洋执法船后续总体设计提供参考。
1 多元回归分析
回归分析是一种传统应用性较强的科学方法,它通过一组预测变量(自变量)来预测1个或多个响应变量(因变量)[8]。在大多数实际工程问题中,影响因变量的因素通常不止1个,而是多个,一般称这类问题为多元回归分析问题。多元回归分析通过建立因变量与自变量之间的数学模型,对建立的数学模型进行假设检验[9],在符合判定条件的情况下,把给定的自变量数值代入回归模型,从而计算出自变量的值。多元回归分析又可分为多元线性回归分析和多元非线性回归分析。由于海洋执法船主尺度的复杂性,本文采用多元非线性回归分析方法,其基本步骤如下。
1)选择合理的回归模型。根据回归分析相关原理,大部分多元非线性回归问题可转化为线性回归问题[10]。线性回归数学模型表达式见式(1)。
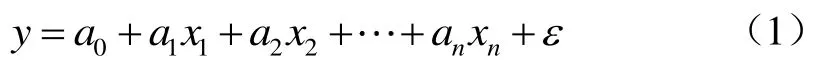
式中:y为因变量;x1,x2,L,xn为自变量;a0,a1,a2,L,an为回归系数;ε~N(0,σ2)为随机因素。
2)回归系数估计。在实际问题中,式(1)中a0,a1,a2,L,an是未知的,需要根据样本观察值给出相应的估计值。因此大量准确的样本资料收集,是得到高拟合度回归模型的前提。回归系数的估计值可通过最小二乘法估出,即回归系数的值应使因变的预测值与真实值的误差向量达到最小。
3)模型检验。数学模型建立后,需要通过数理统计进行检验,检验模型是否与实际数据有较好的拟合度,判断模型线性关系的显著性。常用的统计检验有R检验、F检验和t检验等[9]。本文采用F检验和t检验。其中,F检验用于检验模型整体回归关系的显著性,t检验用于检验模型中各个回归系数的显著性。
2 资料收集
收集大量有效的船型样本是保证回归分析顺利进行的前提。本文收集到国内外海洋执法船共100艘,吨位从100吨位到8 044吨位,包含了典型的中小型船舶以及大型船舶。国外的样本大多数取自韩国、日本和美国并以中型、大型船舶为主。各分段吨位内样本数量的分布状况如图1所示。由图1分析可知,总吨位为400~1 600的船舶数量较多,可知样本中的中型船舶数量较多,而小型和大型海监船和渔政船的数量相对较少。

图1 样本船吨位分布图
3 海监船、渔政船主尺度多变量回归分析
在第2章节中所述样本的基础上,分别以排水量和总吨位为因变量,以船舶主尺度包括垂线间长、型宽和型深,建立多元回归模型。选定了式1中的5个数学模型作为研究基础,分别对二阶多项式、三阶多项式以及对数模型采用向后排除法进行了详细的多元线性回归分析,即将所有自变量均加入模型中,并对模型进行F检验和系数的T检验。根据t检验结果,从模型中剔除因变量影响相对较小的自变量,再次进行回归分析,以此类推。每次都保留比前一次分析更好的模型。对每一个公式都进行T检验和F检验,计算出各个系数的P-value值进行比较。

3.1 排水量与垂线间长、型宽的回归分析
以排水量为因变量,垂线间长和型宽为自变量,建立回归模型。如式(2)~式(4)所示,y为排水量Δ,x1为垂线间长Lbp,x2为型宽B。式(2)是以二阶多项式为基础的回归公式,式(3)是以三阶多项式为基础的排水量与垂线间长、型宽的回归公式。式4是以x1、x2、lnx1、lnx2、x1-1、x2-1、x11/2、x21/2的组合为基础的排水量与垂线间长、型宽的回归公式。

3.2 总吨与垂线间长、型宽、型深的回归分析

以总吨为因变量,垂线间长、型宽和型深为自变量,建立回归模型,如式(5)~式(8)所示。式中y为总吨位GT;x1为垂线间长Lbp;x2为型宽B;x3为型深D。式(5)是以二阶多项式为基础的总吨与垂线间长、型宽、型深间的回归公式。式6是以三阶多项式为基础的总吨与垂线间长、型宽、型深的回归公式。式(7)是以lnx,x-1为基础总吨与垂线间长、型宽、型深的回归公式,式8是以lnx为基础的总吨与垂线间长、型宽、型深的回归公式。

3.3 多变量回归结果总结
根据数理统计知识,回归公式的相关系数越接近1,说明模型的拟合效果越好,而P-value值是F检验结果的体现:一般各个系数的P-value越小,说明各个系数的拟合效果越好,一般只要<2,则认为符合要求。由上述内容可知,以多变量为基础的回归公式,其相关系数均>0.9,P-value值则基本接近于0,说明基于多变量的回归分析达到了较好的效果。从船舶设计经验的角度而言,船舶设计本身是一个综合考虑各项因素的螺旋设计过程,适当增加考虑的因素,更有利于提升船舶的综合水平。
4 结论

本文以100艘国内外海洋执法船的船型资料为样本,采用多元回归分析方法,选取5种典型回归模型,对样本主尺度进行了多元回归分析。建立了以多变量为基础的数学模型,分析比较了总吨位或排水量与主尺度之间的关系。通过F检验和t检验,验证了模型具有良好的拟合效果。提供了多种形式的多变量回归公式供设计时选择,为海洋执法船的初步设计提供了参考依据。

