入水参数对“水漂式”航行体跨介质运动影响数值仿真分析

刘 祥，李天雄，李 林，孙宇新

(南京理工大学瞬态物理国家重点实验室, 南京 210094)

0 引言

“水漂式”跨介质航行体主要利用了物体入水的忽扑现象。顾建农[1]对忽扑现象的描述为：对于轴对称细长体,当作用于其鼻部的水动力不通过其重心的时候,就发生俯仰角速度的变化。形成机理是斜入水时其下部会产生一个细长的空泡,高速侵水过程中,空泡内的压力低于大气压力,形成低压力,造成入水时所受力矩不平衡,从而导致入水后姿态发生较大变化。猛烈的忽扑会使航行体出现穿出水面的轨道。航行体重心位于前部，使得航行体在出水飞行过程中向下低头，再次斜入水并产生忽扑。借助以上原理，跨介质航行体在水面上下波动，所以被称为“水漂”。水漂式跨介质航行体通过在水面反复上下运动，能有效增强隐蔽性与航程。

跨介质航行体的入水到出水的运动过程非常复杂，入水和出水运动涉及介质突变及液体与固体的运动耦合，跨介质航行体的头部结构、入水速度以及入水角度对其空泡及弹道特性有重要影响。Logvinovich[2]基于独立膨原理分析了入水空泡演化规律，为空泡壁运动的研究提供了理论基础。肖海燕等[3]使用Fluent对航行体高速小角度入水进行了仿真，分析沾湿对流体动力及运动姿态的影响，验证了航行体的不对称沾湿是入水失稳的重要原因。朱珠等[4]采用流场与弹道耦合算法对回转体在推力作用下的较小角度入水问题进行了研究。宋武超等[5]针对回转体低速倾斜入水过程空泡的生成机理和演化特性开展研究，研究了入水速度和入水角度对入水空泡、回转体速度、俯仰角及阻力系数的影响规律。杨衡等[6]针对航行体低速入水空泡, 通过试验对比分析了入水速度、入水角度对入水空泡的影响。路丽睿等[7]研究了头型对低速倾斜入水空泡及弹道特性的影响，得出了锥角形航行体在入水后能保持较好稳定性的结论。马庆鹏[8]研究了航行体不同头型、密度、后体长度、直径等参数对入水空泡形态发展、空泡扩张规律以及多相流场分布的影响，并给出了上述各参数对头部压力载荷的影响规律。胡青青[9]对不同头型的钝体以不同倾斜角入水产生空泡流这一过程进行了观察，分析了不同工况下空泡产生和发展的规律。目前对于忽扑的机理认识还不清晰,具体影响因素不明确,缺少定量的研究分析结果。因此，以上研究的重点在于航行体入水后的运动情况，不涉及因强烈忽扑导致的航行体入水后的再出水现象及反复跨介质运动。

本文基于“水漂式”跨介质航行体，通过使用AUTODYN软件对航行体入水过程中进行模拟，分别设计了3种入水角(9°，12°，15°)以及3种入水速度(100 m/s，200 m/s，300 m/s)，不同入水角与入水速度组合共计9种工况，结合仿真结果验证了“水漂式”跨介质航行体入水穿出水面弹道实现的原理及可行性，并分析了入水角度、入水速度对出水角度、运动速度及空泡的影响。

1 数值仿真方法

1.1 仿真模型

本文研究对象的几何结构如图1所示。主要包括航行体头部、航行体身部及固定侧翼，头部长度37.5 mm，身部长度105 mm，内部装有配重块控制身部重心，位于前部，使得航行体在飞行过程中向下低头。楔形头部用于入水时在上下表面产生流速差，进而产生升力使航行体向上偏转，在水面发生弹跳。两边侧翼用于维持航行体左右平衡，在入水后维持稳定。本文研究对象的入水示意图如图2所示。

计算水域长1.2 m，宽0.045 m，深0.335 m，初始时刻航行体轴线与水平面夹角为入射角，初始时刻水平方向速度沿X轴负方向，铅垂方向速度沿Z轴负方向。

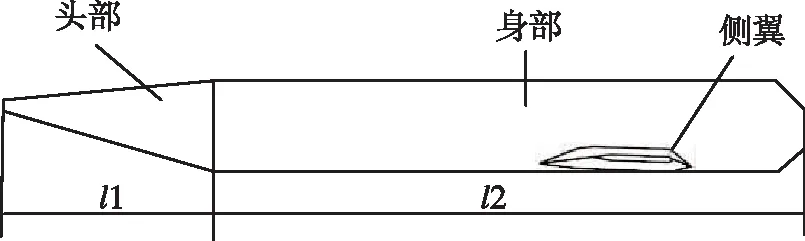
图1 “水漂式”跨介质航行体模型示意图Fig.1 Simulation model of the “water drifting” aerial-aquatic vehicle

图2 “水漂式”跨介质航行体入水示意图Fig.2 Diagram of “water floating” aerial-aquatic vehicle entering water

1.2 计算模型

由于涉及流体与固体的相互作用，因此流固耦合数值模拟采用AUTODYN-3D拉格朗日-欧拉耦合技术，对如表1所示的3种入水速度和3种入水角度的航行体入水进行研究。航行体采用拉格朗日建模，水采用欧拉建模。整体模型如图3所示，航行体部分网格如图4所示。

表1 入水角度及速度Tab.1 Water entry angle and speed of “water drifting” aerial-aquatic vehicle

图3 “水漂式”跨介质航行体入水流域仿真模型示意图Fig.3 The flow field of the “water drifting” aerial-aquatic vehicle penetrating into water

图4 航行体及部分水域网格示意图Fig.4 Grid of aerial-aquatic vehicle and water

1.3 水的状态方程

水的SHOCK状态方程为

P=PH+Γρ(e-eH)

(1)

式中，PH和eH分别为材料冲击Hugoniot态的压力和比动能，Γ为Gruneisen系数。

假设Γρ=Γ0ρ0=常数，且

(2)

式(2)为冲击波关系式,式中ρ0和c0分别为材料初始密度和声速，μ为材料的压缩比，λ为冲击 Hugoniot 参数。λ和c0为常数,由以下冲击波实验关系式确定

D=λu+c0

(3)

式中，D为冲击波速度,u为波后质点速度。取ρ0=0.998 g/cm3,C0=1.647×103m/s,λ=1.921，Γ=0。

1.4 航行体的材料状态方程及强度模型

头部和身部材料均采用SHOCK状态方程、Johnson-Cook强度模型。为控制航行体重心位置，头部采用STEEL S-7，身部采用AL 7039，两种材料的SHOCK状态方程参数如表2所示。

表2 身部材料的SHOCK状态方程参数Tab.2 SHOCK equation of state parameters of the aerial-aquatic vehicle body material

Johnson-Cook 屈服应力为

(4)

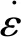
两种材料的Johnson-Cook强度模型参数如表3所示。

表3 身部材料的Johnson-Cook强度模型参数Tab.3 Johnson-Cook strength model parameters for aerial-aquatic vehicle body materials

1.5 仿真方法验证

为了验证数值计算的可靠性，对郭子涛[10]实验研究的平头圆柱垂直入水问题进行数值模拟计算,实验采用的平头圆柱长为25.4 mm，直径12.56 mm，质量为25.1 g，初速度为397 m/s。计算采用AUTODYN的欧拉-拉格朗日流固耦合算法,身部采用STEEL S-7材料，水采用SHOCK状态方程。对比实验结果与仿真结果入水后的侵彻位移和速度衰减随时间的变化，如图5所示。可以看出，仿真结果和实验结果吻合良好，有效地验证了数值模拟的正确性。

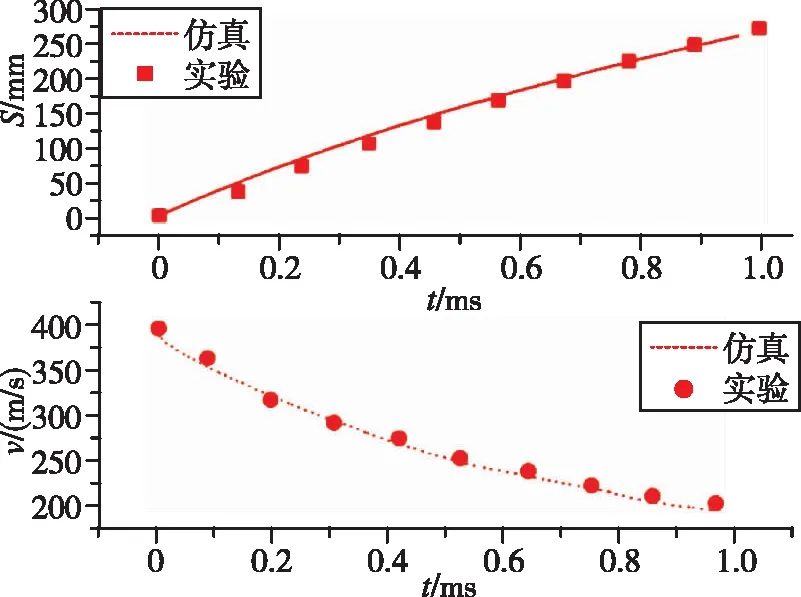
图5 平头圆柱位移与速度变化曲线Fig.5 Displacement and velocity of the flat head cylinder

2 结果分析

对跨介质航行体在入水速度100 m/s，200 m/s和300 m/s，入水角度为9°，12°和15°情形下的运动过程和速度变化、出水角度进行了分析。

2.1 运动过程分析

图6 入水速度300 m/s，入水角度15°航行体三维空间入水轨迹Fig. 6 Trajectory of the aerial-aquatic vehicle with water entry speed of 300 m/s and angle of 15°

图6为入水速度300 m/s，入水角度15°的航行体在三维空间的入水轨迹。图中显示入水空泡经历了入水撞击、空泡形成和开空泡阶段。航行体撞击水面时航行体上下表面与水的接触面积不同，即沾湿面积不同。这使得航行体传递给流体质点的动能不一样，形成不对称的空泡，航行体下表面的空泡发展快于上表面，进而产生流速差，形成上升力使航行体向上偏转,航行体由入水姿态转为出水姿态。同时可以看到,航行体侧翼划水产生的小空泡，侧翼处产生额外的升力使航行体保持平衡，防止在铅锤方向发生偏转。

图7为入水速度300 m/s，入水角度9°的航行体在三维空间的入水轨迹,对比入水速度为300 m/s时，入水角9°和15°的空泡图。随着航行体入水角减小，在入水时航行体下表面沾湿面积增大，同时上表面沾湿面积减小。在相同入水速度下，小角度入水的航行体下表面传递给流体质点的动能更大，因此航行体获得的升力更大，更早转变为出水姿态。

图8为入水速度100 m/s，入水角度15°的航行体在三维空间的入水轨迹。对比入水角15°，入水速度为100 m/s和300 m/s时的空泡图。随着速度增大，航行体传递给流体质点的动能更大，因此空泡发展更快，速度差产生的升力同样增大。但由于初始速度较大，入水速度300 m/s的航行体转变为出水姿态所需时间仍长于入水速度100 m/s的航行体，同时受到的水阻力也更大。

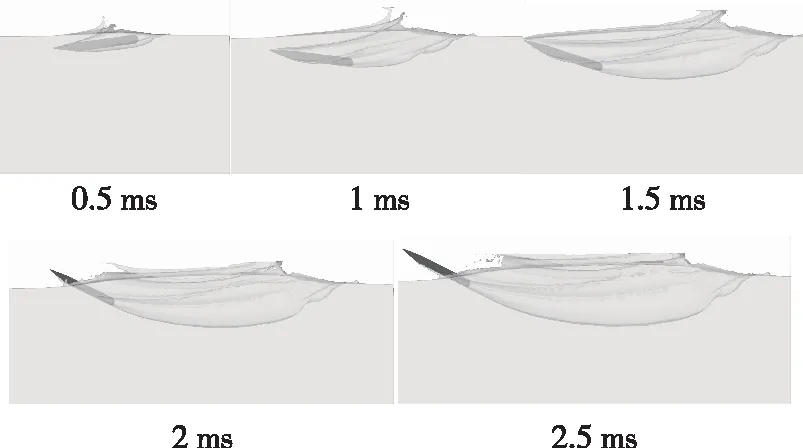
图7 水速度300 m/s，入水角度9°航行体三维空间入水轨迹Fig.7 Trajectory of the aerial-aquatic vehicle with water entry speed of 300 m/s and angle of 9°

图8 水速度100 m/s，入水角度15°跨介质航行体三维空间入水轨迹Fig.8 Trajectory of the aerial-aquatic vehicle with water entry speed of 10 m/s and angle of 15°

将9种工况下航行体从入水到偏转出水的运动轨迹进行对比，如图9所示。可以看出,航行体轨迹在入水后先近似保持直线，之后逐渐向上偏转。在相同入水速度下，随着入水角度增大入水深度增加，航行体的偏转程度加剧。在相同入水角度下，随着入水速度增加，入水深度同样加深。在入水角为9°时，入水速度对入水弹道的影响较为明显。而在入水角为12°和15°时，航行体速度超过200 m/s后的弹道近似，速度对弹道的影响减弱。9种工况的具体入水深度及出水水平距离如表4所示。

图9 9种工况航行体的入水轨迹Fig.9 Trajectories of aerial-aquatic vehicle in nine working conditions

表4 航行体入水深度及出水距离Tab.4 The depth and distance of the aerial-aquatic vehicle after left water

2.2 速度分析

在仿真模型中，航行体在入水前垂直于水面的速度如图10所示，分量指向Z轴负向，整个入水阶段头部与尾部垂直于水面的速度分量都为负值。当两者数值都转化为正值，说明航行体开始进入出水阶段。以头部与尾部垂直于水面的速度分量转化为正值的时刻为出水阶段开始时刻。

航行体出水阶段开始时刻、出水时刻如表5所示。对比表中数据，入水角度增大会使航行体出水时间变长。在相同的入水角度下，出水时间随着入水速度加快而缩短。

图10 入水角度9°，入水速度100 m/s的航行体Z方向速度分量Fig.10 Z-direction velocity component of the vehicle with a water entry angle of 9° and a water entry velocity of 100 m/s

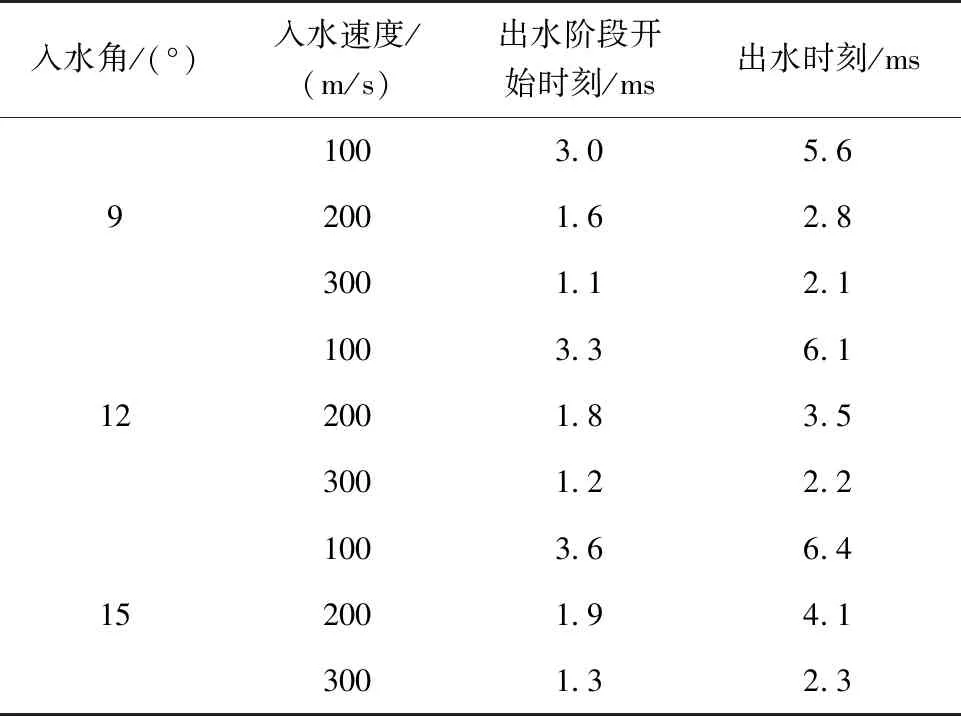
表5 航行体出水阶段开始时刻、出水时刻表Tab.5 The starting time of leaving water and the time of left water

观察速度曲线(图11～14)可以发现，航行体入水后，由于水阻力的影响，在入水阶段动能不断降低，速度下降。在出水阶段初期速度仍然有所下降，之后速度相对稳定。进一步对比不同入水速度的变化曲线，入水速度增大，航行体入水的深度增大，水下运动距离增长，且随着速度增大，阻力增大，阻力与运动方向相反，动能损失与速度损失的增大。

通过对比相同速度下不同入水角度的速度变化曲线，结合弹道图对比可以发现，随着入水角度增大，航行体入水的深度增大，动能损失与速度损失随之增加。具体速度损失量如表6所示，分析发现，入水速度对速度损失的影响强于入水角的影响。

表6 航行体出水速度Tab.6 Velocity difference of the aerial-aquatic vehicle in nine working conditions

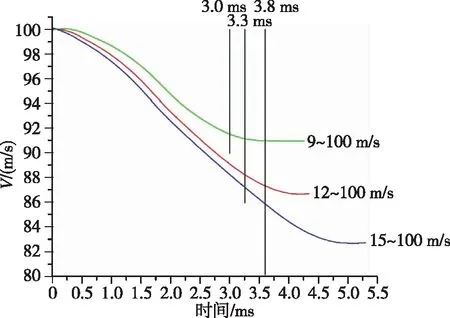
图11 入水速度100 m/s的航行体速度曲线Fig.11 The velocity of the aerial-aquatic vehicle at a water entry velocity of 100 m/s

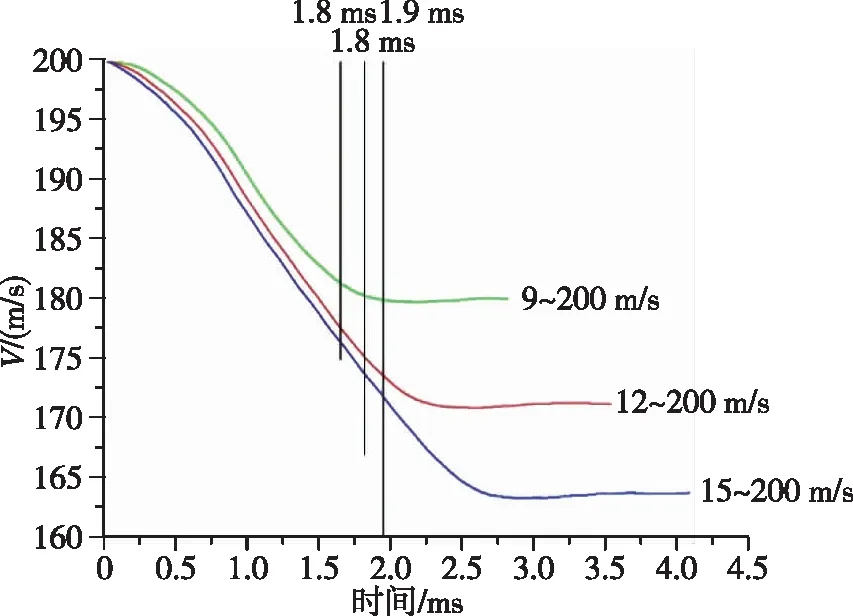
图12 入水速度200 m/s的航行体速度曲线Fig.12 The velocity of the aerial-aquatic vehicle at a water entry velocity of 200 m/s

图13 入水速度300 m/s的航行体速度曲线Fig.13 The velocity of the aerial-aquatic vehicle at a water entry velocity of 300 m/s

图14 9种工况速度曲线Fig.14 The velocity of aerial-aquatic vehicle in nine working conditions

2.3 出水角分析

航行体的俯仰角随时间变化曲线如图15～20所示。在撞击水面前，航行体的俯仰角近似不变，之后俯仰角逐渐减小，在航行体下表面沾湿后，俯仰角的变化加快，到最后俯仰角由正变负，说明航行体此时已经发生抬头弹跳。

图15 入水角9°航行体俯仰角随时间变化曲线Fig.15 The pitch angle curve of the aerial-aquatic vehicle at a water entry angle of 9°

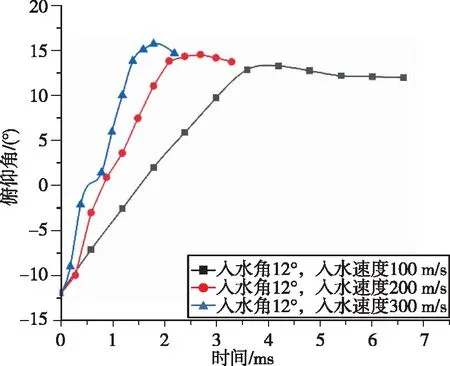
图16 入水角12°航行体俯仰角随时间变化曲线Fig.16 The pitch angle curve of the aerial-aquatic vehicle at a water entry angle of 12°

图17 入水角15°航行体俯仰角随时间变化曲线Fig.17 The pitch angle curve of the aerial-aquatic vehicle at a water entry angle of 15°

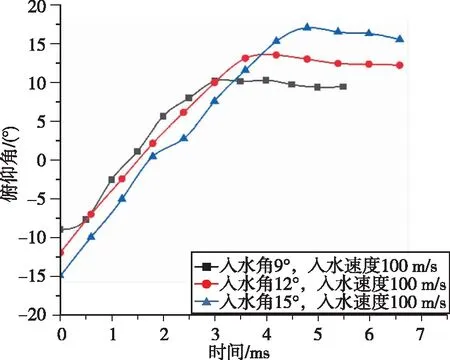
图18 入水速度100 m/s航行体俯仰角随时间变化曲线Fig.18 The pitch angle curve of the aerial-aquatic vehicle at a water entry velocity of 100 m/s

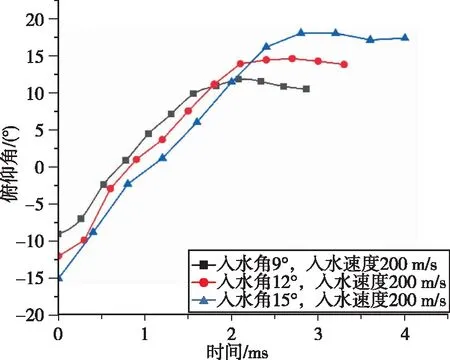
图19 入水速度200 m/s航行体俯仰角随时间变化曲线Fig.19 The pitch angle curve of the aerial-aquatic vehicle at a water entry velocity of 200 m/s

图20 入水速度300 m/s航行体俯仰角随时间变化曲线Fig.20 The pitch angle curve of the aerial-aquatic vehicle at a water entry velocity of 300 m/s

航行体出水角度如表7所示。由表7做不同入水速度及不同入水角对应的出水角曲线如图21，22所示。在同一入水速度下，随着入水角增大垂直于水面方向的速度分量增大，同时航行体由上下表面流速差获得的升力减小，使得航行体入水深度加深，入水阶段所需时间更长，航行体平行于水面方向的速度损失随着入水角增加而增大。进而导致出水角随入水角增大而增大，即入水速度一定时，入水角增加，航行体入水后的向上偏转趋势增加。

表7 航行体出水角度表Tab.7 Water outlet angle

图21 不同入水速度航行体出水角曲线Fig.21 Curve of outlet water angle of aerial-aquatic vehicle with different water entry speed

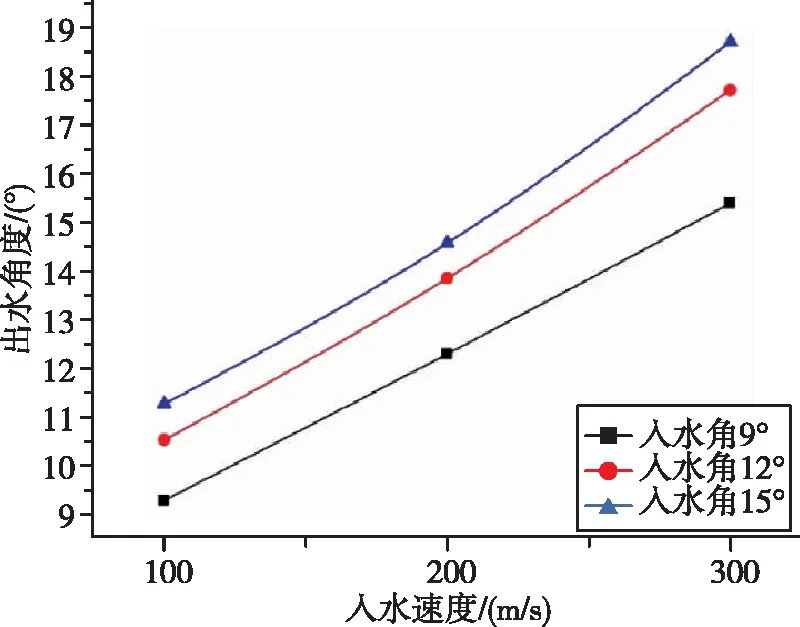
图22 不同入水角度航行体出水角曲线Fig.22 Curve of outlet water angle of aerial-aquatic vehicle with different water entry angle

在同一入水角度下，随着入水速度增大垂直于水面方向的速度分量增大，航行体入水深度加深,入水阶段所需时间更长，航行体平行于水面方向的速度损失随着入水速度增加而增大,进而导致出水角随入水速度增大而增大，即入水角一定时，入水速度增加，航行体入水后的向上偏转趋势增加。

3 结论

本次仿真初步验证了跨介质航行体功能实现的可行性，同时分析了入水角度与入水速度的航行体运动过程中速度变化及出水时速度与角度的影响。

1)航行体入水撞击水面时，上下表面与水的接触面积不同，这使得航行体上下表面传递给流体质点的动能不同，形成不对称的空泡，航行体下表面的空泡发展快于上表面，进而产生流速差形成上升力使航行体向上偏转,航行体由入水姿态转为出水姿态。

2)在同一入水速度下，随着入水角度的增加，航行体下表面与水接触面积减小，上表面与水接触面积增大。在相同入水速度下，小角度入水的航行体下表面传递给流体质点的动能更大，因此航行体获得的升力更大，更早转变为出水姿态。同时由于受水阻力影响，时间也随着入水角度增加而加长，导致动能与速度的损失增大。

3)在同一入水角度下，随着入水速度的增加，航行体传递给流体质点的动能更大，因此空泡发展更快，速度差产生的升力同样增大。但由于初始入水速度高，航行体入水深度加深,入水阶段所需时间更长，受水阻力影响的时间也随着入水角度增加而加长，导致动能与速度的损失增大。

4)入水角与入水速度的增加都会增加航行体入水后的向上偏转趋势以及最终出水的出水角，而其中入水速度对出水角的影响更为明显。