跨介质航行器波浪环境入水流场演变和运动特性研究

2020-06-15史崇镔张桂勇孙铁志宗智

宇航总体技术 2020年3期

史崇镔，张桂勇,2,3，孙铁志,2，宗智,2,3

(1.大连理工大学船舶工程学院，大连 116024；2.大连理工大学工业装备与结构分析国家重点实验室，大连 116024；3.高新船舶与深海开发装备协同创新中心，上海 200240)

0 引言

水空两栖跨介质航行器是航空科学家和工程师结合飞行器和潜艇的优势而发明的一种可以实现水空两栖作业的航行器，最初的设想是军事上用于实现紧急情况下的突防，后来随着概念和技术的发展出现了更多将此两栖航行器用于民用领域的设计方案[1]。跨介质航行器通过集中两种平台的优点和操作模式，可显著增强军队执行沿海快速、隐秘的插入式作战任务的能力[2]。本文基于仿生学原理，提出一种新型跨介质航行器，通过对其入水过程进行试验和数值模拟研究，分析了在其跨介质航行时的动力学特性和入水空泡演变过程，为跨介质航行器的设计和应用提供了参考。

国外研究方面， 2008年10月，DAPRA提出了一种混合飞行平台，该平台融合了飞机的速度和航程，水面舰艇的巡弋能力以及潜艇的隐身能力，该“潜水飞机”可以在5级海况下在水面或水下巡弋3天，该项目虽未能取得实质性进展，但提出了一种未来海上作战新模式[3]。2010—2014年，Lock等[4-5]研究了一种可应用于潜水无人机的多模式仿生翼。他们的研究首次对适应两栖环境的仿生驱动结构的水空运动模型进行了分析，为跨介质航行器的实现提供了理论支撑和经验借鉴。2011年，Gao等[6]从游动理论、机构设计、驱动方式和控制方式等方面展开研究，提出了一款水空两栖作业的仿飞鱼机器人样机。2015年，Israelevitz等[7]提出了一种用于水质采样的水空两栖多模式仿生样机概念。2016年，Siddall等[8]设计了一种桨式推进仿鲣鸟两栖航行器，成功实现了从水中到空中的过渡，同时采用鲣鸟溅落式入水实现空气到水体的转换。

国内研究方面，2015年，邢文中等[9]对海空无人机的气动水动布局进行设计和分析，为跨介质航行器设计布局提供了参考和借鉴。2014年，吝科等[10]通过数值模拟分析了升力型航行器飞行时和潜航时的动力特性。2015年，杨海燕等[11]研究了雷诺数对航行器流体动力学特性的影响，探索其适应不同介质环境的航行能力。2016年，廖保全等[12]提出了跨介质航行器设计方案并研究了其空中气动特性和水下水动特性。2017年，侯昭等[13]对回转体倾斜入水进行了试验与数值计算分析。2018年，路中磊等[14]对开放空腔壳体倾斜入水进行了试验研究。2019年，罗驭川等[15]对截锥体头型航行器入水进行了试验研究。

本文的跨介质航行器结构外形主要基于仿生学原理，空中推进装置安装在机体上部，入水前推进装置的螺旋桨先收进推进器内，随后推进装置整体垂直收入机体内部，同时部分翼体收缩进机体内，其示意图如图1所示。

图1 航行器示意图Fig.1 Schematic of vehicle

本文通过试验与数值计算结合的方式展开研究，通过对跨介质航行器入水进行试验，用高速相机对航行器入水过程进行记录，从而分析航行器入水过程的现象、自身运动特性以及入水空泡的变化。同时用计算流体力学(CFD)方法对试验过程进行数值仿真，物理模型选用k-ε湍流模型、VOF模型和欧拉多相模型等，利用重叠网格方法模拟航行体入水过程，从而建立航行体入水问题数值仿真方法，验证数值方法的有效性后进一步模拟了在有波浪的情况下航行器入水过程，在静水情况的基础上分析了波浪对航行器入水过程的影响。

1 试验装置和数值计算模型

1.1 试验系统

试验装置主要由水箱、支撑架、灯光系统、高速摄像机和计算机组成，其示意图如图2(a)所示。水箱使用钢化有机玻璃制成，长、宽、高分别为1.5,0.8,1.2 m，试验水深为0.7 m；支撑架置于水箱底部，达到支撑和方便移动的目的；灯光系统选用两个Starison CE-1500Ws透射式聚光灯；高速摄像机型号为Phantom v12.1，试验过程采用1280 ×800的分辨率，3000 帧/s的拍摄帧率，通过计算机进行照片采集和处理。航行器模型如图2(b)所示，试验和数值计算均采用右侧变形后航行器模型。

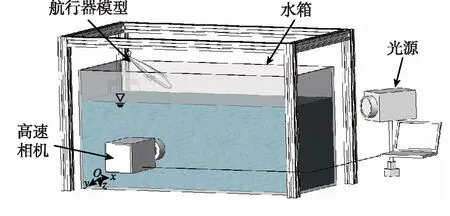
(a) 试验装置示意图

(b) 航行器模型(左为入水变形前，右为入水变形后)图2 试验装置及航行器模型Fig.2 Schematic of the experimental setup and vehicle model

1.2 数值计算模型

1.2.1 基本控制方程

本文计算涉及的控制方程主要包括质量守恒方程和动量守恒方程。

(1)质量守恒方程

质量守恒定律在流体运动中以连续性方程来表达，不可压缩时的微分形式为

(1)

式中，ρ为流体密度，本文涉及气、液两相，故密度根据各相所占体积分数来确定；ui为沿x，y，z方向上的速度分量；xi为在x，y，z方向上的位置。

(2)动量守恒方程

从动量定理出发推导得出的动量方程微分形式为

(2)

式中，P为压力，τij为黏性剪切应力，其表达式为

(3)

式中，μ为动力黏性系数。

1.2.2 湍流模型

本文选取k-ε湍流模型，其微分方程表达式为

(4)

(5)

湍动黏度μt可表示为k和ε的函数

(6)

Pk为黏性力引起的湍动能产生项，其表达式为

(7)

式中，Cε1，Cε2和Cμ为常数，取值分别为Cε1=1.44，Cε2=1.92，Cμ=0.09；σk为k的普朗特数，取值σk=1.0；σε为ε的普朗特数，取值σε=1.3；μ为流体动力黏度；Pkb和Pεb为浮力引起的湍动能产生项。

1.2.3 波浪模型

已有研究表明,采用相同的造波方法时，一、二阶模拟值与一阶理论值相对误差值小于1%[16]，对于本研究问题该误差可以忽略不计。本文使用斯托克斯波理论的一阶近似对波浪建模，生成具有规则周期性正弦分布的波。

水平速度的方程为

uh=aωcos(Κ·x-ωt)eKz

(8)

垂直速度的方程为

uv=aωsin(Κ·x-ωt)eKz

(9)

表面高度的方程为

η=acos(Κ·x-ωt)

(10)

式中，a为波幅值，ω为波频率，Κ为波矢量，上标中的K为波矢量的幅值，z为平均水位的垂直距离。波周期和波长的定义如下

(11)

(12)

一阶波在有限水深d中的耗散关系为

(13)

而对于无限水深，耗散关系为

(14)

波形与深度无关。

针对本文的造波方法，首先在物理模型中设置VOF多相模拟，选择VOF波模型并创建轻流体相和重流体相。随后在波节点中选择一阶波并指定波高、水深、指定类型(波长)以及相应的波长值。最后设置体积分数、速度和压力的初始条件，设置入口边界和出口边界的边界条件，并设置VOF波力。

1.2.4 计算模型及设置

本文采用网格质量较好的切割体网格生成器，加以表面重构提高网格的质量，在航行器壁面设置棱柱层网格生成器。为保证数值计算的质量，在航行器路径、水面以及水面下部分范围内进行网格加密。采用重叠网格技术对航行器的运动过程进行建模，重叠网格就是嵌套于流体域网格中、随物体运动的网格，具有网格易生成、质量好的特点。重叠网格通过搜索指定区域，进行网格划分；在物体运动过程中的每个时间步都需要将重叠区域从流体域内逐步剔除重新定位，以此来模拟航行器入水过程；重叠网格之间通过数据的插值进行信息传递。网格划分时保持航行器重叠区域水平，网格生成后对重叠区域旋转平移到指定工况，局部网格划分如图3所示，最小网格尺寸为1.25 mm。

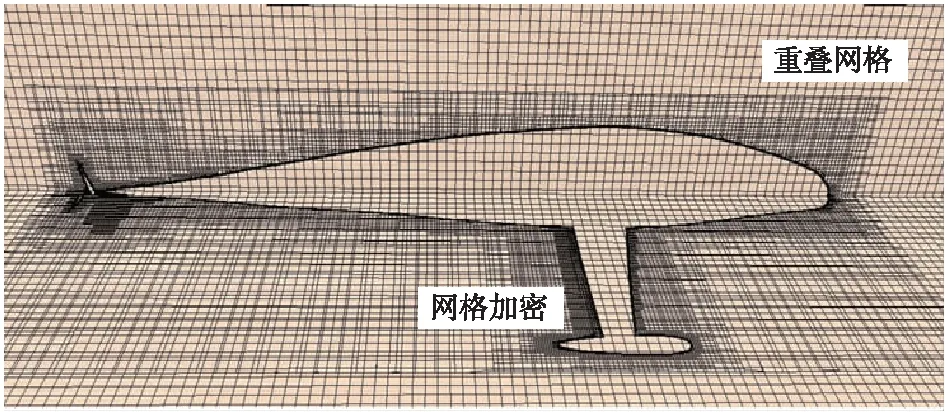
图3 网格划分Fig.3 Mesh generation

航行器模型由3D打印制成，表1给出了入水变形后航行器的尺寸等参数。

表1 航行器参数Tab.1 Vehicle parameters

由于入水问题属于多相流问题，所以采用基于欧拉-欧拉方法的VOF模型进行计算。将多相流中的流体视为均匀物质，通过各相流体所占体积分数来描述不同的流体。体积分数总和为1，体积分数为1时代表全部为液相，为0时代表全部为气相，体积分数在0到1之间表示此时为气液混合物，以此来表征各相流体体积，来模拟航行器入水过程中的空泡演变。计算时采用VOF定义静水波和一阶波来模拟气液交界面，采用一阶隐式求解器进行求解，时间步长为2×10-4s，将边界设置为速度入口，顶部边界设为压力出口；重叠区域设定为重叠网格边界，航行器表面设定为壁面。

2 结果与分析

2.1 数值计算模型评价

图4 航行器初始状态示意图Fig.4 Schematic diagram of the initial state of the vehicle

试验中航行器以2.65 m/s速度、26°入水角的初始条件入水，入水状态示意图如图4所示。o为航行器质心并且为航行器坐标系原点，V为沿机身方向的总速度，vx,vy分别为航行器水平、垂直方向分速度，入水角α为速度V与水平速度方向的夹角，当α在航行器坐标系第一象限时称为为正攻角状态。空泡演变过程如图5(a)所示。由图5(a)可以看出，航行器头部首先进入水中，由于速度较低，在头部没有明显的空泡产生；入水后20～40 ms期间，首部翼体从空气进入水中，浮力的作用会为航行器提供一定升力，俯角逐渐减小；40～60 ms期间，航行器尾部入水，尾翼也会提供一定升力，俯角进一步减小，此时可以看到首部翼体和尾部翼体均产生空泡；随后的时间，航行器继续水平方向航行，机身逐渐与水面平行，首部翼体及机身后半段产生的空泡随航行器运动逐渐拉长；整个过程首部均无空泡产生。

进行数值计算对比时采用与试验相同的工况，通过水体积分数0.5的等值面来表征入水过程中空泡的变化。选取与试验相同的入水时刻进行对比，得到如图5(b)所示的空泡演变过程。由图5(b)可以看出，数值计算得到的航行器入水轨迹与空泡形态演变与试验结果一致性较好，能够较为准确地得到入水空泡的形成及发展，从而验证了所用数值模型的准确性。

(a) 试验空泡演变过程

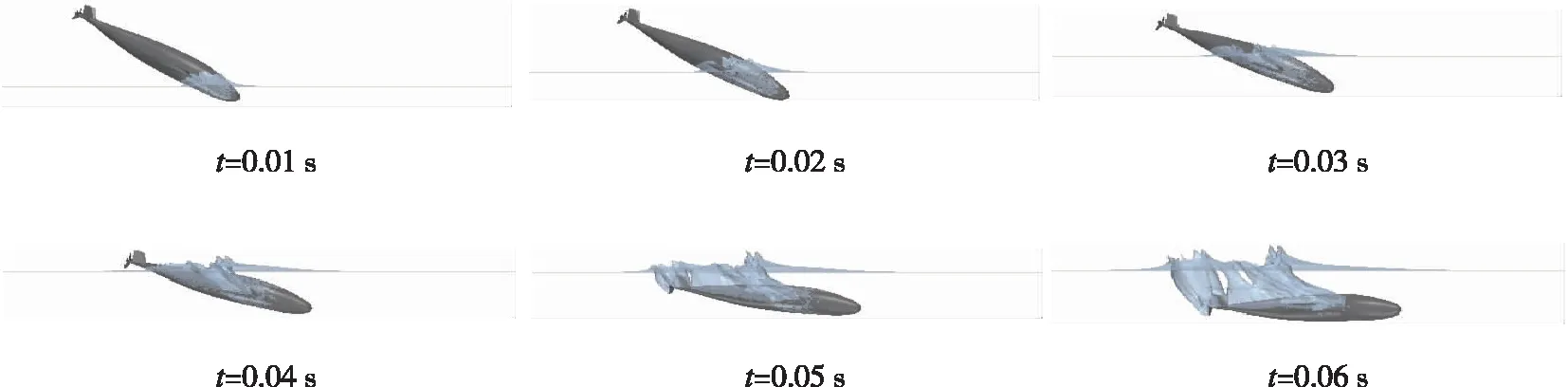
(b) 数值计算空泡演变过程图5 入水过程空泡形态演变试验和数值预报对比Fig.5 Comparison of cavity evolution between the experimental results and numerical predictions

2.2 波浪条件影响分析

本节主要研究了静水工况和有波浪工况下航行器入水过程空泡演变和运动特性，二者采用的物理模型和计算水域均与试验相同(有限水深)，选取波浪参数为：波长0.6 m，波高0.02 m，周期0.62 s，波浪前进方向与航行器水平速度正方向相同。图6分别给出了两种工况下入水空泡演变过程，选取与水接触时刻为时间零点。从图6中可以看出，整个入水过程航行器头部均无空泡产生，入水空泡演变规律相同。通过对比可以看出，波浪的存在会对航行器姿态产生一定影响，静水情况下航行器在0.05 s时仍有明显的俯角，而有波浪的情况下航行器与水平面的夹角很小，将更快达到水平航行状态。

(a) 静水工况空泡演变过程

(b) 波高0.02 m工况空泡演变过程图6 有无波浪条件下入水过程空泡形态演变对比Fig.6 Comparison of cavity evolution with and without waves

为了进一步探究航行器的运动特性，对航行器入水过程中速度、加速度、运动轨迹以及升阻力系数进行提取与分析。图7给出了入水过程水平和垂直方向速度、加速度变化曲线。从图7(a)和7(b)中可以看出，在航行器头部(航行器最前端部分，翼体属于航行体的一部分，由于其可变形的特点，因此与传统机翼有一定区别，在飞行过程中翼体也可称为航行体机翼)与水接触之后的一段时间内，有无波浪两种工况航行器的水平和垂直速度变化几乎一致。在0.025 s时刻左右，两种工况出现差异，在波浪的作用下，由于波浪前进方向与水平速度正方向相同，所以航行器的水平速度增长大于无波浪的情况，航行器尾部螺旋桨在0.05 s附近完全进入水中，阻力瞬时增大，速度曲线会出现突然降低又上升的趋势。在0.03 s左右，翼体从空气进入水中，在升力与浮力的作用下使垂直方向速度降低，带波浪工况下航行器稳定后的垂直速度始终小于静水工况。由于航行器没有推进装置，入水稳定后在阻力和浮力的作用下水平速度和垂直速度均逐渐降低。

从图7(c)和7(d)中可以看出，由于航行器的特殊结构，在入水后会产生一定的正向水平加速度，在波浪的推动下带波浪工况的水平加速度大于静水工况，0.03 s时由于翼体进入水中，水对航行器的作用面积突然增大，水平加速度达到最大值，随后加速度逐渐减小，在尾部尾翼入水时也会产生相同的加速度突变。垂直加速度变化规律与水平加速度的规律大致相同，但入水初期带波浪情况下航行器具有更大的反向加速度，在尾部翼体入水时加速度突变峰值小于静水工况。

(a)水平速度

(b)垂直速度

(c)水平加速度

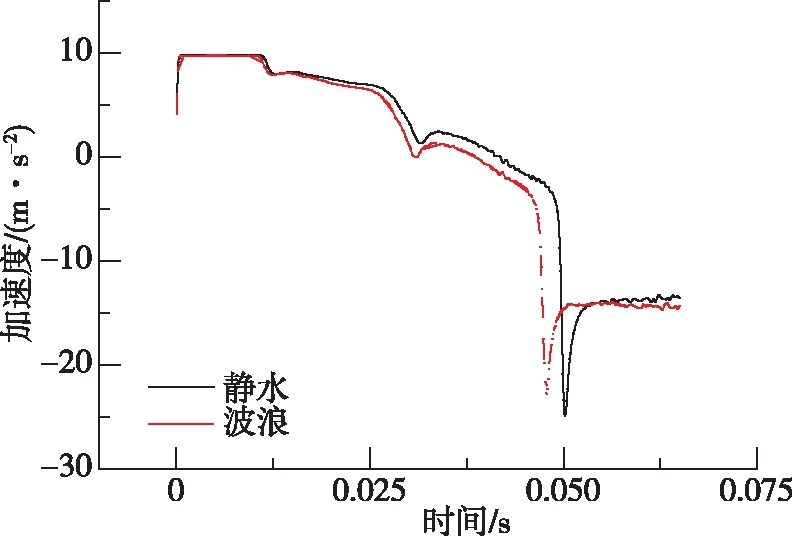
(d)垂直加速度图7 静水和波浪条件下速度、加速度变化对比Fig.7 Time histories of velocity and acceleration evolution under still water and wave conditions

图8给出了水平与垂直方向位移的曲线对比。可以看出，两种工况下航行器入水过程水平和垂直位移均呈近似线性增加变化。从图8(a),(b)可以看出，在入水前及入水后一段时间内，两种工况具有几乎相同的水平和垂直位移；在0.03 s后，由于波浪的作用二者位移变化产生差异，有波浪的工况水平方向和垂直方向位移始终大于无波浪工况。

(a) 水平位移

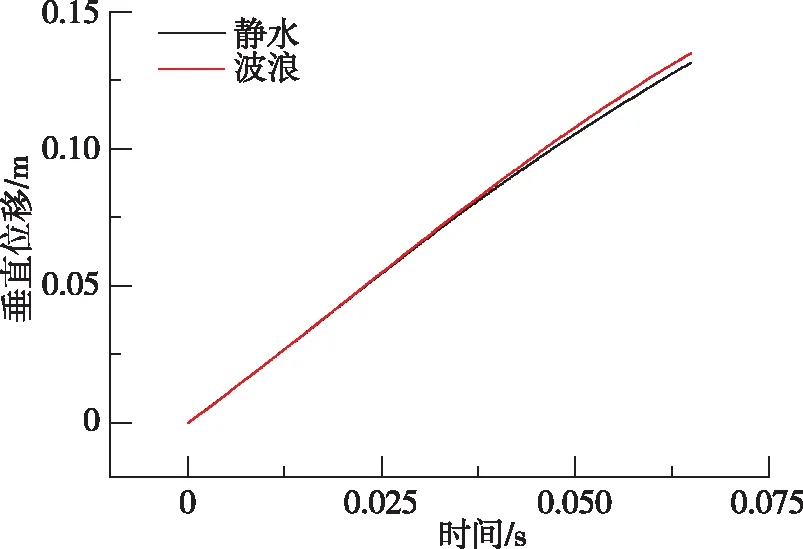
(b) 垂直位移图8 静水和波浪条件下位移变化对比Fig.8 Time histories of displacement evolution under still water and wave conditions

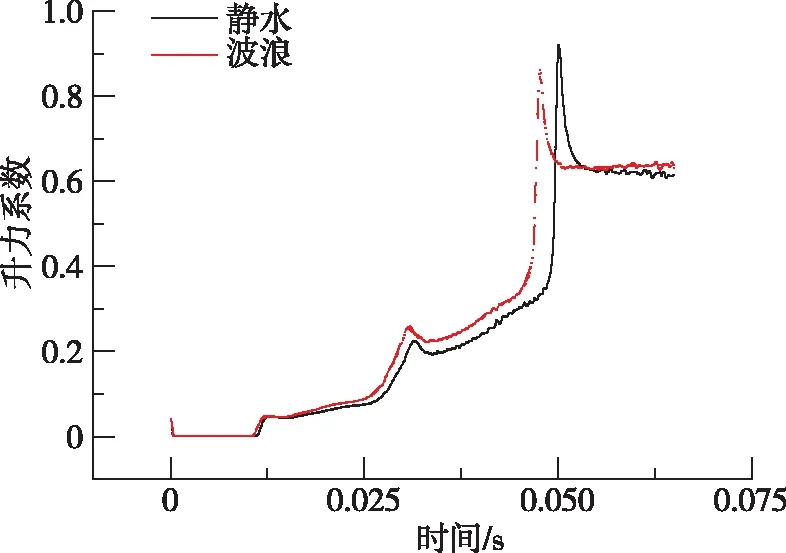
(a) 升力系数

(b) 阻力系数图9 静水和波浪条件下升力、阻力系数曲线Fig.9 Time histories of lift coefficients and drag coefficients under still water and wave conditions

进一步对航行器的升力、阻力系数进行对比分析，图9给出了航行器的升力、阻力系数曲线。由于升力、阻力系数与垂直和水平方向加速度具有密切的关系，从图9中可以看出，升力、阻力系数曲线的整体变化趋势与加速度的相反数变化趋势相同。在尾部翼体入水前这段时间内，带波浪的工况航行器始终受到更大的升力，尾部翼体入水时静水工况会产生更大的升力系数峰值。由于波浪的推动作用，入水初期带波浪工况航行器所受的阻力较小，首部翼体完全入水后阻力降到最小值，与水平加速度曲线进行对照可以看到此时水平加速度值最大，在入水稳定后，可以看出波浪对航行器受到的阻力没有明显影响，其所受升力略大于静水工况。

2.3 波高影响分析

本节主要研究了不同波高情况下航行器入水过程空泡演变和运动特性，采用的物理模型和计算水域均相同，波长均为0.6 m，波高分别选取0.02 m和0.03 m，波浪前进方向与航行器水平速度正方向相同。图10给出了两种工况入水过程空泡演变过程。可以看出，从航行器头部入水到翼体接触水面这段时间内没有产生空泡，飞行姿态变化不明显；翼体入水后会产生空泡，在升力的作用下航行器俯角有明显减小，随着机身进入水中，升力逐渐增大；尾部翼体进入水中后同样也会产生明显的空泡，此时航行器姿态逐渐与水平面平行。通过两波高工况航行器入水过程对比可以看出，两种情况空泡演变过程整体特征基本相同，但是当波高较大时，入水过程产生的空泡非定常性较强。

(a) 波高0.02 m工况空泡演变过程

(b) 波高0.03 m工况空泡演变过程图10 不同波高入水过程空泡形态演变对比Fig.10 Comparison of cavity evolution in different wave heights

为了进一步探究航行器的运动特性，对航行器入水过程中速度、加速度、运动轨迹以及升阻力系数进行提取与分析。图11给出了航行器的速度和加速度曲线，从速度曲线可以看出，航行器入水后的一段时间内，水平和垂直方向速度均有增加，0.025 s时翼体完全入水后，垂直速度变得平稳，0.045 s尾部翼体进入水中后，水平、垂直方向速度均开始降低。从图11(a)和(c)中可以看出，0.03 m波高情况水平方向的速度、加速度变化落后于0.02 m波高情况，但具有更大的速度和加速度峰值；从图11(b)和(d)中可以看出， 0.03 m波高垂直方向加速度的变化同样稍有滞后，加速度峰值略小，所以该情况下垂直速度略大于0.02 m波高。

(a) 水平速度

(b) 垂直速度

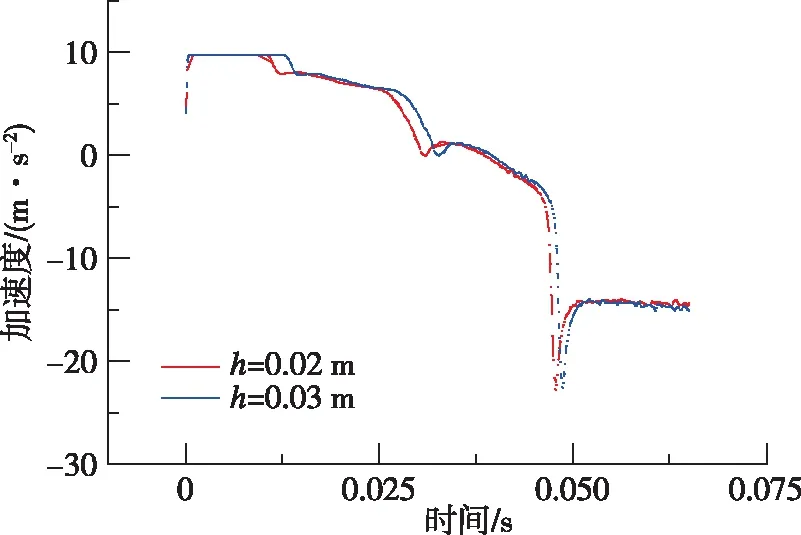
(d) 垂直加速度图11 不同波高入水过程速度和加速度对比Fig.11 Comparison of velocity and acceleration in different wave heights

图12给出了两种工况下航行器水平位移和垂直位移的曲线。两种波高航行器入水过程水平和垂直方向位移均近似线性变化。通过图12(a)、(b)可以看出，由于水平速度、加速度变化的滞后，即使在0.03 m波高工况具有更大的加速度和速度，水平方向的位移也与0.02 m波高工况几乎相同；垂直位移略大于0.02 m波高工况。

(a) 水平位移

(b) 垂直位移图12 不同波高入水过程位移变化对比Fig.12 Comparison of displacement in different wave heights

图13为航行器入水过程的升力、阻力系数曲线。在航行器完全入水前的过程中，受到的升力逐渐增大，并在前翼体和后翼体入水时出现升力的突变，后翼体入水时，升力达到整个过程的最大值，随后下降到一个大于0的稳定值。从图13(b)可以看出，在后翼体入水前航行器受到一个负方向的阻力，即有正向加速度，翼体入水时阻力系数会突然变小，机身完全入水后，阻力系数变为正值并逐渐增大，航行器开始减速。从图13(a)中曲线对比可以看出，由于波高的不同，航行器头部与水接触的时间会出现一些差异，0.03 m波高工况升力系数的变化规律与0.02 m波高工况相同，升力系数幅值相同。从图13(b)中曲线对比可以看出，0.03 m波高工况航行器入水在水平加速的阶段阻力系数峰值小于0.02 m波高工况，之后的减速稳定阶段阻力系数也始终小于0.02 m波高工况。