分析差异探索解题思路
2020-06-13赵陈成
赵陈成
从辩证法的观点看,每一道数学题,实质上都存在题设和结论之间的一对矛盾.解题的过程是分析题设与结论之间的差异,寻找内在联系,逐步缩小差异,最后达到解决矛盾的目的.因此,在日常的教学活动中,要注意培养学生运用辩证唯物主义的观点去分析问题的能力,使学生对解题的思维过程能够进行有效调控,从而有效提高学生的解题能力.而差异分析是一种典型的探索解题思路的常用方法,所谓差异分析就是对恒等式或不等式等类型的证明题,通过分析题目的条件与结论中所出现的数量特征(如元素的个数、字母系数、指数等)、关系特性(如大于、等于、小于等)及位置特征之间的异同,不断缩小差异来完成解题的一种数学思维方式.
本文以往年高考中一道不等式证明题为例,对使用差异分析进行探索解题思路的过程加以剖析.
题目已知函数f(x)(x∈R)满足下列条件:对任意的实数x1,x2都有λ(x1-x2)2≤(x1-x2)·[f(x1)-f(x2)]和|f(x1)-f(x2)|≤|x1-x2|,其中λ是大于0的常数.设实数a0,a,b满足f(a0)=0和b=a-λf(a).
(1)证明:λ≤1,并且不存在b0≠a0,使得f(b0)=0;
(2)证明:(b-a0)2≤(1-λ2)(a-a0)2;
(3)证明:[f(b)]2≤(1-λ2)[f(a)]2.
分析为了方便起见,不妨把题目的条件分成以下四条:
① 对任意的实数x1,x2都有λ(x1-x2)2≤(x1-x2)[f(x1)-f(x2)],其中λ是大于0的常数;
② |f(x1)-f(x2)|≤|x1-x2|;
③f(a0)=0;
④b=a-λf(a).
(1)首先要证λ≤1,比较目标与条件的差异:条件中含有x1-x2,f(x1)-f(x2)等形式的式子,而求解目标中没有,只含有x,这一差异说明应该把已知条件中x1-x2,f(x1)-f(x2)设法消去,于是从条件①②中找到了内在的联系.若将式②两边同乘|x1-x2|,则得到|x1-x2|·[f(x1)-f(x2)]≤(x1-x2)2,而式①中,由于λ>0, 当x1≠x2时, (x1-x2)2>0,所以λ(x1-x2)2>0,即
(x1-x2)·[f(x1)-f(x2)]>0,
|x1-x2|·[f(x1)-f(x2)]=
(x1-x2)·[f(x1)-f(x2)].
于是得到
(x1-x2)·[f(x1)-f(x2)]≤(x1-x2)2.
因此λ(x1-x2)2≤(x1-x2)[f(x1)-f(x2)]≤(x1-x2)2,而(x1-x2)2>0,所以λ≤1.
第二部分的证明,不妨对命题进行等价转换:不存在b0≠a0,使得f(b0)=0⟺当b0≠a0时f(b0)≠f(a0)=0⟺函数f(x)单调,于是想到函数的单调性,不妨设x1>x2,由前面的分析可知(x1-x2)·[f(x1)-f(x2)]>0,即x1-x2与f(x1)-f(x2)同号,所以函数f(x)在定义域内单调递增,从而问题得到解决.
(2)比较条件和目标的差异,可以发现目标不等式两边的形式在条件中都没有,而不等式左边含b,在条件中含b的只有④,所以先应该考虑缩小差异,从已知条件出发,把左边凑成与目标相同,于是由条件④得
(b-a0)2=[a-a0-λf(a)]2=
(a-a0)2-2λ(a-a0)f(a)+λ2[f(a)]2.
于是问题转化为证明
(a-a0)2-2λ(a-a0)f(a)+λ2[f(a)]2≤
(1-λ2)(a-a0)2=(a-a0)2-λ2(a-a0)2,
即证
λ2[(a-a0)2+f2(a)]≤2λ(a-a0)f(a),
即证λ[(a-a0)2+f2(a)]≤2(a-a0)f(a),由条件①可得
λ(a-a0)2≤(a-a0)[f(a)-f(a0)],
所以λ(a-a0)2+λf2(a)≤(a-a0)[f(a)-f(a0)]+λf2(a),所以只要证
(a-a0)[f(a)-f(a0)]+λf2(a)≤
2(a-a0)f(a)=2(a-a0)[f(a)-f(a0)],
即证λf2(a)≤(a-a0)[f(a)-f(a0)].
而此不等式的右边正是条件① 的右边,故由条件①可知
λ(a-a0)2≤(a-a0)[f(a)-f(a0)],
即只要证λf2(a)≤λ(a-a0)2,由于λ>0,只要证f2(a)≤(a-a0)2,即证[f(a)-f(a0)]2≤(a-a0)2,由条件②知|f(a)-f(a0)|≤|a-a0|,即[f(a)-f(a0)]2≤(a-a0)2,从而解决问题.

[f(b)-f(a)+f(a)]2≤(1-λ2)[f(a)]2⟺
[f(b)-f(a)]2+2f(a)[f(b)-f(a)]+[f(a)]2≤
[f(a)]2-λ2[f(a)]2⟺[f(b)-f(a)]2≤
-2f(a)[f(b)-f(a)]-λ2[f(a)]2.
由条件②知[f(b)-f(a)]2≤(b-a)2,所以只需证
(b-a)2≤-2f(a)[f(b)-f(a)]-λ2[f(a)]2,

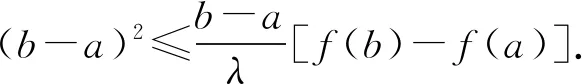

链接练习

2. 设a,b,c均为正数,且a+b+c=1,证明:
3. 已知函数f(x)=ln(2x-1)-m(2x-1)+1的图象在直线y=x的下方.
(1)求实数m的取值范围.
(2)求证:对任意正整数n>1,都有

