对于2020年北京市适应性考试圆锥曲线题的思考

杨雪芹 郑拴平

解析几何是运用代数方法研究几何问题或用几何方法研究代数问题的一门学科．解析几何知识与其他知识联系紧密,综合性强,是选拔人才的必考内容,能重点考查学生知识储备中的基础性、通用性的知识．著名的数学教师孙维刚曾表示学数学应该“八方联系,浑然一体,漫江碧透,鱼翔浅底”． 这是一种体现数学美感的意境,更是彰显学生能力的一个层面．本文对2020年北京市适应性考试圆锥曲线试题进行探究,供读者参考．

1 问题呈现

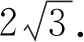
(1)求椭圆C的方程;

2 解法探究

(2)证法1 (直线方程角度代数法)

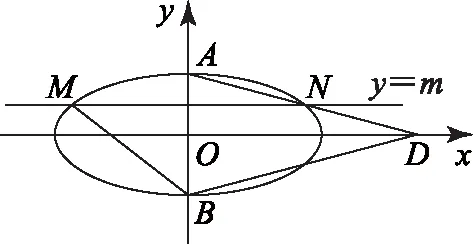
图1

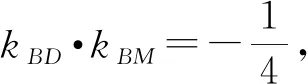
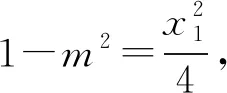
证法2 (点的坐标角度代数法)

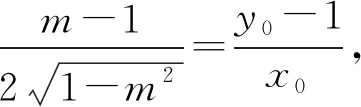
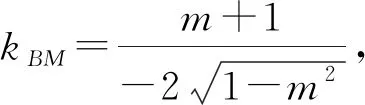
证法3 (参数方程角度换元法)

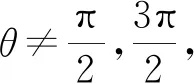
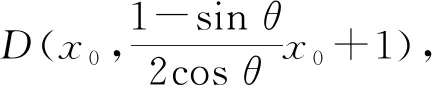
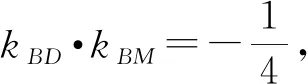
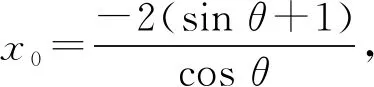
所以点D在x轴上.

证法4 (压缩变形角度几何法)

如图2所示，设直线BD交圆O于点P,连接AM,AP. 在四边形AMBP中,∠MBD=90°,∠AMB=∠APB=90°,所以四边形AMBP是矩形,则BP=AM. 又因为AM=AN,所以BP=AN.

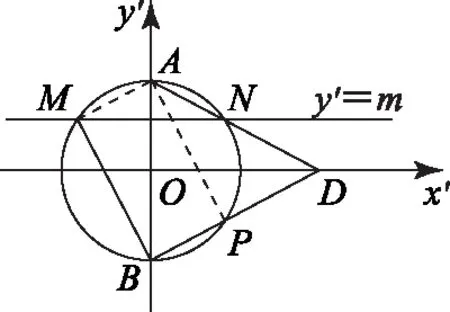
图2

根据相交弦定理得DP·DB=DN·DA,即(DB-BP)·DB=(DA-AN)·DA.所以DB=DA,因此点D在线段AB的垂直平分线上,即点D在x′轴上.所以,在原坐标系下,点D在x轴上.

3 推广与变式

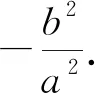
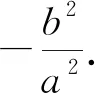
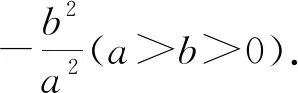
有兴趣的读者可对上述几个变式进行推导,限于篇幅,此处不再赘述．

2020年是北京市新一轮高考改革的起始年,试题既要平稳过渡,又要呈现出“一核四层四翼”的功能．从本文可以看出,试题设计明确、简洁,解答角度灵活,有利于人才的选拔及教学方向的引导,能培养学生提出问题、分析问题、解决问题等能力．