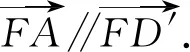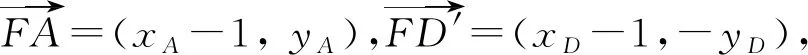平面向量模块的教学要点
2020-06-13陈晓霞
高中数理化 2020年2期
陈晓霞
向量是高中数学的重要考点,纵观近两年高考全国卷,对平面向量的考查除了在客观题中直接考查外,主要体现在将向量作为工具与其他知识进行交会考查.直接考查主要涉及向量的概念、运算等.交会考查主要体现在向量与三角函数、解三角形、解析几何等的交会.
1 把握向量的概念
高考中对向量概念的考查主要涉及向量的模、夹角、共线、垂直等.问题求解中要准确把握相关概念,注意特殊向量、特殊情况.

A. 充分而不必要条件
B. 必要而不充分条件
C. 充分必要条件
D. 既不充分也不必要条件


2 熟练掌握向量的运算
向量的运算包括几何法与代数法两种,几何法主要借助向量加法的平行四边形法则、减法的三角形法则;代数运算是指向量的坐标运算.




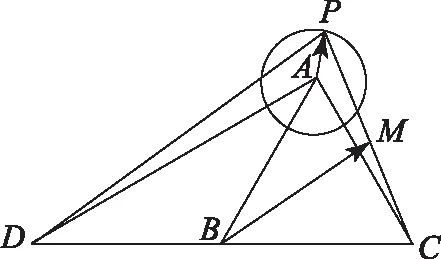
图1

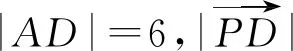
3 处理好向量与三角形的交会
求解平面向量与三角形的综合问题时,要充分利用好向量运算法则以及解三角形的相关定理,仔细观察条件的结构特征,寻找知识间的联系,合理整合相关知识,恰当选择突破口.


由正弦定理得
将两式相加得2R·sin (A+B)=2,2R·sinC=2=c.
方法2 将题目中的两式相加得
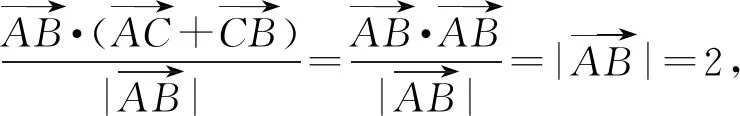
4 明确向量与解析几何的关系
向量与解析几何的交会是高考中的重点考查内容,处理解析几何问题的核心方法是代数法,即将几何问题代数化,而向量的坐标运算就是代数化的有力工具.利用向量可有效处理解析几何问题中的三点共线、平行、垂直、夹角等有关问题.

(1)当l与x轴垂直时,求AM的方程;
(2)设O为坐标原点,证明:∠OMA=∠OMB.

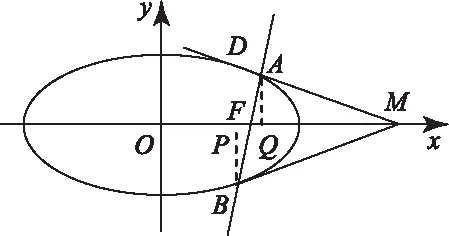
图2
(2)设AM:x=ny+2,与椭圆C联立整理得(2+n2)y2+4ny+2=0,如图2,设AM与C的交点为D,