基于最佳位置点的移动代理路由算法

刘 威，葛 斌，张 岩

(1.安徽理工大学 计算机科学与工程学院，安徽 淮南 232001；2.阜阳师范大学 计算机与信息工程学院，安徽 阜阳 236037)

无线传感器网络(wireless sensor network，WSN)凭借自组织、低成本、长生存周期的特点，而广泛应用于地质勘测、医疗护理等领域。但是由于无线传感器网络节点能量受限且不可补充，使WSN的能量资源有限，无法长时间满足感知数据的收集和处理。因此如何有效利用网络的能量资源是WSN中最具挑战性的问题之一[1]。

1 相关工作

目前基于Client/Server(C/S)模型的路由算法，存在着节点能量消耗不均衡和可扩展性差等弊端[2-4]。移动代理技术广泛应用于完成无线传感器网络中感知数据收集和处理等任务[5]。在设计移动代理模型中，存在的关键问题是移动代理的路径迁徙和网络结构模型的构建。移动代理路线设计可分为单代理和多代理模式。在设计单代理移动路线过程中，移动代理从Sink结点出发完成数据汇聚任务后返回Sink节点。例如局部最近邻优先(local closest first，LCF)[6]和全局最近邻优先(global closest first，GCF)[7]，单个移动代理由于要按照一定的次序访问所有的数据源节点，在小规模网络中能有效的节约能耗，但是不适用于大规模网络结构或复杂网络结构，存在着数据时延和能耗不均衡等问题[8]。在多移动代理迁徙路径规划中，将监测区域内所有传感器节点分成若干个分组，把每一个分组相当于一个单移动代理路线规划进行处理，最后所有的分组内移动代理将所汇聚数据发送给Sink节点。例如GA-MIP（genetic algorithm based multi agent itinerary planning)[9]算法、DSG-MIP(directional source grouping based multi agent itinerary planning)[10]算法、BST(balancing MST-MIP Algorithm)/MST(minimum spanning tree based multi agent itinerary planning)[11]算法等。GA-MIP算法在为移动代理规划路径中主要使用遗传算法来实现，基于GA的算法自适应能力差，不能解决传感器网络动态变化的情况，且需要知道全局信息，不适用大规模网络。BST/MST算法通过考虑总能耗这一主要因素构建出最小生成树[12]，但未能考虑数据源节点的随机分布情况，因此移动代理访问数据源节点的数量波动较大，导致产生局部能量开销大和数据延迟的情况，影响了网络的生存周期。

针对局部移动代理负载不均衡问题，本文首先将网络区域进行六边形划分，选取出移动代理收集数据的最佳位置点(best point,LP)，以移动代理的负载均衡和总能耗为优化目标，提出基于改进粒子群的移动代理路由算法(MABOPSO)，把移动代理访问LP点的顺序看做粒子，经过迭代更新，为移动代理寻找最优路径。

2 问题描述

2.1 MA路径规划问题

假设无线传感器网络由N个同构传感器节点组成，网络中存在一个固定的Sink结点，在监测区域内所产生的数据信息通过M个移动代理的移动传递至Sink节点。移动代理规划目标是最小化移动代理负载的均衡度从而寻找出最优路径。

2.1.1 网络能耗模型

根据文献[13]提出的能耗模型，本文重点考虑通信能耗，并假设忽略其他因素对能耗的影响。即传感器节点的通信能耗ETotal：

其中：ETx(k,d)与ERx(k)分别为节点发送、接收kb数据的所消耗的能耗；εelec为发送1 b数据所需要的能耗；εfs为比例系数；d为矢量距离。

2.1.2 最佳位置点

如图1所示，移动代理位于A、B、C三个不同的位置，设SA，SB和SC表示群组中消耗能量最快的区域，区域由正六边形单元组成，EA，EB和EC表示这些区域消耗的能量。以文献[14]为基础，靠近移动代理的节点需要转发远离移动代理节点的数据而承担更多的任务，这些区域的总数据量表示为∑D(u)，∑D(v)和∑D(w)，ρ为节点分布密度，E0为节点初始能量，Se为六边形的面积，μ为能量节省率。

图1 移动代理位于不同的位置

移动代理处于3个六边形单元的交叉点时，传感器节点不需要接收数据并且仅需要向移动代理发送传感数据。有9个六边形单元可以与移动代理通信，A点的能量节省率为：

移动到交叉点时，B在2个六边形单元中的节点不需要接收数据，B点的能量节省率为：

当移动代理移动到交叉点C时，该六边形单元中的节点不需要接收数据，仅将收集到的数据发送给代理，有6个六边形单元可以直接与移动代理通信，C点的能量节省率为：

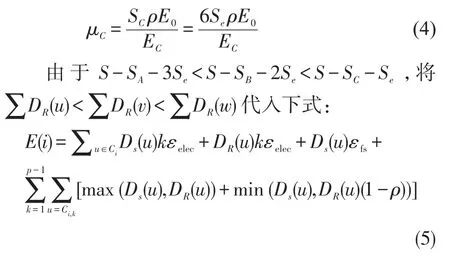
其中：u为六边形单元Ci中的节点；Ds(u)为节点u收集到的数据量；DR(u)为节点u转发的数据量。可得μA＞μB＞μC，因此，当移动代理的位置在点A时，对于平衡所划分六边形能量消耗是最有利的，称点A为最佳位置点。

2.1.3 区域划分

为了确定移动代理收集数据的LP，找寻出最利于均衡网络能耗的移动代理路径，在保证划分的正六边形能够全部覆盖监测区域的情况下，将网络监测区域进行划分，基站计算出正六边形的边长L，结合能耗、网络时延和成本等因素，计算出移动代理收集数据的群组。可以计算出最佳位置点数目与正六边形个数相同，根据文献[15]对最优六边形数目Mopt推导。

其中：EPL、Enon-PL分别表示移动代理在最佳位置点收集数据所消耗的能量和传感器节点与移动代理通信所消耗的能量；M表示正六边形个数；εDA表示融合数据所消耗的能量；DtoMA表示节点到移动代理的距离对ETotal求M的一阶导数并令其为0，可得最优分簇数Mopt。

式（7）最优分簇数只考虑了分簇数对能耗的影响，没有涉及时延。为此，对分簇数进行改进。设新的性能指标参数为Stotol，推导出最优分簇数。

其中:Ttatal表示移动代理在簇内收集数据所花费的时间和通信时延的总和；α为能耗和时间的权重因子；β为时间和成本的权重因子；Ctotal表示移动代理的成本。根据对以上ETotal的推导，可以得出分簇数Mopt与Stotal的关系

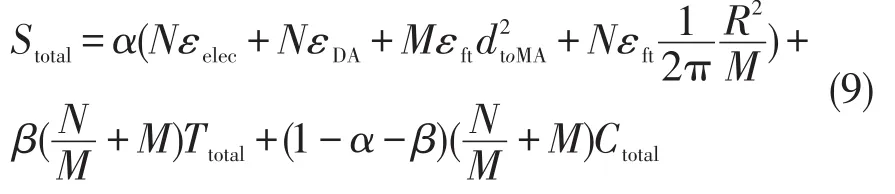
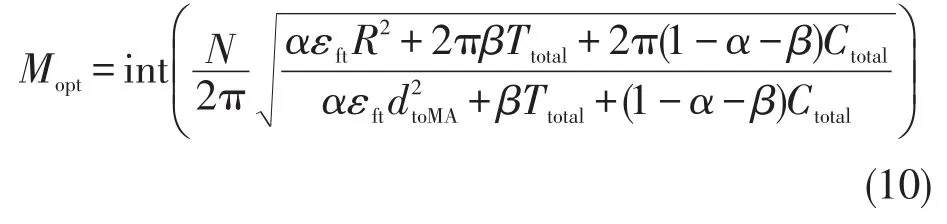
由以上推导可知，当最优分簇数确定后，Stotal可取最小值，此时网络性能指标达到最优。由于式（7）计算出的分簇数是簇内单跳通信最优分簇数，现在将这种簇表示为六边形单元，而式（10）中得到的新最优分簇数（需要对最优分簇数进行取整处理），即可计算出监测区域内由移动代理为簇头簇的个数，在全部覆盖监测区域与最大化节省成本的同时，兼顾通信时延，得出最优分簇数。

2.2 优化粒子群模型的构造

粒子群算法(particleswarm optimization，PSO)是源于鸟群觅食行为活动的智能算法[16-18]，粒子通过学习全局最优解和局部最优解而改变其运动速度和位置，经过若干次的学习最终得到最优解。但由于传统的PSO不能有效的解决离散的优化问题[19]，本文运用MABOPSO算法解决移动代理路径规划问题，其模型简单且能快速收敛。MABOPSO算法使用粒子历史最优解、局部最优解和全局最优解更新其位置和速度，使粒子群具有多样性特点的同时有效地避免早熟现象的出现。

为了均衡移动代理访问群组内所有数据源节点的能耗，本文进行以下均衡度定义：

其中：Ei为节点i的剩余能量；Eave为所有节点的平均剩余能量；Lj为单移动代理j的长度；Lave为所有移动代理的平均长度。均衡度为BA=Eba+λLba，Eba和Lba衡量粒子群在无线传感器网络中性能评价标准，λ为能耗和路径的比例系数，λ=1，依次表示为群组内能量分部程度和群组内移动代理路径迁徙长度。值越小说明均衡度越好[20]。

因此，基于优化粒子群的移动代理路径规划问题可以转化为以下离散多目标问题

其中：Tu表示移动代理收集数据消耗时间；T0表示允许的最大传输时延。

3 算法实现

3.1 粒子群优化模型

本文设计优化粒子群算法MABOPSO，把移动代理访问最佳位置（LP）的不同顺序看做每一个粒子，迭代更新若干轮，以总能耗、移动代理的负载均衡和最大允许的访问时间为目标，对新的移动代理路径进行评价，寻找最优路径。

3.2 算法研究

第k次迭代后所有粒子值的平均值为：

3.2.1 粒子速度和位置更新

粒子的自学习更新速度受粒子群局部最优值和全局最优值的影响，为了便于研究单个粒子的寻优能力和整个粒子群的寻优能力。定义粒子第k次迭代的寻优度为：

Slk反映粒子i在经过k次迭代后的寻优能力参数。Slk＞0时，说明粒子i寻找到更优秀的解；S1k=0时，说明粒子i可能处于停滞的状态。

第k次迭代粒子群局部最优寻优度为：

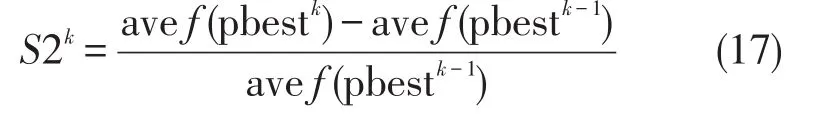
当S2k＞0时，说明粒子找到了更优秀的解；当S2k=0时，说明粒子i可能找到局部最优解或处于停滞的状态。

定义第k次迭代的粒子群全局最优平均值的寻优度为：

当S3k＞0时，说明粒子群找到了更优秀的解；当S3k=0时，算法可能找到了全局最优值或者趋于停滞。定义第k次迭代的学习因子公式为：

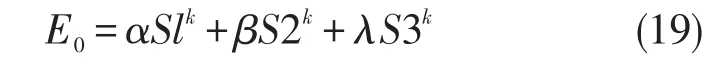
其中，α,β,γ∈[0,1]，且α+β+λ=1。由于学习因子的目标在于寻找出全局最优解，所以λ＞ max(α,β)。

寻优因子是判断当前粒子平均值与全局最优值接近程度的参数，则第k次迭代的寻优因子为：

在粒子群速度公式中，惯性权重影响算法的搜索能力。若惯性权重比较大，则算法拥有强大的全局搜索能力；若惯性权重较小时，算法拥有良好的局部搜索能力。当学习因子较大时，粒子群寻优力度较大，需要降低惯性权重，反之需要增大惯性权重。因此，对惯性权重系数实时调整

其中：w为初始惯性权重；a和b为调节学习E0和pk的系数，0＜a,b＜1，且a+b=1。所以第k+1次时粒子i第d维的改进速度为：

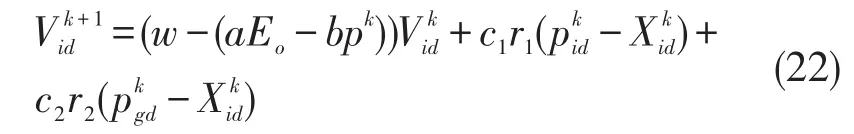
第k+1次粒子i第d维位置为:

3.2.3 更新最优解

适应度函数以网络负载均衡BA和总能耗EI为目标。结合适应度函数值判断当前的粒子的状态，采用公式(22)对粒子历史最优解进行更新，设置迭代更新最优解的次数n，每一轮更新后判断粒子是否满足成为历史最优解的条件，若n次迭代后粒子历史最优解仍未更新，则产生新的粒子。粒子全局最优解取决于粒子历史最优解的更新。设定阈值θ，如果 | pbesti-gbest|＜θ，则pbesti加入全局最优解集合，否则删除粒子。

3.3 算法实施

步骤1：初始化n个粒子，对于粒子向量表示为速度为迭代最大次数为kmax。计算粒子的BA值、EI值、局部最优值及全局最优值；

步骤2：初始化迭代次数k=1；

步骤3：根据公式(23)更新粒子i的位置

步骤4：对粒子i函数值进行更新，并更新出局部最优函数值和全局最优函数值，并计算出下一轮的改进权重系数，对下一轮粒子的迭代速度进行更新；

步骤5:对迭代次数进行判断，判断是否等于kmax，若不等于，则k=k+1，返回步骤3，若等于kmax，则输出全局最优函数值集合，结束算法。

4 仿真实验与结果分析

为证明本文所提出的基于优化粒子群算法MABOPSO的有效性，选取LCF算法、GCF算法和GA-MIP算法，主要通过总能量消耗、任务延迟、移动代理路径均衡度三个方面对比这四类算法的性能。

4.1 实验环境设置

本文使用Matlab R2016a平台做仿真实验，实验参数见表1。

表1 仿真实验参数

4.2 实验结果分析

数据源节点数，设置为5～40，仿真中设置100个随机数种子，在总能量消耗方面(取平均值)对四类算法进行比较，如图2。当数据源节点数较少时，MABOPSO算法、LCF算法、GCF算法和GAMIP算法在总能量消耗方面大致相同，随着数据源节点数的增加，LCF算法明显存在着优势，由于多移动代理算法需要多个移动代理协作完成感知数据的汇聚，每个移动代理在进行数据汇聚时增加了额外的能耗开销。在路径选择中充分考虑了移动代理负载均衡，因此总能耗低于同类算法。

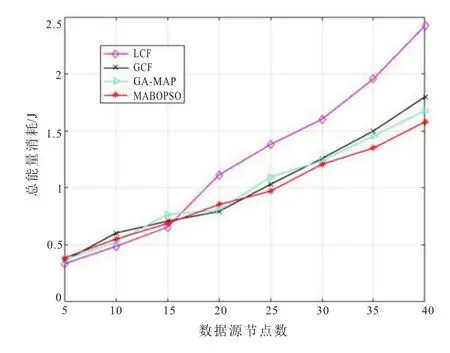
图2 数据源节点数对总能量消耗的影响

图3为数据源节点数量与任务延迟之间的关系，随着访问数据源节点数目的增加，数据延迟整体将呈现上升的趋势。LCF算法在任务延迟方面性能远低于多移动代理算法，单移动代理随着数据源节点数增加而出现较大延迟，而多个MA以协作的方式同时访问分布在网络区域的数据源节点，将会有效的降低任务延迟。因为单个代理访问节点增加，所以GA-MIP、GCF任务延迟有所增加。而MABOPSO算法由于是在网络区域划分后选取最佳位置点的基础上进行移动代理路径规划，因此能有效的减小延迟。

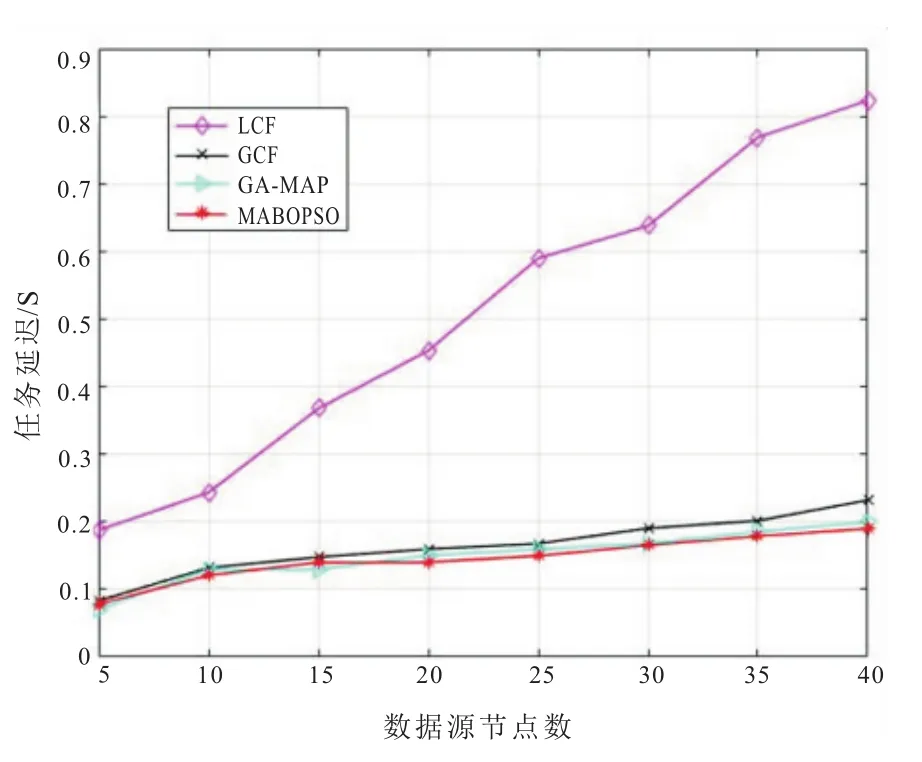
图3 数据源节点数对任务延迟的影响

移动代理均衡度有效衡量了移动代理路径规划算法的性能，图4中LCF算法均衡度明显低于其他3种算法，而 GA-MIP、GCF和MABOPSO算法在数据源节点较少时性能相似，随数据源节点数的增加，MABOPSO算法的均衡度优于GAMIP、GCF，充分说明MABOPSO算法的有效性。

图4 数据源节点数对移动代理均衡度的影响

5 小结

本文通过对网络通信区域的划分，引入最佳位置点让移动代理汇聚数据更加高效，并以粒子群算法为基础对其进行优化，结合学习因子和寻优因子改进速度公式的权重因子，计算每一个粒子的BA值和能耗EI，迭代更新找出移动代理的最优移动路线。在不同数据源节点的条件下，依次与LCG、GCF和GA-MIP算法进行总能量消耗、任务延迟和移动代理均衡度等方面的比较。实验结果表明本算法在考虑移动代理负载均衡的无线传感器网络中能够有效优化移动代理路径且有效减少网络能耗，相比于同类算法更好的实现了负载均衡，从而延长网络生存周期。