考虑自动化/人工混合站位的装配系统瞬态产能计算方法

侯宇戡，李 原，张 杰，姜寿山

(西北工业大学 机电学院，陕西 西安 710072)

0 引言

智能决策是构建智能车间的关键要素之一，而准确掌握系统实时运行状态是影响智能决策制定的先决条件[1-2]。在航空航天复杂零部件产品装配环节中，装配系统具有自动化/人工站位混合程度高[3]、待装配零件/工具选择种类多[4]、缓冲区容量设置灵活性高[5]等特点，从而使系统的实时产能变化呈现出较强的耦合性与非线性，成为制约系统智能决策制定的瓶颈。因此，有必要针对自动化/人工站位混合的装配系统开展系统实时产能建模分析，以提升智能制造体系下系统状态的感知能力，并为航空航天类复杂零部件产品生产系统中智能化精准决策的实现奠定基础[6]。

制造系统瞬态性能的提出是为了描述任意时刻系统运行的性能，相对于保持不变的稳态性能，其能够真实反映系统性能随时间的动态变化[7]。数十年来，针对离散生产系统建模问题，国内外学者们开展了大量研究，然而大多数研究方法均针对系统稳态性能开展[8-9]。例如，最早的装配系统建模研究主要基于排队模型，对简单的三站位结构装配系统进行了有效分析[10]；随后Petri网也被用于解决装配系统的建模与分析问题[11]。因为系统运行中各工作站位的随机故障与各缓冲区的容量限制互相影响，会加剧生产节拍的波动，所以针对具有不可靠设备及有限容量缓冲区的装配系统建模问题最为复杂且更符合工程实际需求。Gershwin[12]提出一种基于分解与合并的方法，可以有效地对几何分布型工作设备可靠性模型和具有有限容量缓冲区的装配系统进行稳态性能分析；Chiang等[13]研究了具有伯努利型工作设备和有限容量缓冲区装配系统的稳态性能评估问题。相对于比较成熟的制造系统稳态性能研究，有关系统瞬态性能的建模和分析方法仍比较少，现有研究主要围绕串行制造系统提出。例如，Meerkov等[14]研究了两站位生产系统的瞬态性能问题；Wang等[15]研究了生产系统具有多个站位及有限容量缓冲区的情况；Ge等[16]对具有返工回路的串行制造系统的瞬态性能进行了分析；而有关不可靠工作设备和有限容量缓冲区的装配系统瞬态性能分析问题仍亟待解决。

在自动化/人工两类站位混合并存的装配系统中，自动化站位指不需操作人员干预的自动化程度较高的加工站位，人工站位指工艺过程需要操作人员参与的自动化程度较低的站位。自动化站位的可靠性在工艺装备制造完成后已确定，而且在正常使用过程中波动较小，一般通过加工成品率来度量；对于人工站位而言，由于待装配零件/工具的选择种类较多，操作人员在对象和工具选择中的人为操作失误是影响站位可靠性最主要的因素[17]。从信息论的角度来看，待装配零件/工具的种类数量越高，装配选择过程的不确定性就越大，而理解它所需要的信息量就越多。例如，Zhu等[18]基于信息熵提出操作人员选择复杂性(Operator Choice Complexity, OCC)，用以对选择过程中的平均不确定性和随机性进行度量，研究表明装配选择种类的信息熵与其有序程度成反比；Liu[19]发现了操作人员的平均反应时间与选择对象的对数函数之间存在线性关系。类似地，人因可靠性分析方法也是研究人行为理论和失误的研究方法，经典的研究模型主要有失误预测技术(Technique for Error Rate Prediction, THERP)、成功似然指数法(Success Likelihood Index Methodology, SLIM)、认知可靠性模型(Human Cognitive Reliability, HCR)等，其中HCR模型提供了一种基于实验数据的精确模拟方法，能够较为客观地对人因失误的机理进行研究。例如，Yang等[20]基于HCR方法研究了操作人员在进行选择过程中的可靠性模型，具体表达为以平均反应时间为自变量的威布尔分布函数或对数正态分布函数。基于Liu[19]和Yang等[20]的研究成果，本文将对装配系统中人工站位的可靠性模型进行表征，以为系统瞬态性能计算提供有效的支持。

本文在考虑自动化/人工站位混合、待装配零件/工具选择多样性、有限容量缓冲区的基础上，提出一种装配系统瞬态产能计算的新方法。本文的研究重点是解析装配系统中各类变量间的耦合作用关系，并对系统的非线性瞬态产能进行有效预测，因此假设所研究的装配系统各站位具有相同的加工速率，以降低建模过程的复杂性。

1 问题描述及建模假设

典型的装配系统结构如图1所示，其中mi,j表示工作站位，bi,j表示站位间的缓冲区(i=1,2，j=1,2,…,Ni)；生产线(m1,1,m1,2,…,m1,N1)和(m2,1,m2,2,…,m2,N2)是为最终产品提供零件供应的两条分支生产线，两种零件将在主生产线(m3,1,m3,2,…,m3,N3)上进行组装和后续加工；N1,N2,N3表示每条生产线所包含的工作站位的个数(N1≥1，N2≥1，N3≥1)。假设mi,j在任意时刻处于非故障的概率为Pi,j，相应地，mi,j在任意时刻处于故障的概率为1-Pi,j。由于各站位处于非故障或故障属于站位本身的失效状态且不受其他站位的影响，每个站位在任意时刻处于何种状态为相互独立事件。假设mi,j上的工具种类数量为Ti,j，待装配零件种类数量为Ai,j，bi,j的最大库存量为Qi,j。基于混合站位的装配系统瞬态产能模型将基于图1所示的系统结构建立，前文已经假设该装配系统各工作站位在单位时间内可处理相同个数的零件，为降低计算复杂度，进一步假设其数量为1。与此同时，将生产计划总时间按照各站位相同的加工时间均匀且离散地分成若干时间段，假设离散时间段的总数为M，则初始时刻表示为t=0，第一个时刻结束表示为t=1，最后时刻表示为t=M。

为了对装配系统进行瞬态产能建模，还需采用一些离散生产系统建模的基本假设：①两条装配支线上的第一台工作站位永远不会处于饥饿状态(原料充足)，主生产线上的最后一台工作站位永远不会处于阻塞状态(订单不断)；②工作站位所处的状态在每个时间段的开始确定，缓冲区的状态在每个时间段的末尾确定；③生产过程满足“时间相关故障”和“加工前阻塞”的假设[9]。

2 装配系统瞬态跃迁模型

2.1 混合站位可靠性模型

自动化站位的可靠性在工艺装备确定时已经基本确定，而且在正常生产中波动较小，成品率是其可靠性特征的重要指标，因此可以使用产品的成品率度量此类站位的可靠性。对于需要操作人员支持的人工装配站位，由于工具种类多、零件数量大，操作人员需要从一定数量的工具和零件中挑选出正确的对象来完成工艺操作，因此其站位可靠性由操作人员的选择可靠性和工艺可靠性共同决定。根据OCC的定义[18]，mi,j的操作人员对Ti,j和Ai,j的OCC可以表示为信息熵的形式：

(1)

(2)

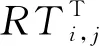
(3)

在式(3)的基础上，根据Yang等[20]的研究，人工站位mi,j的可靠性计算公式为

Pi,j=ωi,j·e-[RTi,j/ηi,j]γ。

(4)

式中：ωi,j为mi,j上的工艺可靠性；ηi,j为威布尔可靠性函数的比例参数；γ(γ>1)为威布尔可靠性函数的风险率。从式(4)可以看出：①当人工站位装配操作过程的OCC为0时，其站位可靠性只取决于ωi,j；②当Ti,j或Ai,j的数量增多，即OCC增大时，人工站位的可靠性降低。

2.2 系统瞬态跃迁描述模型

为了在装配系统中公式化描述生产运行规则，引入如下算子和符号来描述某些特定对象或者特定事件的发生：

(1)采用算子P描述事件E发生的概率，即P[E]。

(2)采用算子Ф描述对象O在时刻t处于状态S的事件，即Ф(O,S,t)。

(3)采用算子H描述多个对象(O1，O2，O3，…)在时刻t分别处于状态(S1，S2，S3，…)的事件，即H(O1,O2,O3,…/S1,S2,S3,…,t)。

因此，可以得到如下推导：

P[H(b1,b2,b3/k1,k2,k3,t)]

(5)

(4)采用算子T描述特定对象O在时间t内从状态S1转变到S2的概率，即TS2,S1(t)。

(5)采用以下符号描述某特定工作站位在单位时间内所处的不同状态：

Up表示站位在单位时间段内处于非故障的运行状态；

Dn表示站位在单位时间段内处于故障的停机状态；

Pr表示站位在单位时间段内处于生产的状态；

nPr表示站位在单位时间段内处于不生产的状态；

St表示站位在单位时间段内处于饥饿的状态；

nSt表示站位在单位时间段内处于不饥饿的状态；

Bl表示站位在单位时间段内处于阻塞的状态；

nBl表示站位在单位时间段内处于不阻塞的状态；

Id表示站位在单位时间段内处于空闲的状态；

θ表示站位所有可能发生状态的全集。

基于上述定义的站位状态表示方法，系统中工作站位各状态之间的逻辑关系如图2所示。在系统运行中，各站位在任意时间都有不同的运行状态(如生产、饥饿、阻塞等)，一般每个站位在任意时间段内只能处于一种特定的状态，除非该状态可以与其他状态同时发生，例如饥饿与阻塞可以同时发生。在图2所示站位状态关系的基础上，采用算子Ф可得：

Φ(mi,j,Pr,t)=Φ(mi,j,Up,t)∩

Φ(mi,j,nSt,t)∩Φ(mi,j,nBl,t)；

Φ(mi,j,nPr,t)=Φ(mi,j,Dn,t)∪

Φ(mi,j,St,t)∪Φ(mi,j,Bl,t)；

Φ(mi,j,Up,t)∪Φ(mi,j,Dn,t)=θ；

Φ(mi,j,Up,t)∩Φ(mi,j,Dn,t)=∅；

Φ(mi,j,Pr,t)∩Φ(mi,j,St,t)=∅；

Φ(mi,j,Pr,t)∩Φ(mi,j,Bl,t)=∅。

(6)

因为各工作站位具有无记忆性，所以采用缓冲区的即时占用量描述系统的瞬时状态。系统瞬时状态变化的根本原因是各站位在生产过程中随机地呈现出不同的运行状态。为了对该过程进行说明，以图3所示的三站位装配系统(N1=N2=N3=1)为例，假设三元数组(αβγ)表示缓冲区b1，b2，b3的即时占用量(α,β,γ∈N，α≤Q1，β≤Q2，γ≤Q3)。通常情况下，装配系统在开始生产时各缓冲区的占用量均为0，因此(000)表示t=0时刻系统所处的状态。随着时间的推移，系统内缓冲区占用量的变化会根据站位处于非故障或故障状态而发生相应的变化，假设“×”表示工作站位在单位时间内处于故障的停机状态，“√”表示工作站位在单位时间内处于非故障运行状态，则图3所示装配系统的站位组合状态可以定义为8种不同类型，如表1所示。在不同类型的站位组合状态的影响下，缓冲区的瞬时状态将进行规律性地跃迁，如图3所示。例如，假设系统在t=0时刻的状态为(000)，而且站位组合状态为表1中的A(或者B)类型，则系统在t=1时刻的瞬时状态仍为(000)。由此可见，在8种不同类型的站位组合状态作用下，系统在t=1时刻只能处于(000)(100)(110)(010)4种状态中的某一种。类似地，若系统在t=1时刻的状态为(100)，则在t=2时刻系统只可能处于(100)(110)(200)(210)4种状态中的某一种。基于算子P和算子H，上述系统瞬态的跃迁关系可表示为

P[H(b1,b2,b3/k1,k2,k3,t)]

(7)

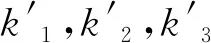
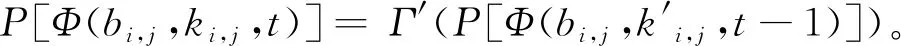
(8)

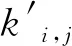
表1 三站位装配系统站位组合状态集

2.3 系统瞬态映射关系解析

基于图4所示的瞬态转移关系，根据全概率公式可得：

P[Φ(bi,j,2,t-1)]；

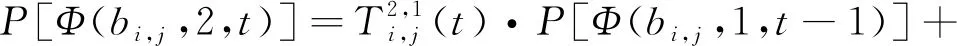
P[Φ(bi,j,3,t-1)]；

…

P[Φ(bi,j,k+1,t-1)]，0≤k≤Qi,j-1；

…

P[Φ(bi,j,Qi,j-2,t-1)]，0≤k≤Qi,j-1；

P[Φ(bi,j,Qi,j,t-1)]。

(9)

式(9)中所有的状态概率满足

(10)

式(9)也可以改写为如下矩阵运算的形式：

(11)

可见，式(11)所描述的函数关系即为式(8)中的映射函数Γ′()。

2.4 站位瞬态行为逆向建模

系统瞬时状态变化的根本原因是各站位在生产过程中呈现出不同的运行状态，因此可以基于这种关系对站位的瞬态行为进行逆向建模，以实现对转移概率的求解。实际上，装配系统内每个缓冲区即时占用量的变化均与其上下游工作站位状态的变化严格对应。例如，当bi,j的即时占用量在时刻t-1为k且在时刻t为k+1时，在时刻t-1～t的单位时间内mi,j一定处于Pr状态，且mi,j+1一定处于nPr状态；类似地，当bi,j的即时占用量在时刻t-1为k+1且在时刻t为k时，在时刻t-1～t的单位时间内mi,j一定处于nPr状态，且mi,j+1一定处于Pr状态；当bi,j的即时占用量在时刻t-1和时刻t均为k时，在时刻t-1～t的单位时间内mi,j和mi,j+1一定同时处于Pr或nPr状态。

=P[Φ(mi,j,pr,t)∩Φ(mi,j+1,npr,t)|

Φ(bi,j,k,t-1)]。

(12)

(1)当k=0时，由于Φ(bi,j,0,t-1)]⊆Φ(mi,j+1,npr,t)，可得

P[Φ(mi,j+1,npr,t)|Φ(bi,j,k,t-1)]=0；

(13)

因此

(14)

根据式(6)可得

nSt,t)∩Φ(mi,j,nBl,t)|Φ(bi,j,k,t-1)]；

(15)

由于Φ(bi,j,k,t-1)]⊆Φ(mi,j,nBl,t)，可得P[Φ(mi,j,nBl,t)|Φ(bi,j,k,t-1)]=1。因此，可以进行如下推导：

Φ(bi,j,k,t-1)]=Pi,j-P[Φ(mi,j,St,t)]。

(16)

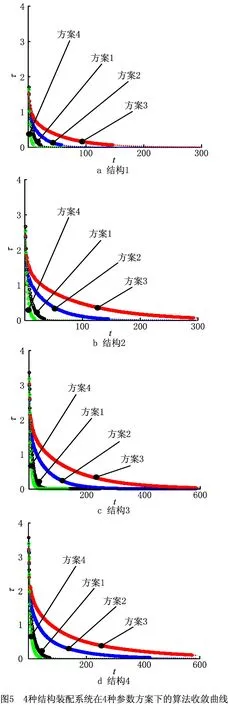
(2)当0

Φ(mi,j,nBl,t)∩(Φ(mi,j+1,Dn,t)∪

Φ(mi,j+1,St,t)∪Φ(mi,j+1,Bl,t))|

Φ(bi,j,k,t-1)]；

(17)

因为Φ(bi,j,k,t-1)]⊆Φ(mi,j,nBl,t)，可得P[Φ(mi,j,nBl,t)|Φ(bi,j,k,t-1)]=1，而且存在

P[Φ(mi,j+1,St,t)|Φ(bi,j,k,t-1)]=0，

(18)

所以可得

(Φ(mi,j+1,Dn,t)∪Φ(mi,j+1,Bl,t))|

Φ(bi,j,k,t-1)]；

(19)

根据式(6)可得

(1-Pi,j+1+P[Φ(mi,j+1,Bl,t)])。

(20)

综上，

(21)

(22)

(23)

3 装配系统瞬态模型的求解

若某站位在单位时间内处于饥饿状态，则表示虽然该站位处于非故障状态，但是由于其上游缓冲区在此时刻的即时占用量为零，导致该站位因原材料缺失而无法正常完成生产任务。因此，mi,j在时刻t处于St状态的概率为

P[Φ(mi,j,St,t)]=

(24)

若某站位在单位时间内处于阻塞状态，则表示虽然该站位处于非故障状态，但是由于其下游缓冲区在此时刻的即时占用量达到上限，而且下一个工作站位在单位时间内也无法立即接收零件以减小上游缓冲区的库存占用量，导致该站位因零件加工后无法移出而产生空闲。因此，mi,j在时刻t处于Bl状态的概率为

P[Φ(mi,j,Bl,t)]=

(25)

基于图2所示的工作站位状态关系，推导出mi,j在时刻t的瞬态生产率为

P[Φ(mi,j,Pr,t)]=P[Φ(mi,j,

Up,t)∩Φ(mi,j,nSt,t)∩Φ(mi,j,nBl,t)]

=Pi,j-P[Φ(mi,j,St,t)]-P[Φ(mi,j,

Bl,t)]+P[Φ(mi,j,St,t)∩Φ(mi,j,Bl,t)]。

(26)

装配系统瞬时状态的跃迁可以通过系统缓冲区即时占用量的变化进行描述，因此系统前后时刻瞬态的映射关系可以用缓冲区即时占用量的转移矩阵表征。通过有效解析装配系统的实际运行规则，可以实现站位瞬态行为的逆向建模，从而求解各缓冲区的转移概率。基于上述分析，将式(21)～式(25)带入式(11)，可见系统在时刻t的瞬时状态只与时刻t-1的瞬时状态相关，这与式(8)得到的结论完全相同。因此，一旦给定系统在t=0时刻的缓冲区即时占用量和系统参数设置，就可以通过式(11)计算t=1时刻的缓冲区水平，重复该步骤，则可递推式确定系统在以后任意时刻的瞬时状态。实质上，以递推式方法不断计算缓冲区即时占用量的过程正是通过系统建模的方式模拟系统的真实运行过程。在获取系统任意时刻的瞬态信息后，装配系统的瞬态生产率可采用式(26)计算。

4 实例分析

为了说明本文所提方法的有效性，采用不同结构的装配系统以及不同系统参数的设置方案开展实例分析。在图1所示的装配系统中，通过设置不同的N1，N2，N3来设计不同的系统结构，如表2所示。假设已经基于生产数据计算出装配系统各站位的可靠性数值，在此基础上设计了4种方案的系统参数设置，如表3所示。

表2 装配系统的4种结构

表3 装配系统参数设置的4种方案

假设4种结构的装配系统在时刻t的缓冲区状态均为S(t)，有

Si(t)=

(27)

式中Si(t)表示bi在时刻t的瞬时状态(i=1,2,…,v;v=N1+N2+N3-1)。在系统运行的初始时刻，即t=0时刻，系统中各缓冲区的即时占用量均为零。针对4种结构的装配系统，在4种参数设置方案下使用本文所提计算方法，当满足迭代运算的收敛条件‖S(t+1)-S(t)‖≤10-5时，系统最终达到稳态，记为S(d)。因为τ=‖S(t+1)-S(d)‖可被用于描述系统在运行过程中达到稳态的收敛速率，所以绘制4种结构装配系统在4种参数方案下τ的变化曲线，以对本文所提方法的收敛性进行说明，如图5所示。

从图5可见，对于4种结构装配系统与4种参数设置方案组成的所有案例，本文所提方法均能快速收敛，即系统运行可以达到稳态。同时，若系统内各站位的可靠性数值相同，则缓冲区的最大库存量越小，系统到达稳态的速度越快；若缓冲区的最大库存量相同，则站位可靠性数值越小，系统到达稳态的速度越快。

以结构4的装配系统为例，采用本文方法计算4种参数设置方案下的系统瞬态生产率，记为案例1～案例4，其生产率曲线如图6所示；同时，在Em_plant仿真软件平台上对以上4种案例进行仿真模拟，其仿真运算结果分别绘制于图6a～图6d中，以对本文所提方法的有效性进行说明。

从图6可见，对于以上4种案例，本文方法所计算的装配系统瞬态生产率均较好。同时，在4种案例中，本文方法的计算结果均能获得与仿真模拟运算、经典稳态性能分析方法[9]的计算结果相同的稳态值，说明本文方法在求解系统稳态产能方面是有效的。

为了验证本文方法的适用性，针对结构4的装配系统应用本文方法计算了多种参数设置下的稳态生产率。具体地，假设所有站位具有相同的可靠性数值R，同时R以步长0.05从0.60均匀地变化到0.99；所有缓冲区具有相同的最大库存水平Q，同时Q从1均匀地增加到10。对所有参数设置情况应用本文方法、仿真模拟和经典稳态性能计算方法[9]，所得的系统稳态生产率(PR)如图7和图8所示。

从图7可见，对于任意参数设置下的结构4装配系统，本文方法均能获得与经典稳态方法相同的计算结果；从图8可见，本文方法的计算误差会随Q的减小而增大，然而即使在Q=1时计算误差达到最大的情况下，其误差也仍小于3%，说明了本文方法的适用性。

5 结束语

本文针对自动化/人工两类站位混合并存的装配系统，在考虑待装配零件/工具选择多样性、缓冲区容量设置灵活性等特点的基础上，提出一种装配系统瞬态产能的计算方法。该方法基于信息熵理论和认知可靠性模型构建了站位可靠性模型；通过构造工作站位与缓冲区的瞬时状态集实现了系统运行中站位瞬态行为的逆向建模；推导了系统瞬态映射关系矩阵并采用递推法对瞬态产能进行求解。研究成果有助于提升智能制造体系下系统状态的感知能力，奠定航空航天类复杂零部件产品生产中智能决策的实现基础，下一步研究工作将围绕智能车间中精准决策的制定展开。