百叶轮抛光TC4的接触弧长试验研究

鲜 超，史耀耀，蔺小军，刘 德

(西北工业大学 现代设计与集成制造技术教育部重点实验室，陕西 西安 710072)

0 引言

在抛光、磨削等加工过程中，磨具与工件动态接触区的几何特征、热力特性等性质对加工质量有重要影响，接触弧长则是其中非常重要的几何特征。抛光(磨削)接触弧面定义为：在一定的磨削深度下，砂轮的理想外圆表面与工件在磨削区内重合部分的曲面。抛光(磨削)接触弧长定义为：与砂轮轴相垂直的平面和几何磨削接触弧面相交而形成的曲线[1]。

接触弧长与抛光(磨削)力、抛光(磨削)温度，以及磨具和工件变形、加工精度都具有关联性，因此研究抛光(磨削)过程的接触弧长具有重要的意义。

国内外专家学者对接触弧长的研究已超过数十年，取得了很多理论成果。Lindsay等[2]认为磨粒为一个个弹性变形体，忽略磨削深度的影响，建立了接触弧长的理论计算公式；Brown等[3]同时考虑磨粒、工件和砂轮的变形，忽略磨削深度的影响，也建立了接触弧长的理论计算公式；Kumar等[4]、Tsuwa[5]、Vansevenan[6]和VerkerkIs[7]假设工件与砂轮在磨削时均为弹性光滑体接触，分别建立了接触弧长的理论计算公式；Maris[8]建立了接触弧长的经验公式；Brandin[9]认为表面粗糙度会对磨削深度产生重要影响，建立了与粗糙度相关的接触弧长的理论计算公式；Qi等[10]综合考虑磨粒、磨具和工件的变形以及粗糙度对接触弧长的影响，给出了接触弧长的理论计算公式。

关于接触弧长的实际测量方法，相关专家学者经过几十年探究，已经给出了多种测量方法，根据测量状态的不同，这些测量方法大体分为静态测量法和动态测量法两类。静态测量方法是在磨削进行过程中突然停止磨削，通过测量并观测工件表面的磨削痕迹获得接触弧长等信息，Brown等[11]采用爆炸式快停装置对平面磨削的接触弧长进行了研究，发现实际接触弧长约为几何接触弧长的1.5倍；Gu等[12]提出双半沟槽技术来测量磨削接触弧长，具体原理为在砂轮圆弧面上刻两条沟槽，沟槽处不参与磨削，磨削时在工件已磨表面会周期性地产生一系列等距凸台，在凸台两端会留下对应沟槽两端磨粒的划痕，测量这些划痕的长度可得接触弧长。动态测量法[13]是基于热电偶技术的测量方法，其通过磨削过程中每一个磨粒都会产生一个峰值电信号来获得磨具热电偶的接触时间，接触长度则根据进给运动过程中热电偶与磨具表面从开始接触到接触结束，工件表面上的热结点所运行的距离来确定，有效磨粒接触长度等于磨具和热电偶的接触时间与工件速度的乘积，然而使用该方法获得的信号有时不稳定。

毛聪[1]、周德旺[14]研究了不同的工艺参数(磨削深度、磨具转速、工件进给速度)、磨具参数(磨具直径、材料、粒度)、工件材料、磨削方式对实际接触弧长的影响，以及磨削温度、磨削力和接触弧长的关系，发现磨削温度、磨削力和接触弧长正相关，磨削力增大和磨削温度升高均会增大接触弧长，接触弧长增大也会导致磨削温度升高。

传统磨削的磨具刚度大，磨削力大，磨削接触区温度高，文献[15-23]针对抛光航空发动机整体叶盘提出一种利用百叶轮进行抛光的方法，该磨具具有一定的柔性，可以避免叶盘欠抛或过抛；本文通过试验数据对百叶轮抛光TC4试块过程的接触弧长进行了计算，研究了接触弧长和工艺参数之间的定量和定性关系，以及接触弧长和表面质量之间的定性关系，通过接触弧长将工艺参数和表面质量联系起来，并以表面质量为目标函数进行了工艺参数优化。

1 百叶轮柔性抛光原理

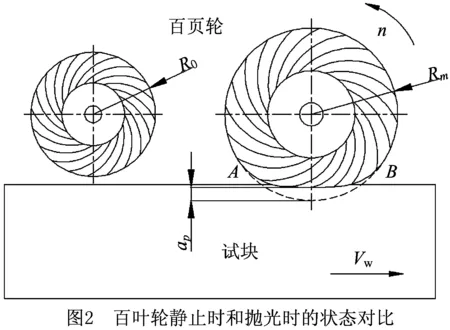
图1所示为百叶轮实物图，图2所示为百叶轮静止和旋转时的半径变化示意图，图中左侧为静止时的百叶轮，其半径为R0，右侧为以一定转速旋转并做抛光试块时的百叶轮，随着高速旋转，每片砂带叶会因离心力而沿径向展开，半径随之增大到Rm，百叶轮半径的增大量为Δr=Rm-R0，使其由近刚性磨具变为柔性磨具。百叶轮的压缩量用ap表示,当ap≤Δr时，为柔性抛光，此时实际抛光的切入深度非常小，如图2所示；当ap>Δr时，为刚性抛光。百叶轮半径随转速的变化规律如图3所示[19]。

2 试验装置和试验方案

2.1 试验设备和材料

试验使用的机床为本实验室自行研发的五轴联动数控抛光机床，该机床专门对整体叶盘进行抛光，鉴于整体叶盘叶片为自由曲面，叶盘中间端面为平面，设计机床五轴联动运动形式，五轴包括X，Y，Z3个直线运动轴，以及磨具旋转主轴绕X轴旋转的U轴和工作台绕Z轴的旋转轴V轴，整体叶盘的叶片具有薄壁、动态刚度差等特性，由于抛光机理较为复杂，本文不予研究，只研究整体叶盘表面曲率较小和近似于平面的部位进行抛光试验。抛光磨具采用粒度分别为120#，180#，320#，直径为17 mm、宽为14 mm的百叶轮，百叶轮由砂布层叠和树脂胶粘而成，其砂布的磨粒为棕刚玉，主要成分为氧化铝；试块选择TC4材料，试块的尺寸为50 mm×30 mm×10 mm的钛合金。TC4在高温下的抗变形能力强、比强度高、抗腐蚀性强，综合机械性能良好，广泛应用于航空航天等领域，尤其是航空发动机制造领域。为改善叶盘表面质量、提高使用寿命，航空发动机整体叶盘铣削后要进行表面抛光，本文试验即基于该背景，因此工件材料选择具有代表性的钛合金TC4。

2.2 试验原理和步骤

试验系统原理如图4所示，抛光力通过试块传给kistler 9257B型三向测力仪，测力仪将力信号转换为电压信号，经过放大器、数据采集仪输入计算机，计算机可以采集X，Y，Z3个坐标轴方向力随时间的变化信号；抛光温度信号采用德国InfraTec/VH-480型红外热成像检测系统采集，采集的红外图像可直接输入计算机。

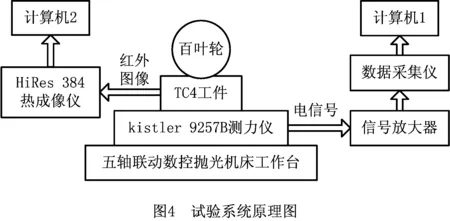
试验具体步骤为：①按照图4所示原理图装夹好测力仪和工件，连接好采集设备；②选定主轴转速使主轴旋转，此时百叶轮叶片甩开，进行对刀，使甩开的百叶轮最下沿母线与待抛光试块表面刚好接触；③在抛光程序中设置压缩量、与对刀时相同的主轴转速，以及其余参数；④运行抛光程序，在百叶轮接触试块之前在计算机上同时点击测力和测温软件的开始采集按钮，百叶轮离开试块后关闭按钮，将抛光力信号和热成像图像完整地采集到计算机。试验的力和温度采集现场如图5所示，图中左侧计算机采集的为热成像图片，右侧计算机采集的为抛光力信号，其中由上到下依次为X，Y，Z轴抛光力信号。

接触弧长的影响因素多，影响机理复杂，本文只考虑对其影响较为明显的主轴转速、压缩量、进给速度，以及百叶轮的粒度、直径和磨损量这几个工艺参数。百叶轮的磨损量很难测量和定量描述，本文未研究其对接触弧长的影响规律；因为整体叶盘通道狭窄，还要兼顾在叶盘曲率较大处附近欠抛或过抛，所以百叶轮直径只能选取较小的值，为了避免抛光通道和叶盘其余表面时更换不同直径的百叶轮，百叶轮直径一般选取8，10，12，14，17等值，百叶轮直径一旦选好，就不能更改。因此，本文主要探寻主轴转速、压缩量、进给速度、百叶轮粒度对接触弧长的影响，保持其余影响因素为常量。

本试验所采用的机床设计最高主轴转速为10 000 r/min，为了使试验过程包含的主轴转速范围较大，使抛光效率不至于太低，选择主轴转速n在4 000 r/min～8 000 r/min之间；根据图3可知百叶轮旋转时的半径增大量在1 mm～1.62 mm之间，压缩量太小则抛光效率太低，压缩量太大则抛光过程会变为刚性抛光，根据经验，压缩量ap的选取范围在0.5 mm～1.5 mm之间；为了保证能测得较稳定的抛光力信号，同时为了提高抛光效果、避免抛光效率太低，进给速度f的选取范围在100 r/min～300 r/min之间；为了兼顾抛光效率和抛光后的表面质量，百叶轮粒度Pm的选取范围在120#～320#之间。本试验选取的4个因素的水平分布如表1所示。

表1 试验因素及水平分布

为了建立接触弧长和试验因素之间的定量关系，本试验使用响应面分析法，其中中心复合设计方法的工艺参数如表2所示。

试验工件固定，百叶轮旋转且沿X轴平动，属于干式顺抛，试验现场如图6所示。根照上述步骤按照表1中工艺参数做25组试验，试验所采用的工艺参数组合及相关结果如表2所示。图6右下角为抛光一次百叶轮的运行轨迹，1为沿对刀后Z轴运行设定的压缩量距离；2为抛光过程，前半段和后半段百叶轮与试块不接触，只有中间一段进行实际抛光；3为退刀；4为回程。图6左下角为定义的工件坐标系，其原点位于工件表面中心处。试验中，每组工艺参数连续在同一表面区域沿同一进给方向进行2～4次抛光，这是由于抛光2～4次后百叶轮磨损导致抛光效果降低，表面粗糙度趋于稳定，增加抛光次数不能降低粗糙度。主轴转速和压缩量对百叶轮的磨损量影响明显，主轴转速和压缩量越大，百叶轮磨损越快，其中压缩量的影响最明显，因此在压缩量为1.5 mm时抛光2次，压缩量为1.0 mm时抛光3次，压缩量为0.5 mm时抛光4次。如果工艺参数合理，则抛光后可去除铣削后产生的表面波纹，从而提高表面粗糙度，改善表面残余应力，提高表面质量。

2.3 接触弧长的计算

由图7和图8所示的抛光模型图可知，若试件宽为b，则因为百叶轮柔性原理，柔性抛光状态下的百叶轮变形较大，其实际切入TC4的深度只有几十微米，所以抛光过程的接触弧长近似为直线AB；沿着百叶轮进给速度vw(单位：mm·s-1)的方向抛光一次，图7a中百叶轮B点刚开始接触试块时记为t1，对应计算机采集软件上抛光力信号开始变化(例如图9中t1=3 s)；图7b所示为百叶轮正在抛光试块，当百叶轮运动到图7c位置时记为t2，表示试块A点即将和试块分离，对应计算机采集软件上抛光力信号开始恢复到初始状态(例如图9中t2=14.15 s)；在抛光力持续时间t1～t2内，即百叶轮开始接触试块到和试块分离的这段时间，从点B开始接触试块到点A离开试块的总抛光接触痕迹为接触弧长和试件宽度之和，因此抛光过程中百叶轮和试件的接触弧长

lc=vw(t2-t1)-b。

(1)

式(1)的参考坐标系为图6和图8所示的工件坐标系，其运动方向与X轴正方向一致。按照式(1)计算的接触弧长如表1所示。

2.4 试块抛光后表面粗糙度和残余应力测量

试块抛光之前的表面由数控铣床铣削而成，经过抽样检测可知其表面粗糙度和表面残余应力的一致性较好。抛光后立即测量试块的表面粗糙度和残余应力。

表面粗糙度采用接触式粗糙度仪TA620测量平台进行测量(如图10)，将抛光后的试块置于粗糙度仪测量平台上，调节升降装置与被测试块表面刚好接触，按下测量按钮。测量时粗糙度仪测头要在抛光表面上划过一段直线，测量位置的选择如图11所示，图中虚线表示抛光后的试块表面，虚线走向表示抛光后百叶轮的磨粒在表面划下的沟槽走向，与抛光轨迹一致；与虚线垂直的短横线表示测头测量时划过的痕迹，为了减小测量误差，选取3个测量点L，M，N，以这3个点为中心点各测量两次，求取两次测量值的平均值作为这3个点的测量值，然后求取3个点测量值的平均值作为最终表面粗糙度结果Ra，如表2所示。

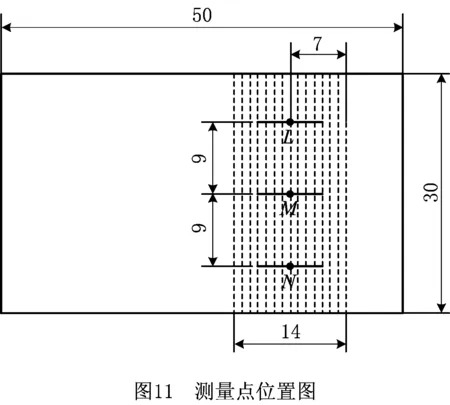
表2 工艺参数及目标参数

续表2

采用PROTO LXRD残余应力测试分析测量系统的表面残余应力，为了保证与表面粗糙度测量点的位置一致，表面残余应力的测量点也选取图11中的L，M，N3点，测量现场如图12所示。测量时先进行对焦，目的是选定测量位置，然后在计算机上点击测量按钮进行测量，由于该测量仪基于X射线散射原理，测量时需注意安全防护。将3个点测得的残余应力求平均值，结果如表2所示。

3 试验结果分析

3.1 单因素试验结果分析

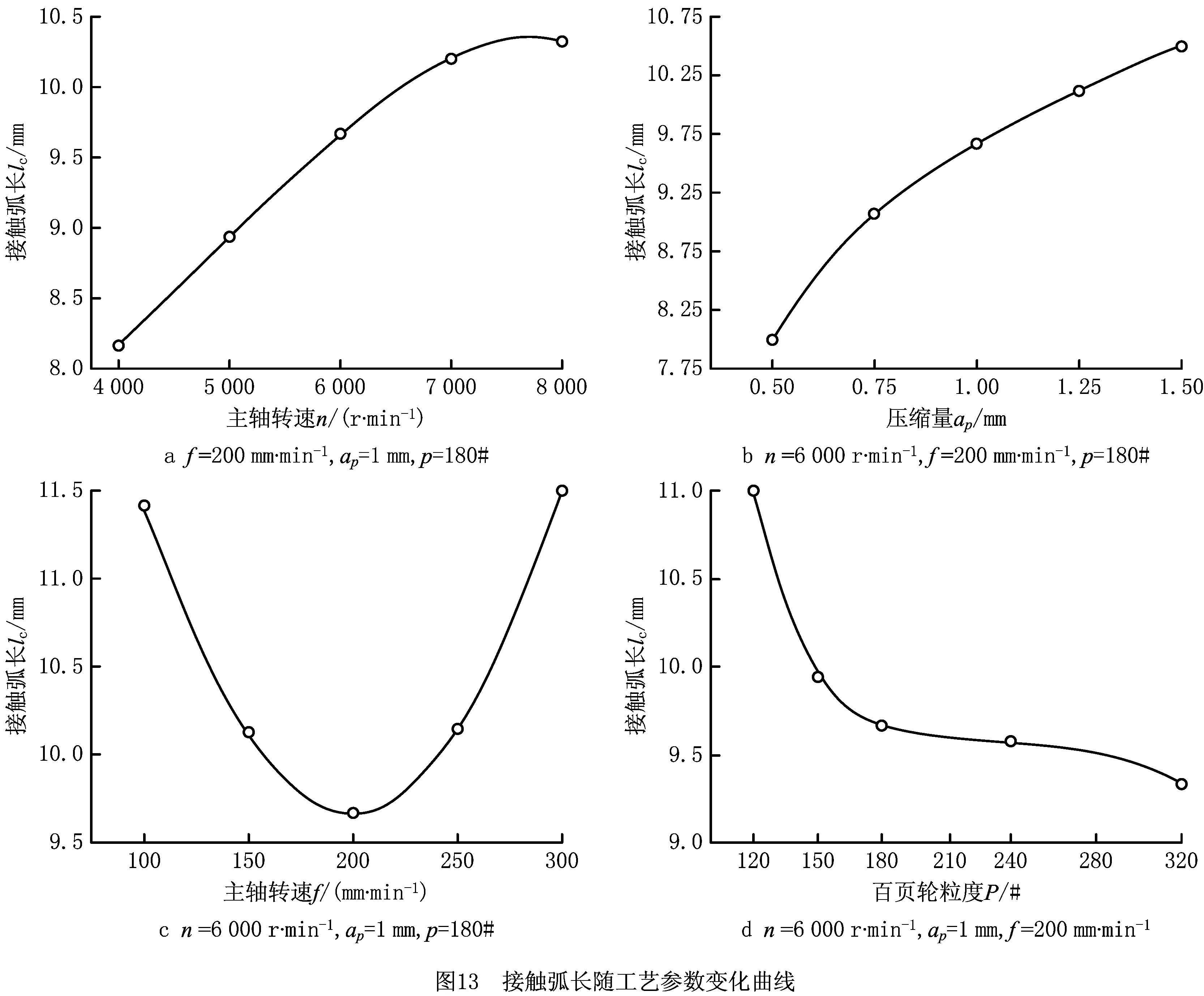
本试验主要考虑主轴转速、压缩量、进给速度和百叶轮粒度4个工艺参数。根据表2的17～25组试验结果，并添加相关工艺参数的试验，经过计算求得单因素变化下的接触弧长，如表3所示。本试验共4个工艺参数，保持任意3个工艺参数不变，令1个工艺参数变化，可得单因素变化下接触弧长的变化规律，采用最小二乘法进行曲线拟合，绘制如图13所示的接触弧长随单一工艺参数变化曲线图，分析可得在本试验条件下：①接触弧长与主轴转速正相关，这是由于主轴转速增大，即百叶轮线速度增大，百叶轮甩开量变大使百叶轮半径变大，变形量也增大，接触弧长自然增大；另一方面，线速度增大导致抛光区温度升高，百叶轮和试块材料均会变软，导致接触弧长增大。②接触弧长与压缩量也为正相关，这是由于压缩量增大时百叶轮的变形量变大，导致接触弧长变大。③接触弧长随进给速度的增大先减小后增大，这是由于当进给速度从100 mm·min-1增大到200 mm·min-1时，在单位时间、单位面积参与抛光的磨粒数减小，去除材料深度降低，导致接触弧长减小；当进给速度由200 mm·min-1增大到300 mm·min-1时，切向抛光力增大，法向抛光力急剧增大，导致百叶轮变形量增大，从而使接触弧长增大。④接触弧长与百叶轮粒度负相关，这是由于随着粒度的增大，百叶轮去除材料的效率降低，实际去除材料深度降低，接触弧长自然减小。

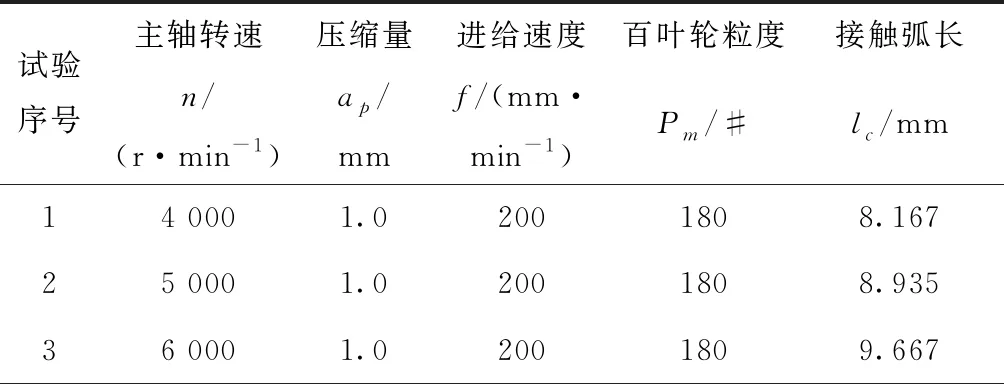
表3 单因素工艺参数及接触弧长计算结果

续表3

3.2 接触弧长的曲线拟合

3.2.1 建立拟合方程

3.1节对接触弧长和工艺参数的定性关系进行了分析，为进一步研究接触弧长和工艺参数之间的定量关系，采用二次多项式拟合接触弧长和工艺参数之间的数学关系式，该方法的拟合精确度高、有效性好，求得拟合方程后通过给定工艺参数可以预测接触弧长。二次多项式回归方程一般表示为

(2)

本文二次多项式的具体表达式为

lc=k0+k1n+k2ap+k3f+k4Pm+k12nap+

k13nf+k14nPm+k23apf+k24apPm+k34fPm+

(3)

式中：ε为随机误差；k0为常数项；k1,k2,k3,k4为一次项系数；k12,k13,k14,k23,k24,k34,k11,k22,k33,k44为二次项系数。

构建函数

(4)

式中：

k13nifi+k14niPmi+k23apifi+k24apiPmi+

(5)

ni,api,fi,Pmi(i=1,2,…,25)为表1中相应的工艺参数组合；lci(i=1,2,…,25)为表1中测得的25组接触弧长数据。令

ki=(k0,k1,k2,k3,k4,k12,k13,

k14,k23,k24,k34,k11,k22,k33,k44)T，

(6)

将表1的数值代入式(4)后，得到关于ki的二次多项式，本文目的就是求ki的值，使函数Q(ki)最小，即非线性函数求极值问题。对于函数Q(ki)，变量ki的最高次数为2，属于二次多项式求极值问题，采用Levenberg-Marquardt算法求该极值问题。

令

(7)

迭代格式为

ki+1=ki+λdi。

(8)

Levenberg-Marquardt算法是对Gauss-newton法的一种修正。对于当前迭代点，Levenberg-Marquardt算法的搜索方向为

(9)

式中：μi≥0；I为单位矩阵；Ji为F(ki)的Jacobian矩阵；Fi为其在ki点的值。

若μi=0，则Levenberg-Marquardt算法变为Gauss-newton法，当μk很很大时，Levenberg-Marquardt算法接近梯度下降法，可见Levenberg-Marquardt算法同时具备了Gauss-newton法和梯度下降法的优点，因此收敛速度更快。

令迭代初始点k0=(0,1,1,1,1,1,1,1,1,1,1,1,1,1,1)T，在Minitab软件中选择Levenberg-Marquardt算法求解本文的非线性函数求极值问题，置迭代终止规则为|di|≤ε=10-6。迭代14次后可得

k3=(4.619 37,0.002 01,9.360 65,-0.062 38,

-0.018 89,-0.000 17,4.162 50×10-7,

-1.352 35×10-7,-0.008 54,-0.005 60,

-1.269 1×10-5,-1.099 45×10-7,-1.759 12,

0.000 18,6.116 25×10-5)T。

拟合方程为

lc=4.619 37+0.002 01n+9.360 65ap-

0.062 38f-0.018 89Pm-0.000 17nap+

4.162 50×10-7nf-1.352 35×10-7nPm-

0.008 54apf-0.005 60apPm-1.269 1×10-5

(10)

式中工艺参数和接触弧长的单位均与表2相同。

3.2.2 拟合方程的显著性检验

拟合方程的方差分析结果如表4所示。当置信水平为95%的双侧区间时，接触弧长拟合模型的P<0.000 1，一般认为模型中检验项的P<0.05时说明该项是显著的，否则说明该项不显著，因此该拟合方程非常显著；拟合优度检验统计量R2=0.960 5，调整后R2=0.905 3，非常接近1，表明该拟合方程的拟合度非常好，有效性非常高，该模型可以预测接触弧长。表5所示为验证试验所取的工艺参数以及由工艺参数计算所得的接触弧长，由拟合方程所求的接触弧长预测值和表5验证所得的计算值对比曲线如图14所示，由图可见试验序号为3，6，8的3组残差较大，计算得第3组偏差率为3.82%，第6组偏差率为7.77%，第8组偏差率为3.68%，最大偏差率为7.77%，由此可得拟合值和测算值无明显差异。

表4 拟合模型方差分析表

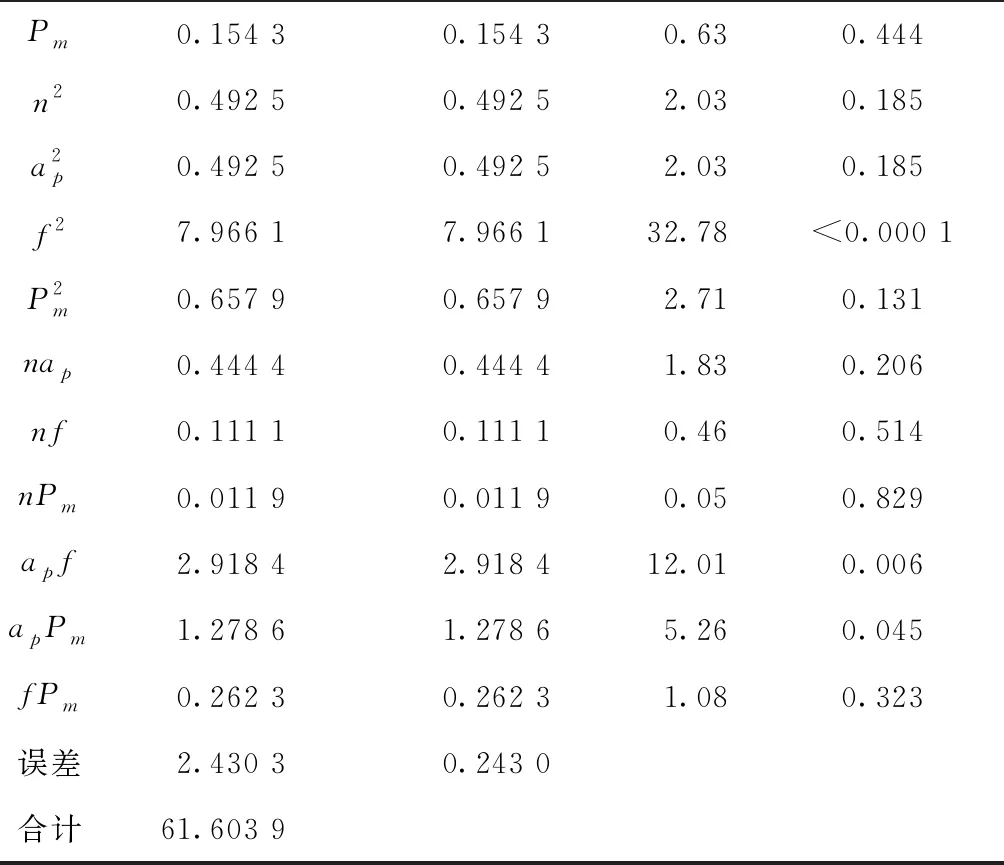
续表4

注：R2=0.960 5；调整后R2=0.905 3。

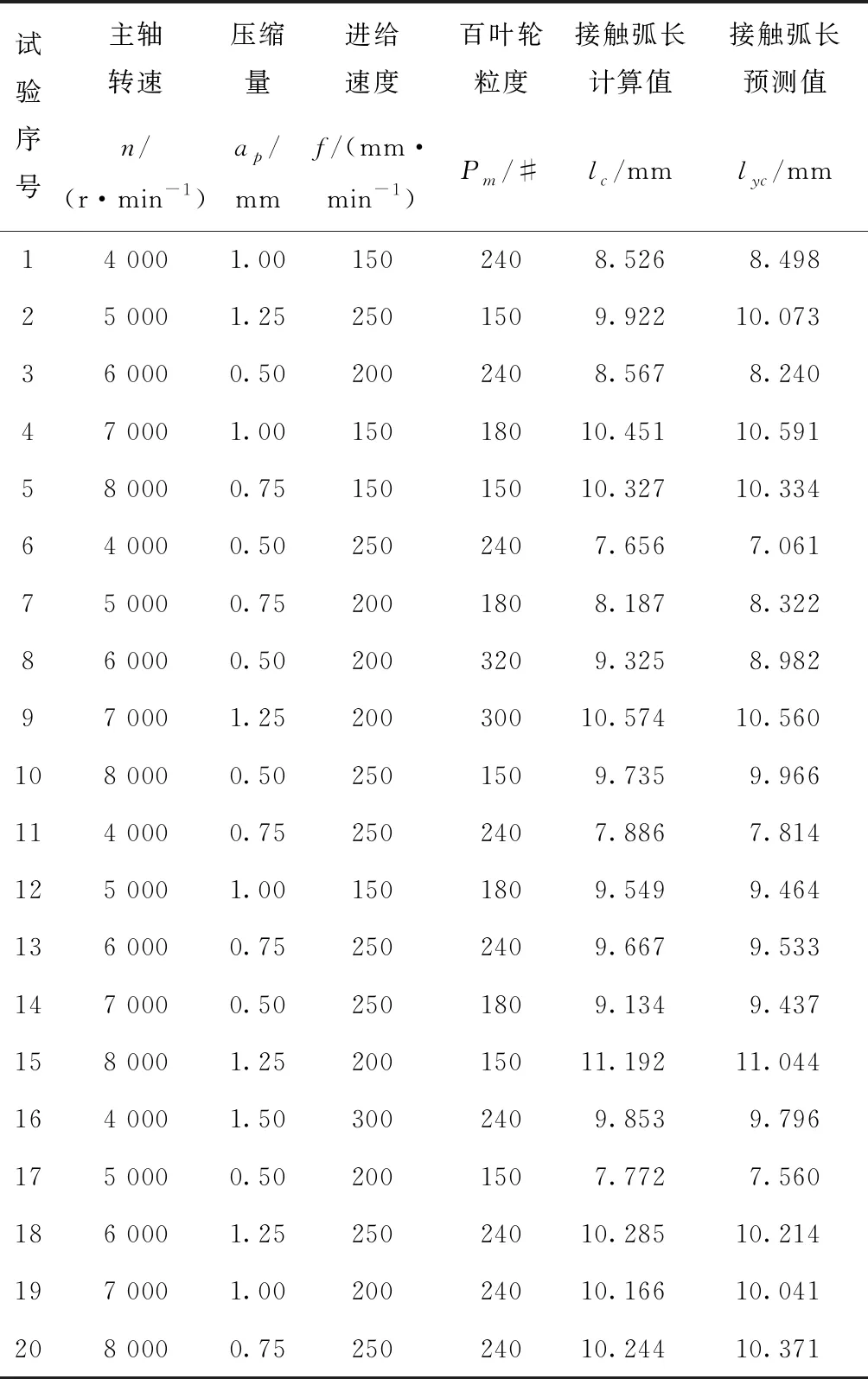
表5 接触弧长的验证结果

对拟合方程中的系数进行显著性检验，结果如表4所示。可见，一次项主轴转速n、压缩量ap的P<0.000 1，平方项f2的P<0.000 1，交叉项apf和apPm的P<0.05。如果模型中检验项的P<0.05，则认为该项是显著的，否则认为该项不显著，以此可以判断n，ap，f2非常显著，交叉项apf和apPm显著，其余项不显著。

3.3 交互作用和主效应分析

3.3.1 交互作用分析

图15所示为以接触弧长拟合均值为响应，主轴转速、压缩量、进给速度和百叶轮粒度为因子的交互效应图，图中纵坐标为拟合均值。当某一因子水平上的响应依赖于其他因子的水平时，表示存在交互作用。在交互作用图中，如果显示的是平行线，则表示不存在交互作用；线偏离平行状态的程度越大，交互作用越大，换言之，交互作用图中各线之间所夹的锐角越大，交互作用越大。由图可见各分图中线所夹的锐角都不大，说明4个工艺参数之间的交互作用都不大。

3.3.2 主效应分析

主效应仅能在交互作用效应不显著或交互作用不大的情况下解释。主效应图显示每个因子水平的响应均值，同时在总均值处绘制一条水平线，效应就是均值(图16各散点纵坐标值)与参考线(图16水平虚线纵坐标值)之差，主效应表征了因子对响应的影响程度。由上述分析可知，本文试验以接触弧长的拟合均值为响应，主轴转速、压缩量、进给速度和百叶轮粒度为因子的交互效应均不大，主效应可以对响应进行解释。由图16的主效应图可以看出，影响均值与参考线之间差值的因子从大到小依次为主轴转速n、压缩量ap、进给速度f和百叶轮粒度Pm，此即为接触弧长效应从大到小的排列；主效应的方差分析结果如表6所示，因为主轴转速n和压缩量ap主效应的P<0.05，所以是显著的，因为进给速度f和百叶轮粒度Pm的主效应P>0.05，所以不显著。综上所述，工艺参数中主轴转速n和压缩量ap对接触弧长的影响较明显，进给速度f和百叶轮粒度Pm对接触弧长的影响不明显。从图16中也可看出，这4个工艺参数对拟合接触弧长均值的影响规律：拟合接触弧长的平均值与主轴转速正相关，与压缩量也为正相关；接触弧长均值随进给速度的增大先减小后增大，随百叶轮粒度的增大也是先减小后增大。除百叶轮粒度外，其余3个工艺参数对拟合接触弧长均值的影响规律与前述工艺参数对计算所得接触弧长的影响规律一致；鉴于拟合方程的拟合度很高，拟合均值随百叶轮粒度的变化规律反映整体变化规律，而前述分析的百叶轮粒度对实测接触弧长的影响规律只是针对5组工艺参数得出的结论，因此认为接触弧长随百叶轮粒度的增大先减小后增大。

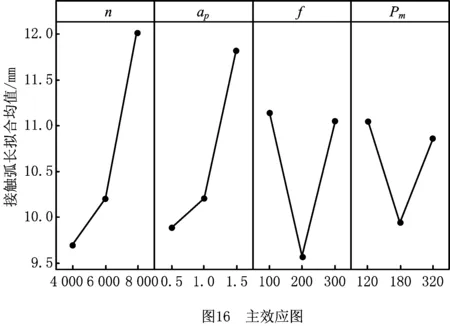
表6 主效应方差分析表

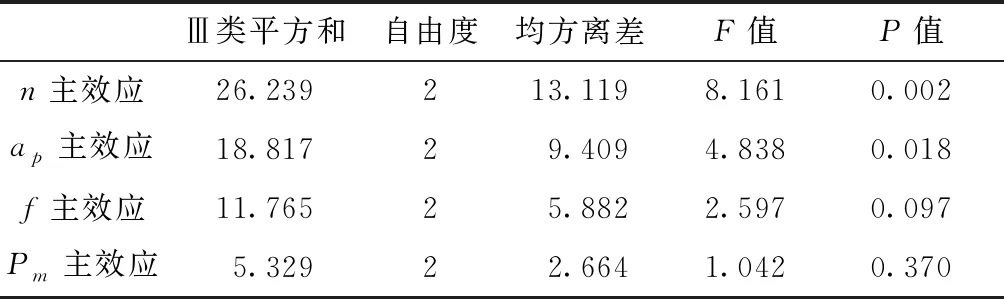
Ⅲ类平方和自由度均方离差F值P值n主效应26.239213.1198.1610.002ap主效应18.81729.4094.8380.018f主效应11.76525.8822.5970.097Pm主效应5.32922.6641.0420.370

3.4 参数优化

利用粗糙度测量仪和残余应力测试分析系统测量抛光后试件表面的粗糙度和残余应力，多次测量后求平均值得到的结果如表2所示，然后以计算的接触弧长为因子，以表面粗糙度和表面残余应力为响应，绘制表面粗糙度和表面残余应力随计算的接触弧长变化的散点图和拟合曲线(如图17和图18)，经过2次重复验证发现绘制的散点图和拟合曲线几乎不变，试验重复性较好。然而，观察图17和图18发现，其离散区域较大，原因是：①接触弧长在测算时会出现误差，表面残余应力与表面粗糙度的测量设备和测量方法存在误差，抛光时的机床、装夹、抛光杆抛光一段时间后的变形、抛光轮的制造过程、TC4试块表面不同部位等均存在误差，环境温度和湿度等造成误差，以及上述各种误差之间存在有耦合误差；②表面残余应力和表面粗糙度的影响因素较多，接触弧长并不一定是最显著的影响因素，接触弧长的变化由主轴转速、压缩量、进给速度和百叶轮粒度等的变化导致，这些因素可能是以上两个因子最显著的影响因素，这些原因共同导致图17和图18的离散度较大。

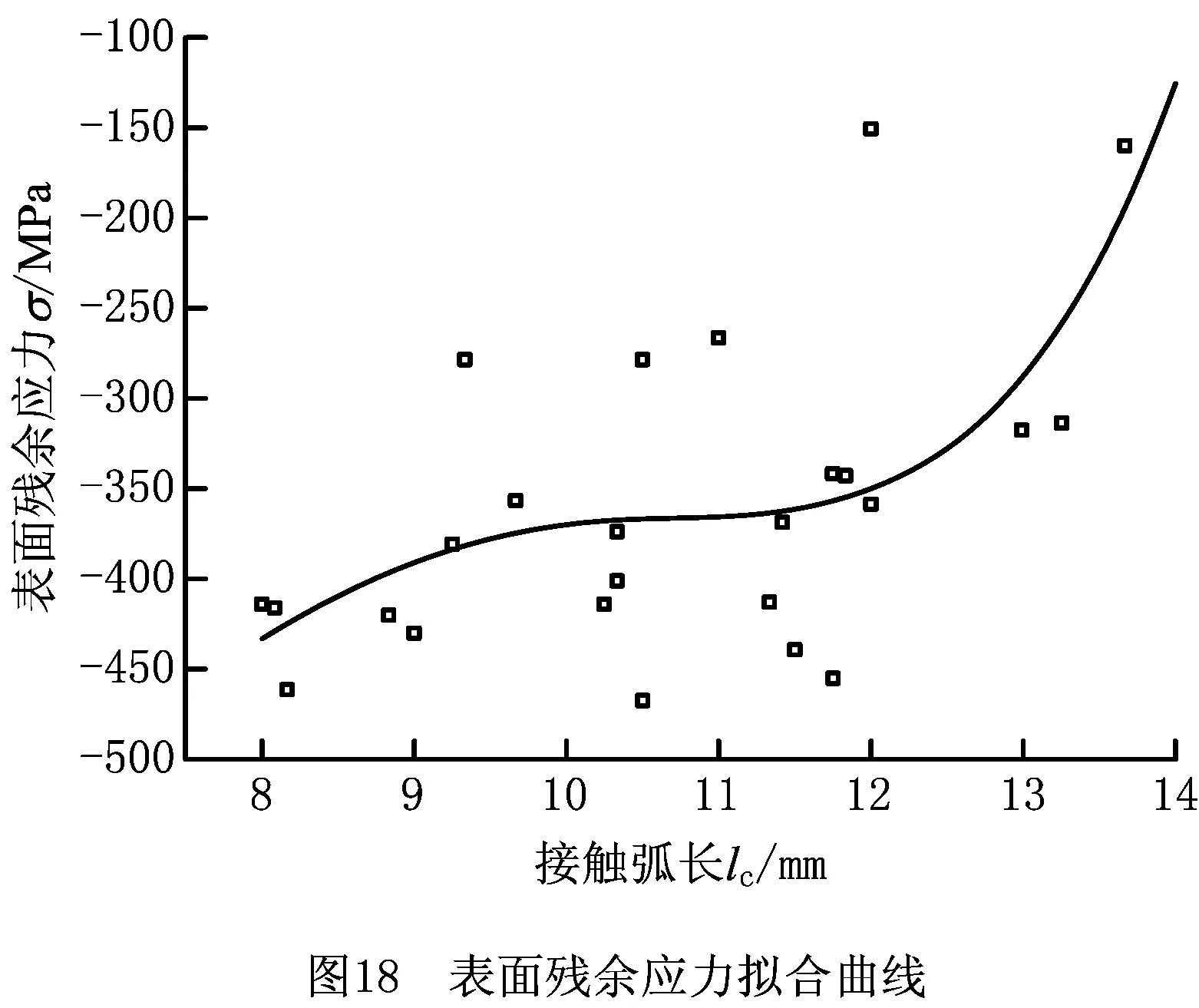
图18纵坐标中正值表示残余拉应力，负值表示残余压应力，其值越小，绝对值越大，表示残余压应力越大。

零部件加工后的表面质量包括微观几何形貌和物理性能，微观几何形貌主要指表面粗糙度，物理性能则包含表面残余应力、加工硬化等，两者对零部件的疲劳强度有很大影响：表面粗糙度微观波谷在交变载荷条件下会引起应力集中，进而引起疲劳裂纹，粗糙度越大，抗疲劳破坏能力越差；表面残余压应力能延缓疲劳裂纹的产生和扩展，提高疲劳强度，残余拉应力容易引起零件表面晶间破坏，从而产生表面裂纹，进而降低疲劳强度[24]。

综上所述，表面粗糙度越低，表面残余压应力越大，零件的疲劳强度越高。为了优化工艺参数，提高抛光表面质量，以接触弧长为因子，考虑优化问题

(11)

图17和图18所示分别为试块抛光后表面粗糙度和表面残余应力关于计算所得的接触弧长的4次拟合曲线，虽然拟合残差较大，但是从图中可得，总体上表面粗糙度和表面残余应力随接触弧长的增大而单调递增，为正相关关系。因此对于式(11)的优化问题，在本试验条件所限定的工艺参数范围内，当接触弧长最小时，表面粗糙度最低，表面残余压应力最大。

上述优化问题可以转换为以下约束优化问题：

minlc(n,ap,f,Pm)=lc=4.619 37+0.002 01n+

9.360 65ap-0.062 38f-0.018 89Pm-

0.000 17nap+4.162 50×10-7nf-1.352 35×

10-7nPm-0.008 54apf-0.005 60apPm-

1.269 1×10-5fPm-1.099 45×10-7n2

4 000r·min-1≤n≤8 000r·min-1;

0.5 mm≤ap≤1.5 mm;

100 mm·min-1≤f≤300 mm·min-1;

120#≤P≤320#。

(12)

采用MATLAB求解该优化问题得理论解为(n,ap,f,Pm)=(4 000 r·min-1,0.5 mm,190.8 mm·min-1,201,2#),minlc=6.377 0 mm，主轴转速、压缩量和进给速度的最优解数值均可通过程序实现，而工艺参数中百叶轮粒度只能选取80#，100#，120#，150#，180#，220#，280#，240#，320#等离散值，求得理论最优解为190.8#，实际中最靠近最优解的粒度号为180#和220#，这两个粒度可以形成两组工艺参数组合，两组工艺参数及其对应的接触弧长如表7所示。由表7可知实际最优解为第2组工艺参数，对应的最优接触弧长为6.398 6 mm。

表7 两组工艺参数的接触弧长对比

用上述求得的最优工艺参数进行实际抛光验证，得到的测量结果如表8所示。

表8 最优工艺参数验证结果

表8中最优工艺参数组合下测得的接触弧长为7.261 mm，与理论计算值6.398 6 mm相差13.5%，工程实际中理论值与实际值相差30%以内都认为是正常的，因此理论与验证结果无明显差异，表明理论优化的结果与试验一致性较好，而且此时测得的粗糙度和残余应力与表2相比较小，说明上述分析的结论是可靠的。

4 抛光力和抛光温度与接触弧长的关系

4.1 抛光力对接触弧长的影响

图9所示为表1中第17组试验参数下的抛光力信号，可见X，Y，Z3个方向的初始力不为零，这是由于夹紧力的缘故；抛光过程中，百叶轮的切入持续时间段为3 s～4.55 s，切出持续时间段为12.75 s～14.5 s，由于这两段时间属于百叶轮和试块的冲击接触和分离阶段，抛光力波动较大，4.55s～9.5s时间段为百叶轮磨粒剧烈磨损阶段，抛光力波动次之；9.5 s～12.75 s是稳定抛光阶段，抛光力波动较小，抛光力波动因百叶轮每个叶片和试块不断接触与分离造成。

由上述分析可知，9.5 s～12.75 s是稳定抛光阶段，抛光力波动较小，故取该时间段的平均抛光力为抛光力的测量结果，按照其中X轴向测得的结果为切向抛光力，Z轴向为法向抛光力。同理，可得其他工艺参数组合条件下的抛光力，其结果如表9所示。

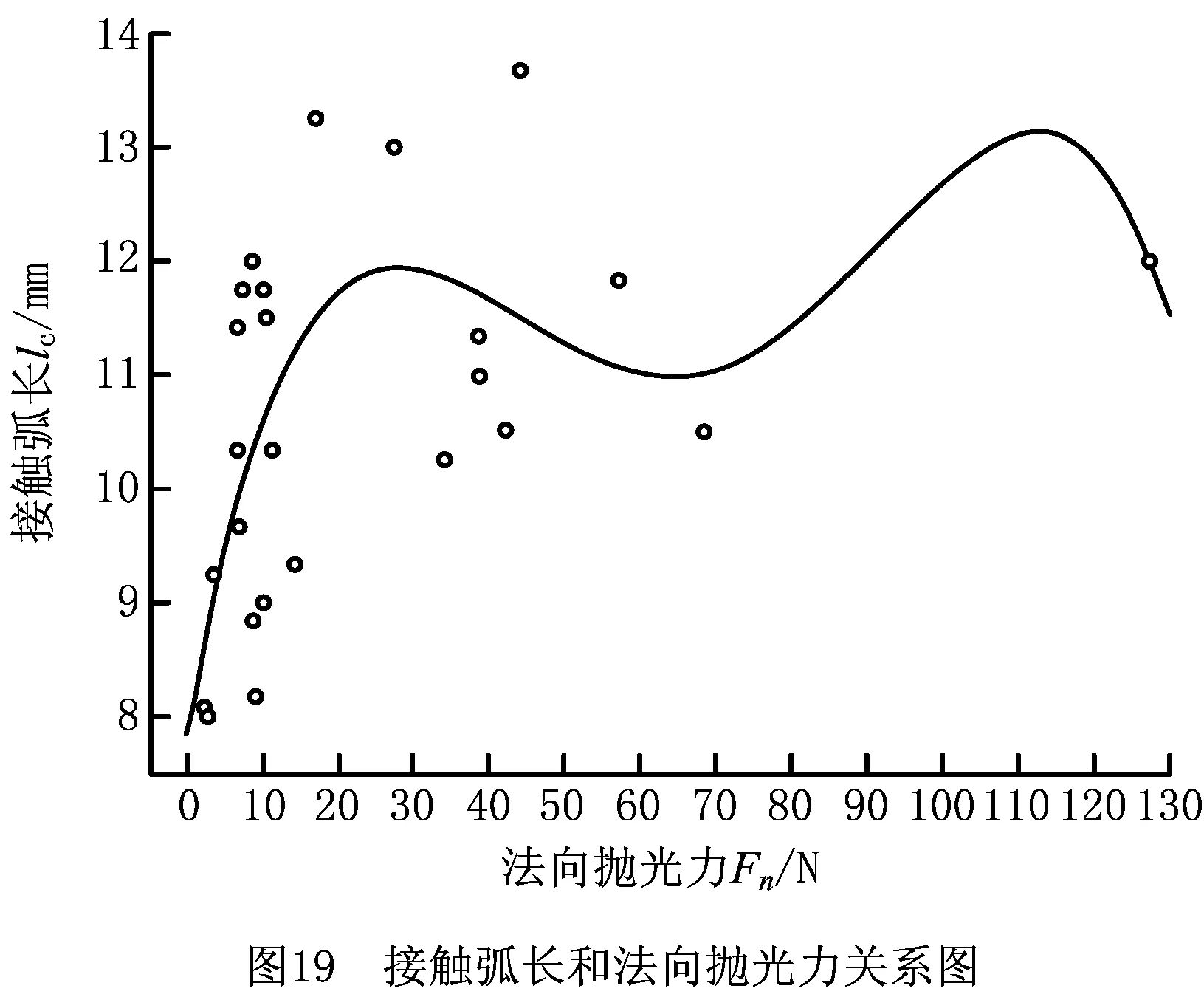
根据表9测量结果，同一组工艺参数下法向抛光力和切向抛光力的比值Fn/Ft在[1,1.8]之间，近似于线性关系，法向抛光力和切向抛光力对接触弧长的影响规律一致，故仅研究法向抛光力对接触弧长的影响规律即可，绘制法向抛光力和接触弧长散点图以及4次拟合曲线如图19所示，经过2次重复验证发现散点图和拟合曲线变化较小，试验重复性较好。观察图19发现，抛光力和接触弧长散点图的离散区域较大，原因是：①试验同样存在3.5节所述的各种误差；②接触弧长最显著的影响因素并不一定是抛光力，而是主轴转速、压缩量、进给速度和百叶轮粒度等其他因素，这些原因共同导致图19的离散度较大。

根据图19可知，70 N～120 N没有对应的弧长值，这段曲线拟合的准确性较差，然而从总体变化趋势来看，接触弧长和法向抛光力正相关，随着法向抛光力的增大，接触弧长随之增大，这是由于增大抛光力会增加百叶轮的变形量，从而使接触弧长变大。

4.2 抛光区温度对接触弧长的影响

采集完表2中第17组试验参数下的热成像图片后，为了和所测量的抛光力测量时间对应，选取图9中t=11.4 s时刻的热成像图片测量图8所示的百叶轮和试块接触点O点的温度值，热成像图片与所测温度值如图20所示，对所测量的温度值进行标定后可得其真实温度如表9所示。同理，测量25组工艺参数下O点的温度值，如表9所示。绘制O点的温度值和接触弧长的散点图以及4次拟合曲线，如图21所示，经过2次重复验证发现绘制的散点图和拟合曲线变化较小，试验重复性较好。然而，由图21可见，温度值和接触弧长散点图的离散区域较大，原因是：①试验同样存在3.5节中所述的各种误差；②接触弧长的最显著影响因素并不一定是抛光温度，而是主轴转速、压缩量、进给速度和百叶轮粒度等其他因素，这些原因共同导致图21的离散度较大。

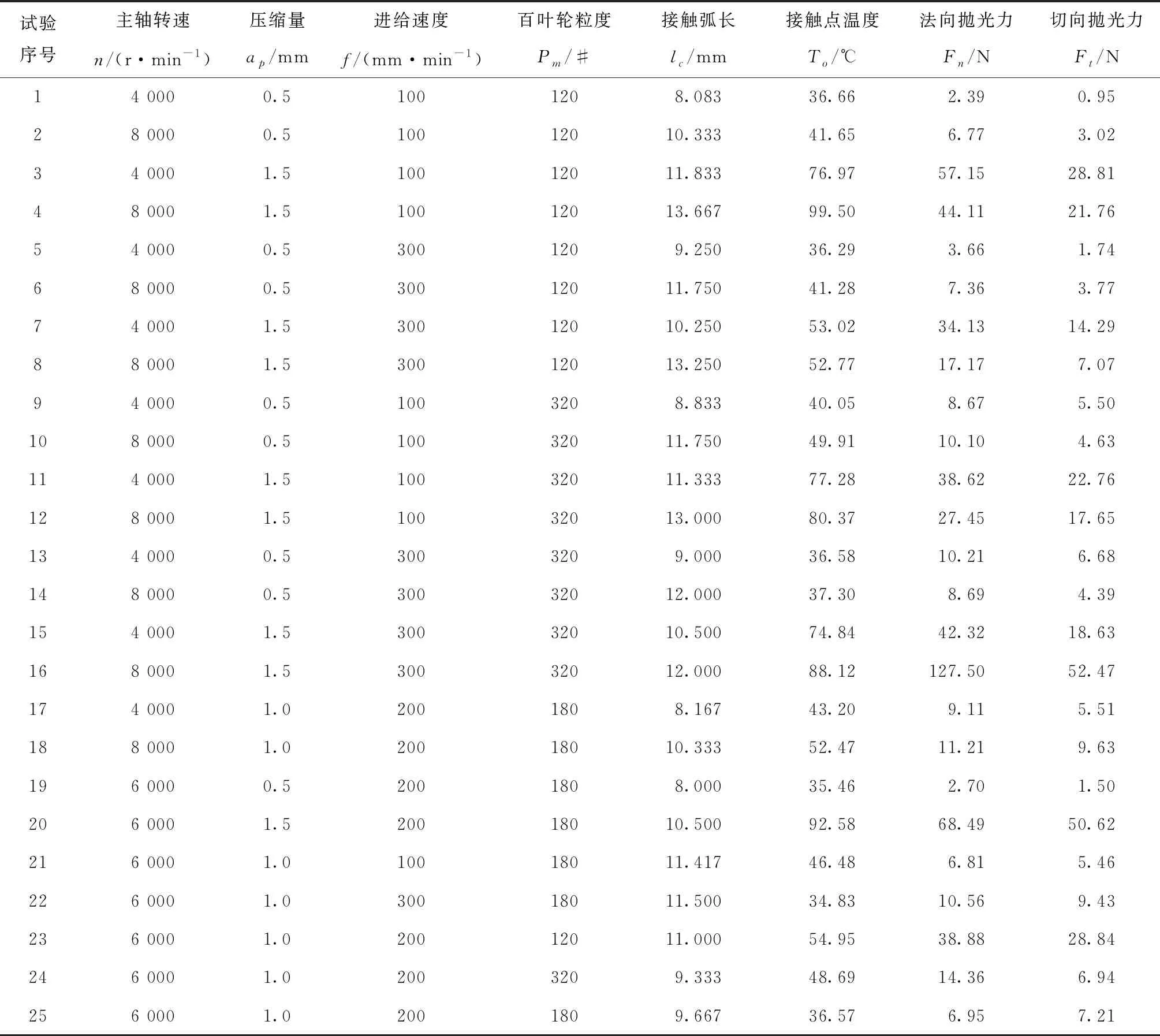
表9 工艺参数与对应的接触弧长、抛光力和抛光温度

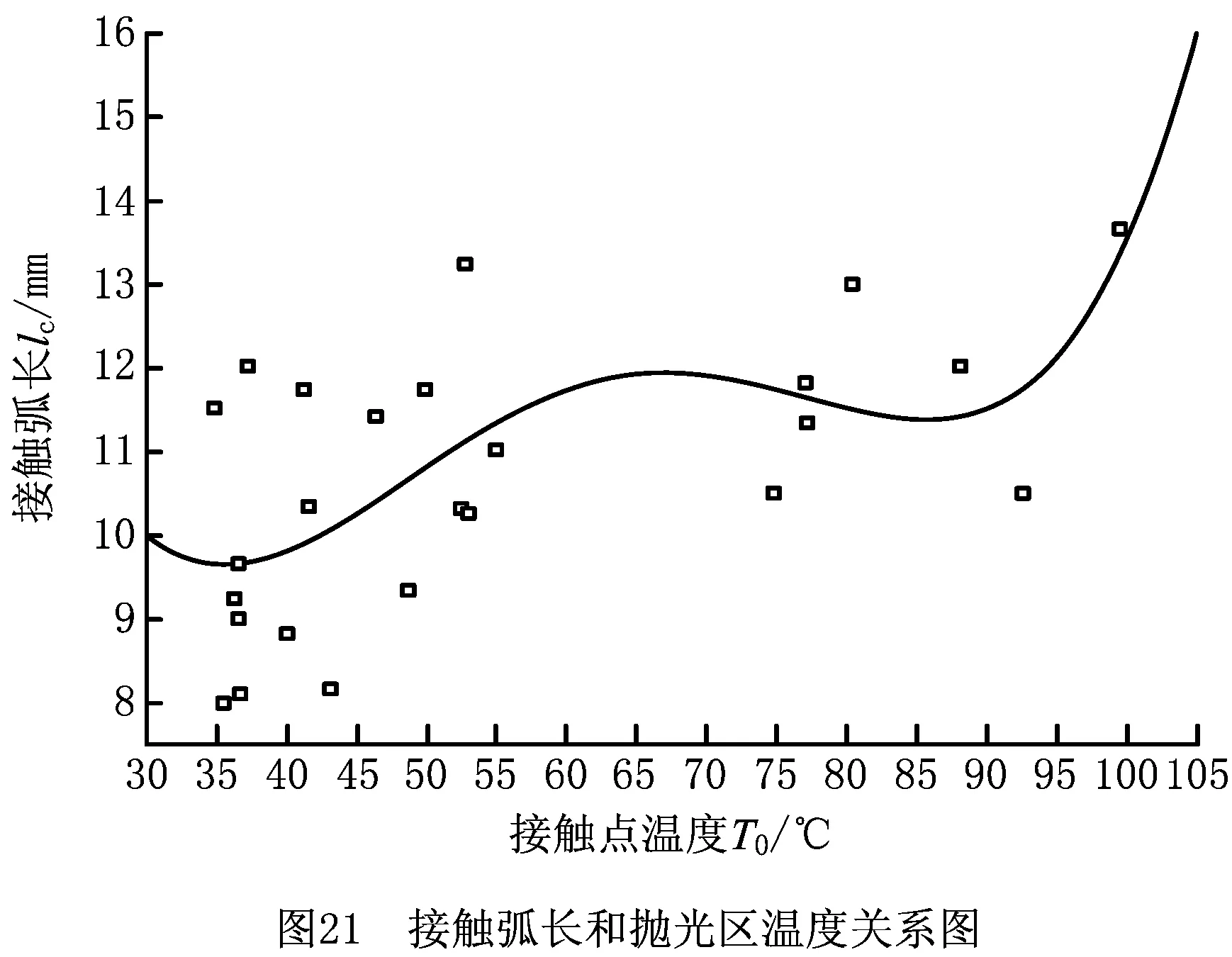
根据图21可知，从总体变化趋势来看，接触弧长和O点的温度值正相关，随着抛光区温度的升高，接触弧长随之增大，这是由于温度的升高会导致百叶轮和试块材料变软，二者变形量同时增大，接触弧长自然变大。

由表9可知，法向抛光力和O点的温度值亦正相关，具有相同的变化趋势，这是由于抛光力增大会使摩擦力做功增加，从而使抛光区温度升高，增大的抛光力和升高的抛光温度会共同促使接触弧长增大。

5 结束语

磨削和抛光过程的接触弧长对加工过程的力热特性和加工后的工件表面质量有重要影响，研究接触弧长对提高工件质量和优化加工工艺意义重大。本文给出一种接触弧长的计算方法，主要研究了接触弧长和主轴转速、压缩量、进给速度和百叶轮粒度4个工艺参数之间的定性和定量关系。以接触弧长为响应，工艺参数为因子，进行了工艺参数主效应和交互作用分析，并以表面粗糙度和残余应力为目标函数，根据接触弧长和工艺参数之间的二次表达式进行工艺参数优化，求得了优化结果。另外，本文还研究了接触弧长与抛光力和抛光温度的定性关系。具体贡献如下：

(1)利用抛光时力信号的持续时间计算求得接触弧长，利用最小二乘原理和Levenberg-Marquardt方法求得接触弧长关于主轴转速、压缩量、进给速度和百叶轮粒度的二次多项式拟合方程；计算得拟合优度检验统计量R2=0.960 5，调整后R2=0.905 3，表明该回归模型拟合度非常好，有效性非常高；对拟合方程中的系数进行显著性检验，结果表明一次项n，ap和平方项f2非常显著，交叉项apf，apPm显著，其余项不显著。

(2)通过试验数据对4个工艺参数的主效应和交互作用进行了分析，结果表明：4个工艺参数之间的交互作用都不大；通过主效应分析可知试验中对接触弧长影响明显的工艺参数为主轴转速n和压缩量ap，进给速度f和百叶轮粒度Pm对接触弧长影响不大。

(3)通过单因素实验分析和主效应分析可知，4个工艺参数对接触弧长的影响规律：拟合接触弧长与主轴转速正相关；接触弧长与压缩量之间正相关；接触弧长随进给速度的增大先减小后增大，随百叶轮粒度的增大先减小后增大。

(4)分析可知表面粗糙度和表面残余应力与接触弧长正相关，当接触弧长最小时，表面粗糙度最低，表面残余压应力最大；以接触弧长为响应，工艺参数为因子，在本试验的工艺参数取值范围内，建立接触弧长最优化问题并求解，得到最优工艺参数为(n,ap,f,Pm)=(4 000 r·min-1,0.5 mm,190.8 mm·min-1,201,2#)，最优接触弧长为6.377 0 mm，并对最优工艺参数进行了验证，结果表明理论优化的结果与试验一致性较好。

(5)研究了抛光力和抛光区温度对接触弧长的影响规律，得到接触弧长与抛光力和抛光区温度总体上正相关的结论。

本文研究了百叶轮抛光平面轮廓的接触弧长，并得到了一些结论，然而百叶轮具有一定柔性，应用于抛光航空发动机和燃气轮机叶片等自由曲面零件时，需要对抛光曲面过程的接触弧长以及力热特性、抛光质量进行进一步研究；同时，还需要研究接触弧长与力、热和表面质量的定性与定量关系，以改善加工工艺，提高加工质量。