航空发动机“空-空-油”螺旋套管换热器夹层传热数值模拟
2020-06-12蒙建成刘少北鲍泽威黄卫星
蒙建成,刘少北,鲍泽威,黄卫星
(四川大学化学工程学院,成都 610065)
航空发动机是飞机的“心脏”,对航空工业具有重大意义。而航空发动机的运行与流体的流动、传热以及燃料燃烧等密切相关,因此,在一定程度上可以将其视作一个小型的“化工厂”。
涡轮叶片是航空发动机的核心部件,提高涡轮叶片的耐热性是目前航空发动机性能提升的关键点之一。Bruening 和Chang[1]提出,通过外涵道空气或者航空煤油RP3 作为冷却介质,降低空气(该空气用于冷却涡轮叶片)的温度,从而提高涡轮叶片的冷却效率,该技术被称为CCA(Cooled Cooling Air)技术。要实现CCA 技术,换热器是至关重要的一环。
本文在CCA 技术的基础上,提出一种全新的航空发动机CCA 换热器——“空-空-油”螺旋套管换热器。该换热器与传统CCA 换热器最大的不同是采用了双冷源的冷却结构:需冷却的空气走夹层,航空煤油RP3 走螺旋内管,外涵空气在换热器外,如图1 所示。双冷源同时冷却空气,冷却效率高,同时,RP3 也得到了预热,使其在燃烧室内燃烧更加充分。除此之外,空气可在螺旋结构内产生二次流,换热效率得到提高,而螺旋管结构本身紧凑、承压抗热冲击性能好,因此,“空-空-油”螺旋套管换热器应用在涡轮叶片冷却上是极具前景的。
相较于螺旋管及螺旋管外的流动与传热问题,螺旋夹层研究较少。本文将以某实际工况为例,研究螺旋套管换热器的夹层内的流体在外涵道的流动与传热特性的实际情况。
1 物理模型与数值模拟方法
1.1 物理模型与网格划分
采用Solidworks 建立几何模型,如图2 所示,其中D 为螺旋直径,P 为螺距,do为夹层外径,di为夹层内径,t 为内管厚度,实体部分为流均域。内管内流动介质为航空煤油RP3,夹层内流动介质为空气。在ICEM CFD 中绘制结构化网格,对夹层内边界层与内管边界层进行加密,如图3 所示。由于外涵道需要生成网格数量很大,且进行与螺旋套管的耦合计算难度大,同时考虑到相比于夹层内空气,外涵道空气流量大,温度变化小,并且本文主要研究螺旋夹层内空气的传热规律,因此不对外涵道与外管进行网格生成,将夹层外侧视为恒壁温条件来简化计算,固体材质采用钢,网格整体模型如图4 所示。模型结构参数如表1 所示。

图1 双冷源螺旋套管换热器原理图Fig.1 Schematic diagram of double-pipe helical heat exchanger with double cooling medium

图2 螺旋套管结构图Fig.2 Structure of double-pipe helical heat exchanger

图3 网格局部模型Fig.3 Local model of mesh

图4 网格整体模型Fig.4 Overall model of mesh
1.2 计算方法与边界条件定义
将网格导入Fluent 16.0 中求解。以Ito 的公式[2]计算表2 中的螺旋夹层及螺旋内管的临界雷诺数Recr,除结构5 在11 g/s 的气量下,其螺旋内管Re 略小于临界值Recr,其他结果均大于Recr,因此认为采用RNG k-ε 模型进行计算是可靠的。在压力速度耦合的方式下采用SIMPLE 算法在进行稳态计算,简化外涵道,故将夹层外侧均设为恒壁温484.5 K[3],该温度为外涵道空气进口温度,状态参数由工况决定,并初步设计以下操作参数进行研究,具体情况如表2所示。表中逆流的定义,是夹层空气的流动方向,同时与RP3、外涵空气的流动方向相反。
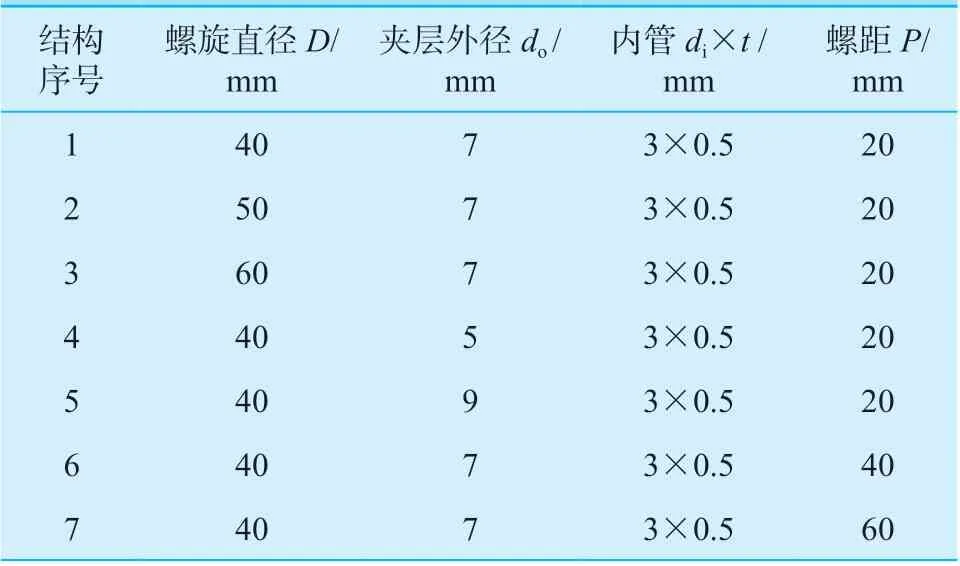
表1 换热器结构参数Table 1 Structural parameters of heat exchanger

表2 换热器操作参数Table 2 Operating conditions and operating parameters of heat exchanger
1.3 模型验证
夹层内流动介质为空气。由于SRK 方程对气体的密度计算结果较为准确,故密度采用SRK 方程计算,其他热物性采用文献 [4]中的数据。内管内流动介质为5 MPa 压力下的航空煤油RP3,采用文献[5]中数据,如图5 所示。可以看到航空煤油RP3 的临界温度在720 K 附近,经过换热后的航空煤油远低于该温度,因此不需要考虑相变所带来的影响。

图5 RP3 的物性图Fig.5 Thermal properties of RP3
由于对双冷源情况下的螺旋夹层换热尚未有文献报道,因此无法直接采用相关传热经验关系式对其进行验证。对于螺旋管的传热研究文献已经较为成熟,因此,采用结构参数为表1 中结构1(无内管)的螺旋管为例进行验证,在1.2 节中所给的实际工况中,采用Roger 的传热经验关系式[6]进行验证。由于公式雷诺数范围所限,因此采用11 ~17 g/s 的气量进行验证。对比结果如图6 所示,可以看到,最大误差为12.5%,在合理范围内,故认为本次模拟方法可靠。

图6 模型验证Fig.6 Model validation
2 计算结果及分析
2.1 流场及温度场分析
以表1 中结构1 的螺旋套管为例,其操作参数以表3 为例进行夹层内流场与温度场分析。图7 为不同转角η 上的螺旋套管换热器流场分布,由于受到离心力的作用,随着流场的逐渐发展,流场的最大速度向螺旋外管外侧偏移,形成内凹的胞体形,速度分布整体呈现外侧高、内侧低的情况,在η=900°时,流场基本稳定,因此认为,此时流场基本上已发展充分。同时发现,在流场周向方向会产生偏转,这种偏转在η<900°时显著存在,在η>900°时并不显著,流动发展不充分会使得流场在周向产生显著偏转。响,呈现外侧高、内侧低的温度分布方式。受流场的影响,截面上的温度分布基本上呈现外侧高、内侧低的趋势,形成内凹的胞体形,并且最高温度区域会在周向方向发生偏转;在η=900°时,温度场分布也基本稳定。从夹层的径向方向来看,温度的降低是从夹层两侧一起降低的,这说明了不论是RP3 还是外涵道空气对传热所产生的影响都是较为显著的。

表3 操作参数Table 3 Operating parameters
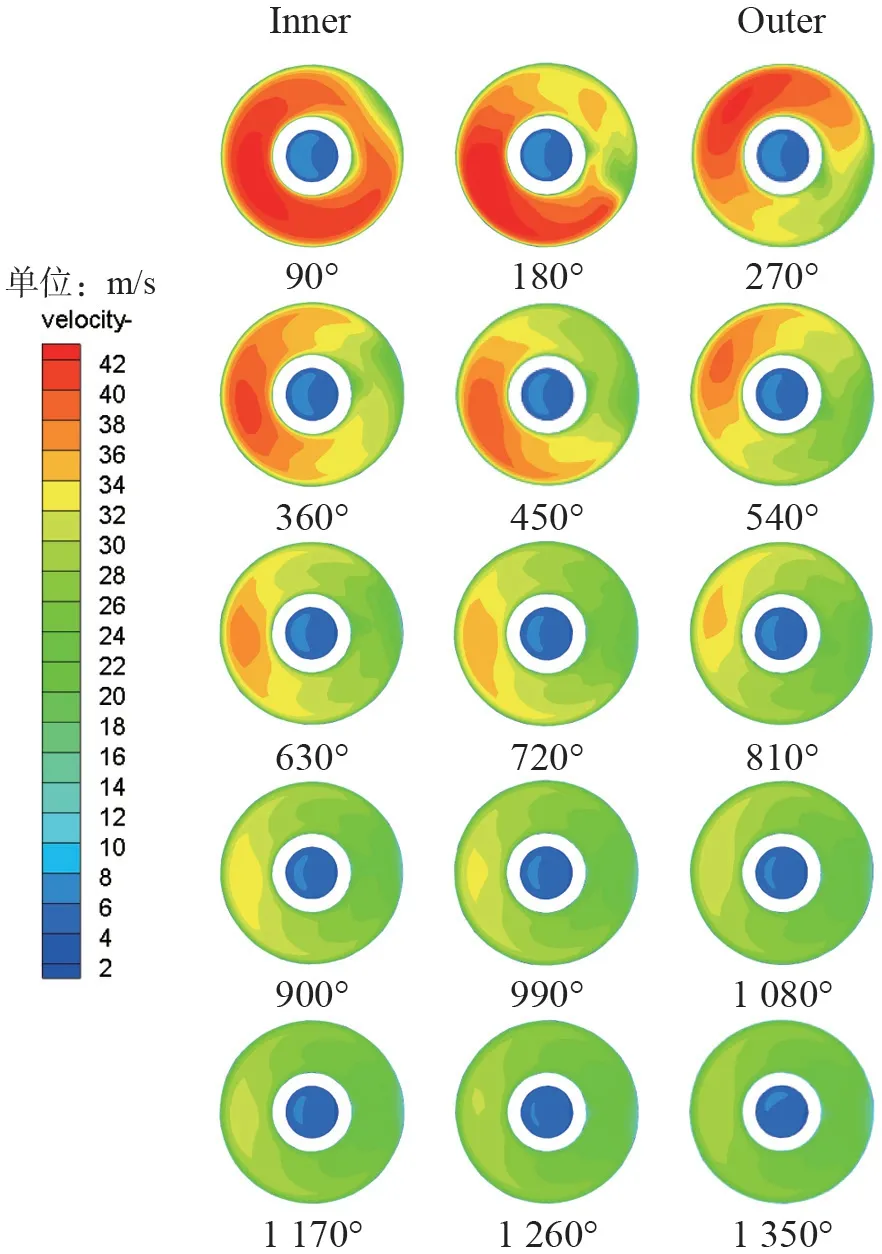
图7 流场Fig.7 Flow field
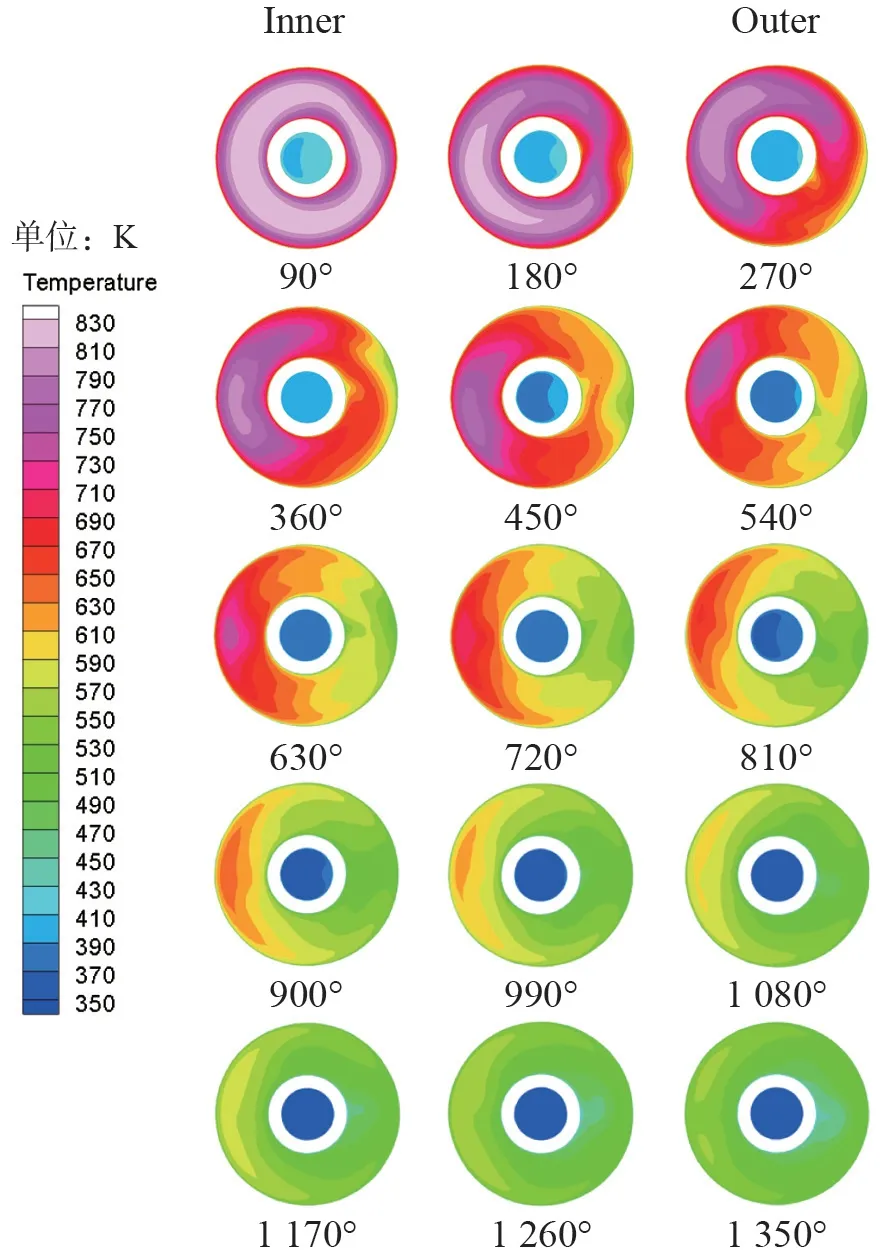
图8 温度场Fig.8 Temperature field
图9 和图10 分别为不同转角的夹层内侧及外侧周向局部换热系数分布图。显然,受离心力的影响,周向局部换热系数都大致呈抛物线分布,且基本在180°附近,即螺旋直径最外侧基本达到最大值,这与流场及温度场所产生的现象一致。并且还发现,当主流速度方向基本与重力方向平行时,hp-in会出现一个波峰,而当主流速度方向基本能与重力方向垂直时hp-in的波峰会出现凹陷,形成双波峰。这说明在重力会对传热产生一定的影响,但不明显,因为凹陷幅度并不大。
图9 夹层内侧周向局部换热系数分布(900°~1 260°)Fig.9 Distribution of circumferential local heat transfer coefficient inside of annulus (900° ~ 1 260° )

图10 夹层外侧周向局部换热系数分布(720°~990°)Fig.10 Distribution of circumferential local heat transfer coefficient outside of annulus (720° ~ 990°)
2.2 几何结构对夹层传热的影响
图11~13 描述了不同结构参数对螺旋管夹层的传热影响,h 为平均传热系数,hin为夹层内侧平均传热系数,hout为夹层外侧平均传热系数。从螺旋直径D 来看,随着螺旋直径从40 mm 变化到80 mm,曲率降低,夹层的传热系数降低。不同螺旋直径的管中其流速基本不变,但会对二次流强度产生较大的影响,曲率越大,二次流强度越高,传热强度越高;从外内径之比do/di来看(内径不变),随着外内径之比从5/3 变化到9/3,夹层的传热系数降低,这是由于外内径之比增大,使得流速大大降低了,流动强度减弱,传热强度下降。螺距从20 mm 变化到60 mm,夹层的传热系数几乎不变,这是由于螺距对于流动强度、二次流影响不大。
2.3 传热经验关联式的拟合

图11 螺旋直径D 对夹层传热系数的影响Fig.11 Effect of diameter of curvature D on heat transfer coefficient of annulus

图12 外内径之比do/di 对夹层传热系数的影响Fig.12 Effect of ratio of do to di on heat transfer coefficient of annulus

图13 螺距P 对夹层传热系数的影响Fig.13 Effect of Pitch P on heat transfer coefficient of annulus
将本文的模拟结果与文献相关关联式进行对比。对于夹层内侧的换热系数,采用文献上螺旋套管夹层传热经验关系式[7]验证;对于夹层外侧的换热系数,由于尚未有文献报道螺旋套管夹层外侧的传热经验关系式,因此采用螺旋管的传热经验关系式[6,8-9]进行验证。
从图14 可以看到,结果的误差大于20%,这是由于文献公式适用范围远低于实际工况要求,同时文献工况与实际工况差距很大;从图15 可以看到,大部分结果的误差超过20%,这说明了螺旋管本身与螺旋套管结构尽管存在相似,但直接采用,仍会存在较大的误差,同时部分公式也存在适用范围过小的原因。因此,不管是夹层内侧还是外侧,现有公式并不足以预测工况下的螺旋套管夹层内的传热系数,需要拟合新的经验关系式,以满足工程实际的需求。

表4 文献公式Table 4 Heat transfer correlation
由前文分析可知,螺距P 对传热的影响可以忽略不计,因此,在进行关联式的推导和拟合过程中,不将螺距P 作为影响因素。最后,将本文的模拟结果拟合成传热经验关系式。
螺旋套管夹层内侧的传热经验公式如下:
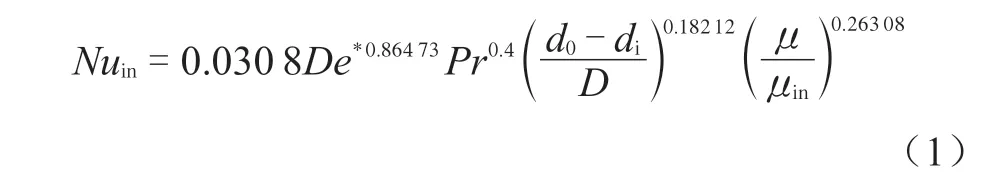
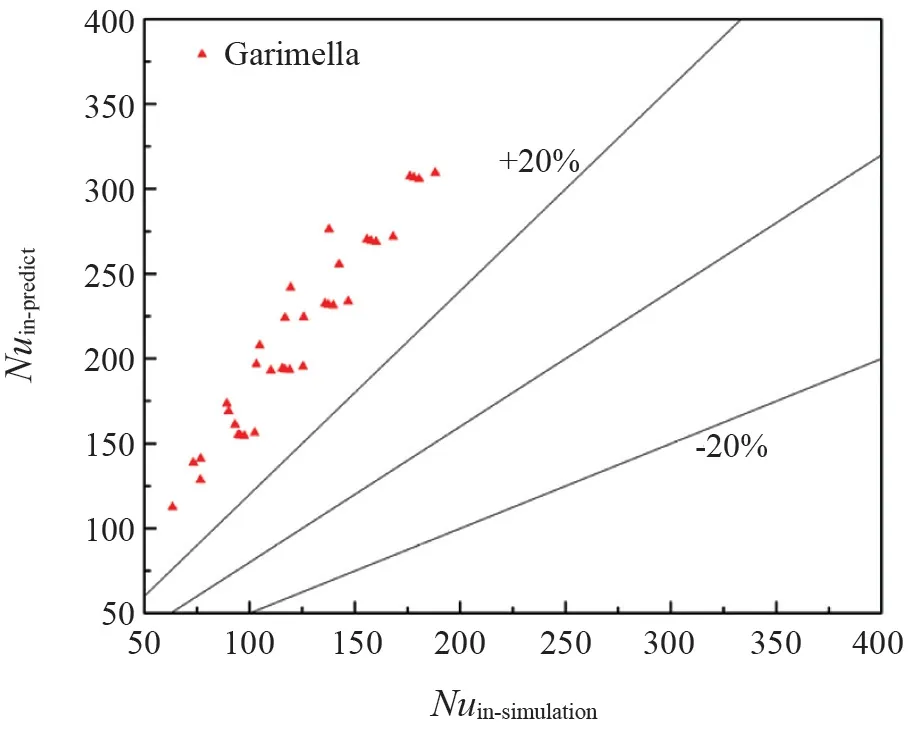
图14 Nuin 与文献传热经验关联式的对比Fig.14 Comparison of Nuin number between simulation data and a previous correlation

图15 Nuout 与文献传热经验关联式的对比Fig.15 Comparison of Nuout number between simulation data and three previous correlations
螺旋套管夹层外侧的传热经验公式如下:

其中:


图16 夹层内侧传热经验关联式误差Fig.16 Comparison of Nuin number between simulated data and calculated data

图17 夹层外侧传热经验关联式误差Fig.17 Comparison of Nuout number between simulated data and calculated data

式中 Nu——努塞尔数;
Pr——普朗特数;
De*——修正迪恩数[10];
ρ——密度;
Cp——比热;
μ——黏度;
k—— 导热系数,定性温度为流体平均温度Tb;
μin——夹层内侧壁面处平均温度下黏度;
μout——夹层外侧壁面处平均温度下黏度;
T1——空气进口温度;
T2——空气出口温度。
公式(1)、(2)的范围如下:
14 000 <De*<39 880,Pr=0.68。
从图16、17 可以看到,夹层内侧、外侧传热经验关系式的误差分别在5%和10%以内,拟合效果非常好,对实际工程设计具有一定的指导意义。
3 结论
(1)受离心力的影响,螺旋套管夹层内的流场与温度场向外侧偏移,在转角达到一定角度后发展充分,流场与温度场稳定。
(2)充分发展后,周向局部换热系数近似呈现抛物线分布,重力会对周向局部换热系数的波峰呈周期性影响,但影响不大。
(3)夹层内传热主要受曲率(do-di)/D 与外内径之比do/di影响,螺距的影响可以忽略不计。
(4)拟合了螺旋套管夹层内的传热经验关联式,对实际设计具有一定的参考价值。
