立式储气罐支承式支座优化设计

2020-06-12苏文献徐伟

化工设备与管道 2020年2期

关键词：封头垫板支座

苏文献，徐伟

（1. 上海理工大学能源与动力工程学院，上海 200093； 2. 上海市动力工程多相流动与传热重点实验室，上海 200093 ）

NB/T 47065.4—2018 《容器支座第4 部分：支承式支座》规定：支承式支座适用于下列条件的钢制立式圆筒形容器：

（1）公称直径DN 800 ～ 4 000 mm；

（2）圆筒长度L 与公称直径DN 之比L/DN 不大于5；

（3）容器总高度H0不大于10 m；

（4）允许使用温度-20 ～ 200 ℃。

立式圆筒形容器及其支承式支座结构如图1 所示。支承式支座作为容器中主要的承受载荷的部件（不做特殊说明本文均指A 型支承式支座），确保整体结构的稳定性和安全性。支承式支座主要由垫板、筋板、底板三部分构成，其中，垫板作为封头与支座相连接的过渡部分，同时起到了减小封头局部应力的作用。在NB/T 47065.4—2018《支承式支座》中，根据计算得到支座本体允许载荷，结合使用容器的公称直径，来选择支座参数尺寸。垫板的尺寸以及结构参数是根据工程经验所定的，并没有严格的数学推理与科学计算，确定的尺寸和参数往往比较保守，有较大的安全余量。如果能够对支座处容器封头局部应力进行详细计算，然后进行应力分类，对分类的应力及其组合进行分类限定，得到垫板的尺寸。这样获得的垫板尺寸比标准给定的尺寸小得多。对批量生产的容器如储气罐来说，能节约较多的材料，减少成本，显著增加企业效益。本文以1.5 m3立式储气罐为例，对容器支座结构进行相关的研究和分析。

图1 几何模型Fig.1 Geometric Model

1 结构参数

本文用于研究的容器为用于储存空气的立式储气罐，有效容积为1.5 m3，封头为标准椭圆形封头，内径为950 mm，外径为959 mm，封头壁厚为4.5 mm；容器设置3 个支座，结构各部分材料参数如表1 所示。

2 有限元分析

2.1 载荷及约束

容器的主要设计工况及载荷如下：工作温度为100 ℃，设计压力为0.84 MPa，储存介质为空气，不考虑其自重。

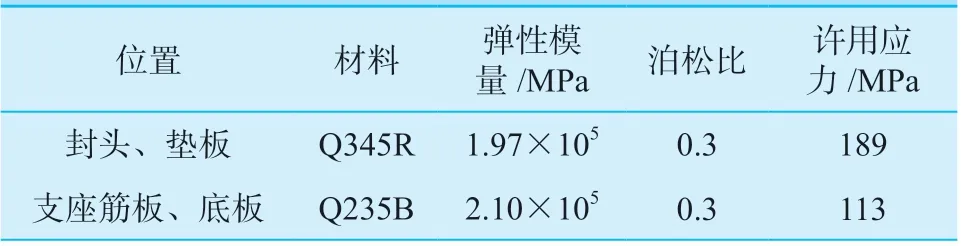
表1 材料参数Table 1 Material parameters

封头局部受力关于轴线中心对称，取1/3 模型进行分析。全模型的有限元计算结果经过计算会比1/3模型的结果略小，所以1/3 模型的结果更加保守，为了优化计算的效率，采用1/3 模型作为本次研究的目标。封头直边段以及两个侧面远离支座反作用的应力集中局域采用环向约束，其他方向自由；封头直边段上侧施加等效端面力Pn：

式中 P0——设计压力；

d——筒体内径；

D——筒体外径。

2.2 有限元模型

在不影响计算结果准确度以及对比性的情况下，根据分析和计算需要，对模型进行了相应的简化：

（1）忽略焊缝的影响；

（2）忽略垫板中心开孔的影响；

（3）忽略下封头中心处远离应力集中区开孔接管的影响；

（4）忽略垫板与封头之间的微小位移，模型接触设置为绑定；

（5）不考虑风载荷和地震载荷的影响。

有限元模拟计算时均采用标准六面体单元SOLID 45 进行网格划分，为了计算的准确性和可靠性，模型封头和垫板的厚度方向网格都进行了三层细化。

支座模型由ANSYS Workbench 中的Design Modeler 模块建立，模型网格如图2 所示。

2.3 有限元应力分析结果

模型在施加约束、载荷之后的计算结果如图3所示。由图3 可以看出：支座的应力集中区域出现在垫板与封头接触的外侧端点处，等效应力最大值为320.97 MPa。

按照JB 4732—1995《钢制压力容器——分析设计标准》规定，对各应力强度的控制值有如下要求：

图2 支座模型网格Fig.2 Support model grid

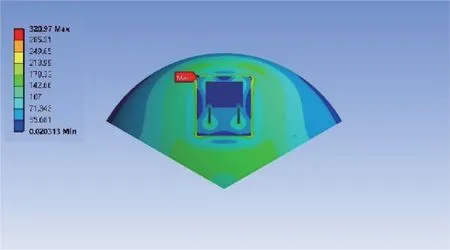
图3 支承式支座模型应力云图Fig.3 Model stress nephogram

一次局部薄膜应力强度SⅡ许用值为1.5 KSm，即：SⅡ≤1.5 KSm。

一次加二次应力强度SⅣ许用值为3 KSm，即：SⅣ≤3 KSm。

式中 K— —各种载荷组合系数，本文K=1；

Sm––––– 材料在设计温度下的许用应力强度，

Sm= 189 MPa。

对支座进行应力评定，路径PATH 见图4。应力评定线上的薄膜应力为一次局部薄膜应力，其强度用1.5 KSm进行限制；在该应力评定线上存在弯曲应力，属于二次应力，它与一次局部薄膜应力之和的强度用3 KSm限制；这两个应力限制条件要求同时满足。应力线性化评定结果见表2。

根据以上标准进行校核：

一次局部薄膜应力强度

一次加二次应力强度

校核结果表明该结构的一次局部薄膜应力以及一次加二次应力均合格，符合安全要求。

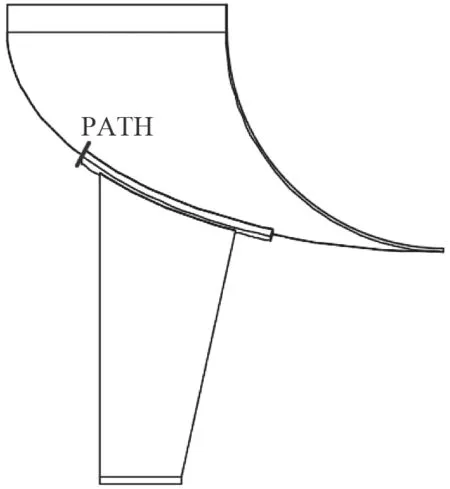
图4 应力线性化路径Fig.4 Stress linearization path

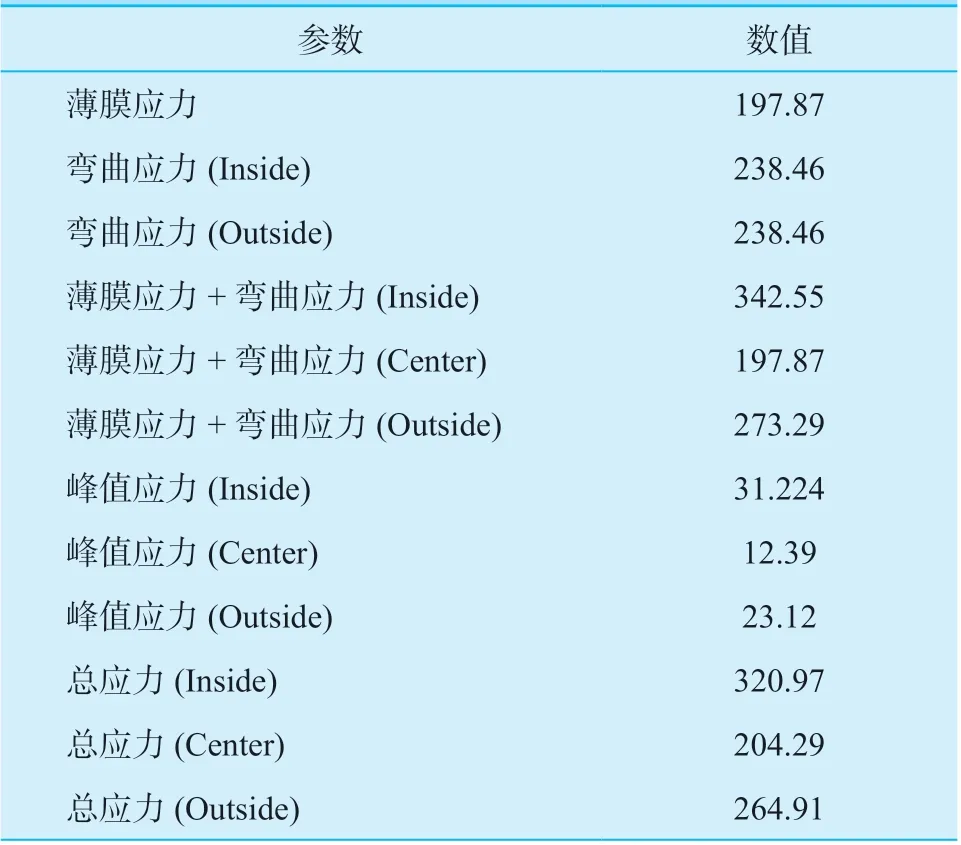
表2 应力线性化结果Table 2 Stress linearization results MPa

3 支座优化设计

本文支承式支座的优化方案主要是从垫板的结构以及尺寸方面进行改进优化，各变量几何含义如图5 所示。

（1）结构改进型：对垫板距离封头中心线的距离V6进行改进，讨论不同垫板位置对封头局部应力的影响；

（2）尺寸改进型：对垫板的三维尺寸，即长V1、宽H2、厚度FD1进行优化改进，讨论其不同垫板尺寸对封头局部应力的影响；

（3）结构与尺寸改进型：将上述（1）、（2）两种方案同时进行讨论改进，研究其最优化方案。

3.1 目标函数设置

支承式支座优化问题可表示为如下的数学优化

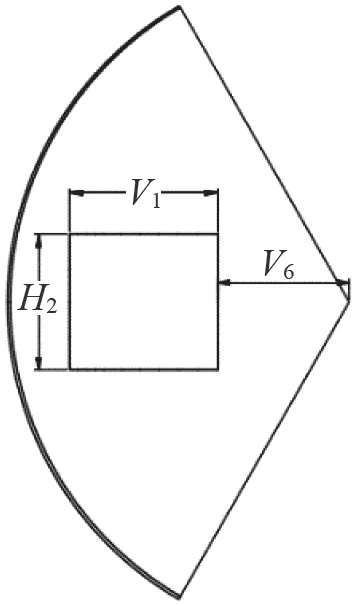
图5 优化变量Fig.5 Optimizing variables

模型：

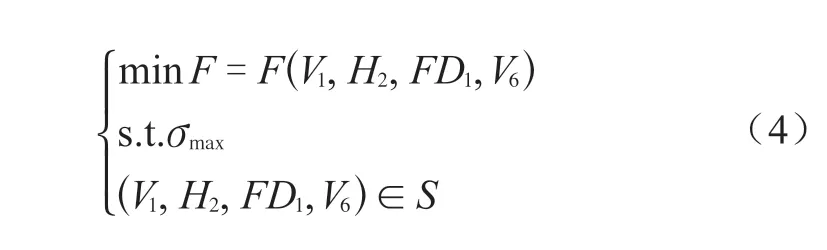
式中，目标函数F 是垫板质量最小，约束条件σmax为最大等效应力值，S 为设计变量的搜寻域。

3.2 设计变量设置

变量初值及搜寻范围见表3。

表3 垫板优化变量初值及搜寻范围Table 3 Initial value and search range of optimum variables for cushion plate mm

3.3 状态变量的设置

优化目标函数为垫板质量最小，约束条件见表4。

表4 垫板优化约束条件Table 4 Optimal constraint conditions of cushion plate

3. 4 优化算法选择

本文的优化设计运用的是ANSYS Workbench 中的Design Exploration 模块。Design Exploration 作为一种快速优化工具，实际上是通过设计点（可以增加）的参数来研究输出或导出参数的，由于设计点是有限的，因此也可以通过有限的设计点拟合成响应面（或线）来进行研究。

响应面法（RSM）对隐含的或需要花费大量时间确定的真实的功能函数或极限状态面，用一个容易处理的函数（称为响应面函数）或者曲面（称为响应面）替代，是一种基于插值或近似方法的代理模型方法。响应面法将复杂的输入输出函数简化为简单的数学方程，极大地减少了计算时间。

优化算法我们采用ANSYS Workbench 中的多目标遗传算法（MOGA），多目标遗传算法是模拟达尔文的遗传选择和自然淘汰的生物进化过程，处理的是一个种群，可搜索到Pareto 最优解集，通用性、鲁棒性好，且具有并行处理机制。ANSYS Workbench 采用的MOGA 是基于NSGAII 的一个变种，支持多目标和约束，适合计算全局最大值/最小值，可规避局部最优的陷阱。

3.5 支座优化结果

3.5.1 结构改进型优化结果

结构改进型只考虑垫板的位置变化，对垫板的尺寸不会进行改变，垫板的体积大小不会有较大的改变，所以目标函数不考虑垫板的质量，只考虑其最大等效应力。输入参数为V6——垫板距离封头中心点的距离，初始值为187 mm；输出参数为Equivalent Stress Maximum——最大等效应力，初始值为320.97 MPa。优化结果如图6 所示。

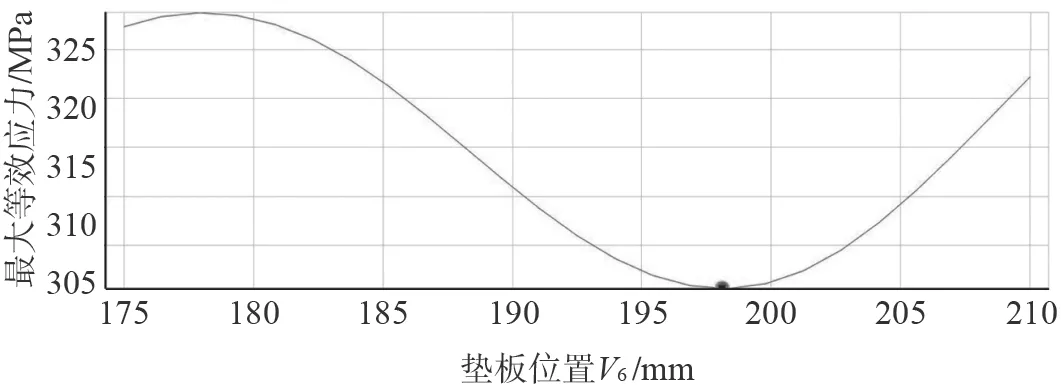
图6 垫板位置-最大等效应力拟合曲线Fig.6 Fitting curve of cushion plate position-maximum equivalent stress

表5 最小-最大值搜寻Table 5 Min-max search

由图6、表5 可知，当垫板距离封头中心点处198.1 mm 处时，最大等效应力值最小，数值为300.58 MPa，比初始值减少了20.39 MPa。采取有限元方法对优化结果进行校核，结果见表6。由表6可知，代理模型具有较高的精度。综上可知当垫板适当远离封头中心线位置，最大等效应力将会降低。

表6 代理模型精度Table 6 Proxy Model Accuracy

3.5.2 尺寸改进型优化结果

输入参数为V1—— 垫板长度，初始值为206 mm；H2——垫板宽度，初始值为190 mm；FD1——垫板厚度，初始值为8 mm。输出参数为Equivalent Stress Maximum——最大等效应力，初始值为320.97 MPa；Solid Mass——垫板质量，初始值为2.48 kg。优化结果如图7～图10 所示。

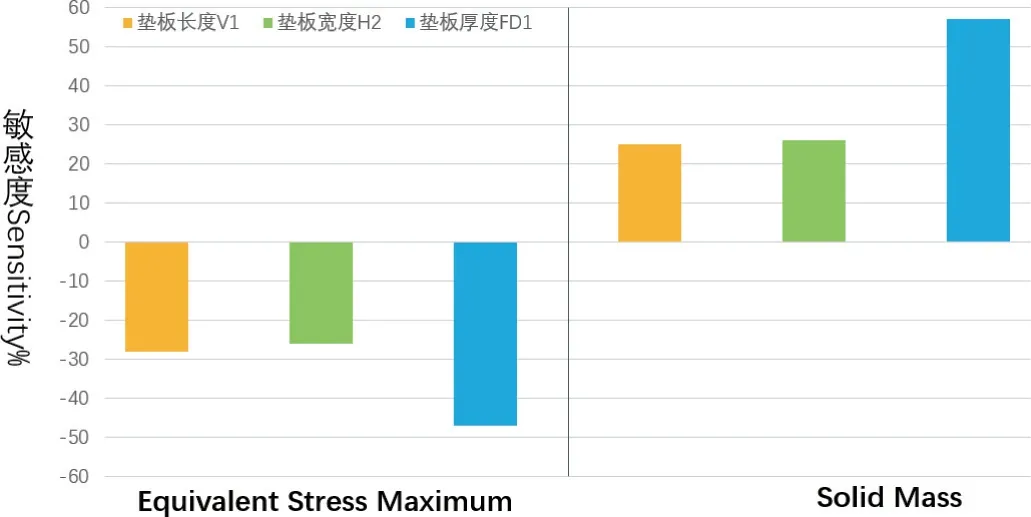
图7 参数敏感度分析Fig.7 Parametric sensitivity analysis

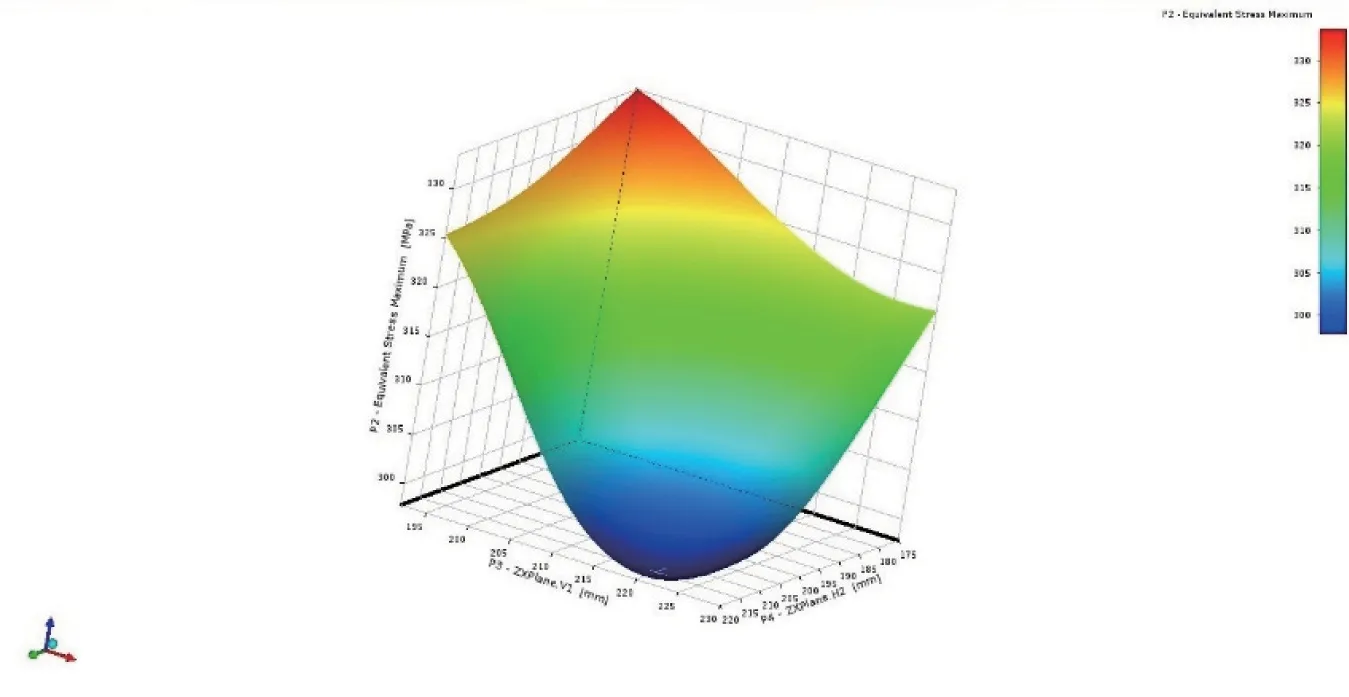
图8 V1、H2 对最大等效应力变化的应力分布图Fig.8 Stress distribution map of V1 and H2 for equivalent stress maximum change

图9 V1、H2 对质量的变化分布图Fig.9 Distribution chart of mass change of V1 and H2

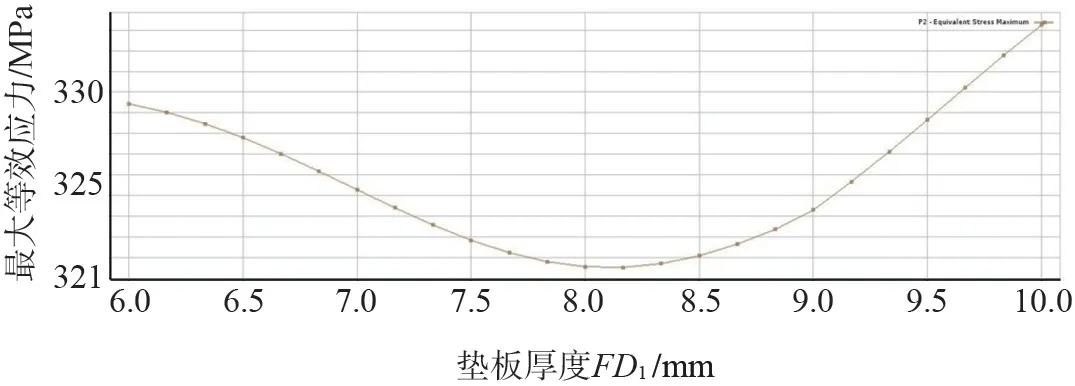
图10 垫板厚度-最大等效应力拟合曲线Fig.10 Fitting curve of cushion plate thickness-maximum equivalent stress

图7 是设计变量对于优化目标的敏感度结果，可以看出厚度对于垫板的应力以及质量影响较其他两个变量影响更大，长度及宽度对目标函数的影响大致相同。从图8 可以看出，最大等效应力随着垫板长、宽的变化，呈现出凹形变化，即两端应力值较大，中间应力值较低，当两个变量位于中间某一尺寸时，等效应力最小。图9 直观地表现出，垫板质量随着长度、宽度尺寸的增加而显著增长，同时结构的安全性也得到提高，但成本也相应的提高，所以在进行优化设计时需要综合考虑。从图10 中可以看出，最大等效应力值并不会随着厚度尺寸的增大而一直降低，相反，当厚度大于某一值时，最大等效应力值甚至会随着厚度的继续增加而相应地增大。对于这一现象出现的原因主要是因为封头的厚度只有4.5 mm，当与之接触的垫板厚度远大于封头厚度时，两者在容器承受载荷时，封头与垫板的受力变形将不协调，封头的厚度小，较容易变形，而垫板因为厚度大，不易变形，从而会使封头处的应力集中，导致最大等效应力值变大。

优化结果如表7 所示，根据优化得到的三组Pareto 解，选取重量最轻的那组解作为最终的优化结果，然后采取有限元方法对优化结果进行校核，结果见表8。由表8 可知，代理模型具有较高的精度。

表7 优化结果对比Table 7 Comparison of optimization results

表8 代理模型精度Table 8 Proxy model accuracy

经过以上的优化分析结果，当垫板长度V1为196.45 mm，宽度H2为181.5 mm，厚度FD1为5.025 6 mm 时，垫板质量Solid Mass 降至1.402 2 kg，最大等效应力值Equivalent Stress Maximum 为329.52 MPa。最大等效应力增大了2.66%，质量降低了43.46%。

3.5.3 结构与尺寸改进型结果

将垫板尺寸和位置同时作为优化变量，将最大等效应力和垫板质量作为目标函数，利用Design Exploration 进行优化设计，结果见图11、图12 和表9。

图11 参数敏感度分析Fig.11 Parametric sensitivity analysis

图12 V6、FD1 对最大等效应力变化的应力分布图Fig.12 Stress distribution map of V6 and FD1 for maximum equivalent stress change

由图11 可知，垫板的厚度对于其最大等效应力和质量相比较于另外三个变量影响更大。从图12 可以发现，最大等效应力随着垫板离封头中心点的距离V6和垫板厚度FD1的变化而呈现凹形变化，当距离V6以及厚度FD1处于中间某一值时，最大等效应力最小。

表9 优化结果对比Table 9 Comparison of optimization results

优化结果如表9 所示，根据优化得到的三组Pareto 解，选取重量最轻的那组解作为最终的优化结果，然后采取有限元方法对优化结果进行校核，结果见表10。由表10 可知，代理模型具有较高的精度。

表10 代理模型精度Table 10 Proxy model accuracy

经过以上的优化分析结果，当垫板长度V1为199.38 mm，宽度H2为175.67 mm，厚度FD1为5.003 8 mm，距离V6为190.77 mm 时，垫板质量Solid Mass降至1.378 4 kg，最大等效应力值Equivalent Stress Maximum 为328.0 MPa。最大等效应力增大了2.21%，质量降低了44.47%。

3.6 优化结果比较

前文已经通过计算得到了三种支座优化的方案，结果如表11 所示。

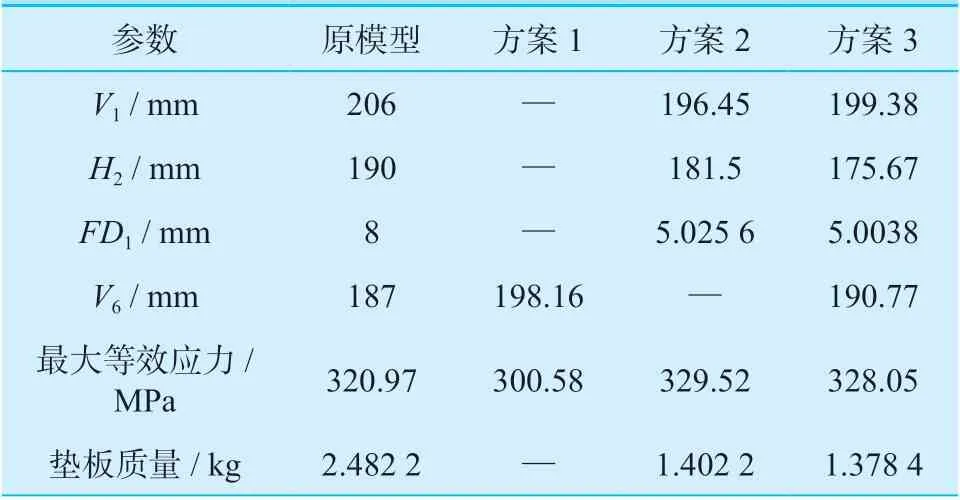
表11 三种优化结果Table 11 Three optimization results

从表11 可以看出，方案1 中将垫板位置V6远离封头中心点时，最大等效应力将会降低；方案2 中适当地减小垫板的长宽和厚度尺寸，虽然最大等效应力值会上升2.66%，但垫板质量将会降低43.46%；方案3 同时考虑了垫板的尺寸以及位置参数，最大等效应力增大了2.21%，质量降低了44.47%，得出的优化结果也是最好的。