边坡可靠度的Bayes估计及后验稳健性

夏增选，李 萍，曹 博，李同录，沈 伟，康海伟

(1.长安大学地质工程与测绘学院，陕西 西安 710054;2.黄土高原水循环与地质环境教育部野外科学观测研究站，甘肃 正宁 745399)

我国黄土滑坡隐患点较多，近年来黄土滑坡灾害屡有发生，造成了大量生命财产损失。由于黄土滑坡多为边坡失稳滑动形成，因此研究黄土边坡稳定性，是防治黄土滑坡的关键问题，也一直是工程地质界研究的重点课题[1-4]。传统的边坡稳定性研究方法主要有刚体极限平衡法与数值分析法，应用这些理论计算的稳定系数为一定值。然而，黄土边坡稳定性受多种不确定因素影响，比如：土体参数空间变异性、分析模型的误差、破坏模式的差异等。因此，采用传统确定性的分析方法评价边坡稳定性，计算结果存在较大的不确定性。采用稳定性指标的概率分布取代单一定值，更加符合实际。

岩土工程师在处理复杂工程地质问题时，并非严格按照试验室或原位测试的岩土体参数测试结果，进行边坡稳定性评价及治理，而是根据工程经验进行参数调整，使计算结果更加符合实际。Bayes理论多用于减小岩土体参数及模型不确定性对边坡稳定性的影响，并合理地将工程经验或专家信息纳入理论框架。由于Bayes理论具有公式物理意义明确，形式简洁的优点，其在多个领域得到了广泛应用[5-10]。当根据数据进行统计推断时，描述数据的模型存在敏感性，如果数据很多，这种敏感性变得很小，这种性质称之为稳健性[11]。在Bayes统计推断中，稳健性亦是重要问题。当先验分布发生小幅度改变时，后验分布是否会发生较大的改变，Box等[11]称之为推断稳健性问题。应用Bayes理论进行统计推断时，为建立先验分布或似然函数，多数学者根据经验对先验或总体分布的概型进行假设[12-15]。然而，先验分布的表达并不是唯一的，不同的先验分布会得到不同的Bayes推断结果。因此，有必要研究先验分布的不确定性对后验结果的影响。Bayes后验稳健性分析方法主要有：边缘分布分析法[9,16]、后验期望损失分析法[17-18]。后验稳健性分析应用在边坡稳定性研究中的成果鲜有报道。

本文将衡量边坡稳定性的3个指标(稳定系数、可靠指标和失效概率)视为随机变量，通过Bayes理论将研究区内同类型的边坡作为先验信息。同时，将边坡自身的稳定性参数作为样本信息。Bayes理论集中了边坡稳定性参数总体、样本和先验信息后，对于先验分布的更新，得到了更加合理、更加符合实际的稳定性评价结果。加之，为了研究先验分布的不确定性对后验稳定性结果的影响，对后验结果进行了稳健性分析，从而保证了后验结果的准确性。

1 Bayes 理 论

1.1 Bayes公式

Bayes理论将未知参数θ视为随机变量，采用概率分布描述随机变量θ。Bayes公式的概率密度函数形式表述如下：

(1)

式中：x——样本值；Θ——参数空间；π(θ)——θ的先验概率密度函数；p(x|θ)——在样本x给定下θ的概率，即似然函数；f(θ|x)——θ的后验概率密度函数。

1.2 正态后验分布

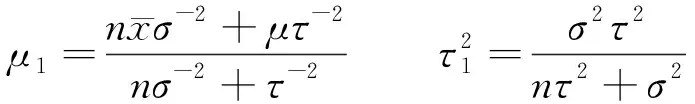
(2)

1.3 后验稳健性分析方法

在Bayes推断中，如果实际应用条件与假设条件不完全相同，统计分析的优良性难以继续保持，因此必须分析由于条件差异而引起的后果[9]。一般通过历史经验或专家总结获得未知参数的先验分布，但是先验分布存在不同的概型，且存在较大的人为主观性，先验分布的不确定性直接影响后验分布的结果。因此，有必要研究当先验分布发生波动时，后验分布是否会有大的改变，即后验分布的稳健性问题。

假设Г为先验分布族，a为Bayes统计推断中所采取的行为(策略)，L(θ,a)为行为(策略)a的损失函数，记ρ(f(θ|x),a)为行为(策略)a的后验期望损失(损失函数L(θ,a)对后验分布f(θ|x)的期望)，当先验分布π在先验分布族Г中变动时，则式(3)表示可能的后验期望损失范围，进而评价行为(策略)a的稳健性。

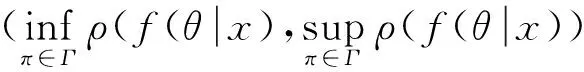
(3)

式中：inf——下确界；sup——上确界。

在Bayes决策行为中选择一可信集C(C∈Θ)，后验期望损失函数为

(4)

(5)

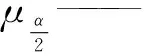
采用先验分布的ε代换法构成先验分布族Г：

Γ={π:π=(1-ε)π0+εq,q∈D}

(6)

式中：π0——初始先验分布；ε——代换系数，0<ε<1；q——代换分布；D——代换分布族。

后验期望损失可由下式计算：

(7)

式中：C——采用π0确定的最大后验密度(HPD)可信集。

2 工程实例分析

2.1 边坡计算模型与参数选取

现以西安咸阳国际机场污水排放口黄土边坡为例，说明Bayes理论在边坡稳定性计算结果分析中的具体应用。该边坡位于泾阳县高庄镇傅家村黄土台塬北缘，台塬与泾河大致平行。西安咸阳国际机场污水排放系统经台塬至泾河高漫滩，污水经净化流入泾河。该边坡所在研究区如图1所示。排水系统穿越的边坡地形破碎，在边坡体周壁小滑塌、小崩塌大量分布，两侧数百米处各有一大型滑坡。在边坡顶部发现拉裂缝，近东西向展布，呈锯齿状延伸[19]。据李萍等[20]对极限状态坡的定义及判别标志，该坡为典型的黄土极限状态自然坡。

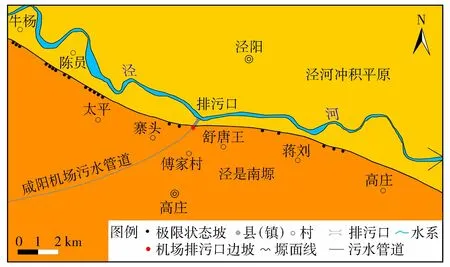
图1 西安咸阳国际机场污水排放口边坡研究区域Fig.1 Study area of a loess slope at the sewage outlet of the Xi’an Xianyang International Airport

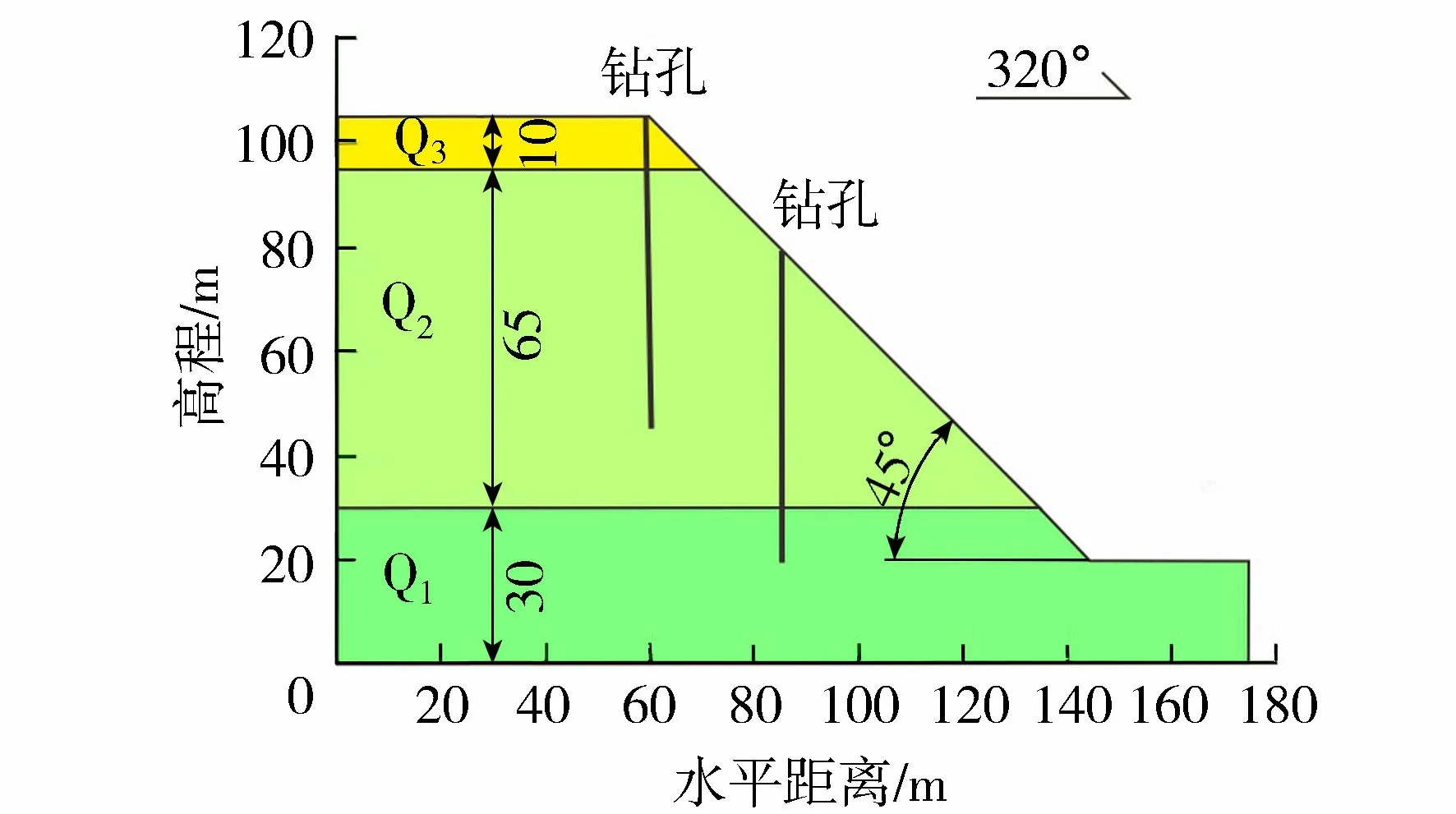
图2 边坡分析模型(单位:m)Fig.2 Model diagram of slope analysis(units:m)

边坡高85 m，坡向320°，坡度40°～50°，最陡处可达65°。坡顶为黄土台塬，坡底为河漫滩。黄土台塬地层主要为第四系风积黄土，夹十余层古土壤，L1-S9层黄土-古土壤序列从坡顶至坡底清晰可见，下伏河流冲积相的致密黏土。具体地层上部为约10 m厚晚更新统黄土(Q3)，中部为约65 m厚中更新统黄土(Q2)，底部为10 m厚早更新统黄土(Q1)。

本文采用Geo-slope/w建立边坡模型，如图2所示。该模型采用坡高85 m，坡度45°。在坡体上沿边坡横向依次纵向(320°)布3条测线，每条测线上布2个钻孔，每条测线上的2个钻孔试样的物理力学性质测试结果组成一个样本数据，模型计算所需土性参数见表1。研究表明，不同地层的黄土抗剪强度参数多服从正态分布[1]，且正态分布的概率分析形式较为简单，应用最为广泛，因此，该边坡模型抗剪强度参数采用正态分布。

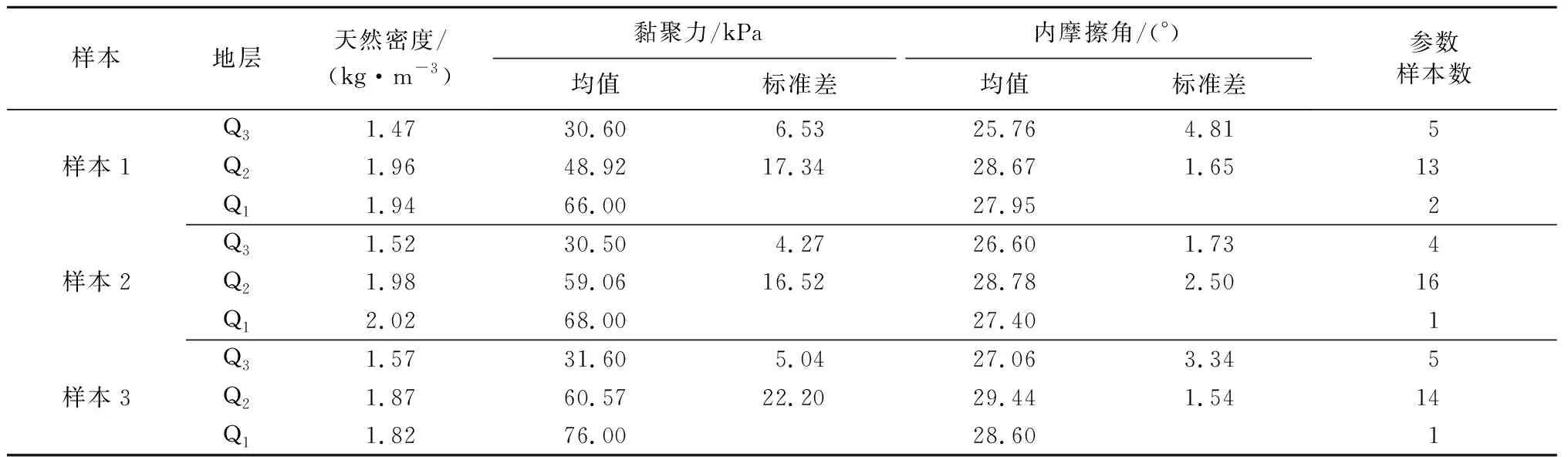
表1 边坡土性参数Table 1 Soil parameters of slope

2.2 边坡稳定性参数计算

采用表1中所列边坡土性参数，应用Morgenstern-Price(M-P)法与Monte-Carlo法对边坡稳定性进行可靠度计算，指定了边坡滑面剪入和剪出区域，计算结果(稳定系数Fs、可靠指标β和失效概率Pf)作为样本信息，采用样本土性参数边坡可靠度计算结果如图3所示。

表2 先验边坡信息Table 2 Prior slope information

2.3 先验概率密度函数建立

以泾阳南塬为研究区(图1)，研究区地貌为黄土台塬，出露第四系地层，地层呈水平状沉积，厚度变化小。采用李萍等[20]的极限状态坡鉴别标准，现场量测研究区内21个自然条件下的极限状态坡，21个极限状态坡与研究边坡位于同一研究区域，同时均属于黄土极限状态自然坡。21个先验边坡位置见图1，坡高和坡度见表2。表2中所列极限状态坡与排污口边坡的土层沉积特征一致，故仍采用图2所示地层厚度。各地层的土性参数采用工程经验值，并参考李萍等[21]对该区域土性参数的统计结果，土性参数值见表3。李萍等[2]认为黄土地区黏聚力服从对数正态分布、内摩擦角服从正态分布，先验边坡稳定性计算加入此“专家信息”，计算结果见表2。将计算所得21个边坡的稳定系数、可靠指标及失效概率进行统计，作为机场污水排放口边坡的先验信息。

表3 先验边坡土性参数Table 3 Soil parameters of prior slopes

将表3中的稳定系数、可靠指标及失效概率绘制频率直方图，在直方图上进行正态分布拟合，如图4所示，并对其分别进行K-S检验，在显著性水平为0.05下，统计显著性依次为0.11、0.08和0.10，统计显著性均大于显著性水平，结果表明，三者均服从正态分布。

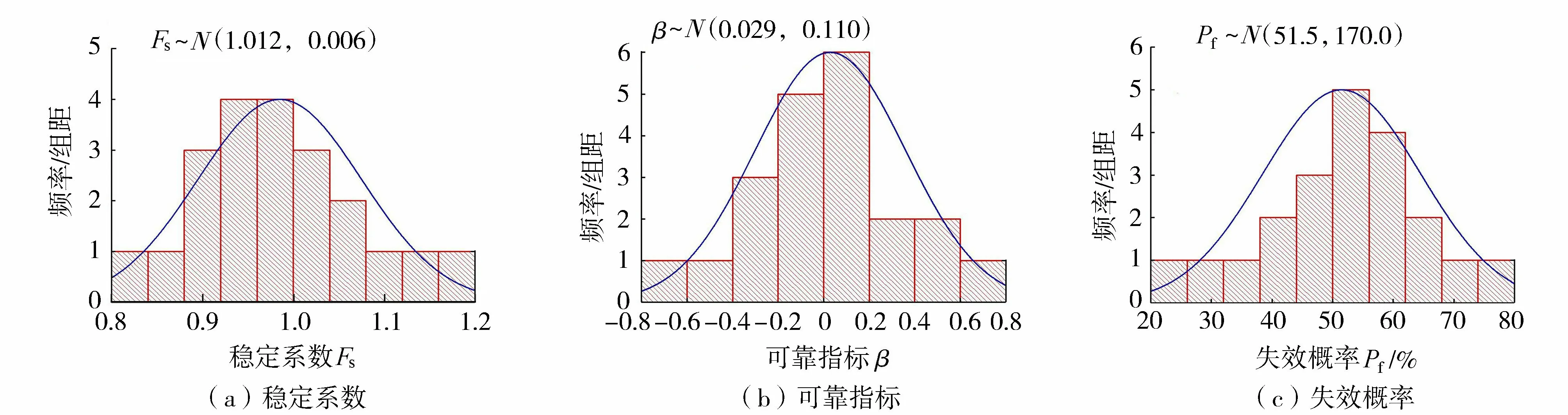
图4 边坡稳定性参数频率直方图Fig.4 Frequency distribution histograms of slope stability parameters

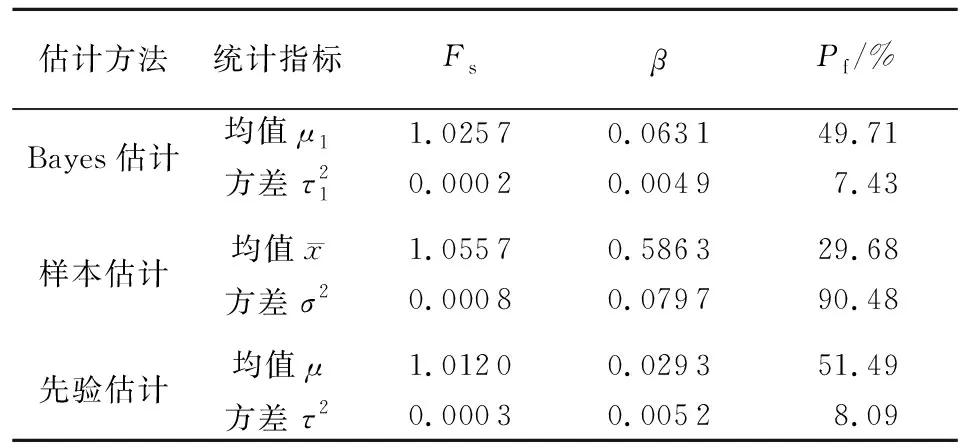
表4 Bayes估计与样本和先验估计结果对比Table 4 Comparison of Bayesian estimation, sample and prior estimation

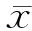
2.4 后验概率密度函数计算

采用样本方差估计总体方差，在总体方差已估计的前提下，将表4的正态先验和样本相关参数代入式(2)，可得边坡稳定性参数均值后验分布，并将Bayes估计结果与样本和先验估计结果进行比较,见表4。

Bayes估计与样本和先验估计结果对比表明，边坡稳定性参数均值的Bayes估计介于样本估计与先验估计之间，估计结果得到了很好的修正。方差代表了估计结果的精度，Bayes估计的方差比样本估计和先验估计结果均小，Bayes估计结果的精度为先验信息与样本信息精度之和。同时，研究边坡后缘有拉裂缝，表现为更接近破坏的状态，研究边坡样本估计失效概率为29.68%，与研究边坡的野外特征并不完全相符。而加入先验分布后，失效概率为49.71%，与研究边坡的野外特征更贴切。

2.5 后验分布稳健性分析

机场污水排放口边坡稳定性的Bayes推断中，假设了稳定系数、可靠指标和失效概率的先验分布均服从正态分布，并对其进行了检验，详见2.3节。但是，先验分布服从的概型并不唯一，概型参数会随统计数据的多少而发生改变，并且先验分布考虑专家信息或工程经验，人为主观性较大，因此，先验分布存在较大的不确定性。假定代换分布q服从均匀分布，即代换分布族为均匀分布族，表达式为

D={q:q=U(μ-k,μ+k),k>0}

(8)

式中：k——均匀分布族区间系数，上限根据边坡工程实际情况而定。

假定先验分布存在5%、10%和15%的改变，即代换系数ε分别为5%、10%和15%。在边坡工程中，稳定系数均值理论最小值趋于0，同时，由图4可知，稳定系数初始先验分布均值趋于1，区间系数k上限为1，同理可得可靠指标、失效概率的区间系数k上限分别为1、50%。经计算得边坡稳定性指标后验稳健性结果，如图5所示。结果表明：(a)稳定系数、可靠指标及失效概率均值后验期望损失，随着分布区间系数k的增大而波动，并且随着代换系数ε的增大，后验期望损失依次增大；(b)稳定系数均值后验期望损失开始有所波动，随后较快趋于较小的后验期望损失值，且后验期望损失上限较小，稳健性良好；(c)可靠指标和失效概率均值后验期望损失一直处于波动状态，但波动的最大后验期望损失都在20%以内。将稳健性划分为4个等级，即最大后验期望损失在5%以内代表稳健性很好，10%以内代表稳健性好，20%以内代表稳健性较好，20%以上代表稳健性差，因此可靠指标和失效概率的稳健性较好。可见，先验分布的正态概型是合理的，先验分布的不确定性对后验结果并未产生较大影响。

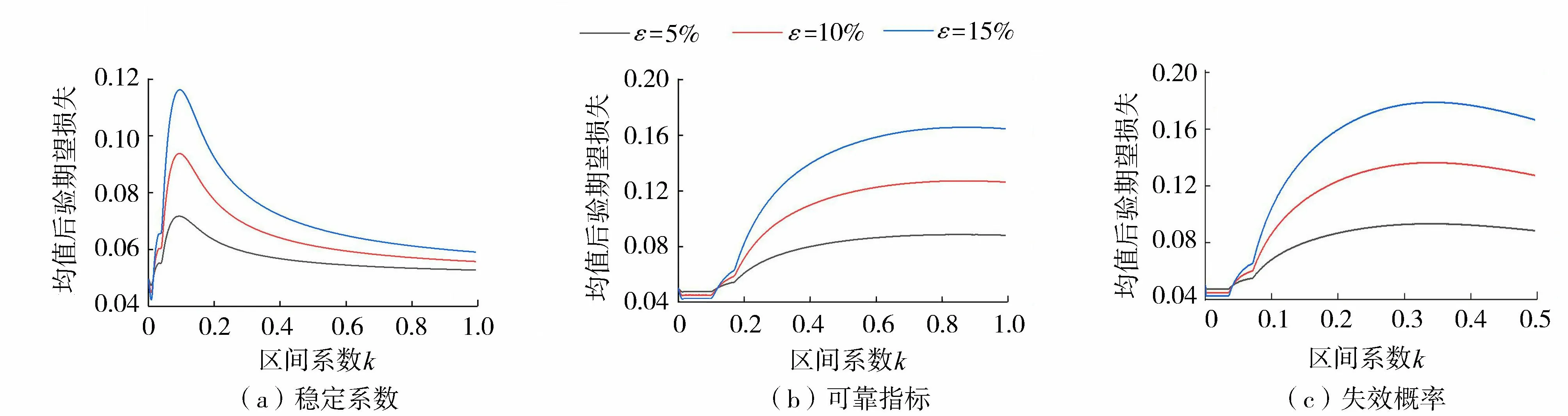
图5 边坡稳定性指标均值后验期望损失Fig.5 Posterior expected loss of slope stability index means

3 结 论

a. 采用Morgenstern-Price法与Monte-Carlo法对研究区内的极限状态黄土自然坡的稳定性进行可靠度计算。对稳定系数、可靠指标及失效概率进行频率直方图统计与正态分布拟合及检验，结果显示，极限状态坡稳定性指标均较好地服从正态分布。

b. 对黄土边坡稳定性计算结果进行了Bayes分析。以泾阳南塬机场污水排放口边坡为例，以研究区21个极限状态坡建立先验分布，以边坡自身稳定性参数作为样本信息，计算了稳定系数、可靠指标和失效概率均值后验分布，并将Bayes计算结果与样本估计和先验估计进行了比较，Bayes计算结果极大地降低了不确定性，结果更为精确，更加符合实际。

c. 鉴于先验分布的类型与分布参数并不唯一，且随统计数据的多少和专家经验发生改变，本文通过ε代换法构建先验分布族，以后验期望损失范围评价后验结果的稳健性。当代换系数ε为5%、10%和15%时，稳定系数均值后验期望损失较快趋于较小值，可靠指标和失效概率均值后验期望损失一直在20%损失范围内波动。结果表明，构建的先验分布合理，后验结果稳健性较好，Bayes估计结果更加准确。