基于改进模糊层次分析法的二次设备差异化改造方案评价

崔 玉，朱东升，胡潇月，周 玲，黄帅飞，崔建双

(1.国网江苏省电力有限公司, 江苏 南京 210024； 2.中国能源建设集团江苏省电力设计院有限公司，江苏 南京 211102；3.河海大学能源与电气学院，江苏 南京 211100)

智能电网作为当前电力系统发展的重心，配套的智能变电站数量不断增加[1]。“十三五”规划期间(2016—2020年)，国家电网公司持续推进智能变电站建设和传统变电站的改造升级工作。伴随着变电站建设的进行，大量变电站接近或超过寿命预期，受制于变电站保护和测控等二次设备(通称二次设备)种类众多，不同电压等级、不同二次设备对电网的重要程度不尽相同，且存在技术改造资金有限、二次班组承载力和停电风险等因素的影响，需要对整屏更换、整机更换、插件更换3种技术改造升级方案进行评估分析。应重点从停电风险、改造工期、人力要求、资金要求等方面进行各类方案的比较，分析明确不同变电站选择改造方案的原则，形成系统的差异化技术改造评价理论。

除了易损件与电源模块可以根据维护计划定期更换外，传统主流的二次设备运行维护与改造均是按计划进行和面向故障处理的“一刀切”方案，即通过更换屏柜(含柜内装置及端子排)及屏柜相关对外接线实现二次设备的改造。这种方式改造全面，但存在项目周期长、工程量大、用工用时较多和电网运行风险高等缺点。现在可以选择的还有整机更换和插件更换的改造方式。整机更换指将原有柜内设备进行整装置更换。插件更换指对原有装置全部插件进行更换的改造方案，不影响装置对外接口和屏柜内外端子排接线。何时采取何种改造方案，至今没有成熟通用的标准和理论依据。

二次设备改造方案评估具有模糊性的特点[2]，是一个多准则决策问题(multi-criteria decision-making，MCDM)，可采用集合专家经验和知识的专家判断法[3]，如层次分析法(analytic hierarchy process, AHP)[4]、德尔菲法(Delphi method)或组合赋权法[5]来评估二次设备改造方案。其中，AHP适用于评价多个具有相同属性的评价对象来获得最佳决策方案，具有系统、灵活和简洁的优点。同时，随着研究的深入发现模糊集理论能够更好地处理MCDM评估过程中存在界定不清的模糊性和统计信息残缺问题。将其和层次分析法这种多属性决策方法相结合为模糊层次分析法[6]，可以将各个问题在层次化的基础上对评价目标的各种决策因素进行定性定量分析。刘鑫等[7]将AHP与模糊综合评价法相结合，通过实例工程验证了实用性和可靠性，但工程实践时一致性检验步骤繁琐，不利于实施；张尚等[8]突出了犹豫属性的存在，提出直觉模糊层次分析法，并用以评估电网运行状态，保证了方法的灵活性，但存在定义的分函数不够全面的问题。为使指标权值求取过程准确反映标度的模糊性和不确定性，多维度传达专家评估的知识经验与立场，有研究人员引入三角直觉模糊数改进模糊层次分析法中判断矩阵元素的不确定性表达方式[9-10]，进而保留有效信息，降低主观因素的影响，形成三角直觉模糊层次分析法(triangular intuitionist fuzzy analytic hierarchy process, TIFAHP)。

本文从变电站的角度，对变电站二次设备技术升级改造可选的改造方案进行评估。通过对变电站的运行维护记录和设备技术改造的经验进行分析，选取二次设备改造后寿命、改造耗费、管控级别、运行环境和二次回路健康水平共5个评价指标。在参考多种评估决策模型的基础上使用三角模糊数描述专家评估内容，结合模糊层次分析法确定各指标的相对权重，最终确定变电站应采取改造方案的优劣排序，为精准的二次设备差异化技术改造提供理论支撑。结合具体案例验证了本文评估模型的有效性。

1 二次设备技术改造方案评估指标

为准确描述电力二次设备的劣化程度，对Q-GDW 11285—2014《继电保护状态评价导则》[11]评估标准和DL/T587—2016《继电保护和安全自动装置运行管理规程》[12]进行详细分析，结合电力电子元器件特性和实际工程应用经验，对预防性试验、带电检测和在线监测分值评价原则进行提炼[13-14]，得到如下包含具体二级指标的五维考核指标。

1.1 二次设备改造后寿命

二次设备的故障概率是影响二次设备物质寿命的关键因素，对整机和整屏2种改造方式来说，故障概率又由其组成插件的集合决定[15]。二次设备故障后会进行保护闭锁不再动作或行使保护功能，在这里认为是仅有“故障”和“正常”的二元状态模型。插件故障导致二次设备故障的故障率和时间关系表示为

(1)

式中：t——设备投入运行时间；f1(t)——插件故障概率；f(t)——服从Weibull分布的概率密度函数；λ、β——调整系数，β<1、β=1、β>1分别对应浴盆曲线时序的3个阶段。

整机或整屏由插件板卡组合而成，整体故障概率受组成部件的故障率影响。

(2)

式中：f2(t)——整机或整屏故障概率；p——组成整机或整屏的插件数目；q——每种插件的数量。

从1台二次设备投入运行开始，组成二次设备的所有插件的故障概率开始增加(不记出厂老化测试的浴盆曲线第一阶段)。进行插件更换后仅当前插件故障概率复位，可使设备故障率相比于故障前有所下降；进行整机更换后，包含多个插件的整机故障概率复位，使设备故障率相比于故障前有较大下降；进行整屏更换后，全部插件故障概率复位，也就是更新设备，并重新计算设备的故障率。

单一插件故障改造后的故障变化趋势如图1所示，采用3种改造方式对故障概率趋势影响的对比结果如图2所示。图2中treform表示对设备进行改造的时间，tout表示设备退出运行的时间，tout1、tout2、tout3分别表示整屏更换、插件更换、整机更换时设备退出运行的时间。

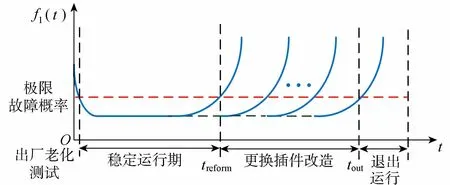
图1 单一插件故障改造后故障概率趋势Fig.1 Failure probability trend after reconstruction of single fault

图2 3种改造方式对故障概率趋势的影响Fig.2 Effect of three transformation methods on failure probability

1.2 二次设备改造耗费

改造方案的不同决定了运行周期内其寿命和故障次数的不同，进而影响整个运行周期内的耗费值[16]。

CFD=(aTMTTR+bCSE+cCL)NF

(3)

式中：CFD——元件改造耗费；TMTTR——停运改造时长；CSE——被改造设备价格；CL——人力物力花费；NF——退出运行前进行改造的次数；a、b、c——调节权重。

1.3 二次设备管控级别

二次设备的管控级别由设备重要程度决定，可以按照不同电压等级与其故障时造成影响的程度进行区分[17]。

I=kP(t)V

(4)

式中：I——设备重要程度指标；k——故障影响系数，即当前故障后造成的停电负荷量占变电站总负荷量的百分比；P(t)——设备的故障概率；V——电压等级量化值，取值可按500 kV及以上取1,220 kV取220/500,110 kV取110/500,110 kV以下取35/500。

1.4 二次设备运行环境

二次设备含大量的电子元器件，受所处环境因素影响，即受温度、湿度、电磁干扰、管理规范程度等环境应力的作用。设计、运行时综合考虑这些因素，有利于延长装置寿命。可以参考Q/GDW 11285—2014《继电保护状态评价导则》[11]中的运行环境评分规则，进行设备环境状态评估，在此不再赘述。

当设备因温湿度、电磁干扰和管理不规范导致过热、受磁和积尘进水等状况时，会使二次设备整体的故障概率上升，二次设备屏柜及电缆寿命下降，建议按整屏更换、整机更换、插件更换的先后顺序进行。

1.5 二次回路健康水平

二次回路健康水平由二次电缆寿命和二次回路接线水平决定。其中电缆的寿命用L这一非负随机变量来表示[18]：

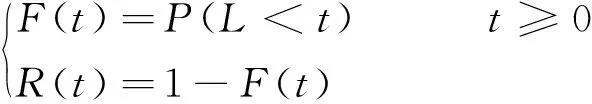
(5)

式中:F(t)——二次电缆运行的故障概率；R(t)——t的可靠度函数，电缆的可靠寿命是指在给定可靠度情况下所对应的时间，记作t(R)。一般情况下，可靠性随着时间的增长而降低，即t(R)=R-1(t),R-1(t)为R(t)的反函数。

二次回路接线水平，主要包括按图施工、接头牢靠、标号规范与配线规范整洁等要求的落实情况。二次电缆寿命对二次设备改造的方案选择影响巨大，改造时涉及繁重的接线铺埋工作，费工费时，当不满足可靠性要求时应采用整屏更换的改造方式。

2 二次设备差异化改造方案评估模型

将以上所提各类评价指标基于层次分析法理念进行层次化处理。针对二次设备改造方案的选择进行评估，将差异化改造方案评估问题分为目标层、准则层和方案层。目标层为二次设备差异化改造方案选择，准则层为二次设备的改造后寿命、改造耗费、管控级别、运行环境和二次回路健康水平5个指标，方案层为插件改造、整机改造和整屏改造3种，由此建立二次设备差异化改造方案选择影响因素模型(图3)。

层次分析法原理为同层元素相比较得出相对上层元素的重要程度排序，本文中为准则层5个指标比较得出相对目标层的重要程度；对准则层每个因素来说，方案层的3个方案相比较得出相对准则层改造方法的优先性排序；同时，对准则层来说还有自己对应的准则子层排序。

2.1 三角直觉模糊理论

为处理不能准确量化和不同属性的指标，在应用层次分析法理论对两元素相对重要性评价时，首次引入三角直觉模糊数，完成对层次分析法的改进。直觉模糊集同时考虑隶属度、非隶属度和犹豫度3个方面的信息[19]，通过简要介绍三角直觉模糊理论来说明对层次分析法标度的改进原理。

2.1.1 三角直觉模糊数的定义

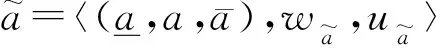
2.1.2 三角直觉模糊数的截集

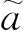
(6)

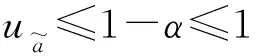
(7)

2.2 改进三角直觉模糊数排序方法

评价过程中需要借助截集思想计算矩阵中元素的综合值，以比较三角直觉模糊数大小。借鉴Choquet积分集结算子的思想[20]，同时，考虑截集的权重函数α得到新的得分函数。

(8)

2.3 改进直觉模糊层次分析法评估模型

在应用传统AHP时采用三角直觉模糊数将模糊判断矩阵传统9标度相对评价值模糊化,避免信息丢失[21]。同时，在确定权重时采用层次分析法的相对权重原理，避免了求取指标权重时反复的迭代和修正。通过创新形成的TIFAHP法，在处理二次设备改造方案评估等多属性、非可加指标时有较好的实用性,其应用步骤如下：评价主体对被评目标A可选的m个方案Pi(i=1,2,…,m)进行评估，以求出当前最适合采用的改造方案。可设基于上层关系的本层n个指标集合为U={u1,u2,…,un},来自不同机构的s名专家Ek(k=1,2,…,s)组成评价小组。

构建TIFAHP评估模型的求解步骤如下：

a. 形成方案评估的层次结构模型。根据图3，通过计算每个元素的三角直觉模糊数的综合值大小，按层求取各层元素的相对权重并逐层加权递推，元素间相互比较采用三角直觉模糊数进行。

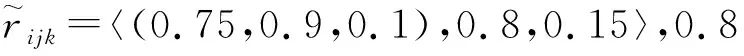
(9)

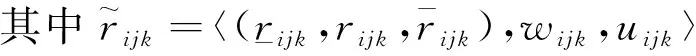
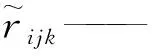
c. 判断矩阵规范化。对三角直觉模糊决策矩阵去量纲规范化。

对于成本型属性

(10)

对于效益型

(11)

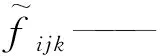
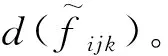
那么指标集U中当前层各元素的得分排序：

Wk={d(u1k),d(u2k),…,d(unk)}

(12)

采用行和归一化处理：

(13)

处理可得层元素的综合得分排序：

(14)

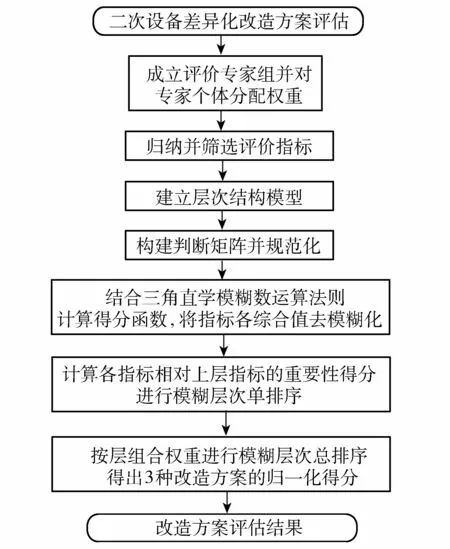
图4 二次设备差异化改造方案评估流程Fig.4 Flow chart for evaluation of differential transformation scheme of secondary equipment

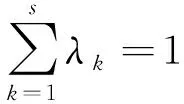
(15)

按层递归权重得到模糊层次总权重排序：

(16)

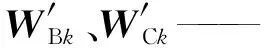
由以上步骤得到基于TIFAHP 的二次设备改造方案评估流程(图4)。

3 案 例 分 析

3.1 模型验证方法

对江苏某220 kV变电站开展二次设备差异化改造。首先，根据该变电站存在的问题和需求选取层次分析目标问题中所包含的要素，归纳具有支配逻辑关系的元素并将其层次化，进而构建差异化改造方案评价的层次模型；其次，成立三人评价专家组(分别来自变电站业主、二次设备厂家和设计院)，专家赋权分别为0.4、0.3、0.3；最后，按第2节步骤对改造方案进行评估。为简化表述，仅给出准则层各因素间的权重向量求取过程，二级指标和方案层对准则层元素的求值定权步骤相同。

3.2 构建三角直觉模糊判断矩阵

根据图3所示层次结构，由专家组按照自身经验和第1节关联目标层的各准则层构成因素进行评价打分，形成单层模糊判断矩阵RA-B，见表1。

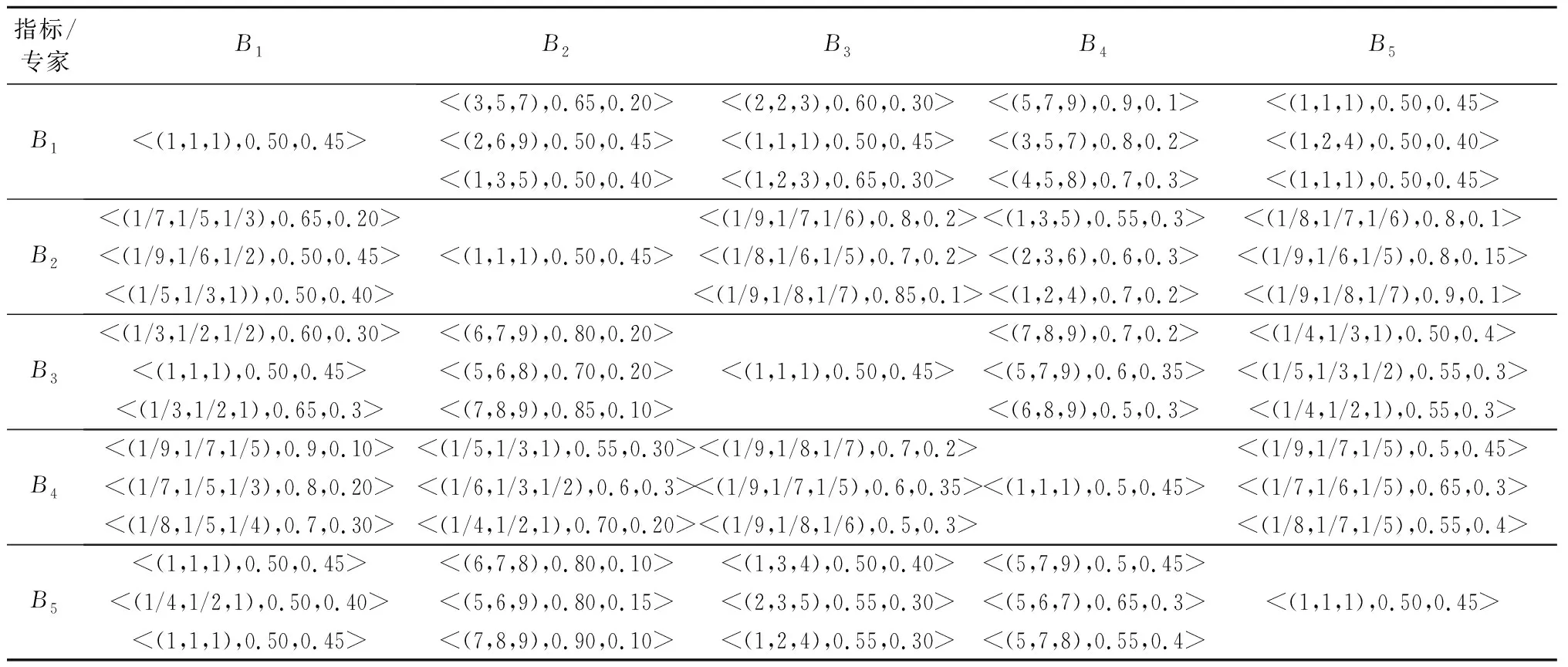
表1 单层三角直觉模糊判断矩阵RA-BTable 1 Judgment matrix RA-B of single layer triangular intuitionistic fuzzy

对表1按式(10)～(11)进行处理得到规范化的模糊判断矩阵FA-B，计算得分函数转化为传统AHP计算并应用式(13)～(15)处理得到准则层到目标层的权重得分排序。

(17)

同理可得方案层到准则层各判断矩阵RB-Ci,i=1，2，…，5的单层综合模糊权重。

3.3 计算差异化改造方案评估排序结果

组合各层的模糊权重得到全局的综合模糊权重(方案层相对权重C1、C2、C3分别为0.213、0.432、0.355)，将其和传统模糊层次分析法结果对比(方案层相对权重C1、C2、C3分别为0.27、0.43、0.30)，可知前者区分度明显好于传统模糊层次分析法。

3.4 改造方案综合评价结果分析

通过对该变电站进行流程评估，根据方案层权重结果，得出应优先考虑采用整机更换的改造方式。对于该变电站来说，设备投入运行较久，插件改造需要改造较多的插件，用工、用时、造价的耗费高于整机改造已经不再满足本案例的经济型要求，不予考虑。同时根据评估结果，屏柜及部分二次回路状态良好，无需采用长工期、高耗费的整屏更换方式。整机改造不仅节省技术改造资金，提高项目投资精准化水平，而且可降低二次班组承载压力、保障电网运行的可靠性。

4 结 语

本文提出变电站二次设备差异化技术改造理念，确定二次设备差异化改造参考评价指标，并给出评价标准和计算方法；改进加权打分评价法，避免了趋同性，应用易操性强的三角直觉模糊数进行评价判断，使改造方案排序结果区分度明显；对实际变电站进行改造方案进行了评价验证。

本文建立的按需灵活选取整屏改造、整机改造和插件改造的评估模型，可为变电站技术改造方案的选取提供参考，降低了业主配合时间，提升了人员的劳动生产率，为就地化保护的应用推广打下运行维护检修基础。下一步应纳入变电站寿命周期内二次设备的全寿命周期成本，精确评估二次设备寿命，实现长时间尺度的二次设备改造计划，形成改造计划安排表，方便二次设备的统一管理和采购，提高电网关键设备的维护保障和管理能力。