毛细管法测量流体黏度理论分析*

刘战果 庞学霞 常晗硕 李常伟 赵志岗 段超予

(河北大学物理科学与技术学院 河北 保定 071002)

1 引言

黏性是流体的固有物理属性.流体流动时会在相邻流体层之间产生内摩擦力，此即流体的黏滞(性)力，亦称黏滞阻力.流体的黏度(又称黏滞系数)是描述流体内摩擦力性质的重要物理量，能够表征流体反抗形变的能力.流体分子间的引力和分子热运动是形成黏性的原因.

流体黏度的测量方法有落球(针)法、毛细管法、转筒法等，其中毛细管法适用于测量黏度较小的液体，例如水、酒精或者血液.毛细管法测量流体黏度是基于流体力学领域的泊肃叶公式，实际上，基于这种理论测量流体黏度进行了不同程度的近似[1～6].本工作针对毛细管法测量流体黏度的一种简易装置，分析了基于不同理论的误差，其结果可以为任课教师讲授实验理论提供参考素材，也可以为学生在实验的过程中应用已学知识分析问题、解决问题提供参考.

2 黏度的定义及毛细管法测量黏度的简单装置

流体中两个移动边界之间的摩擦导致了流体剪切，描述这种层流剪切行为强度的物理量叫做流体的黏度或剪切黏度.黏滞力是流体受到剪切应力变形或拉伸应力时所产生的阻力.在一般的平行流动(即层流状态)中，剪切应力τ正比于速度u在垂直于流动方向的y′轴的梯度[1]，即

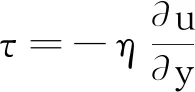
(1)

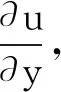
毛细管法是依据该黏度定义且能最容易实现测量流体(只适用于低黏度流体)黏度的方法之一，图1给出了一种毛细管法最简单的实验装置设计.

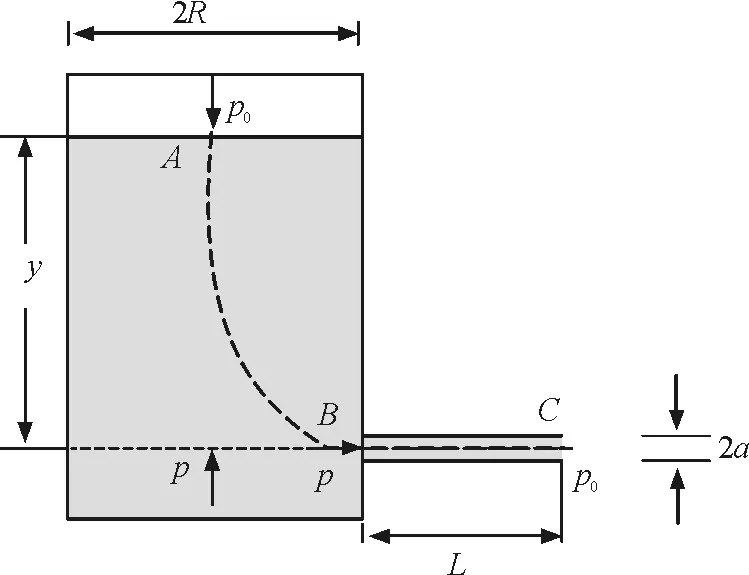
图1 毛细管法测量流体黏度实验装置示意图

如图1所示，圆柱形蓄水桶内直径为2R，蓄水桶靠近底端处是一个长度为L、直径为2a的毛细管，整套装置处于大气压p0下.蓄水桶中盛有低黏度液体，液面到毛细管中心线的距离大约为y，毛细管另一端装有磁堵.当调节蓄水桶竖直，且蓄水桶中无气泡后，打开毛细管一端的磁堵，让蓄水桶的液面下降足够慢(准静态过程)，使毛细管中的流动保持层流状态，此时从毛细管一端射出的液体应呈抛物线状且平稳，通过测量液面在不同时刻的高度，即可实现流体黏度测量.

图1显示的实验装置的设计思路简洁，操作简单、测量误差较小，是很多高校基础物理实验的首选.依据流体力学理论，液体在圆管内处于层流状态，如果圆管两端的压强差为Δp，则在圆管内达到定常流动之后的流量Q是

(2)

其中，v是圆管内的速度分布函数，r是以圆管中心为起点的径向坐标.由式(2)可以看出，要想测量流体的黏度首先要知道圆管两端的压强差Δp.如图1所示，圆形毛细管与蓄水桶连接的一端的压强未知，可以用p表示；而另一端因与大气相连其压强应为大气压强p0，因此毛细管两端的压强差为Δp=p-p0.求解毛细管两端的压强差Δp(或p)可以从两种理论出发，即经典的牛顿力学理论和流体力学理论，得到的结果略有不同，下面就基于这两种理论，对毛细管两端的压强差Δp=p-p0进行分析.

3 基于牛顿力学理论分析毛细管两端压强差

对于连续的不可压缩、运动形式比较简单的流体，可近似看成质点组，如蓄水桶中的液体.当毛细管磁堵打开后，如果蓄水桶的内壁光滑且桶中的液面缓慢下降，对于低黏度液体的运动可以近似看成是落体运动(如图1所示)，蓄水桶液面以上是大气压强p0，假设液体中的压强是各向同性的，与毛细管位置等高的液面压强为p，则依据牛顿运动定律可以给出变质量问题的力学公式

(3)

dm1=-ρv1A1dt

亦即

因此式(3)变为

(4)

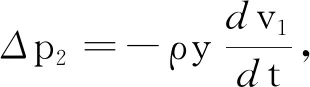
(5)

依据流量的定义，还可知道

Q=A1v1=A2v2

(6)

其中，A2(πa2)是毛细管截面积，v2是毛细管中流体的平均流速.

为了求解未知量y或v1，联合式(5)和式(6)，可以得到

(7)

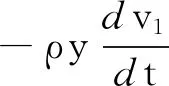
(8)

求解式(8)可以得到

(9)

其中，y0为初始时刻蓄水桶液面的净高度.测量一组不同时刻t对应的蓄水桶液面净高度y值，即可通过作图法拟合出待测流体的黏度η.

对毛细管两端压强差Δp做近似是毛细管法测量流体黏度常用的处理方式[1～6].为保证上述近似的可靠性，我们试比较式(4)中3种原因产生的压强大小.考虑到实验仪器设计的实用性，选取毛细管长L=150.0 mm，毛细管内径约a=0.5 mm，蓄水桶内径R=37.00 mm，内置液体为纯净水.如果初始时刻(t=0)蓄水桶液面的净高度y0=40.00 cm，可查在20 ℃时，水的密度

ρ=0.998 2×103kg·m-3

水的黏度

η=1.005×10-3Pa·s

选取北京地区的重力加速度g=9.802 m·s-2.我们计算了实验进行到不同的时刻，3种压强差的大小以及将被忽略的小量压强差占大量压强差的比重，计算结果如表1所示.

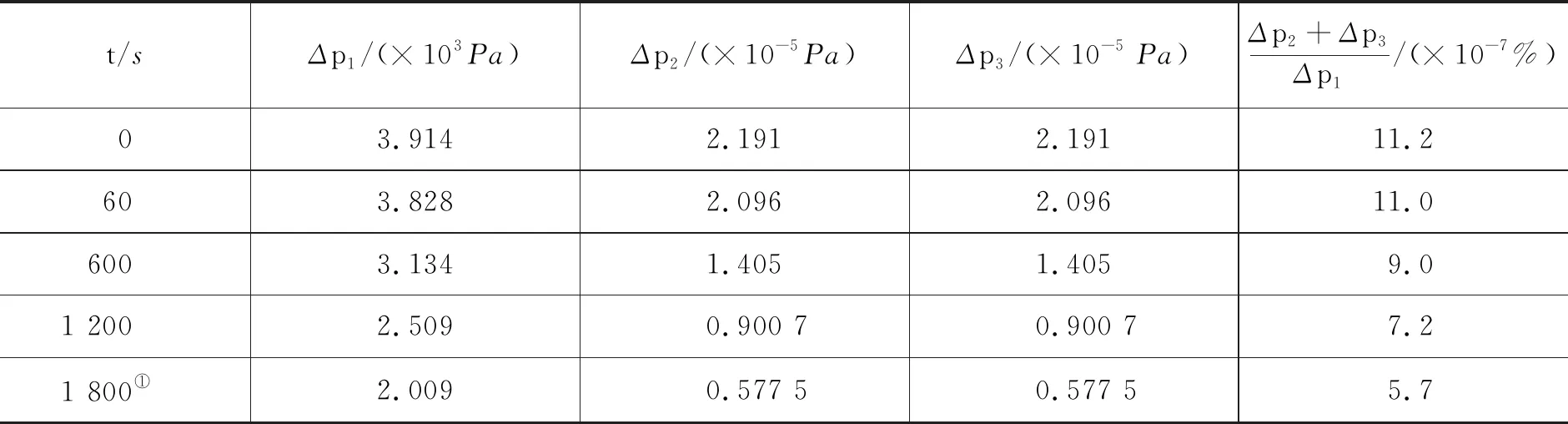
表1 式(4)中的3项压强差在不同实验时刻的大小及比例

①按照上述仪器设计参数，如果液面每下降约1.0 cm标记一次时间，测量约20组数据需要约1 741 s，为了计算简便取整为1 800 s.

随着实验时间的增加，这3种压强差都在减小，被忽略的小量占大量的比重越来越小.因此，在20 ℃时且在上述仪器设计参量情况下，忽略蓄水桶中液体的运动变化产生的压强差和蓄水桶中液体质量流失带来的压强差不会给实验带来太大误差，即使在其他温度下测量流体黏度也是如此.

4 基于流体力学理论分析毛细管两端压强差

简单的层流运动是流体力学描述的主要对象，基于流体力学同样可以推导毛细管两端的压强差.

蓄水桶和毛细管中的流体运动简化成层流状态，那就意味着也是无旋状态，则对于理想、正压、有势质量力、无旋且不可压缩重流体情形的流体运动，其运动方程适用于拉格朗日积分方程

(10)

其中，φ是速度势，f(t)是时间t的任意函数，由边界条件决定，对于某一固定时刻而言，f(t)在整个流场中取同一常数值.式(10)具有能量守恒的形式，是从能量的角度来描述流体的运动.

从蓄水桶的自由面A到毛细管入口B处，再到毛细管出口C，画出一条流线ABC，在流线AB段，因为蓄水桶截面相等，所以大部分v近似相同，则速度势

(11)

其中，x为从自由面A到流线上任一点的距离.因此，流线AB在两个标记点处有

(12)

其中，s是流线AB段的长度.AB段流线特定的长度很难计算，但可推知其取值范围在(y，y+2R).由式(12)可得

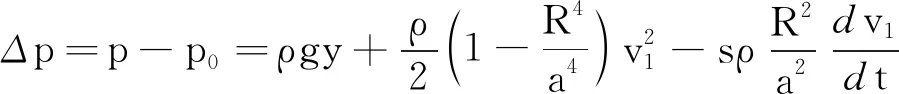
(13)

式(13)得到的静压强差Δp(等于上节用牛顿力学理论分析得到的压强差)也包含了3部分.第一部分是流线AB两端的净剩重力势能Δp′1=ρgy，该项是静压强差的主要贡献部分.第二部分是流线两端动能密度的变化量

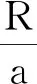
参照上一节实验仪器的设计参量及实验环境，我们比较一下流线AB两端动能密度的变化量、流线速度势的增量与流线AB两端的净剩重力势能之间的大小，计算得到的不同实验时刻的大小及比例如表2所示.

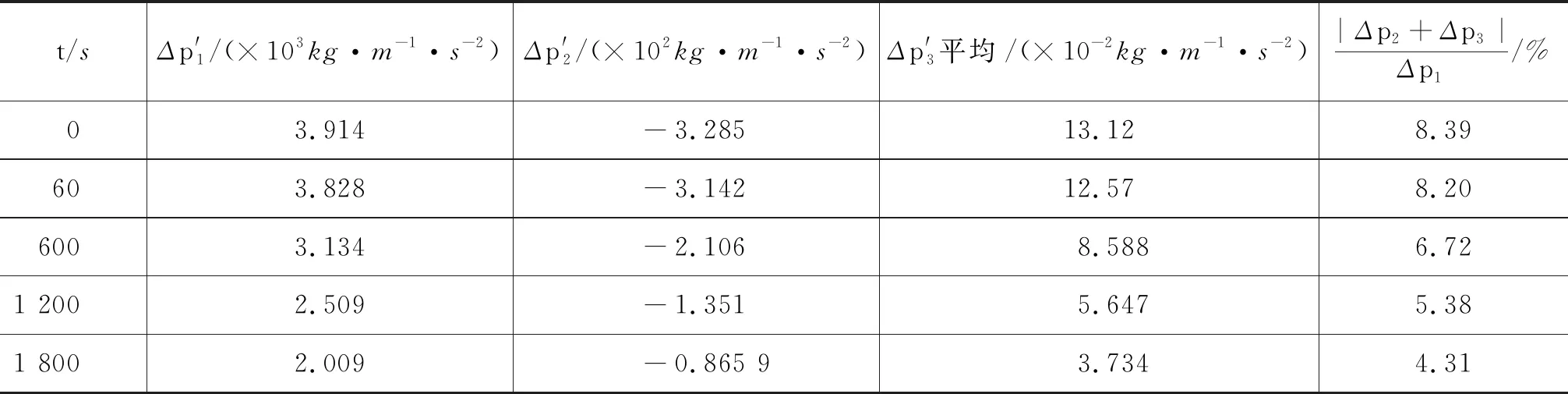
表2 式(13)中的3项在不同实验时刻的大小及比例

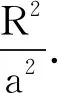
5 结束语

本文依据流体黏度的定义，对一种毛细管法测量流体黏度的简单装置，基于不同理论基础进行了理论误差分析.发现牛顿力学在分析低速且速度梯度比较小的流体运动时，引入的理论误差比流体力学理论小.无论从哪种理论出发，都可以得到相同的测量流体黏度的理论公式，并且都表明实验过程中不能以打开磁堵的时刻为实验开始的计时点，应该等待从毛细管一端射出的水流呈抛物线状且平稳之后再开始计时，以最大限度地减小误差.

简化后的理论公式容易理解，能够很容易地得出方程的解析解，实现了多领域知识融合和综合运用，本文的分析过程和结果为学生融合多领域知识，养成分析和解决问题的习惯提供了参照.