负二项回归模型的重对数律和强相合性

杨晓伟,张军舰

(1.广西师范大学 数学与统计学院，广西 桂林 541006；2.巢湖学院 数学与统计学院，安徽 合肥 238000)

负二项回归模型主要研究负二项型响应变量和一组解释变量之间的关系，广泛应用于计量经济学等领域中，例如分析面板负二项模型选择问题等。负二项回归除参数估计外，另一个重要功能是能够搜索最能解释或预测响应变量的子集，该过程相当于变量选择过程。在模型选择领域中最新文献有很多，它们以不同方式处理不同模型。查阅文献[1-3]并做详细调查，发现负二项回归模型选择方法很少被研究。负二项回归模型选择理论方法的缺失给实际应用带来诸多不便。为此，本文研究侧重于该类模型选择准则的渐近性质，包括AIC、BIC、MallowsCp和随机复杂度或负二项回归模型的最小描述长度。其渐近性研究的副产品是基于负二项回归模型构建了最大似然估计(MLE)的重对数律，即

其中d为某给定常数，‖·‖表示欧氏范数。由重对数律提供的MLE收敛速率在导出似然函数的精确近似时是非常有用的。

与本文相关的早期研究有Cameron和Trivedi[4]以及Qian和Field[5]，其重点仅限于Poisson模型和逻辑回归模型。本文考虑更一般的情况，即允许存在任何有意义联系函数的负二项回归模型。Qian和Field[5]提出的方法不能推出这种看似简单的理论表达，它需要一种实质性的证明技术。首先，这种泛化的对数似然函数失去了逻辑联系下拥有的简单性和一些好的性质，例如全局凸性，因此，要建立对数似然函数强的性质表示，使得各种可靠一致界限的给定变得更加困难。响应变量服从负二项分布，但并没有缓解这种困境。其次，联系函数具体表达的缺乏是另一个困难因素，因此，需要对一些条件进行限定，并适当地调整联系函数以获得所需的模型选择性能。

1 负二项回归模型选择

假设负二项回归设计数据服从两参数具有过离散性的负二项分布

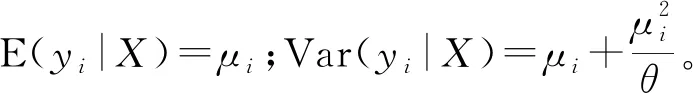
负二项回归的最大对数似然函数为

参数β的费希信息阵为

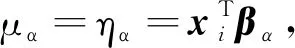
2 相关条件和主要结论

2.1 相关条件

为了证明主要结果，需要先给定以下假设条件：

(C1)存在正的常数b1、b2，满足b1n≤λ1{In(β0)}≤λp{In(β0)}≤b2n；

2.2 主要结论

定理1若条件(C1)～(C5)成立，则对任意正确模型α∈Ac，有

(1)

进一步，存在常数d>0，满足对任意α∈Ac，有

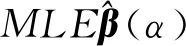
定理2在条件(C1)～(C5)下，对任意正确模型α∈Ac，有

(2)

定理3在条件(C1)～(C5)下，对任意错误模型α∈Aω，有

(3)

定理4若一个负二项回归模型满足条件(C1) ～ (C5)，则模型对于BIC和SCC准则都是强收敛的，而对于AIC准则是收敛的但不是强收敛。

3 主要结论的证明

证明的关键在于负最大对数似然函数的凸性、二次逼近、负二项标准分布的伽玛逼近以及独立随机变量的重对数律。凸性的应用是广泛的，另外渐近性理论的建立和线性模型M估计量的代表性文献有很多，具体可查文献[14-16]。

根据ξn定义和条件(C1)、(C2)，容易看出存在一个正的序列{τn}满足

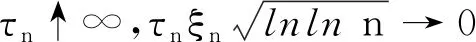
利用τn定义如下2个子集：

显然，B1⊃B2⊃B3⊃…⊃Bn，进一步定义：

令K(r,s)=f(r)-f(s)-f′(s)(r-s)，式中f(s)=θln(θ+es)，则

(4)

为方便证明，先给出几个引理。

引理1函数K(r,s)有以下几个性质：

①K(r,s)≥0对任意数值r和s都成立；

②K(r,s)是关于r的严格凸函数；

③ 存在常数c1，满足

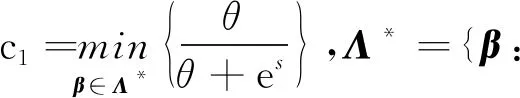
证明注意到K(r,s)=f(r)-f(s)-f′(s)(r-s)，f(s)=θln(θ+es)。由泰勒展开式，存在某数值v介于r与s之间，且

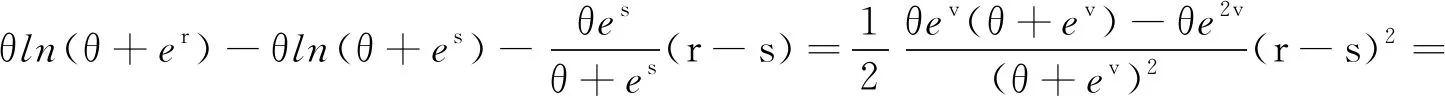
引理2设W服从负二项分布NB(μi,θ)，参数θ已知，对任意t>0，有

式中b为某一常数。

引理2由文献[17]中引理6.1修改而得，证明略。

引理4假设B是正定矩阵，对任意向量X≠0,V(X)=XTBX>0，则

式中λmin=min{|λ|：λ是矩阵B的特征值}，λmax=max{|λ|:λ是矩阵B的特征值}。

引理4由文献[15]中引理6修改而得，证明略。

引理5若条件(C1)～(C3)成立，则

(5)

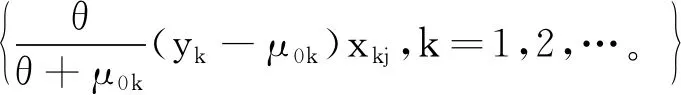
(6)

证明显然式(6)的结论来源于式(5)和条件(C1)，故仅需证明式(5)。不失一般性，假定xkj>0。利用条件信息yk～NB(μi,θ)，θ已知，由In(β0)的定义易证，对于j=1,…，p,

(7)

(8)

由条件(C1)，当n→∞时式(8)成立。

进一步，对于j=1,…，p,

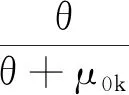
(9)

P{|(yn-μ0n)xnj|>εdnj}=P{|yn-μ0n|>εdnj|xnj|-1}。

(10)

由引理2，yn～NB(μ0n,θ)，θ已知。若令t=εdnj|xnj|-1，Eyn=μ0n，则

(11)

式中b为常数。注意到(C1)和不等式λ1{In(β0)}≤In(β0)(j,j)≤λp{In(β0)}，则

由上述不等式得，

由条件(C2)和ε的任意性，当n充分大时，有

(12)

根据式(10)～(12)，有

(13)

当n充分大时，由式(13)和条件(C1)，得

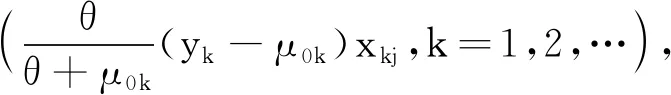
下面证明定理1。

定理1的证明对真实模型，要证明式(1)，证明

(14)

显然是充分的。应用引理1结论③，有

上述不等式的成立应用了引理4的结论。由条件(C1)，

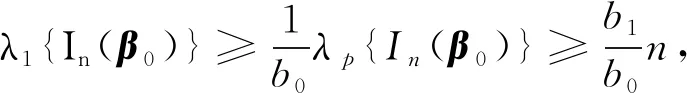
(15)

另一方面，利用式(4)、(6)，

(16)

(17)

由式(15)～(17)，存在b6>0，使得

(18)

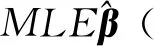
(19)

因为序列{τn}是尽可能慢的趋于无穷，则由式(19)可得式(14)。

(20)

从而推出式(19)是正确的。根据引理1③的结论，对于式(4)，有

(21)

(22)

另一方面，根据引理5，存在一个正整数序列{ni↑∞}满足

故当ni充分大时，有

(23)

由式(23)，当ni充分大时，有

(24)

由条件(C1)，

(25)

同时，当n充分大时，有

(26)

由式(25)、(26)，当ni充分大时，

由式(21)、(25)，当ni充分大时，

(27)

类似地，

(28)

结合式(24)、(27)、(28)，当ni充分大时，

由式(26)，

(29)

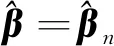
(30)

显然，式(30)与式(22)是矛盾的，即式(20)的假定是错误的。因此，对正确模型，

是成立的。定理1证毕。

下面证明定理2。

定理2的证明根据定理1的证明，若要证明式(2)，即证式(31)。由H(β,n)的定义可知

(31)

(32)

结合引理5的式(6)和定理1，得

(33)

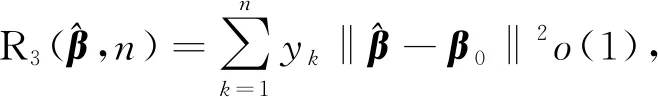
(34)

下面证明定理3。

(35)

定义

(36)

利用引理1结论③、式(4)、条件(C4)，可得，

(37)

类似地，由式(16)可证明

(38)

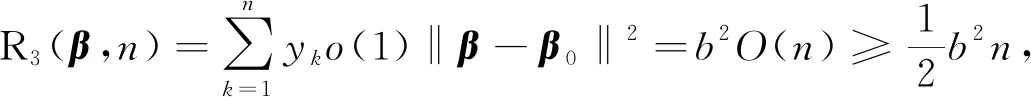
(39)

根据式(4)，有

(40)

联立式(37)～(39)，则式(40)、(36)成立，随之式(35)成立。定理3证毕。

本章最后证明定理4。

定理4的证明由于Fisher信息阵的行列式|I(β(α))|通常是O(npα)阶的，SCC和BIC惩罚项都是关于模型维数pα的递增函数且是O(lnn)阶的，从定理2和定理3的结论可推出SCC和BIC都是强相合的。由于AIC惩罚项为O(1)阶，故不一定是强相合的。但AIC显然是相合的，因为当n充分大时，正确模型的标准误差几乎必然小于任何错误模型且大于τn。定理4证毕。

4 后续工作

本文基于响应变量服从负二项分布，且候选模型依据可用解释变量作为假设前提获得渐近结果。由于实际应用中可能存在一些潜在变量，这些变量也会影响响应变量，在这种情况下，对响应变量可引入混合负二项分布来建模，利用过度离散参数来解释潜在变量的影响。查阅文献[8]第6章过度离散对数线性模型的详细内容可发现，将本文的渐近结果扩展到上述情况是非常困难的，但对于模型选择仍应关注那些可用解释变量。当然对于混合负二项分布(可模仿文献[21]中的证明来表示)能够获得类似引理2的结果，同时也可得到与定理1至4相同的结论。将渐近结果推广到除具有对数关联之外联系函数的负二项回归模型仍在研究之中，这些研究不仅涉及模型选择标准，还有许多其他模型选择方法，例如分层贝叶斯法[22]和Lasso[23]等，本文的结果可能不适用。另外，除确定模型选择标准并评估其渐近性质之外，还存在针对大量候选模型如何执行模型选择的计算问题，特别当候选模型数量(通常为2p)很大时，这将变得尤为重要，后续的工作也会对此问题进行更深入地研究。