非齐次GM(1,1)幂模型及其应用

马光红， 魏 勇

(西华师范大学数学与信息学院， 四川南充 637002)

0 引言

自邓聚龙教授提出灰色系统理论以来， 灰色模型被广泛应用于军事、 医学等领域， 为人们解决了许多实际问题[1]. 在研究灰色模型的过程中， GM(1,1)幂模型是GM(1,1)模型、 Verhulst模型的扩展. 对于GM(1,1)幂模型而言， 模型中幂指数及响应中参数的求解较为复杂， 研究相对较少. 王正新等[12]提出了GM(1,1)幂模型的幂指数的求解方法并讨论了幂模型的一些相关性质； 李军亮等[13]对幂模型进行扩展， 研究了非等间距的GM(1,1)幂模型； 文献[16]提出分数阶的GM(1,1)幂模型. 为提高模型的建模精度， 学者从幂指数、 背景值、 初始值、 灰导数等角度出发对模型进行改进. 文献[14]对GM(1,1)幂模型的灰导数进行优化. 文献[17]对模型的背景值进行优化， 文献[15]对初始条件进行优化. 在这些模型中， 大多都将原始数据当做齐次来处理， 实际上有部分数据并不都满足齐次这一特性， 于是采取此类方法建模并不太准确. 对此， 有学者研究非齐次模型， 并对非齐次模型进一步改进， 如： 改进灰导数、 改进初始值、 对模型直接建模等. 在文献[2]中提出了非齐次指数序列的GM(1,1)模型， 得到新的灰色微分方程及其白化微分方程； 文献[5]对GM(1,1)模型的灰色作用量进行优化， 用b1+b2k代替b， 即灰作用量随k的变化而变化； 文献[7],文献[11]提出Verhulst模型的直接建模法， 减少了数据还原， 但这些对非齐次模型的研究均在于GM(1,1)模型及Verhulst模型.

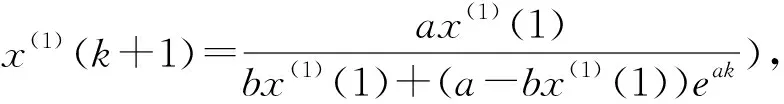
1 非齐次的GM(1,1)幂模型

设X(0)为非负原始序列且X(0)=(x(0)(1),

x(0)(2),...,x(0)(n))，X(1)为X(0)的1-AGO序列，X(1)=(x(1)(1),x(1)(2),...,x(1)(n))， 其中

x(1)(k-1))(k=2,3,...,n).

定义1称

x(0)(k)+az(1)(k)=

(b1+b2t)(z(1)(k))m(k=2,3,...,n)

(1)

为非齐次GM(1,1)幂模型的灰色方程.

定义2称

(2)

为非齐次GM(1,1)幂模型的白化微分方程.

由常微分知识对(2)式的白化微分方程求解得时间响应式

事实上， 将(2)式两边同除以[x(1)(t)]m得

(3)

令y(1)(t)=(x(1)(t))1-m, 则

(4)

(3)式变形为

(5)

不妨令

(6)

对(6)式求解得

y(1)(t)=c1e(m-1)at

(7)

将c1看做关于t的函数， 对(7)求导可得

(8)

将(7)、 (8)带入(5)化简有

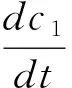
(9)

对(9)式积分

(10)

其中c为任意常数.

将(10)带入(7)式有

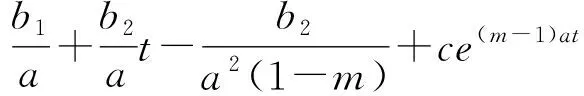
(11)

故

(12)

将(12)式在t=k+1离散化得到

累减还原x(0)(k+1)=x(1)(k+1)-x(1)(k)

(k=1,2,...n-1).

性质1当m=0,b1≠0,b2≠0时是文献[19]的表达式，即

(13)

为非齐次GM(1,1)模型；

性质2当m=2,b1≠0,b2≠0时, 即

(14)

为非齐次的Verhulst模型；

性质3当m=0,b2=0，b1≠0， 此模型退化为传统GM(1,1)模型；

性质4当m=2,b2=0，b1≠0， 此模型退化为传统Verhulst模型.

2 参数m;a,b1,b2,c的求解

对于GM(1,1)幂模型而言， 对参数的求解方法有多种， 文献[12]采取传统的方法求解参数， 即利用最小二乘法； 文献[20]通过最小二乘法求出参数表达式， 构造目标函数利用相关软件如Matlab进行求解； 对Verhulst模型， 大多文献采用最小二乘法求解参数； 文献[22]通过构造参数的表达式， 采取算术平均或者几何平均近似替代相应参数； 而GM(1,1)模型中参数的求解方法较多， 如最小二乘法， 最小一乘法、Lingo搜索等. 在利用最小二乘法或者最小一乘法求解参数时， 都避免不了模型中背景值z(1)(k)的应用， 由于背景值构造的差异， 难免会产生一定的误差. 本文利用文献[21]求解GM(1,1)模型中参数的方法(即利用多个值的算术平均近似替代最终参数的值)， 对非齐次GM(1,1)幂模型的参数进行求解， 减小由背景值造成的误差.

(I)按照文献[12]求解参数m， 即

(II)在时间响应式的基础上逐步求解a(k);

c(k);b2(k);b1(k).

首先对(11)式进行离散化得

当t=k+1时,

(15)

当t=k时；

(16)

当t=k-1时；

ce(m-1)(k-2)a

(17)

(15)-(16)得

y(1)(k+1)-y(1)(k)=

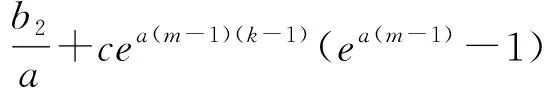
即

(18)

(16)-(17)得

cea(m-1)(k-2)(ea(m-1)-1)

即

(19)

(18)-(19)得

y(0)(k+1)-y(0)(k)=

cea(m-1)(k-1)(ea(m-1)-1)2

(20)

同理

y(0)(k)-y(0)(k-1)=

cea(m-1)(k-2)(ea(m-1)-1)2

(21)

用(21)除以(20)得

两边同时取对数得

(22)

将(22)带入(20)有

(23)

把(23)、 (22)带入(19)得

(24)

联立(15)、 (22)、 (23)、 (24)得

(25)

从上面的式子可以看出， 由于k值的不同， 参数a、b1、b2、c的取值也不同， 分别记为a(k);c(k);b2(k);b1(k)， 则

(26)

(27)

(28)

ce(m-1)ak)

(29)

值得注意的是， (15)、 (16)、 (17)中的a,b1,b2,c均会随着k的变化而变化的a′(k),c′(k),b2′(k),b1′(k)， 但由于相邻两项变化幅度不大， 在考虑(15)-(16)与(16-17)、 (18)-(19)、 (21)/(20)时， 将相邻两项中的a′(k),c′(k),b2′(k),b1′(k)视为同一推导的a(k),c(k),b2(k),b1(k)， 然而在变化的全过程中相距项数较多则是一个不可忽略的问题， 此时需要对a(k),c(k),b2(k),b1(k)综合考虑， 即下列步骤(III)是必须的.

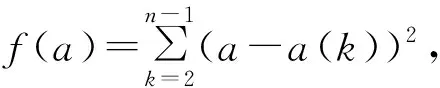
(30)

将(30)式计算出的a依次带入(28)及(29)式， 并利用与求解a相同的方法求解c;b2的估计值

(31)

(32)

同理将(30)、(31)、(32)带入(29)求解可得b1的估计值

(33)

3 实例分析

本文分别采用我国2002～2009年天然原油生产量的数据与南京市1997～2002年水泥运货量及我国历年人口数据作为实例进行模拟， 对比模拟精度.

例1本例以我国2002～2009年天然原油生产量的数据《中国统计数据应用系统》(见表1)为例， 数据来源于文献[7]， 对文献[7]中的数据分别建立传统的Verhulst模型(记为模型一)， 优化背景值后的Verhulst模型(记为模型二)， Verhulst直接建模模型(记为模型三)以及本文非齐次的GM(1,1)幂模型. 模拟结果及精度对比见表2.

表1 2002～2009年天然原油生产量

注： 表1的数据来源于文献[7]中的表3

本文模型(非齐次的GM(1,1)幂模型)的参数值：

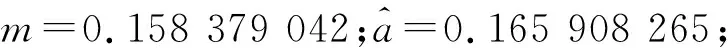
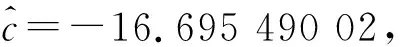
x(1)(k+1)=72.863 353 4+6.336 645 679k-45.381 083 46-16.695 490 02e-0.139 631 873k

累减还原x(0)(k+1)=x(1)(k+1)-x(1)(k).

模拟预测结果见表2.

表2 模拟结果与精度对比

注： 模型一、 模型二、 模型三的数据来源于文献[7]的表4.

结论： 对比表2的模拟结果， 模型二通过优化背景值后大幅度缩小了误差， 提高了精度； 另辟蹊径的模型三通过对数据直接建模， 虽未对模型的背景值进行优化但提高了建模精度， 且甚至比模型二优化背景值后的模型建模精度高； 而本文模型与前三个模型相比， 建模精度均优于前三个模型.

例2本例对我国历年人口数据建立传统的Verhulst模型、 优化背景值的Verhulst模型、 Verhulst模型的直接建模及本文非齐次的GM(1,1)幂模型， 非齐次的GM(1,1)幂模型直接建模用五种模型对人口进行模拟预测， 结果见表4.

利用2007～2011年数据建立模型(数据来源于文献[18])， 为方便将传统的Verhulst模型、 优化背景值的Verhulst模型及Verhulst模型的直接建模分别记为模型四、 模型五、 模型六.本文模型一和本文模型二的原始数据见表3.

通过计算模型六的表达式为

表3 我国历年人口

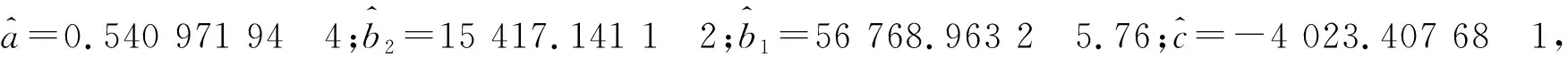
x(1)(k+1)=(104 938.830 8+28 498.96617k-58 958.755 89-4 023.407 681e-0.483 371 227k)1.119 2，累减还原

x(0)(k+1)=x(1)(k+1)-x(1)(k).

本文模型2的表达式如下：

x(0)(k+1)=(37 120.04613+183.535 9162k-735.392 653 1-29.050 575 07e0.249 575 401k)1.119 2

模拟值及精度对比结果见表4.

表4 模拟值及精度对比

文献中的模型四、 模型五并未对2012年的人口进行预测， 但本文利用模型六及本文模型1、 本文模型2对2012年的人口数据进行预测， 模型六、 本文模型1、 本文模型二的预测结果见表5， 2012年的原始数据为136 863.

表5 预测值及预测精度

注： 1)模型四与模型五的数据来源于文献[18],模型六通过文献[22]计算得到； 本文模型1为非齐次的GM(1,1)幂模型， 本文模型2为通过本文方法直接建模得到； 2)计算平均相对误差时先分别对五种模型的相对误差取绝对值， 再计算平均.

结论： 从模拟角度出发， 通过表4不难发现， 模型四的平均相对误差为4.92， 均大于其余模型的平均相对误差； 而模型五的平均相对误差为2.79， 小于模型四及本文模型1的平均相对误差； 模型六的平均相对误大于其余模型的误差而小于本文模型2的平均相对误差. 尽管本文模型1的平均相对误差大于模型六， 但是通过本文方法直接建模后的模型(即本文模型2)的误差明显比模型六小， 说明本文模型具有实用性. 从预测角度看， 模型六的预测精度明显低于本文模型， 并且对数据用本文模型直接建模后， 提高了预测精度， 说明非齐次的GM(1,1)幂模型具有较高的模拟精度， 且本文模型更实用， 并且原始数据是单调递增， 若对数据采取本文方法直接建模， 可以降低难度并提高建模精度. 对比表5与表4不难发现， 对数据进行直接建模， 不仅提高了建模精度， 而且大大降低了建模难度， 得到的模型不需要还原； 对于一系列单调递增的原始数据， 在建模过程中采取直接建模式是一种有效的方法.

4 结论

在研究GM(1,1)模型、 Verhulst模型及GM(1,1)幂模型的过程中， GM(1,1)模型及Verhulst模型均为GM(1,1)幂模型中幂指数分别为1与2的特殊情形， 由于原始数据不一定满足齐次指数形式， 因此有必要对不满足齐次指数形式的数据建立非齐次的GM(1,1)幂模型； 其次对不满足齐次指数的数据直接采取幂指数为1或者2建立GM(1,1)模型、 Verhulst模型并不准确， 因此本文通过建立非齐次的GM(1,1)幂模型， 利用微分方程及数据变换进行求解得到时间响应式， 对响应式离散化累减还原得到模拟值； 对于单调递增的原始数据， 可对原始数据直接建模， 如实例2， 直接建模后的模型不仅提高建模精度而且减少数据还原， 降低建模难度； 最后通过两个实例说明非齐次GM(1,1)幂模型可提高建模精度， 并且扩展了适用范围. 实际上， 利用本文模型能提高精度的原因在于本文的模型及求参数的方法. 首先GM(1,1)模型、 Verhulst模型中幂指数分别采取1与2， 但实际上并非数据都满足这一情形， 故如果采用幂模型建模可减小幂指数带来的误差， 其次在求解参数过程中背景值并未参与求解， 而是从时间响应式出发进行求解， 这减少背景值带来的误差； 说明此模型的可行性.