输入饱和的非线性系统多模型二阶段自适应控制器设计

吴 伟 ,王 昕 ,王振雷

(1.华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237;2.上海交通大学电子信息与电气工程学院电工电子实验教学中心,上海 200240)

1 引言

实际系统存在着非线性特性,其中输入饱和特性是常见的一类非线性特征.在航天器对接控制[1]、遥控系统[2–3]、导弹目标拦截系统[4]中都有所涉及.非对称饱和特性如果不加处理,则系统的暂态性能会很差,甚至导致系统的不稳定[5–6].例如,硬盘驱动的磁头移动太快会损坏硬盘,因而受到饱和特性的约束,Venkataramanan 提出离散复合反馈非线性控制(discrete-time composite nonlinear feedback control,DCNF),通过线性部分加快响应速度,非线性部分减小线性部分引起的超调完善了对硬盘读写的控制[7].J.M.G等人在幅值饱和的基础上增加了其一阶导数饱和特性[8].之后,多种针对线性系统的控制策略被提出,Tingshu等人通过计算系统吸引域的方法[9],广义扇区法与线性矩阵不等式技术[10]对系统进行了分析与设计.Castelan等人使用动态输出反馈补偿器对线性时变离散系统进行了控制分析[11].但在实际生产中,绝大多数系统本身带有复杂的非线性特征,随后,非线性系统带有输入饱和的情况也做了分析[12],证明了相关算法与系统的稳定性[13–16].纯反馈时滞系统[17]、未知控制方向的系统[18]、分数阶系统[19]、抗干扰复合系统[20]以及不确定系统[21]都讨论了各自存在输入饱和情况下的控制器设计,诸如backstepping控制[22–23]、神经网络控制[24–26]、滑模控制[27–28]、自适应控制[29]、动态面控制[30]等在处理输入饱和特性上有着很好的效果.为了改善输入饱和特性系统的暂态性能,Y.He等人设计了复合非线性反馈控制[31].施加的控制信号都是基于系统模型所给出的,模型的精确性直接关系到施加的控制信号是否合适.在初期,神经网络与模糊系统对系统的辨识效果较差,暂态性能难以达到要求,甚至可能带来系统的不稳定.相比于传统自适应控制,多模型二阶段自适应能够更快地逼近系统的真实参数[32–33],能够有效地改善系统的暂态性能.

基于改善暂态性能的目的,本文在传统自适应控制器上引入了多模型二阶段自适应机制,根据先验知识确定参数空间的范围,在边界处建立若干个模型,通过backstepping,逐步稳定系统并设计控制器,并给出了稳定性证明.相比于传统自适应控制器,通过增加鲁棒项,能够减小所需控制信号的幅值、超调与振荡.所设计的控制器能够保证系统中的信号半全局最终一致有界,跟踪误差收敛于一个较小的紧集内,最后进行数值仿真与应用研究,验证了本文所提出的控制器的有效性、优越性与实用性.

2 系统描述

考虑如下单输入单输出的执行器非对称饱和的非线性离散时间系统:

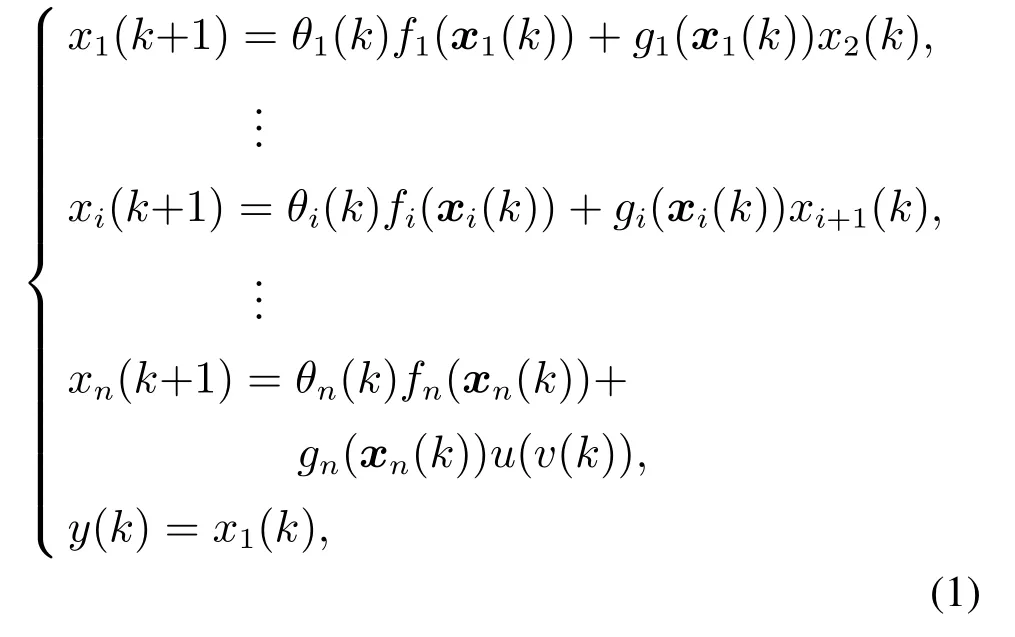
式中:xi(k)=[x1(k)x2(k)… xi(k)]T表示系统的状态;v(k),y(k)分别是控制输入信号与输出信号;θifi,gi∈(i=1,2,…,n)是系统中的非线性部分,其中gi,fi为已知的非线性函数,θi为未知参数;u(v(k))为系统的输入量,具有非对称饱和特性.其主要非对称饱和特性

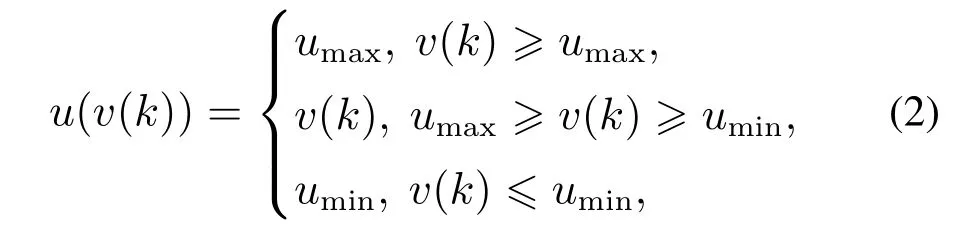
umax,umin为未知的饱和执行器的上下界.为简化证明计算,根据文献[36],该非对称饱和特性可由以下光滑的函数来代替(如图1所示):

图1 饱和特性函数Fig.1 Saturation function

定义函数

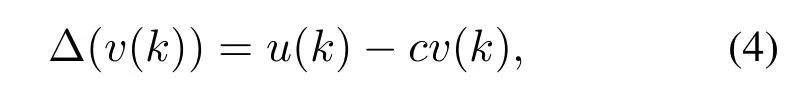
其中:c是一个正常数,u(k)和v(k)是时间k的函数.该函数仅用于稳定性证明,其中c在控制器的设计中并不需要知道其实际值.系统(1)可改写为增量形式:

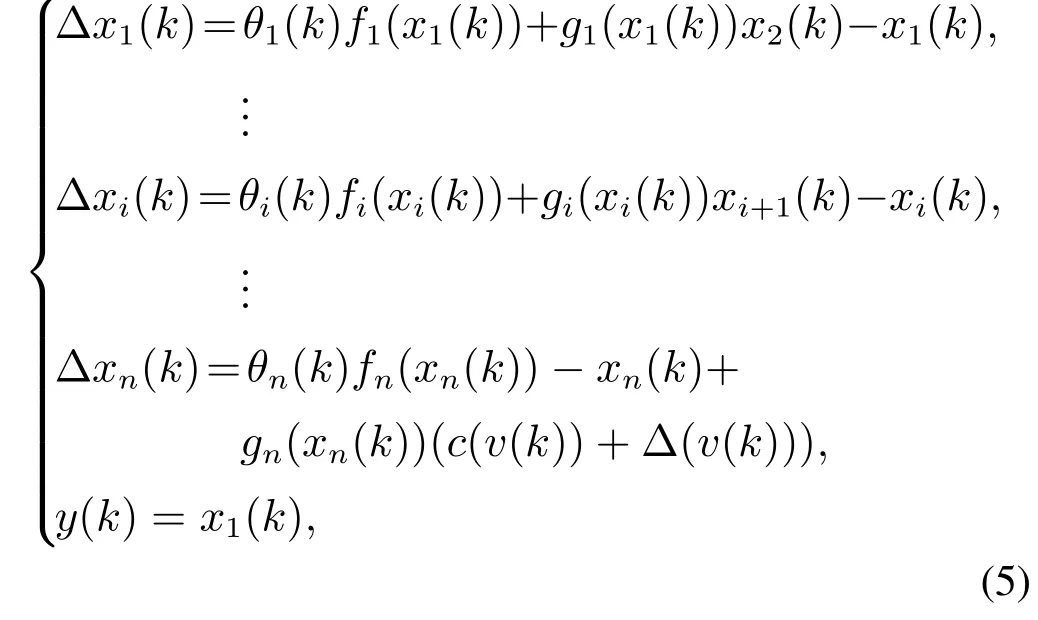
∆xi(k)含义为系统单位采样时间内各状态的变化量,i=1,…,n.

系统需满足以下几个假设:

假设1参考信号连续且有界;

假设2控制增益gi(·)是已知的,并且存在常数

假设3存在常数满足

假设4为已知的Lipschitz非线性函数;

假设5系统的未知参数向量θ位于凸集合内.

值得注意的是,假设2−3的上下界不要求已知,假设3为饱和函数一般性假设.关于假设4,Lipschitz非线性是非常常见的,具有相当大的实用性.假设5为二阶段自适应的一般性假设.

本文的目的是针对一类形如1的非线性系统,设计控制器,使其渐近跟踪已知的参考信号,误差最终收敛到0的小邻域内.

3 控制器设计

3.1 一阶段参数辨识

针对系统(5)设计如下的自适应模型集:

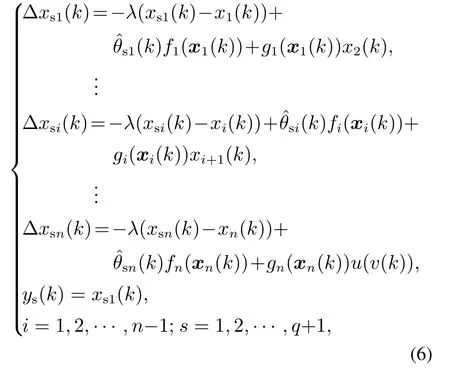
xsi为辨识模型的状态变量,为辨识模型的估计参数,定义参数辨识误差与状态辨识误差分别为esi=为待设计的常数,s=1,2,…,q+1为模型编号,q为未知参数个数,N=q+1个模型分布在由先验知识确定的参数空间的边界处.

选取如下的候选李雅普诺夫函数:

µ为自适应系数,一般取0.7左右.选取0<λ<1可以使式(8)小于0,辨识误差和参数估计误差趋于0,即

3.2 二阶段参数辨识

在一阶段参数辨识中,已对未知参数进行了初步的辨识,为进一步减少辨识误差,对上一节得到的N个模型进行凸组合.

引理1(凸包的性质)集合Ωm∈n,令covΩm为Ωm的凸包,则covΩm中所有的点均可以用Ωm中至多n+1个点的线性凸组合表示.

由引理1可知,如果系统未知参数θpi在k=0时刻位于covΩm(0)中,则存在一组系数αi满足

在k=k0时,θpi∈covΩm,即

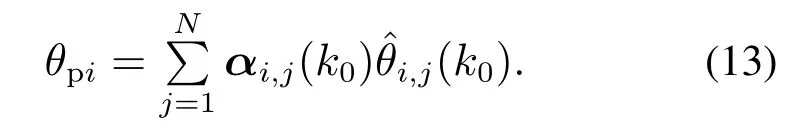
由一阶段自适应律(9)有

因此,在任意k >0 时刻,θpi都位于θi,j(k)的凸包covΩm(k)中,即一定有

式中:

建立系数模型

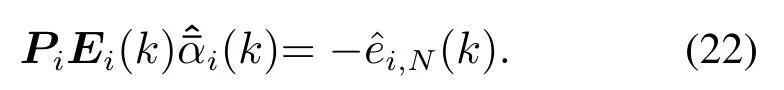
系数αi(k)由如下自适应律进行更新:

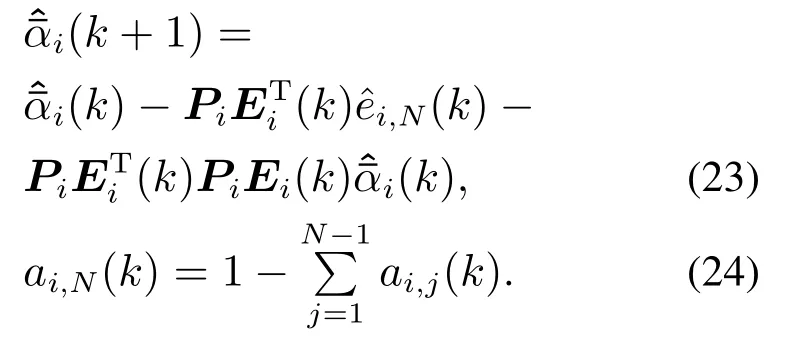
由上述算法,可以得到各个参数子集在k时刻的虚拟模型参数

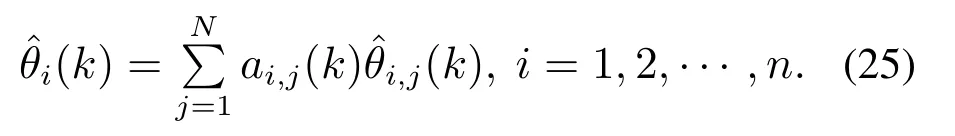
选取如下的候选李雅普诺夫函数:

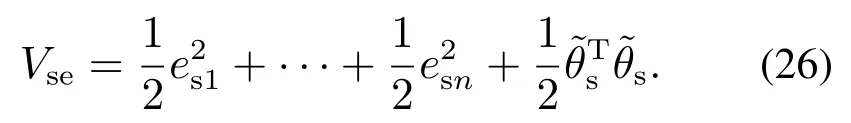
由式(8)(18)−(19)可得,凸组合后得到的李雅普诺夫函数在参数更新律(9)−(10)(23)(25)下,恒大于0,变化率小于0.

3.3 Backstepping控制

根据上一节的分析,辨识得到了未知参数θ的估计值ˆθ,根据该估计值,结合Lyapunov 定理与backstepping方法设计控制器.设计步骤如下:

选择候选李雅普诺夫函数为

考虑到tanh函数的特性

代入式(32),得到

选择以下候选李雅普诺夫函数:

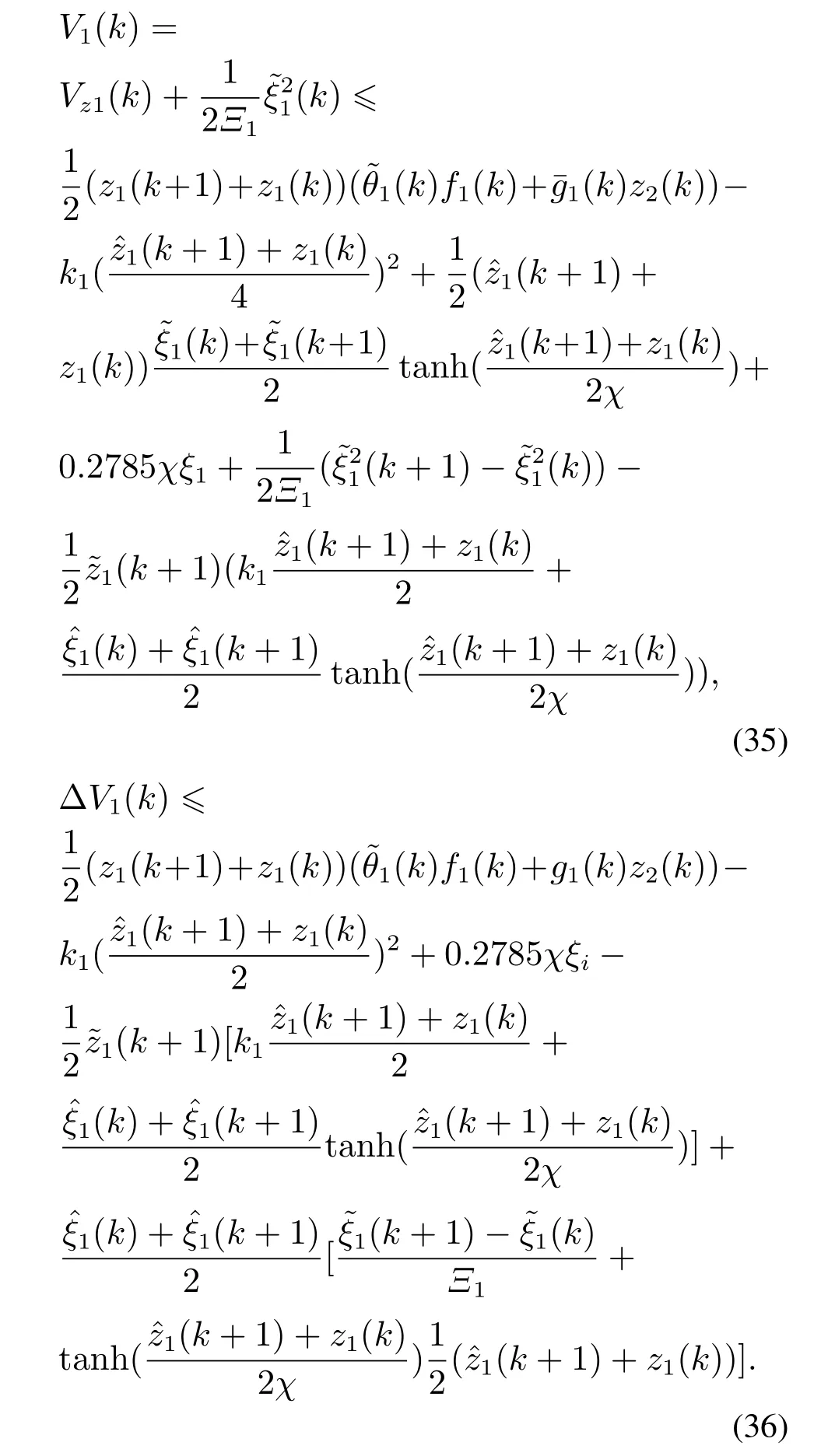
ˆξ1(k)的更新律如下:

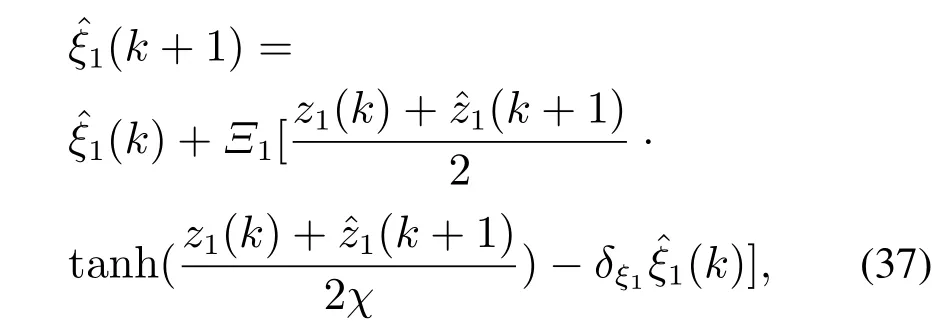
其中的δξ1是一个足够小的正常数,可取0.1∼0.5,目的是增强对状态、参数估计时的误差的鲁棒性.一步迭代后的虚拟控制律为

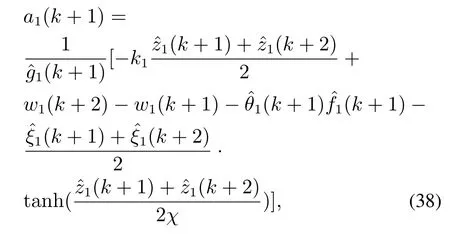
ki(i=1,…,n),k1为控制增益,可取5∼20.由Yang不等式有

τ是时间常数,与时间步长相关,一般取1.

选择候选李雅普诺夫函数:

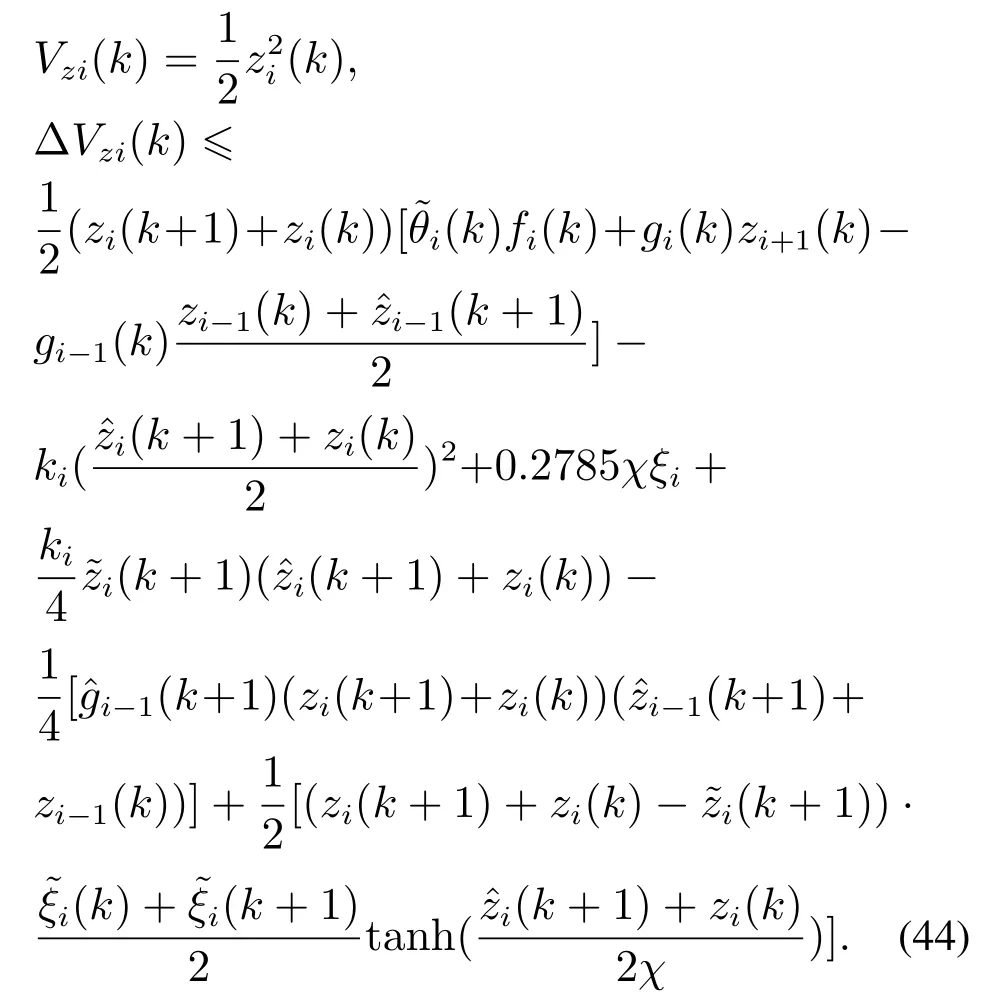
选取李雅普诺夫函数:

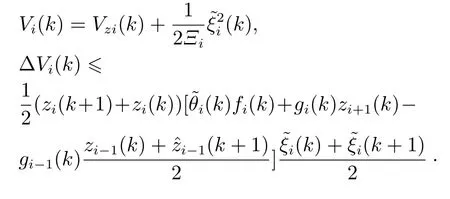
选取控制律为

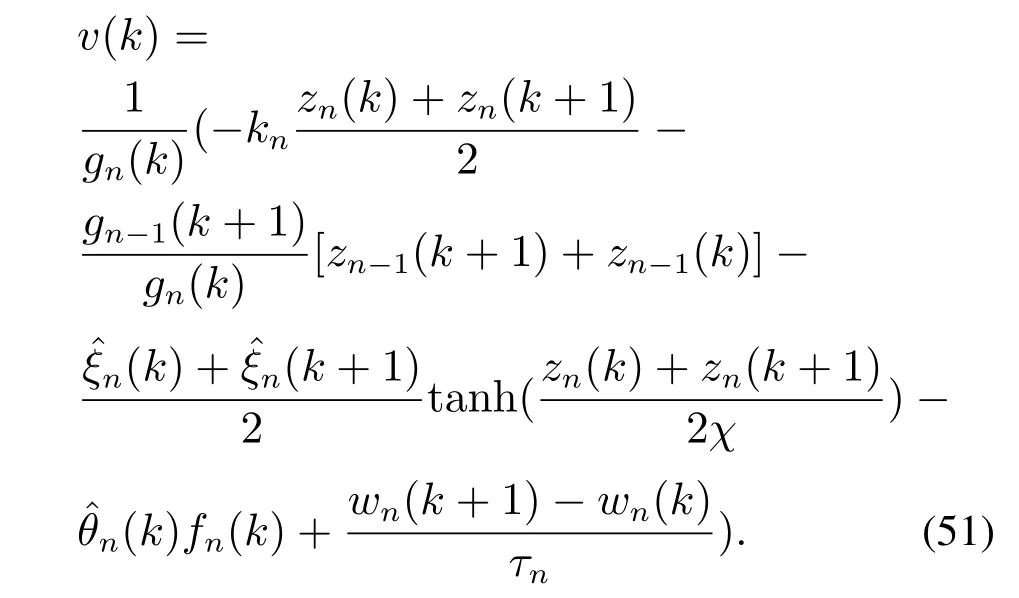
候选李雅普诺夫函数:

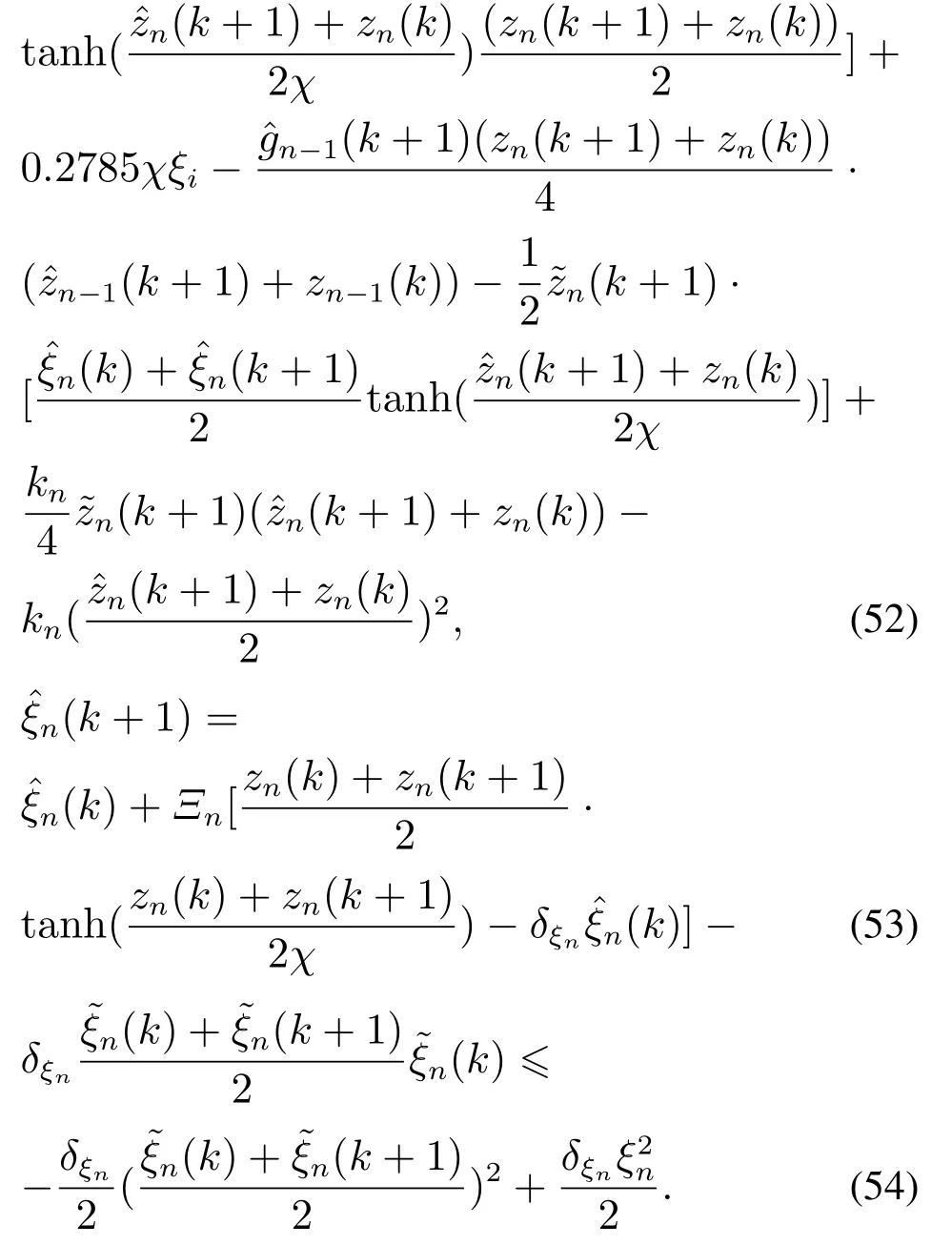
选取总体李雅普诺夫函数:

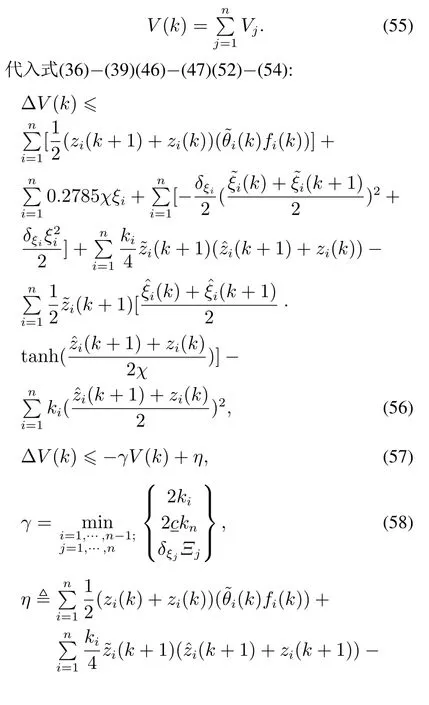
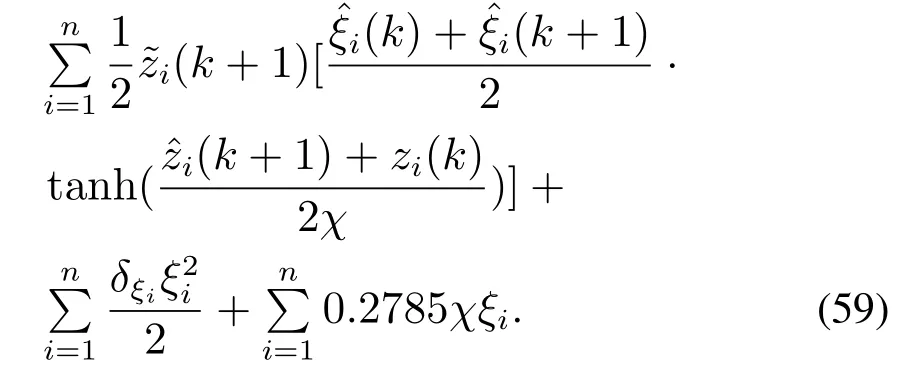
由式(11)可知,式(59)中的状态估计误差与参数辨识误差趋于0.式(59)可改写为

由Razumikhin引理和(57)−(58)(60)可知:该闭环系统中的信号均是半全局一致最终有界的.

4 仿真研究

4.1 数值仿真

考虑如下的输入具有非对称饱和特性的非线性连续时间系统[36]:

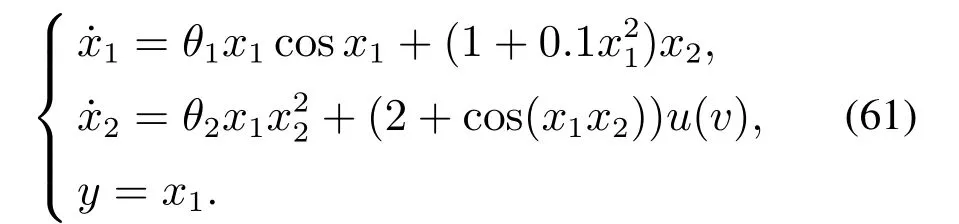
对其进行离散化采样,得到如下的输入具有非对称饱和特性的非线性离散时间系统:

其中:umax=40;umin=−45;Dt为系统采样时间;θ=[θ1,θ2]=[2,−1],θi∈[−3,3],i=1,2;单控制器模型初值选取为[3,−3];MMSLA共建立3个模型,初值分别为[3,3],[−3,2],[3,−3].不失公平性,组合系数初始值为[0.05,0.05,0.9],虚拟模型的初始值接近单控制器模型的初始值.

参考信号为

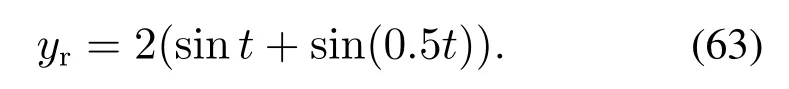
各控制器的设计参数选取如下:

针对未知参数p1,p2,模型的初值分别为[3,−3,3],[3,2,−3].实际对p1,p2的辨识模型数量分别为2,3个,如图2−3所示.

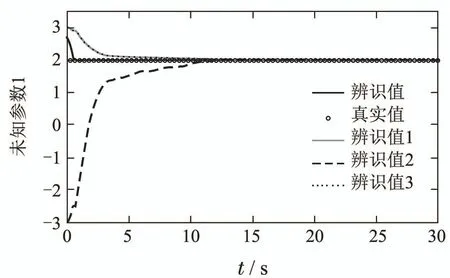
图2 MMSLA控制器未知参数1辨识Fig.2 Parameter 1 identification

图3 MMSLA控制器未知参数2辨识Fig.3 Parameter 2 identification

多模型与单个模型的差别仅在辨识上,多模型一阶段的参数辨识是各自独立的.由文献[34–35]有:单步计算量为4mn2+4m2n+2mn −m2+m+2.其中m,n为系统矩阵维度.凸组合系数计算的矩阵维度相比于系统矩阵要低一个维度,其计算复杂度为O(n2).多模型单步整体计算量为O(N ∗(4mn2+4m2n+2mn −m2+m+2)+con2),其中co是凸组合计算复杂度的常系数.理论上MMSLA 单步计算量小于单个模型的N+1倍.考虑到MMSLA能更快地收敛[32–33],参数收敛后若系统是时不变的,仅需要计算控制信号即可.针对系统(60),计算复杂度的比较见表1.

表1 计算复杂度比较Table 1 Computational complexity comparison

当m,n3 时,针对较大范围不确定参数,MMSLA计算效率优于单个模型.当系统更为复杂、未知参数范围越大时,多模型占用的计算资源会越多.但是单个模型的收敛时间T也会快速增长,同时,还需忍受长时间的较差的暂态响应以及控制信号不匹配下可能出现的不稳定情况.长远来看,多个模型是值得的.

从图4−5中,可以看出,MMSLA控制下的系统对于跟踪所给定的信号具有较小的误差,暂态性能也更好.控制信号的饱和特性如图6−7所示.图8显示,误差是有界的,并最终收敛到一个充分小的紧集.图2−3、图9−10显示了未知参数的辨识,因MMSLA对未知参数的辨识收敛更快.施加的控制信号更加合适,能够使得系统输出更快更好地跟踪参考信号.综上,本文提出的控制策略能够产生一个有界的控制信号,满足非对称饱和特性,跟踪所给定的参考信号并有着相比于传统控制器更为优良的性能.

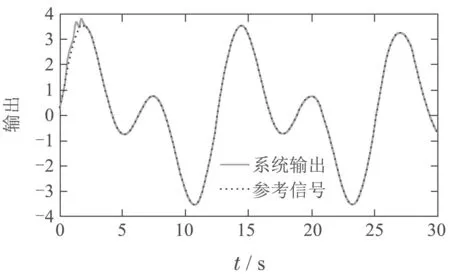
图4 单控制器系统输出Fig.4 Output of single controller

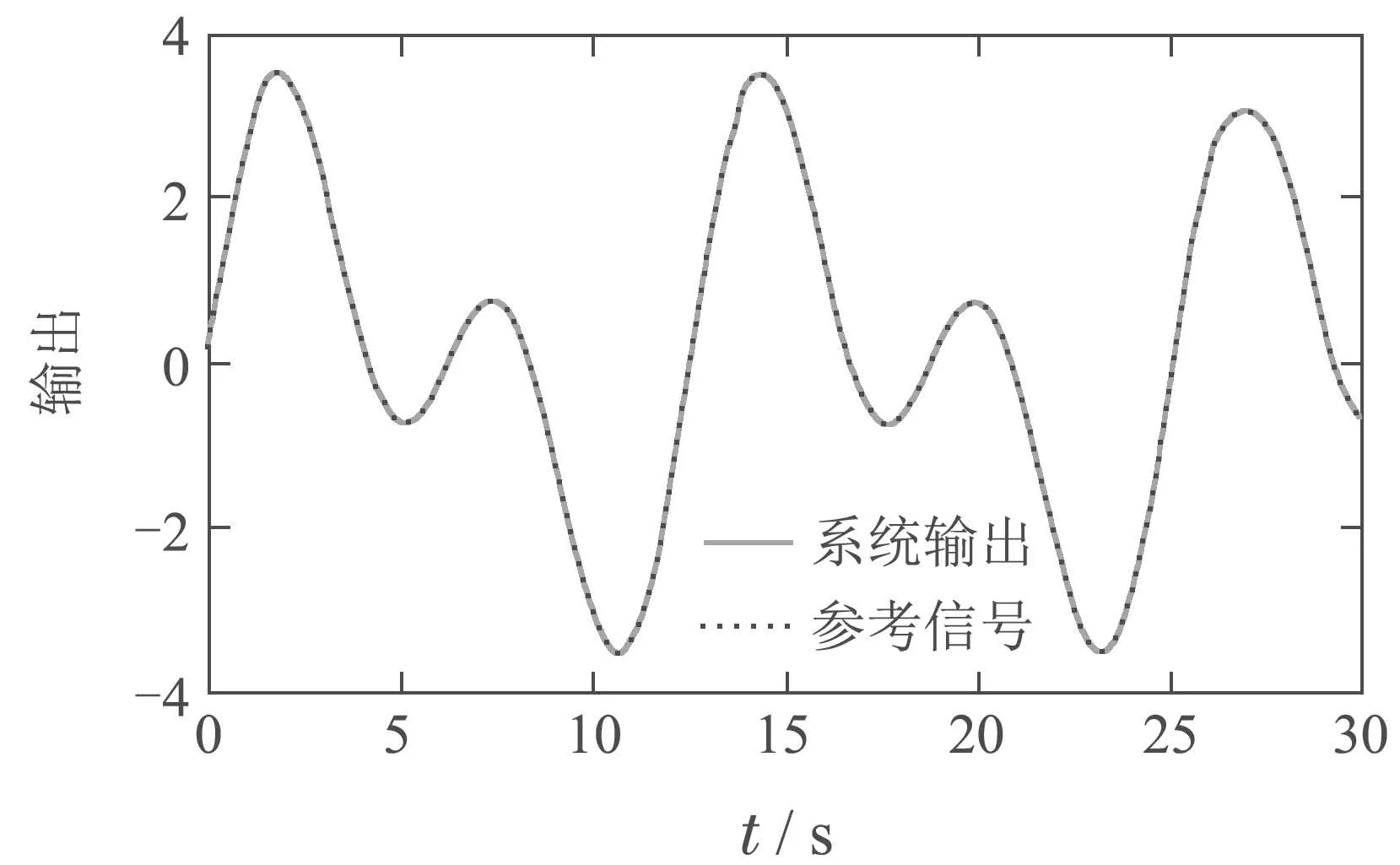
图5 MMSLA控制器系统输出Fig.5 Output of MMSLA controller

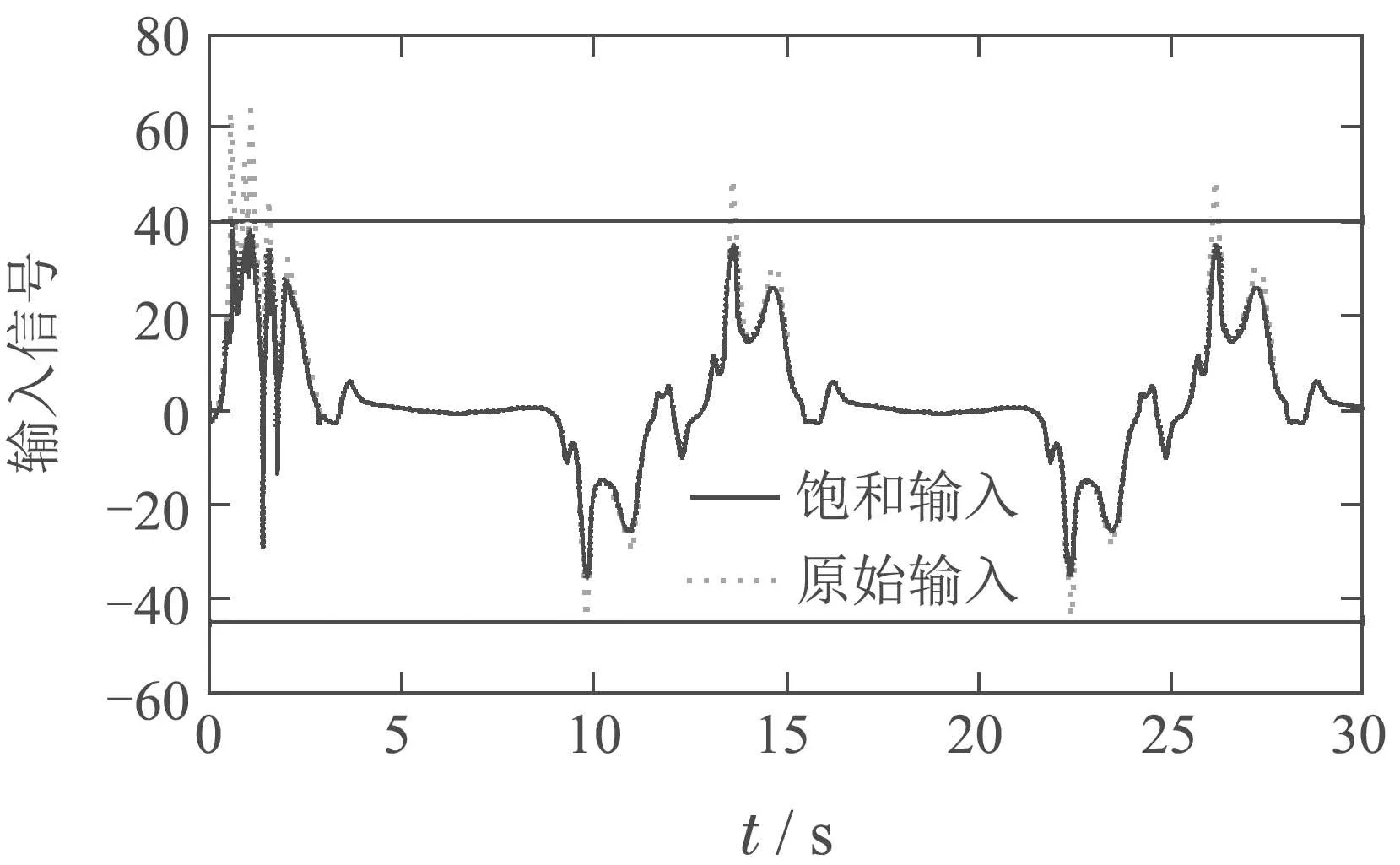
图6 单控制器系统输入Fig.6 Input of single controller

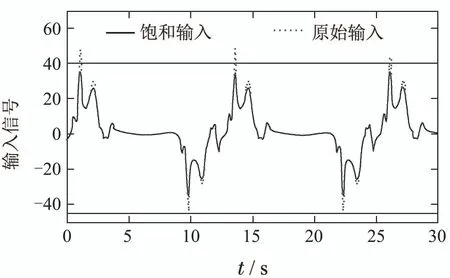
图7 MMSLA控制器系统输入Fig.7 Input of MMSLA controller

图8 系统误差对比Fig.8 Error in output comparison

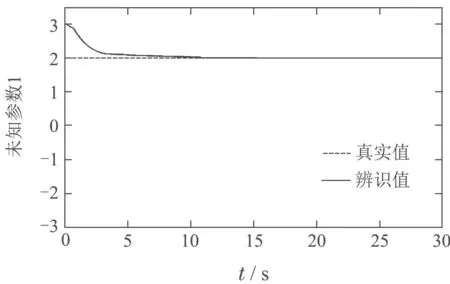
图9 单控制器未知参数1辨识Fig.9 Parameter 1 identification

图10 单控制器未知参数2辨识Fig.10 Parameter 2 identification

4.2 船舶仿真研究

为了验证本文所提自适应控制器的实用性,在船舶航向控制系统中进行仿真研究应用.船舶运动的几何学在坐标系(X0,Y0)中定义,而船舶本身的运动在与船舶固定的相对坐标系(x,y)中描述.船舶的运动如图11所示.

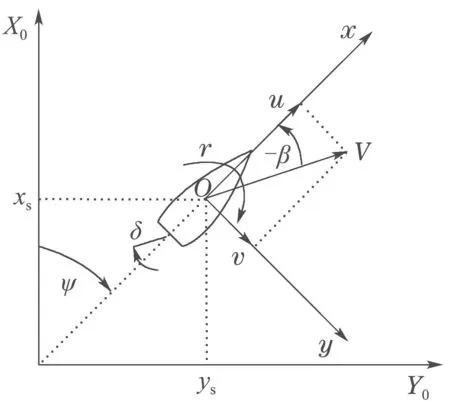
图11 船舶运动坐标系Fig.11 Ship motion coordinate system

系统中,被控参数为航向ψ(t),控制参数为舵角δ(t).从牛顿动力学定律出发,推导了描述船舶动力特性的方程.假设大型排水船(如油轮)的横向运动可以忽略.船舶的动力学特性的数学模型采用了Astrom与Wittenmark(1989)给出的游轮的模型,为非线性三阶微分方程[37].

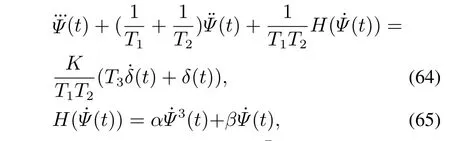
游轮空载时:

游轮满载时:

对于大多数船舶来说,航向角和其速度变化都需保持在一定范围内.对于这一假设,转向机的动态特性由式(68)给出:

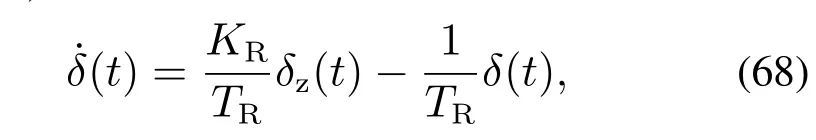
式中:TR=156 s,KR=96◦.

模型(64)可被改写为

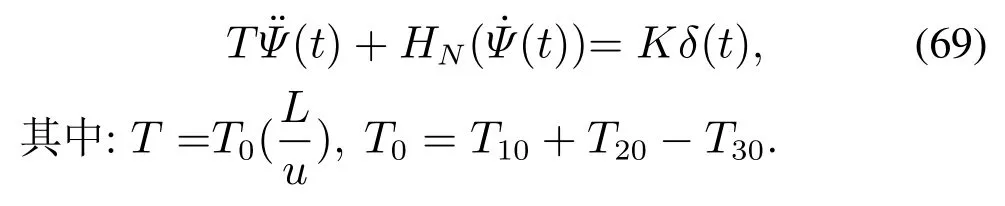
转化为状态方程:

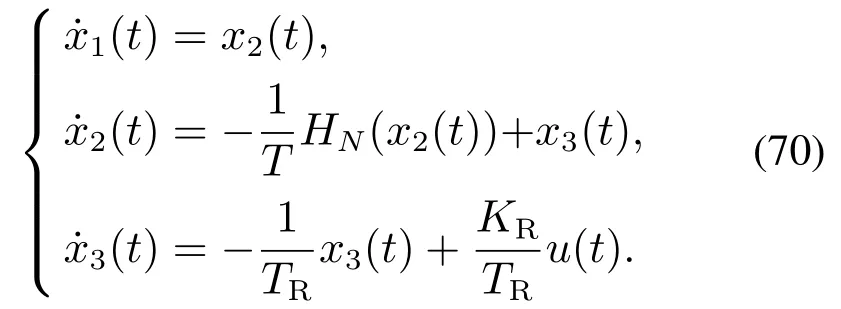
将其进行离散化,得到

∆T为采样时间,T,TR,KR为未知参数.

在船舶满载的情况下,得到的仿真结果如图12−19所示.由图13−15可知,MMSLA比单个自适应模型能更快地收敛.对比图12与图16,本文的控制方法所需的控制信号幅值相比于单个模型大大减小了,单模型控制器至少需要35◦,而MMSLA仅需要20◦.由图12,16,19可知,两种控制器在初期存在一定范围的振荡,但是MMSLA能更快的稳定下来,暂态误差更小.

图12 单模型控制器系统控制信号Fig.12 Input of single model controller

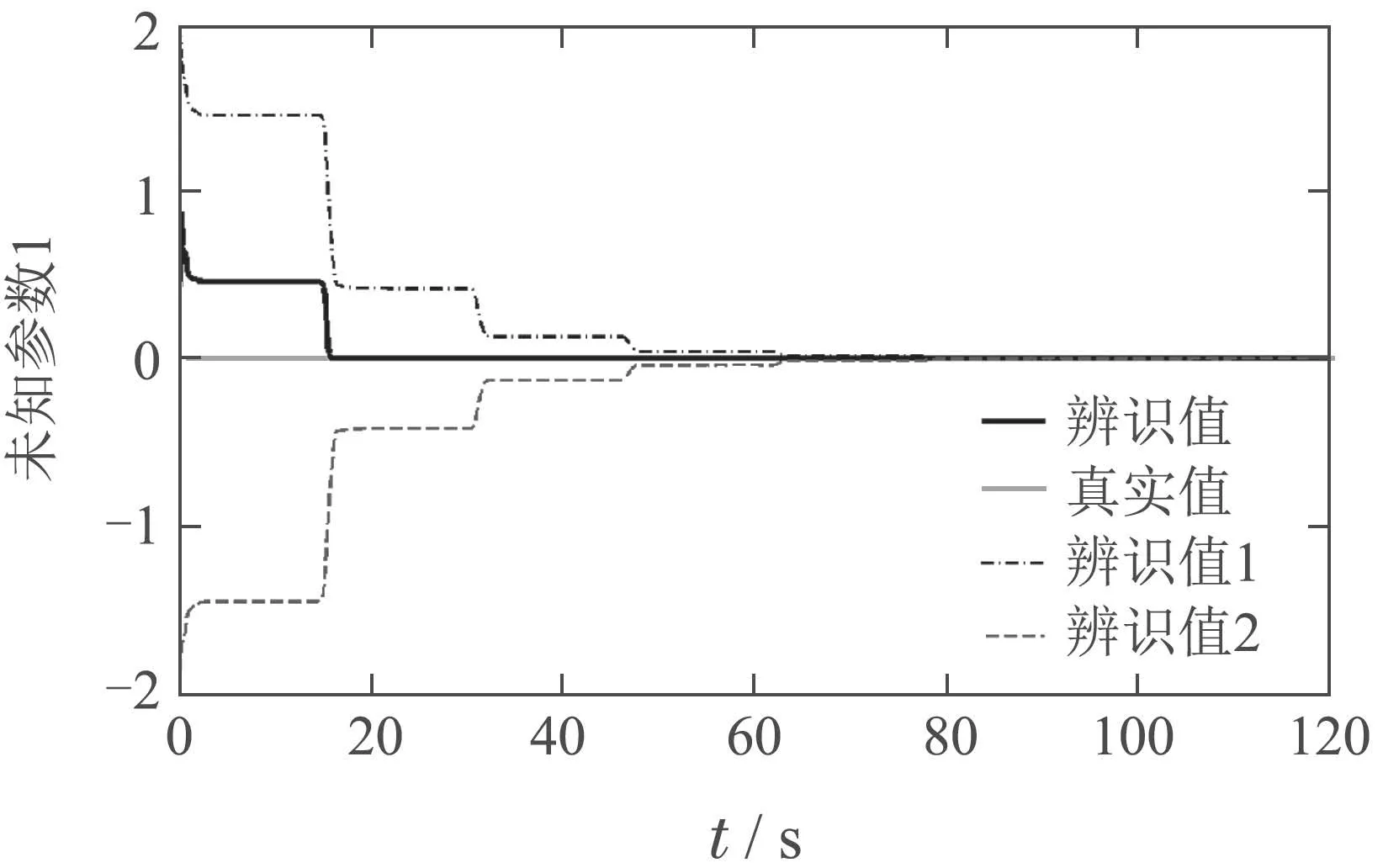
图13 MMSLA控制器未知参数1辨识Fig.13 Identification of unknown parameter 1

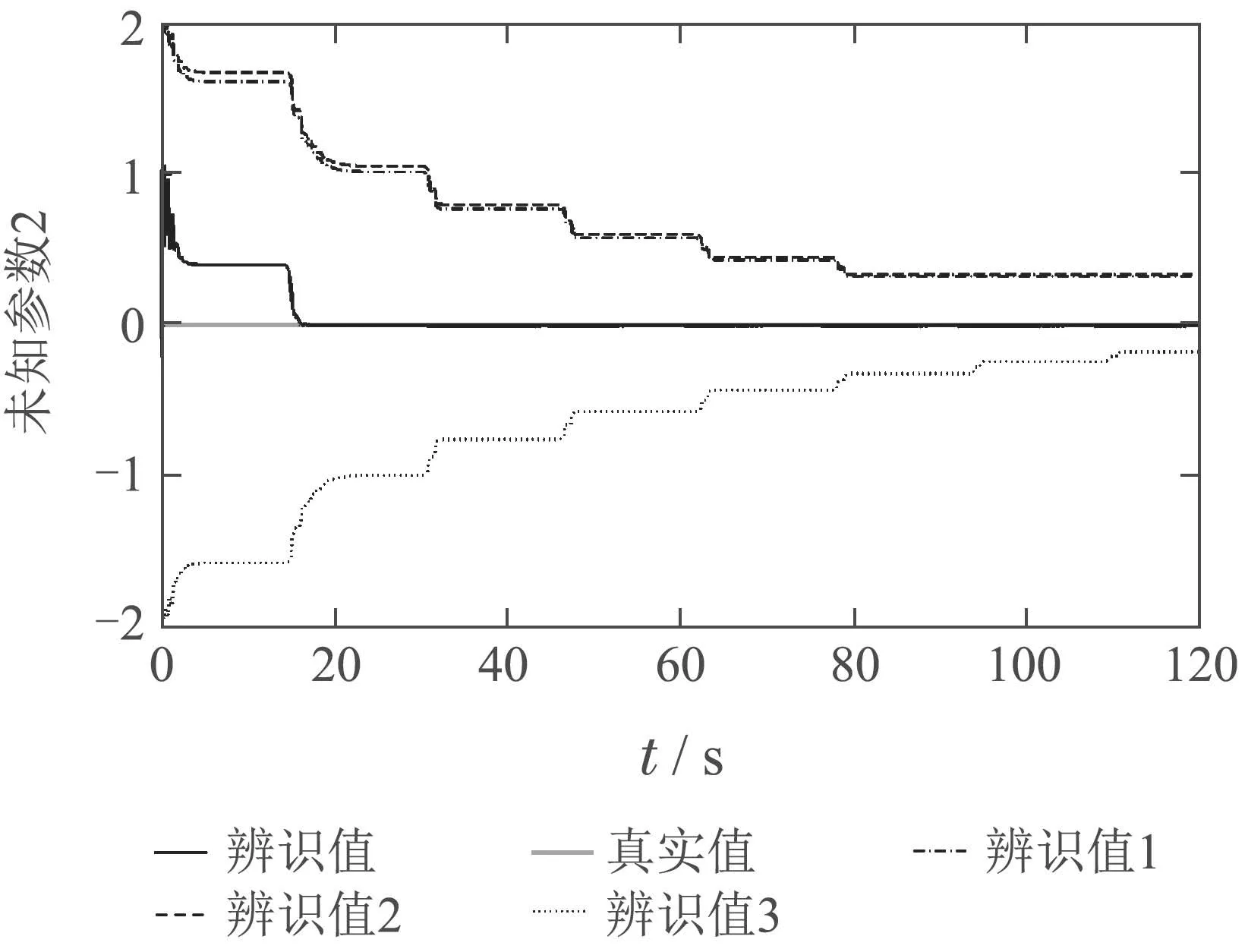
图14 MMSLA控制器未知参数2辨识Fig.14 Identification of unknown parameter 2

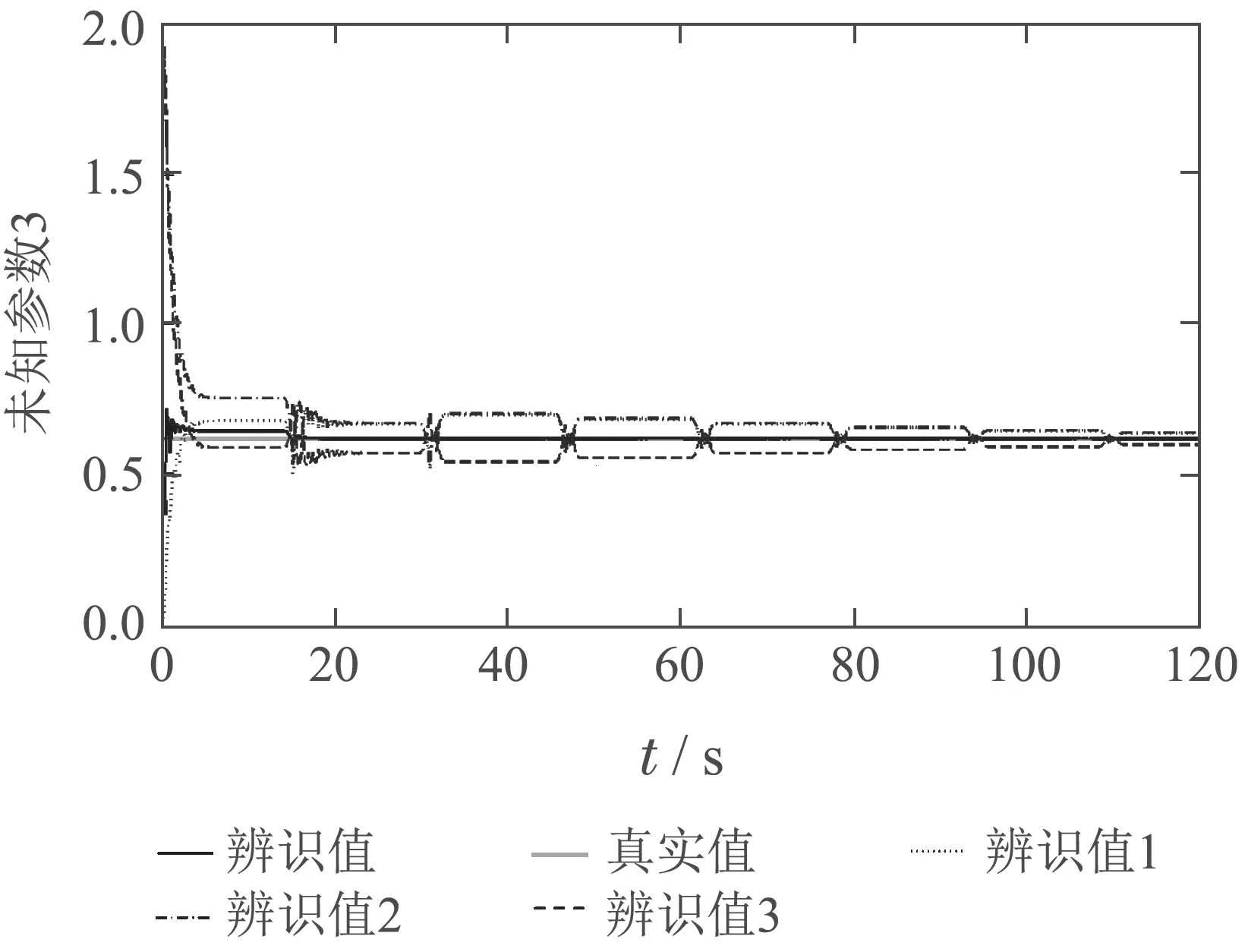
图15 MMSLA控制器未知参数3辨识Fig.15 Identification of unknown parameter 3

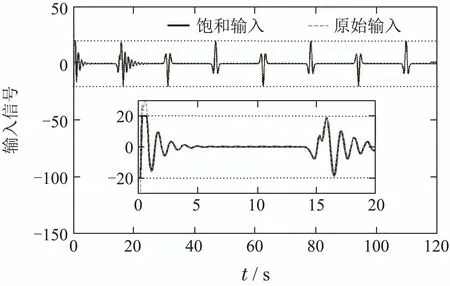
图16 MMSLA控制器系统控制信号Fig.16 Input signal of MMSLA controller

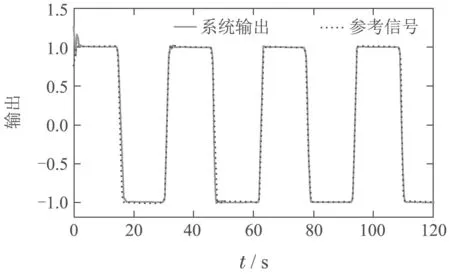
图17 单模型控制器系统输出Fig.17 Output of single model controller

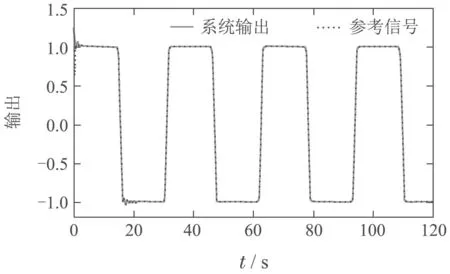
图18 MMSLA控制器系统输出Fig.18 Output of MMSLA controller

图19 跟踪误差对比Fig.19 Comparison of tracking error

5 结论

本文针对一类执行器非对称饱和的非线性离散时间系统设计了多模型二阶段控制器.首先根据状态误差对参数进行第1次辨识,在第2阶段,基于辨识误差依指数收敛的性质确定了凸组合系数,将多个模型组合为一个虚拟模型,在保证李雅普诺夫稳定的前提下,基于虚拟模型设计控制器,并证明系统的信号为半全局一致最终有界.最后,仿真研究表明,本文设计的控制器加快了参数的收敛,多个模型信息充分利用,改善了系统的暂态性能.