高炉铁水质量均方根误差概率加权集成学习建模
2020-06-11刘进进
刘进进,周 平,温 亮
(东北大学流程工业综合自动化国家重点实验室,辽宁沈阳 110819)
1 引言
钢铁是国民经济的重要支柱,高炉炼铁是钢铁生产的重要环节.典型的高炉炼铁系统如图1所示,可分为高炉本体、供料系统、煤粉喷吹系统、热风系统、出铁系统以及高炉煤气处理系统等子系统,其中高炉本体又由炉喉、炉身、炉腰、炉腹、炉缸等部分组成[1–3].在进行高炉炼铁时,由上料系统提供的焦炭、熔剂及铁矿石按照一定比例经传送皮带从高炉顶部装载到炉喉处,随后,形成混合后的焦炭层和铁矿石炉料层在炉身处交替填充进行布料操作;同时,在高炉的下部,热风系统和煤粉喷吹系统组合作业,将预热的空气、氧气、和煤粉沿炉周的风口鼓入炉腹中,使其在高温的作用下发生物理化学反应,生成大量的高温还原性气体;作为热量载体和还原剂的高炉煤气与不断下降的炉料经历复杂的物理化学反应,使得铁水从铁矿石中还原出来,不断向下滴落;上升的高炉煤气经过煤气处理系统得以回收利用,而最终生成的液体生铁和炉渣则从出铁口排出[4–6].
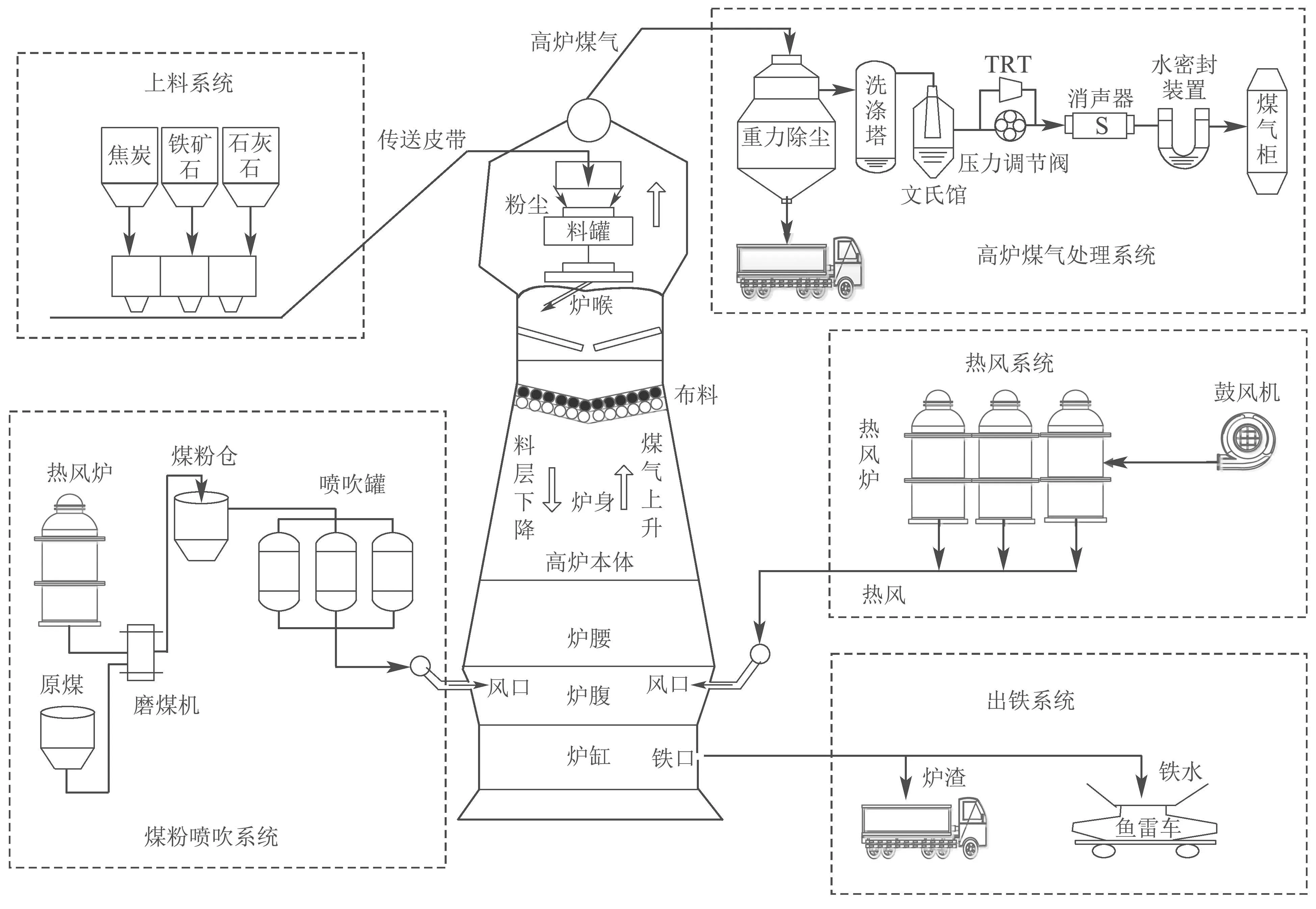
图1 高炉炼铁过程示意图Fig.1 Schematic diagram of blast furnace ironmaking process
为了实现高炉生产的优质、高产、低耗和长寿运行的目标,需要对高炉内部状态进行实时监测和有效控制.然而高炉炼铁过程是具有大时滞的非线性动态过程,炉内环境十分恶劣,反应核心区域温度高达两千多度,压强高达4倍的标准大气压,且存在固–液、固–固、气–液、气–固的转化以及固、液、气多态共存的状态,使得对高炉内部状态进行直接实时监测存在困难,进而影响高炉的优化控制[1–2].目前,铁水质量参数可以间接反应高炉内部状态,因此被广泛应用于高炉内部状态的监测和控制中,综合性的铁水质量指标通常采用铁水温度(molten iron temperature,MIT)、硅含量([Si])、磷含量([P])和硫含量([S])来衡量.
1)MIT是反应高炉炼铁过程能量消耗和炉内热状态的主要参数.若MIT过低,将导致高炉的顺行受到影响,进而影响后续的转炉炼钢的运行性能,致使综合冶炼成本上升.通常,高炉的出铁温度一般需要控制在1480◦C∼1530◦C.
2)铁水[Si]反映铁水的化学热,是铁水质量参数中最为重要的的指标.若[Si]过高,不仅会导致生铁的收缩率降低,引起铁水喷溅,而且还会影响石灰渣化的速度,延长吹炼时间.生产经验表明,低硅冶炼可以有效改善铁水质量,提高生产效率.
3)铁水[P]和铁水[S]是危害铁水质量的主要因素.[P]含量过高,会增加氧气和造渣材料的消耗,并且还会加重炉衬的蚀损;[S]含量过高,会增加生铁的脆硬性,降低铁水的流动性,从而影响铁水品质.
采用以上4铁水质量参数作为高炉运行状态的评价指标,可以比较全面的了解高炉内部的运行状态,为高炉生产日常操作和调节提供指导.但是,由于高炉内部环境恶劣、外部环境存在较大干扰,且受现有检测技术的限制,直接对高炉铁水质量进行准确的在线检测存在困难,且耗时耗力,通常的离线化验需要1∼2 h,存在较长的滞后.因此,建立准确可靠的铁水质量模型来反映当前及预测的内部温度和指标参数变化显得尤为重要.
目前常见的铁水质量模型有机理模型[5–6]、推理模型[7–8]以及数据驱动的智能模型[9–10].基于数据驱动的铁水质量建模方法是一种黑箱建模方法,并不需要深入了解高炉内部复杂的机理变化,仅仅通过数学工具和智能算法通过对过程数据进行处理,便可建立所需铁水质量模型,因而成为近年来高炉铁水质量建模研究的热点.现有数据驱动建模方法主要有多元统计分析方法[11–12]、神经网络(neural network,NN)建模方法[13–14]和支持向量回归(support vector regression,SVR)建模方法[15]等.但这些铁水质量预测模型大多只是对单一铁水质量参数硅含量或铁水温度的建模[16–17],并不能全面地反映高炉内部复杂的状态,且部分模型并未考虑高炉系统的非线性与动态特性.另外,铁水质量预测模型的建模速度和精度也是不容忽略的环节.为此,本文从实际高炉炼铁应用的角度出发,将致力于建立一种考虑非线性和动态特性,并且模型结构简单、速度较快、精度较高且易于工程实现的高炉炼铁过程多元铁水质量预测模型.从面向预测和软测量的建模角度来看[18],建立多元铁水质量指标预测模型需要解决如下几个方面的问题:1)问题1:如何更有效的提升高炉建模数据质量和从众多影响变量中选择最有效的建模输入变量;2)问题2:如何更好的拟合高炉炼铁过程非线性动态特性和提高数据建模的精度.
针对以上问题,本文从高炉炼铁实际应用的角度出发,提出图2所示的多元铁水质量非线性建模策略.针对问题1:首先,对高炉本体原始数据进行时间粒度的统一、正常数据的筛选和数据的归一化等数据预处理操作;其次,采用灰色关联分析法提取与铁水质量指标关联度最强的关键过程变量作为建模输入变量.针对问题2:首先,为了更好的反映高炉炼铁系统的非线性动态特性,引入非线性自回归模型(nonlinear autoregressive model,NARX);最重要的是为了提高数据建模的精度,提出一种基于Bagging 的均方根误差概率加权集成随机权神经网络(random vector functional-link networks,RVFLNs)算法,用于建立多元铁水质量指标模型.

图2 所提算法的建模策略图Fig.2 Modeling strategy diagram of the proposed algorithm
本文所提的均方根误差概率加权集成RVFLNs算法,其基本的思想是:1)为了提升集成学习的效率问题,采用具有快速建模速度的RVFLNs为子模型;2)为了解决传统基于Bagging的集成模型把所有好的和差的模型都分配相同比重的问题,本文所提算法提出一种均方根误差概率加权的思想进行子模型权重的分配.为此,本文使用核密度估计方法估计出子模型均方根误差集的概率密度函数(probability distribution function,PDF),进一步求出每个子模型均方根误差的概率分布情况,并把每个子模型的概率作为自身的权重,然后加权求和得到最终的均方根误差概率加权集成RVFLNs模型.随后,进行数值仿真验证和工业建模试验,并和其他几类铁水质量建模算法进行对比,结果表明,相对于对比算法,本文所提算法不仅具有很快的计算速度,而且具有更高的精度.
2 建模算法
2.1 数据的预处理及输入变量的选取
为了提高建模的数据质量,对高炉原始数据进行数据的预处理操作,具体过程如下:
步骤1时间粒度的统一.
由于各个过程变量是由不同采样频率的传感器测量而来,那么采集的数据的时间粒度是不一致的,必须将高炉铁水的出铁时间与本体参数的时间点进行对应.为此,依据数据时间标注及最近邻时间原则,进行人工匹配得到时间粒度一致的高炉炼铁过程的相关数据.
步骤2正常数据的筛选.
正常数据的筛选包括休风数据的剔除和采集异常值的剔除.由于每月需要对炼铁设备进行计划检修,属于可预见性的异常工况,检修时会进行休风操作,无出铁信息,无法作为建模数据,因此需要筛选出该部分数据将其删除.具体方式为:首先,依据交班记录确定高炉计划检修时间段;然后,剔除此时间段的高炉本体休风数据.
在高炉炼铁过程高温高压、多场多相耦合的恶劣的环境下,采集的数据存在异常值.使用异常的数据进行训练会增大模型的泛化误差,降低模型的精度.为了保证数据的合理性和有效性,必须对数据进行异常值的处理.本文选用具有简单的计算公式和可靠性能的3σ准则(拉依达准则)方法进行异常值的剔除,即数据偏差大于3σ的数据应该剔除.σ为上述筛选出的高炉本体数据的标准差,如式(1)所示:
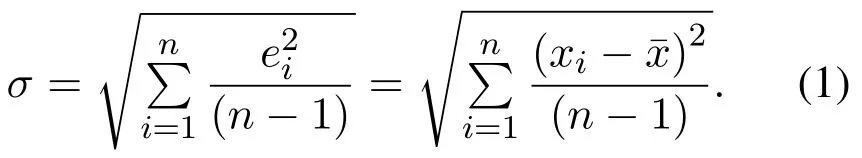
步骤3数据归一化.
为了有效的消除特征间的量纲不一致问题以及加速算法的收敛性能和一定程度上减小模型误差,本文选用最小、最大归一化,对高炉数据进行数据归一化处理[3].转化函数如下:
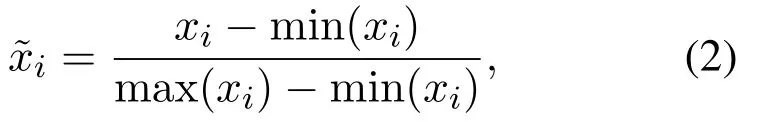
其中:xi,分别为第i个变量归一化前、后的取值,max(xi),min(xi)分别为第i个变量的最大值、最小值.归一化处理的到的数据xi∈(0,1).
为了从高炉众多过程变量中选择最有效的建模输入变量,从而提高建模的效率,本文引入灰色关联分析法.该方法通过对动态过程发展趋势的量化分析,求出参考数列和比较数列之间的灰色关联度,然后完成对系统内时间序列有关统计数据的几何关系的比较[19].与参考数列关联度越大的比较数列,则与参考数列同步变化的程度就越高,反之,则越低.具体实现过程如下:
步骤1确定分析数列.
反映系统行为特征的数据序列称为参考数列,影响系统行为的因素组成的数据序列称比较数列.设参考数列为式(3)中Z,比较数列为式(4)中Xi.对于高炉炼铁多元铁水质量建模系统,[Si]含量、[P]含量、[S]含量、铁水温度分别作为系统的参考数列,比较数列为m个影响多元铁水质量指标的关键过程变量.

步骤2变量的无量纲化.
为了消除高炉数据之间的量纲差异对灰色关联度分析结果的影响,本文选用归一化处理进行数据的无量纲化操作.
步骤3计算关联系数.
关联系数是比较数列和参考数列在各个时刻的关联程度,即高炉多元铁水质量与m个过程变量的各个对应点的关联程度.其数学表达式如式(5)所示:

在表达式(5)之中:|z(k)−xi(k)|被称为绝对值之差,被称为两级最小绝对值之差,被称为两级最大绝对值之差,ρ∈(0,∞),称为分辨系数.当ρ0.5463时,分辨力最好,本文取ρ=0.5.
步骤4计算关联度.
由于比较数列和参考数列曲线相应的点众多,使得信息过于分散不便进行整体比较.为此,把各个时刻的关联系数求平均,用于衡量比较数列和参考数列的相似程度,即关联度.关联度ri公式如下:

步骤5关联度排序.
关联度按大小排序,若r1>r2,则参考数列Z与比较数列X1几何关系更相似.
2.2 均方根误差概率加权集成RVFLNs建模算法
1)集成策略子模型的选择.众所周知,基于Bagging思想的集成模型相比单个模型建模会有更好的稳定性和更小的方差等优越性能.但是由于它是多个子模型进行建模,必然会牺牲一定的建模时间.如何提高集成模型的效率,是不容忽视的问题.解决此类问题,可以从两方面入手:第一,精简子模型的个数,即使用相对较少的子模型便可以达到集成模型该有的优越性能;第二,选择具有快速建模速度的子模型,从而挺高集成模型的效率.对于第1点,本文通过实验确定了满足精度要求的最小子模型个数.对于第2点,本文采用具有快速建模能力的随机权神经网络为子模型.
随机权神经网络是由Pao和Takefuji于1992年提出的具有快速计算能力的人工神经网络[20–21].与传统基于梯度学习并需要通过误差反向传播迭代寻优的人工神经网络不同,RVFLNs算法是采用随机给定输入权值和偏置,以全局逼近理论为基础,采用Moore-Penrose广义逆矩阵方法一步求得输出权重.因此,该算法具有训练参数少、训练速度快等优点,其计算速度为传统BP–NN的数千倍.这样,为实际工业过程更快速的线软测量和在线控制奠定了基础[22].
给定M组集合(xi,yi),
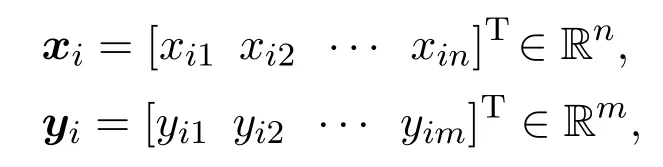
则带有L个隐层节点,以g(x)为激活函数的标准RVFLNs可以表示为

其中:OL,i(xi)为RVFLNs的输出值;wj∈,j=1,…,L为连接输入层与隐层的权值矩阵;βj为连接第j个隐含层节点与输出层神经元的输出权重向量;bj为第j个隐含层节点的偏置;

矩阵形式为

式中:
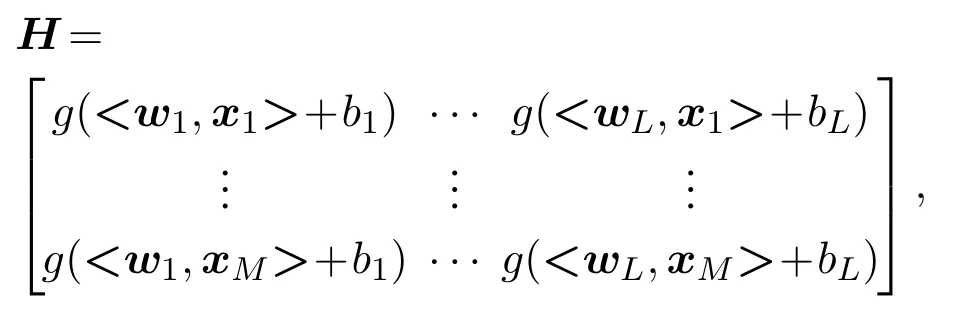

一般,训练样本个数要多于隐含节点个数,这样,H并不是方阵.于是式(9)方程组无解.此时,就需要采用最小二乘方法求解式(9)中方程组,结果如下:

式(10)中H†是由Moore-Penrose方法计算得到的H伪逆矩阵.
2)子模型模型结构的确立.考虑到常规的静态神经网络不能很好的反映高炉炼铁系统的大滞后、强耦合及复杂非线性动态特性,不能很好的包含高炉炼铁过程输入输出变量的时序及时滞关系,为了更好的反映高炉炼铁系统的复杂非线性特征,本文引入非线性自回归模型.假设多元铁水质量参数指标与高炉主体参数变量之间符合如下非线性关系[4]:
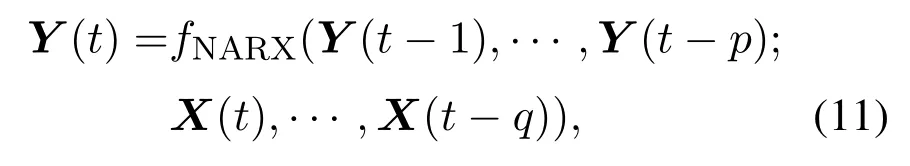
式中:X为建模输入变量集,Y为待估计的铁水质量指标集,p和q分别为过程输入输出变量的时序系数.本文采用我国柳钢2号高炉的本体数据与铁水质量数据(采样间隔为1 h)对所提方法进行数据测试.且取时序系数p=1和q=1.即将前一采样时刻的输入测量值X(t−1)以及前一采样时刻铁水质量指标值Y(t−1)连同当前采样时刻的输入测量值X(t)作为动态模型的综合输入.即建立的动态软测量模型用于实现的非线性动态映射关系为

3)所提算法的实现.对于N个子模型的权重分配问题,传统基于Bagging的集成模型一般把N分之一作为每个子模型的权重.这样,虽然在一定程度上能够提高系统的稳定性,但是,只是简单的把不好的欠拟合和过拟合的子模型以及真正好的子模型分配相同的比重,显然是存在一定的问题,并不是最优的权重分配方案.针对此点,本文提出一种均方根误差概率加权的思想进行子模型的权重分配.首先,利用核密度估计方法估计出N子模型的均方根误差集的概率密度函数曲线,然后,由得到的均方根误差概率密度函数曲线求解出每个子模型的概率,最后把各个子模型的概率作为自身的权重分配给每个子模型,进而进行加权求和得到最终的均方根误差概率加权集成RVFLNs模型[23].本文所提算法流程图如图3所示.

图3 所提建模算法流程图Fig.3 Flow chart of the proposed algorithm
由图3中的均方根误差概率密度曲线和均方根误差曲线分布可以看出,对于欠拟合和过拟合的子模型,本文所提方法会降低其所占有的比重,而真正好的子模型则会给出相应大分量的权值.这样,不仅可以提高集成模型的稳定性,还会使得模型的精度更高.所提算法具体实现步骤如下:
步骤1子样本集的产生.
进行基于Bootstrap思想的有放回抽样实验,对总体样本进行m次有放回随机采样实验,共进行N组,得到N个子样本集,且子样本集容量为m个.
步骤2子模型的选取.
为了提高集成模型的建模效率,一方面通过实验验证取得合适的子模型个数,另一方面选取具有快速建模速度的RVFLNs作为子模型进行建模.
步骤3求取每个子模型的均方根误差.计算每次子模型的RMSE公式如下:

其中:yji为第j个子模型中第i个输出变量的实际值,为第j个子模型中第i个输出变量的估计值,RMSEj为所求第j个子模型的均方根误差.
步骤4核密度估计方法的计算.
核密度估计(kernel density estimation,KDE)方法由Parzen首次提出,它是求解给定随机变量集合分布密度问题的非参数估计方法[24].其基本思想是假设xi∈,i=1,…,n为独立同分布随机变量,其所服从分布密度函数为f(x),x∈,则f(x)的核密度估计(x)定义为


本文选取高斯核函数,其表达式如下:
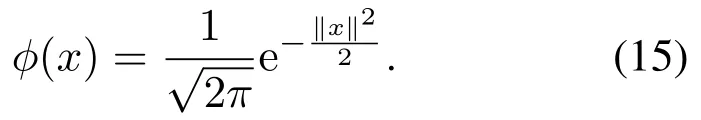
窗宽hp的选择对核函数的密度估计起着局部光滑的作用,如果hp过大会使模型误差PDF形状很光滑,使其主要部分的某些特征(如多峰性)被掩盖起来,从而增加估计量的偏差;若hp过小,则整个密度函数表现粗糙,尤其是在密度估计的尾部会出现较大干扰时[26].于是,窗宽hp选择设置为hp=1.06θ×其中θ由min{S,0.746Q}估计,S表示样本标准差,Q为4分位数间距,K为RMSE样本集个数.
步骤5均方根误差的概率计算.
利用核密度估计方法对于均方根误差样本集{RMSEi|i=1,2,…,K}进行PDF估计,得到均方根误差概率密度函数ΓRMSE如式(16)所示,然后根据均方根误差概率密度函数求解出每个子模型的均方根误差概率.
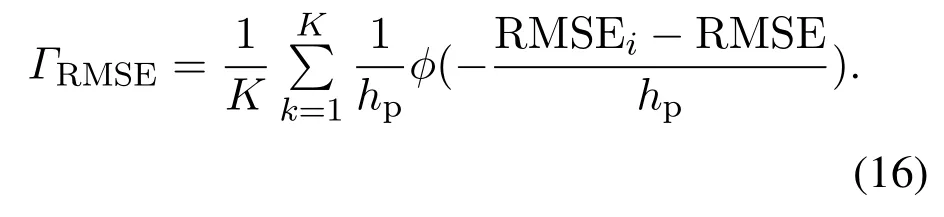
步骤6所提算法模型的求解.
均方根误差概率加权集成RVFLNs模型的求解如下:

其中:wi为在所提均方根概率加权思想下求得的权重,即由步骤5求得的每个子模型的概率作为自身的权重分配给每个子模型,且满足的条件为所有权重之和为1.代表每个子模型,N代表子模型的个数,而则为最终求得的均方根误差概率加权集成RVFLNs模型.
3 数值仿真验证
为了验证所提算法的有效性、优越性和普适性,进行如下数值仿真验证实验.考虑如下4输入4输出非线性系统:

式中:[t1,t2,t3,t4]为随机产生的400组在[−1,1]范围内的随机数,[e1,e2,e3,e4,e5,e6,e7,e8]为均值为0、方差为0.01的高斯噪声序列.
3.1 建模及效果
针对数学表达式(18)所述的非线性系统,选取输入的样本数据集为输出的样本数据集为=[y1y2y3y4],得到400输入输出数据集[].选取前300组作为训练数据集,用来训练均方根误差概率加权集成RVFLNs模型,选取后100组作为测试集,用来验证模型的预测拟合效果.按照第2.2节中本文所提算法的实现步骤1–6对式(18)中非线性系统进行建模.
其中:子模型的个数N为9,子样本集的容量m为300.使用核密度估计方法估计出均方根误差集的概率密度曲线如图4 所示,由均方根误差的概率密度曲线求解出表征每个子模型所占比重的均方根误差概率曲线如图5所示,所提建模算法的训练效果如图6所示.可以看出,本文所提算法得到的模型训练值能够很好的拟合式(18)非线性系统实际值的变化趋势,且能保证较高的精度.

图4 均方根误差的概率密度函数曲线图Fig.4 Probability density function curve of root mean square error

图5 均方根误差的概率分布曲线图Fig.5 Probability distribution curve of root mean square error
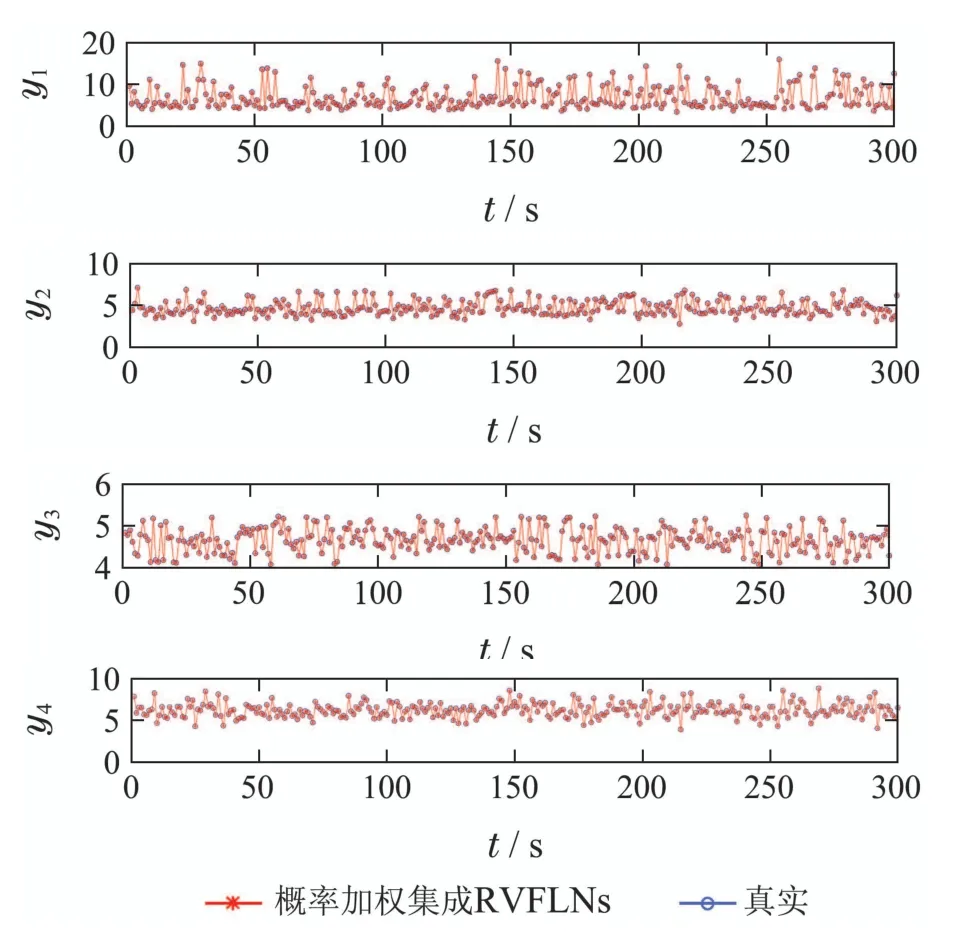
图6 所提方法建模效果图Fig.6 Modeling effect diagram of the proposed method
3.2 模型测试
为了验证所提算法的有效性和优越性,采用新的后100组测试集对模型进行测试.在设置同等条件下,分别对本文所提算法和RVFLNs算法进行对比实验.图7为两种算法下的测试跟踪曲线,从图7可以看出,在两种建模算法下,模型的预测值都能很好的跟踪真实值的变化,有较高的精度.但是,所提算法能够更好更精确的跟踪真实值曲线变化.
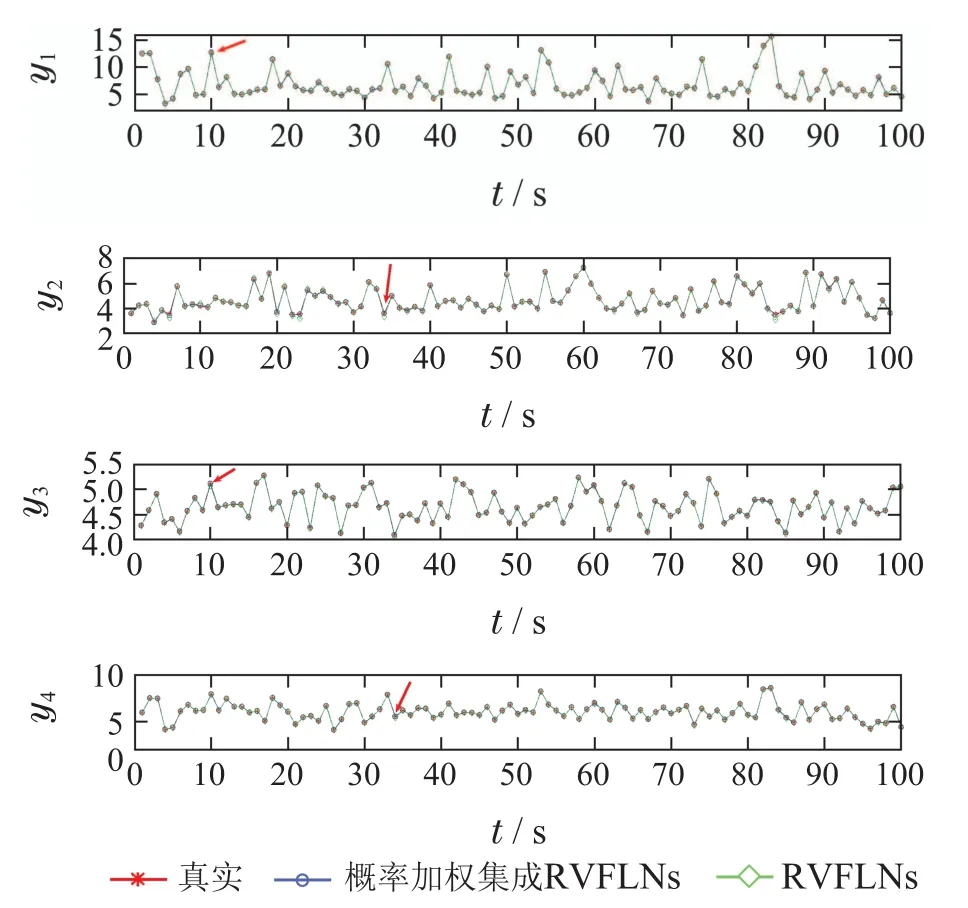
图7 不同建模方法下的预测效果对比图Fig.7 Comparison of prediction effects under different modeling methods
为了进一步说明所提算法拥有更高的精度,绘制两种算法下的建模误差PDF曲线如图8所示.从图8的PDF曲线图可以直观的看出所提算法的PDF曲线更加窄且高,建模误差以大概率集中在零均值附近.说明所提算法相比于RVFLNs算法拥有更好的跟踪真实值的性能和更高的预测精度.

图8 不同建模方法下的预测误差PDF曲线图Fig.8 Forecasting error PDF graph under different modeling methods
此外,表1列出了两种算法所建模型的均方根误差、命中率(%)两方面的统计指标.其中命中率(hit rate,HR)求取如式(19)所示,其中e0为绝对预测误差设定值.其中把y1∼y4的绝对预测误差分别设定为0.1,0.1,0.01,0.02.从表2中,可以看出,所提均方根误差概率加权集成RVFLNs算法相对于RVFLNs建模方法,拥有更小的RMSE和更高的命中率,进一步验证了所提算法的有效性和优越性.
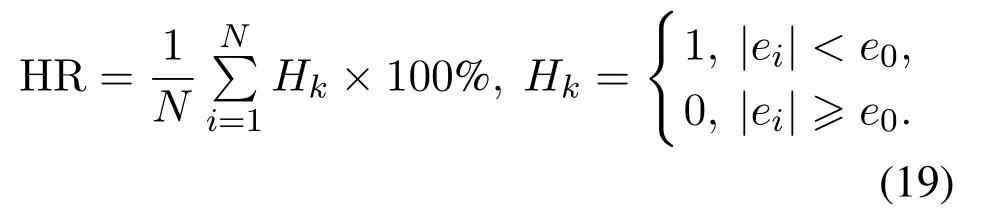
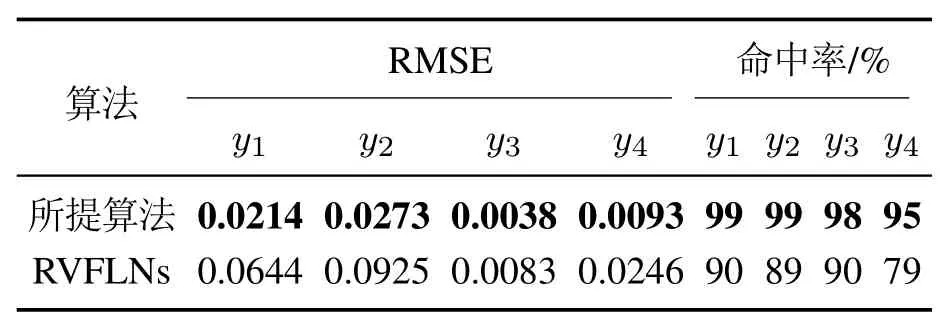
表1 不同建模算法相关统计指标比较Table 1 Comparison of statistical indicators related to different modeling algorithms
4 工业试验
4.1 数据的预处理及输入变量的选取
本文采用柳钢2号高炉的实际生产数据进行工业实验,建立多元铁水质量指标模型.为了提高建模数据质量,对高炉原始数据进行数据的预处理,具体做法包括对高炉本体原始数据进行时间粒度的统一、正常数据的筛选和数据的归一化等数据预处理操作.
针对高炉建模输入变量的选取,本文根据柳钢2号高炉炼铁工艺过程及相关仪器仪表的设置,确定影响多元铁水质量指标的19个关键过程变量为:冷风流量、送风比、热风压力、顶压、压差、顶压风量比、透气性、阻力系数、热风温度、富氧流量、富氧率、设定喷煤量、鼓风湿度、理论燃烧温度、标准风速、实际风速、鼓风动能、炉腹煤气量、炉腹煤气指数[1,4].考虑到影响高炉铁水质量的过程变量众多,并且各变量对铁水质量影响相差较大,若将其全部引入模型,一方面变量维数过高,导致模型训练时间延长和实时性差;另一方面过多的变量将引入较多的干扰,影响建模精度.为此,引入灰色关联分析法进行输入变量的选取.首先,用影响多元铁水质量指标的19个关键过程变量分别与作为输出变量的[Si](%)、[P](%)、[S](%)、铁水温度MIT(◦C)进行灰色关联度分析并计算出各自的关联度;然后,把这些关联度进行求和得到表2所示结果.最后,确定与铁水质量关联度最大的关键过程变量阻力系数x1顶压风量比x2、透气性x3、压差x4、鼓风动能x5、热风压力x6、实际风速x7为影响多元铁水质量指标的主要因素,并将这7个过程变量作为铁水质量模型的输入变量.

表2 灰色关联度分析结果Table 2 Gray correlation analysis results
4.2 建模及预测效果
将预处理得到的500组数据分为二个样本集D1,D2,其中:D1为训练样本集,用来训练并建立铁水质量模型,取前400组数据.D2为测试样本集,用来测试铁水质量模型,取剩下的后100组数据[3].按照第2.2节中本文所提算法的实现步骤1–6对铁水质量指标进行建模.
其中,子样本集的个数N为9,即子模型个数为9,子样本集的容量m为400.图9为核密度估计方法估计出的子模型的均方根误差的概率密度函数曲线,图10为每个子模型的均方根误差的概率分布曲线,图11为均方根误差概率加权集成RVFLNs建模算法的训练效果图,可以看出,本文所提算法得到的铁水质量指标模型的训练值能够很好的拟合实际值的变化趋势,且能保证较高的精度.
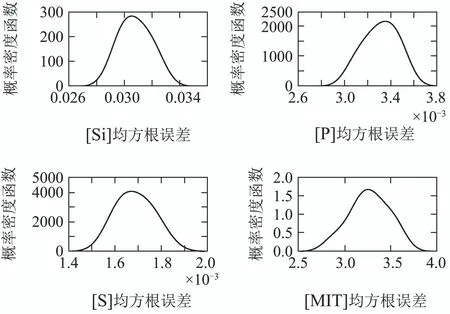
图9 均方根误差的概率密度函数曲线图Fig.9 Probability density function curve of root mean square error

图10 均方根误差的概率分布曲线图Fig.10 Probability distribution curve of root mean square error
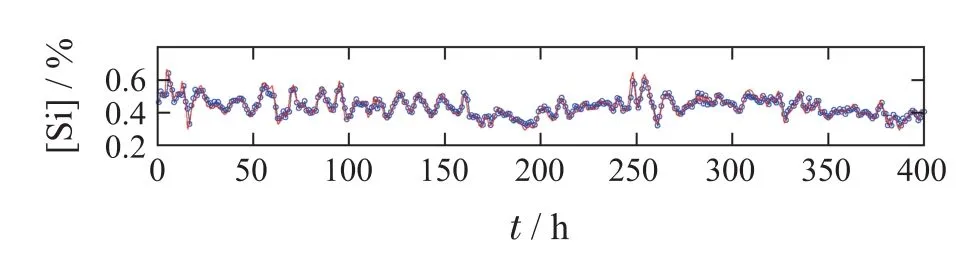
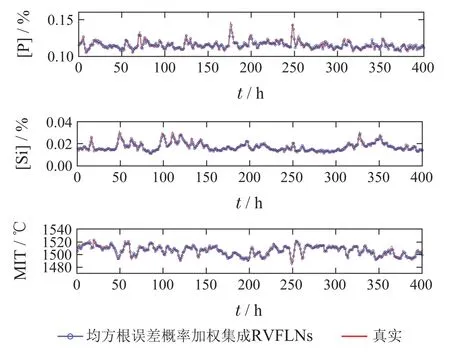
图11 所提方法铁水质量指标建模效果图Fig.11 Shows the method of modeling the quality of molten iron quality
采用新的后100组工业数据对模型进行测试,为此将本文所提建模算法与常见RVFLNs算法、BP神经网络(back propagation neural network,BP–NN)算法、多输出支持向量回归机(multi-output support vector regression,MSVR)算法进行多方面对比,相关模型参数选取如下所示:
1)RVFLNs算法隐含层节点和输出层节点的传输函数分别选取Sigmod函数和线性purelin函数,隐含节点数选取为30.
2)为了不失一般性,对本文所提算法也设置和RVFLNs算法同样的条件.即隐含层节点和输出层节点的传输函数分别选取Sigmod函数和线性purelin函数,隐含节点数选取为30.
3)同理,对BP–NN算法隐含层节点和输出层节点的传输函数也分别选取Sigmod函数和线性purelin函数,隐含节点数选取为30.
4)MSVR激活函数选为Sigmod函数.另外有,MSVR中的惩罚因子C表示对误差的容忍度,而核函数参数σ表示所选的支持向量的影响范围.这里采用交叉验证法将其分别确定为C=1和σ=0.01.
图12为不同建模方法下的多元铁水质量指标的预测效果图.可以看出MSVR算法拟合值不能很好的跟踪实际值的变化趋势,模型的预测精度最差.而RVFLNs和BP–NN模型输出的预测值基本能后跟踪实际值的变化趋势,但是模型的预测误差较大,精度还有待提高.相对而言,本文所提算法下的多元铁水质量模型的预测精度最高,其模型预测值能够准确的跟踪实际值的变化趋势,模型预测效果最好.
为了进一步说明这一问题,并刻画具有随机特性的建模预测误差更多的统计信息,引入概率密度函数对建模预测误差的二维空间分布情况进行评价.图13为不同建模方法下的预测误差PDF曲线图,从图13显示的信息,可以看出,相对于其他建模算法,本文所提算法的预测误差PDF曲线更加高且窄,更加接近零均值高斯分布的白色噪声.从而进一步验证了本文所提算法的有效性和优越性.
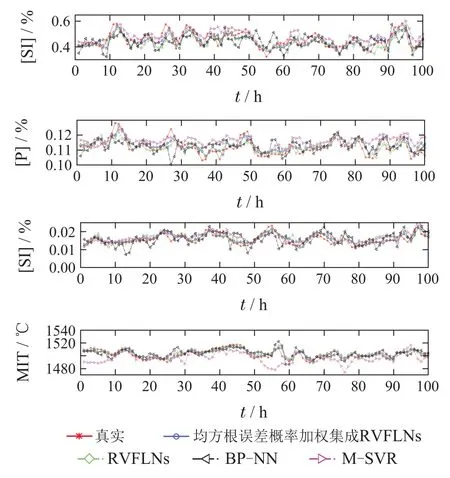
图12 不同建模方法下的铁水质量指标预测效果对比图Fig.12 Comparison of prediction results of hot metal quality indicators under different modeling methods
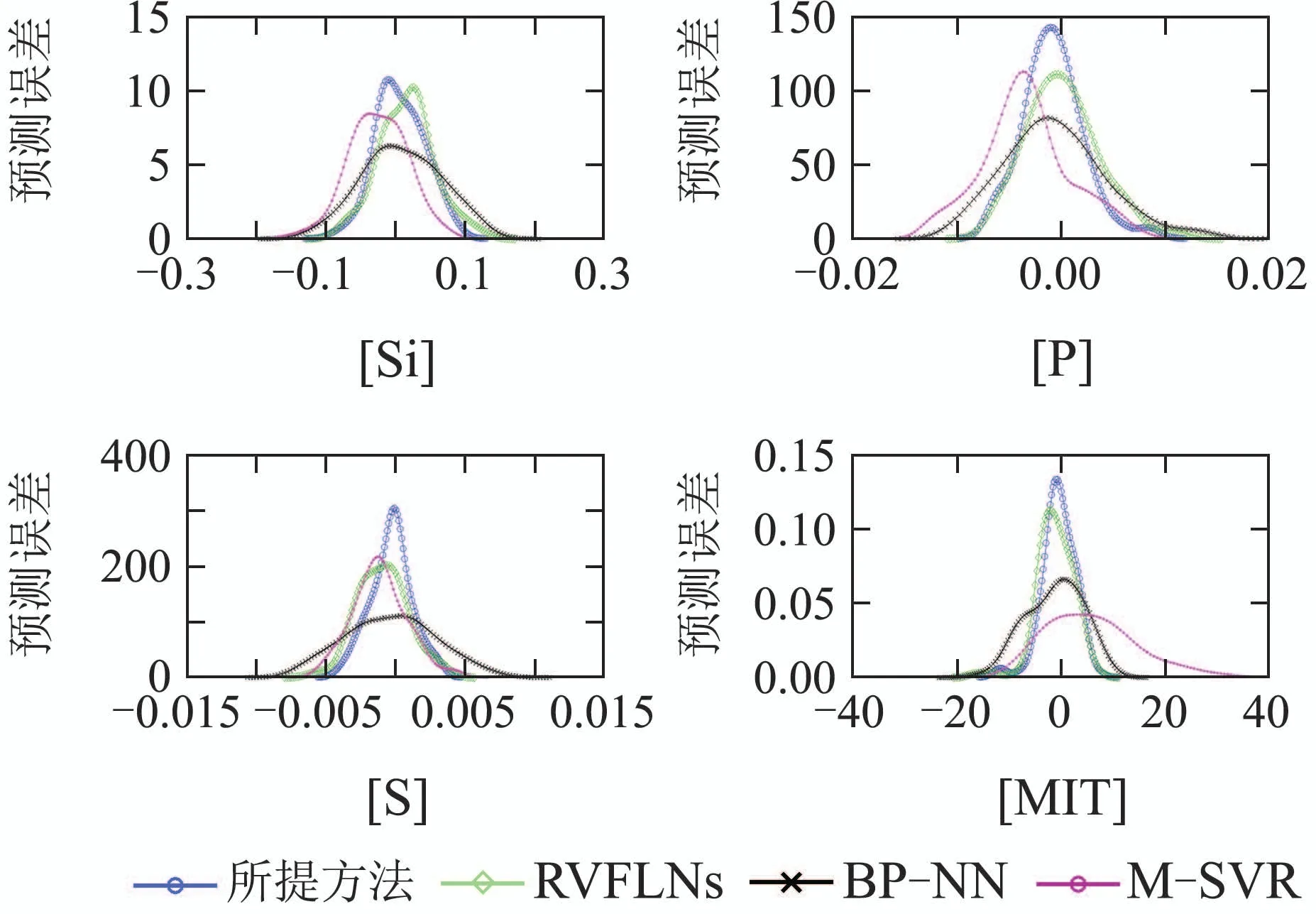
图13 不同建模方法下的预测误差PDF曲线图Fig.13 Prediction error PDF graph under different modeling methods
此外,本文实验运行在64位Windows 7操作系统,i7–3770,3.40 GHz的4核CPU,且内存为8 GB的电脑上,表3列出了不同算法所建模型的运行时间(s)、均方根误差、命中率(%)3方面的统计指标.结合实际工程应用的指标精度,并把[Si]、[P]、[S]、MIT绝对预测误差设定为0.1,0.006,0.003,5.从表3中,可得在运行时间上,所提算法仅比RVFLNs算法多出0.0074 s,但是要远优于MSVR算法和BP–NN算法,尤其是BP–NN算法,提高了近400倍的速度,可知所提算法有更高的建模效率.在RMSE和命中率上,本文所提算法相对于其他建模方法,拥有更小的RMSE和更高的命中率.综合以上分析,本文所提算法能够很好的预测多元铁水质量指标的变化趋势,拟合精度高、建模速度快、算法简单且易于工程实现和工业应用.
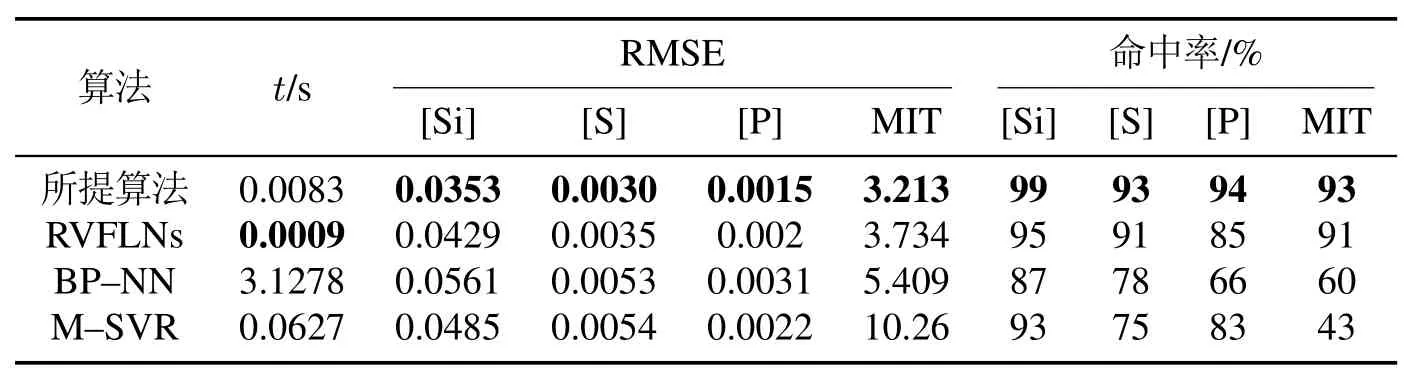
表3 不同建模算法相关统计指标比较Table 3 Comparison of statistical indicators related to different modeling algorithms
5 结论
本文结合高炉炼铁的实际过程,旨在建立一种建模快速、精度较高且易于工程实现的高炉多元铁水质量指标预测模型,主要工作包括:1)为了提高建模数据的质量,对高炉实际数据进行预处理,从而得到高质量的高炉建模数据;2)为了提高建模效率和降低计算复杂度,采取灰色关联分析法,从影响多元铁水质量指标的19个关键过程变量中提取与之关联度最强的7过程变量作为建模输入变量;3)为了更好的反映高炉炼铁的非线性动态特性,引入NARX模型;4)为了提高建模的精度,提出一种均方根误差概率加权集成RVFLNs算法,用于建立基于数据驱动的多元铁水质量预测模型.数值仿真验证、工业实验及对比分析表明:所提算法具有更高的预测精度,能够根据高炉炼铁过程实时输入数据的变化,实现对多元铁水质量进行快速准确的预测.
