加性噪声下网络化多输入离散系统均方可镇定
2020-06-11陈军勇沈志萍邬依林
陈军勇 ,沈志萍 ,邬依林
(1.浙江科技学院信息与电子工程学院,浙江杭州 310023;2.河南师范大学数学与信息科学学院,河南新乡 453007;3.广东第二师范学院计算机科学系,广东广州 510310)
1 引言
网络化控制系统(networked control system,NCSs)是系统和控制器通过共享网络进行通信的反馈控制系统,近年引起了极大的关注.该系统广泛应用于移动传感器网络、高速公路系统和多智能体系统等[1–3].很多期刊和会议都对该主题进行过专题讨论,例如文献[4–8]等.
网络化控制的一个基本问题是输入信道信息约束下的可镇定性.研究中常常采用很多不同形式的信息约束,例如数据率约束[9–10]、量化[11–12]、丢包[13–15]、量化与丢包[16]、信噪比受限[17–18]、时滞[19–20]等.利用对数量化器量化输入信号,文献[21]讨论了多输入系统状态反馈均方可镇定问题.基于李雅普诺夫方法,得到系统二次可镇定下最粗糙量化密度要求,该要求可用系统的米勒测度表示,即不稳定极点的乘积.文献[13]研究发现基于乘性随机输入信道下网络化系统状态反馈均方可镇定的充要条件是乘性信道的均方容量超过系统的拓扑熵,即米勒测度的对数.这些结果揭示了米勒测度或拓扑熵的重要作用,可以视为开环系统不稳定度的一个度量.文献[22]通过数据率约束信道及系统拓扑熵研究了可观测性和最优控制之间的联系,该结论进一步支持了上述观点.
对于多输入系统的网络化镇定问题较单输入系统的研究变得更加复杂,网络化多输出系统状态反馈均方可镇定时的最小网络要求条件很难得到.幸好,文献[23–27]取得了很大的进展.例如,基于信噪比受限下独立平行信道,文献[26–27]讨论了离散时间多输入多输出系统均方可镇定问题,给出系统均方可镇定的充分必要条件,该条件涉及到不稳定极点的值及其方向.最近,一系列研究利用信道资源分配的思想来探寻可镇定性的最小信息要求.凭借因信道资源可分配而产生的额外设计自由度,已经证明多输入网络化可镇定性所需的最小总容量可由开环系统拓扑熵刻画.另一种方法是每个信道资源固定,而从通信理论角度借助于多输入多输出传输机制,讨论网络化可镇定的问题,文献[28]借助此思想,基于优化序方法给出加性噪声信道下均方可镇定的充分必要条件.类似的方法被推广到乘性噪声信道及更一般信道下网络化可镇定[21,29].
受网络化系统均方可镇定的启发,尤其是文献[21,28–29]中思想的启发,本文借助相应的思想建立网络化离散系统均方可镇定与系统不稳定度的联系,特别是借助优化序思想来给出信道资源不能任意分配时系统均方可镇定的充分必要条件.与文献[28]和文献[21,29]不同之处有3点:1)本文主要讨论的是离散时间系统下的均方可镇定;2)信道容量定义不同;3)因解决不同的问题,所得结论截然不同.
为解决信息受限下多输出网络化系统均方可镇定问题,本文的特色:当信道资源不能分配,利用编码和解码矩阵将问题转化成编码和控制器联合设计问题.为达到均方可镇定,编码和控制器要适当设计.本文给出用优化序表示的充分和必要条件,表明最小网络要求与循环分解子系统的米勒测度有紧密联系.
值得指出的是,不管是信道/控制器联合设计还是编码/控制器联合设计问题,都可看成是通信资源供需平衡问题.控制一个网络化系统,每一个输入需要一定数量的通信资源.供需平衡可以通过两方面不同设计.信道/控制器联合设计是调节供应来满足需求,而编码/控制器联合设计则相反,即调节需要来满足供应.
2 问题描述
考虑如图1所示网络化系统,其中离散时间多输入线性时不变系统描述为
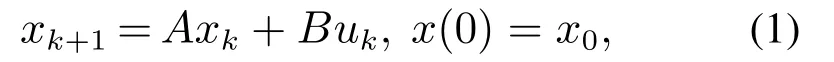
其中:xk为系统状态;uk是控制输入;假设(A,B)不稳定但可镇定.设状态xk可用来做状态反馈.如果控制器和系统之间的通信网络是理想的,即uk=vk,则容易设计状态反馈控制器vk=Fxk使得闭环系统稳定.然而,当通信网络不是理想的,即uk为vk的失真后的信息,因系统可镇定性依赖于通信网络传输精度,该状态反馈设计将面临着新的问题.
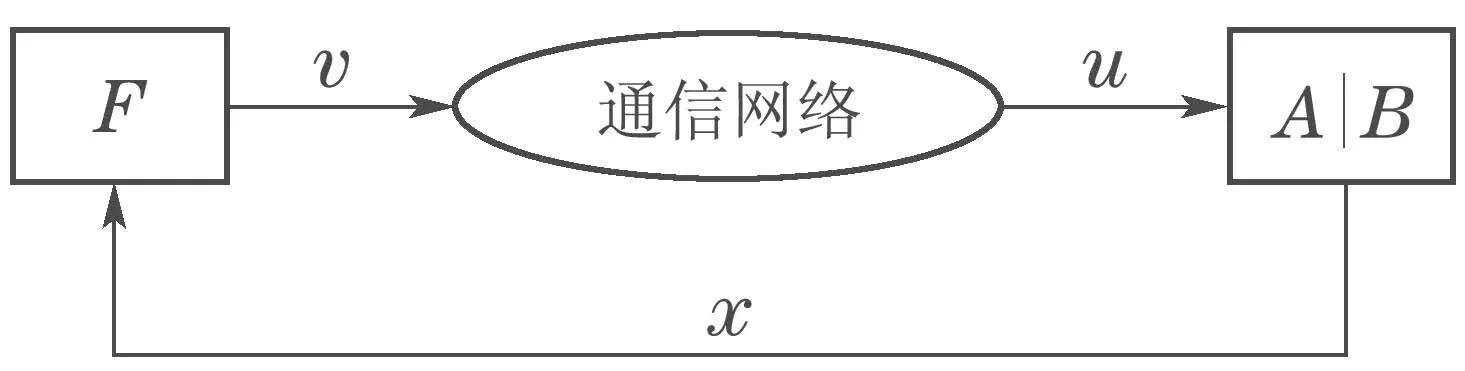
图1 网络化反馈控制系统结构图Fig.1 State feedback via communication network
文献[15,30]借用网络资源可分配的思想讨论了多输入网络化系统均方可镇定时的最小信道容量,但该讨论基于总的资源可在任意平行信道中分配的假设.如果总的资源是不能分配的,该问题面临着新的挑战.针对这一问题,本文针对离散时间多输入网络化线性系统,借助于编码控制联合设计思想来解决这一问题.即将通信网络建模为一编码矩阵T,加性高斯白噪声平行信道和一解码矩阵R,如图2所示.
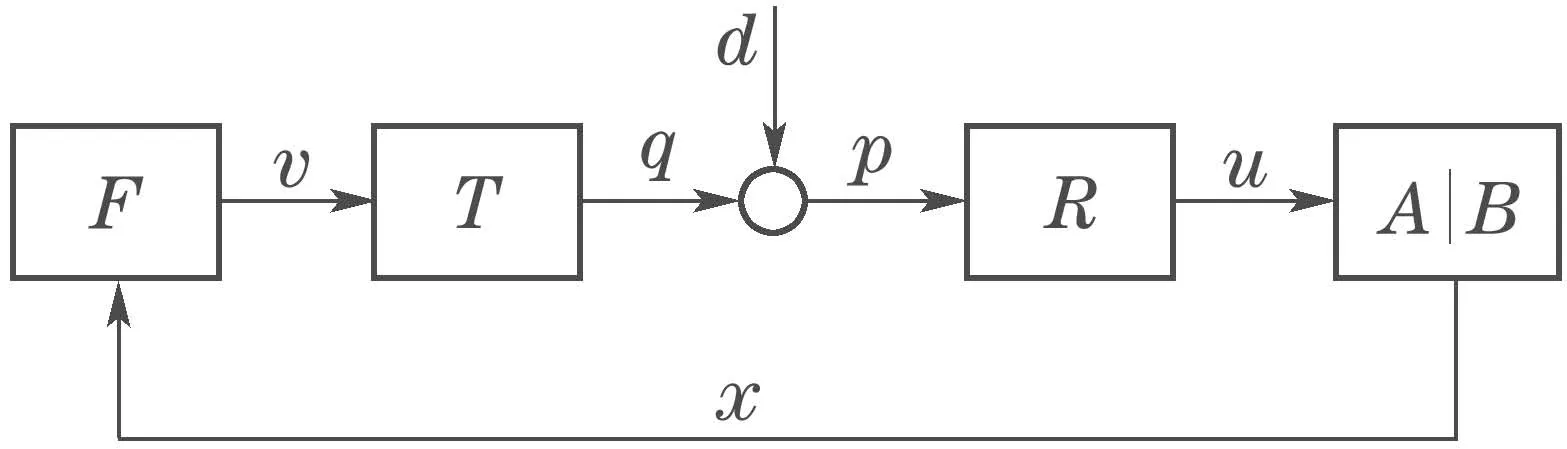
图2 加性高斯白噪声及编码解码信道Fig.2 Communication channels with encoding and decoding
信道描述:通信信道建模成加性白高斯噪声,信道输入信号qi是具有容许功率Pi的静态过程,即

信号传输被具有零均值功率谱密度为Ni的白高斯噪声干扰.比值称为信噪比,记为SNRi.本文考虑无限带宽加性高斯白噪声这一理想情况.该高斯白噪声信道容量定义为[30]
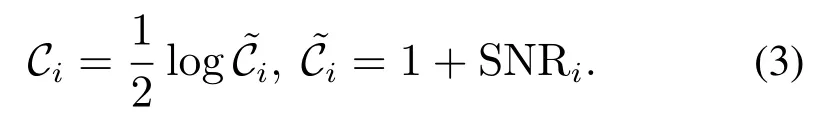
总的信道容量为C=C1+C2+…+Cl.因提前设定容许功率,则信道容量是固定的且不能任意分配与资源可任意分配[15,30]相反.然而,编码解码矩阵的设计可以代替资源不可分配产生的设计局限.特别的,假设编码和解码矩阵受以下约束:

问题提出:当网络资源不可任意分配时,如何实现网络化离散时间系统可镇定? 本文的目的有两个:1)联合设计编码控制使得可镇定可以实现;2)网络化系统均方可镇定时各信道容量与系统拓扑熵需满足什么关系?
3 预备知识
本节给出一些基本知识,包括H2补灵敏度、循环分解和优化序理论等.
循环分解:一般来说,对于任意方阵,总能进行如下循环分解:
引理1[31]对每个可镇定线性系统[A,B],其中则存在非奇异矩阵P和Q使得
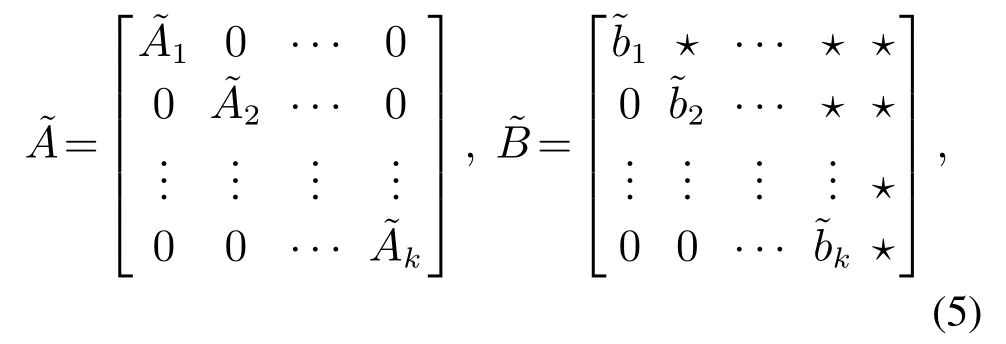
优化序理论:一些有用的引理如下:
引理2[32]优化序不等式成立,等价于存在一向量z使得xz(x>z),且
上述引理刻画了优化序和弱优化序之间的关系.
引理3[32]存在具有特征值λ1,λ2,…,λn和对角元素d1,d2,…,dn的实对称矩阵X的充分必要条件是
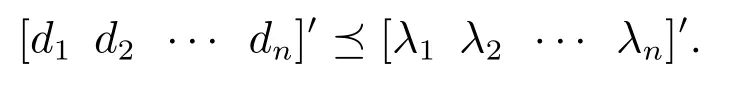
当引理3中条件满足,有很多方法计算期望实矩阵X,可参考文献[33],更多关于优化序知识可参考文献[32].
最优补灵敏度:考虑图2所示网络化系统,假设信道暂时是理想的,则系统的补灵敏度函数(从信道噪声dk到信道输入qk的传递函数)为

引理4[30]假设(A,B)可镇定,则有
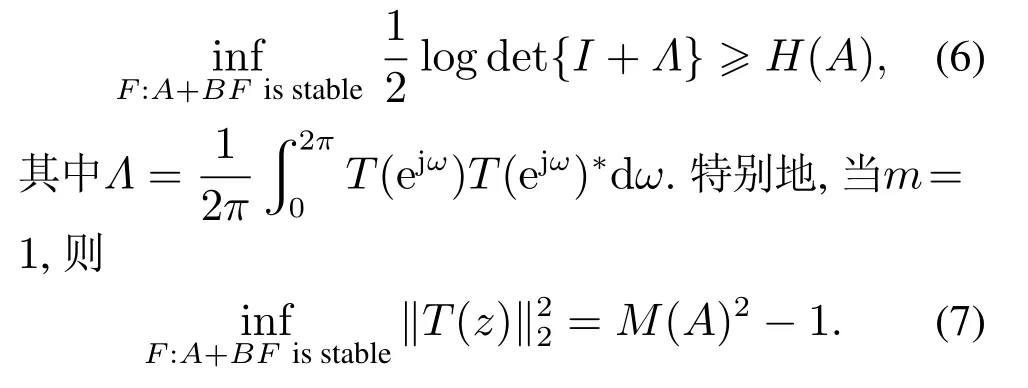
对于单输入情形,即m=1,可参考文献[34].
4 主要结论
现有很多文献主要考虑了总的资源可分配到各平行信道中,实际上是调节供应以满足需求.然而,有时可能会碰见诸如网络设备提前分配但不能任意分配的情况,此种情况下,各个信道资源Ci提前给定但不能分配.接下来的问题是能否借助其它设计方式来补偿资源分配的缺失.答案是明确的,可借助设计传输/接收矩阵T和R,进而控制器设计问题转化成控制器和传输联合设计问题.给出主要结论前,我们从供需平衡角度来分析传输器设计机制.因为每个信道的信道容量提前固定,即供应方不能再操作.而利用合适的线性传输矩阵T,每个信道传输所有输入的信号线性组合信号,实际上是调节了信道需求以满足供应.这刚好是现有方法的反面.
本节主要考虑信道模型为加性白高斯噪声下,讨论存在合适的编码解码矩阵T和R以及反馈控制增益矩阵F使得闭环网络化系统内部稳定(所有信号的分布指数趋于静态分布)的充分必要条件.根据系统模型,总的噪声d=[d1d2… dl]′为白高斯噪声向量,其功率谱密度为N=diag{N1,N2,…,Nl}.补灵敏度函数(从信道噪声dk到信道输入qk的传递函数)为
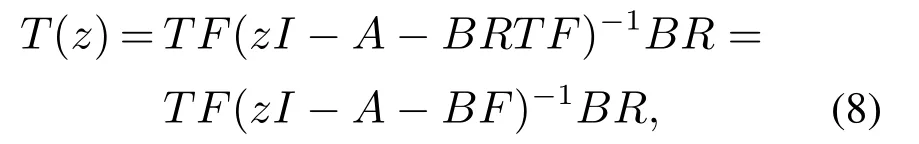
则qi的功率谱密度为{T(ejw)NT(ejw)∗},进而qi的功率可表示为
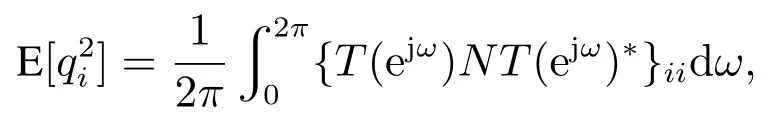
其中{·}ii表示矩阵的第i个对角元素.因此,输入功率受限(2)可转化为

考虑到式(3),此约束可进一步转化为
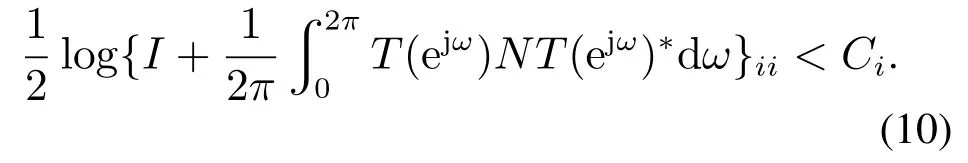
本节的目的是找到对信道容量Ci(i=1,2,…,l)的要求,通过联合设计编码/控制使得网络化系统在约束条件(2)下达到网络化可镇定.同时也提出一个编码/控制协同设计的程序.
为了镇定网络化控制系统,每个控制输入要求一定通信资源用来传输.因此,控制输入可看成通信资源的需求方,而通道可看成供应方.通道的供应容量由其信道容量刻画.问题是信道容量提前给定,一般情况下供需不一定平衡.为解决这种供需不平衡,引入编码矩阵T,用来从不同的控制输入产生混合输入需求.考虑到这一点,一个有趣的想法是合理利用编码机制,以便在混合之后,需求将被合适地重新塑造以匹配供应.与文献[15,30]中采用的信道资源分配完全相反,即调节供应以满足需求.请注意,需求塑造是经济学中非常普遍的原则.它在工程领域也引发了许多成功的故事,如电力系统[35]、交通运输[36]和数据网络[37]等.
接下来作者将利用弱优化序关系解决编码/控制协同设计问题,给出一个充分条件和一个必要条件.
定理1基于高斯白噪声信道下的网络化系统,通过编码控制联合设计均方可镇定的充分条件是
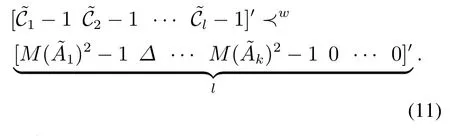
必要条件为
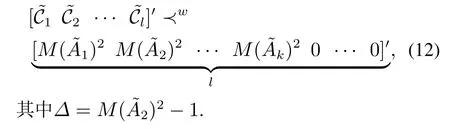
证为简洁起见,假设A的所有特征根在单位环外.该假设合理性可参考文献[15,30].
首先证必要条件(12)成立:注意到信道总可以重新排列使得其信道容量按非增次序.因此,不失一般性,假设各信道容量关系如下,即非增顺序
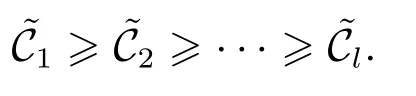
假设存在一状态反馈增益F和一对传输接收矩阵{T,R}使得网络化系统在信噪比约束下是均方稳定的.
根据引理1中的关系αi+1(λ)|αi(λ),易知的谱总包含于的谱,因此不等式
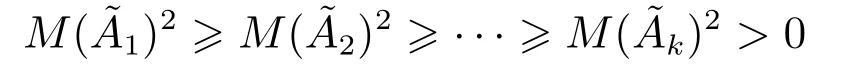
恒成立.优化序(12)等价于下列不等式:
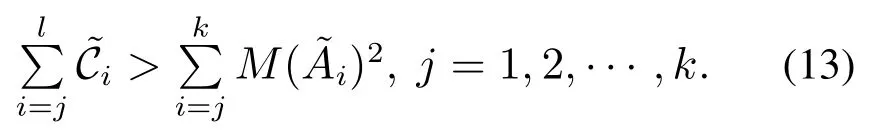
由文献[30]定理3,信噪比约束的均方可镇定表明总的信道资源要大于系统开环拓扑熵,即
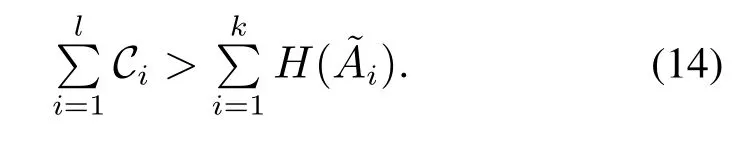
不等式(14)可写成如下对数形式:

对式(15)进行变形并取指数函数得
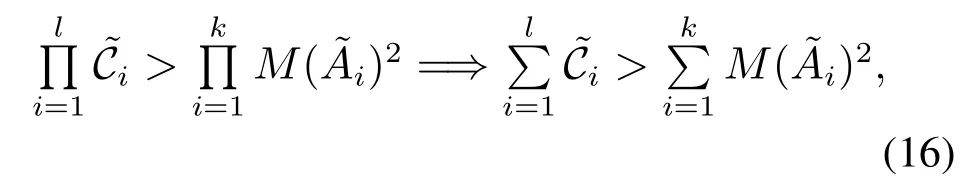
为了讨论j=2情形,本文首先对系统[A|BR]中关于BR的第1列进行能控性分解.换句话说,存在一个非奇异矩阵和一个状态变换zk=P−1xk使得辅助系统的动态方程变为

对上述方程取拉普拉斯变换,有

其中:
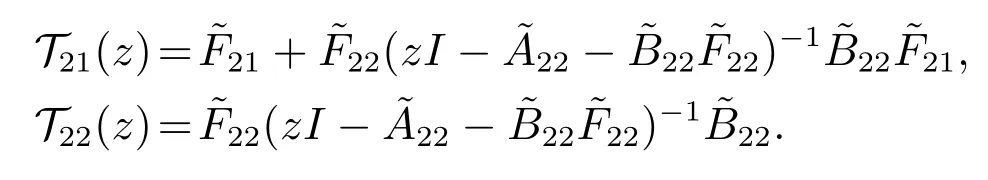

上述方程两边同时求和,可得
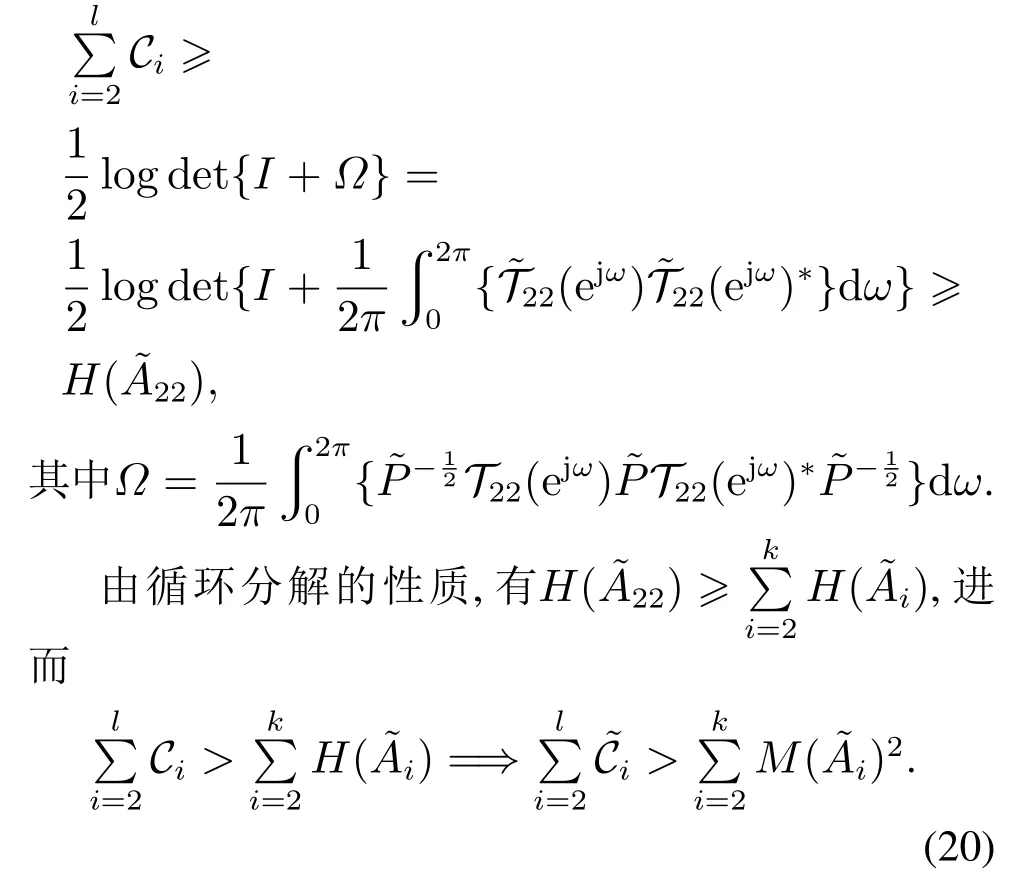
模仿上述的过程,很容易验证当j=3,4,…,k时,式(13)也成立.必要条件(12)得证.
其次证明充分条件(11)成立:为证充分条件(12)成立,需设计一传输矩阵T,一个接收矩阵R和一状态反馈增益矩阵F,使得闭环系统达到信噪比约束下均方稳定.不失一般性,假设[A|B]已是循环分解形式,其中每个循环子系统是维数为ni的可镇定系统.对每个子系统可设计状态反馈增益为使得其中
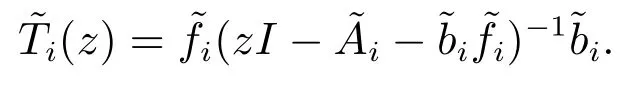
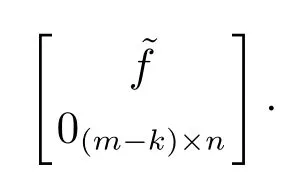
由此,A+BF是稳定的.特别地,设传输和接收矩阵为
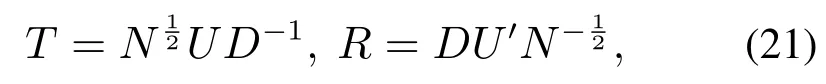
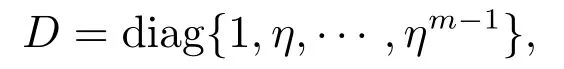
η是一正的小实数.令
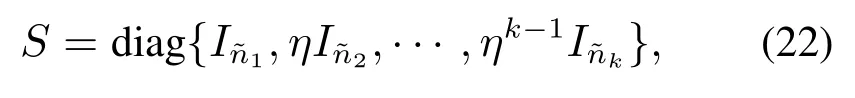
则有
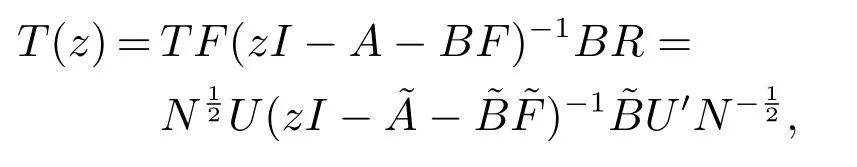
其中

类似式(10),有
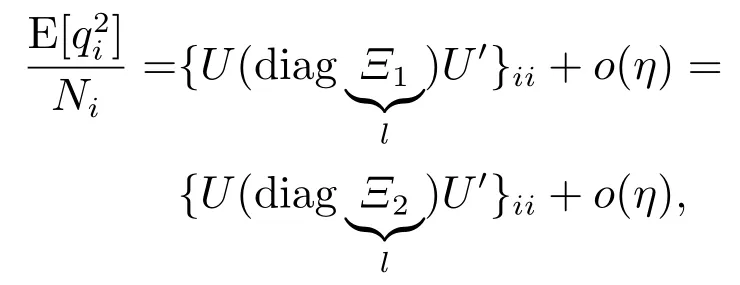
其中:
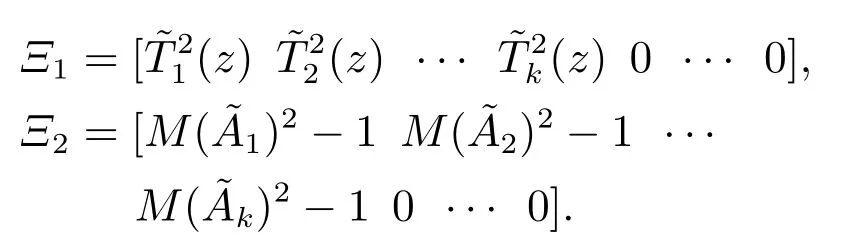

由引理3,总可构造一酉矩阵U使得
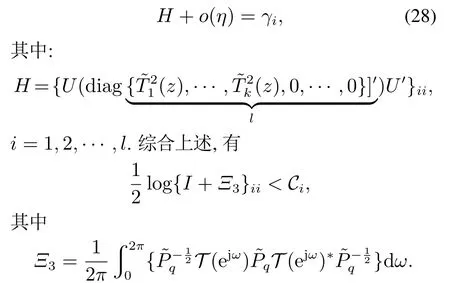
当η取足够小的实数,有即信噪比约束满足,充分条件(11)得证. 证毕.
注1从弱优化条件(11)–(12),可以推断,在某些情况下,甚至可以用比控制输入数量少的通道来镇定网络化控制系统.实际上,镇定所需的最小通道数等于从循环分解(5)得到的不稳定循环子系统的数量.这与文献中的早期研究[38]镇定线性系统所需的最小控制输入数量一致.
注2由充分性条件式(11)和必要性条件式(12)可以看出,若充分性条件成立,则必要性条件一定成立,但反之未必成立.当系统循环子系统个数与信道个数一致时,弱优化条件(11)–(12)一致,即充要条件,见下面推论1–2.
由定理1,进一步可推导如下两个推论:
推论1如果循环分解(A,B)有l个不稳定循环子系统,则基于加性白高斯噪声信道的网络化系统(A,B),可通过编码控制联合设计可镇定的充分必要条件为

证当(A,B)有l个不稳定循环分解系统,弱优化条件(11)–(12)分别变为
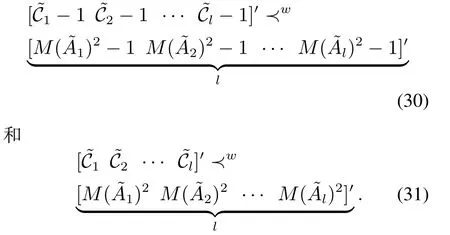
则由优化序性质式(30)等价于式(31),即充分和必要条件一致. 证毕.
易知,当l=1时,即系统只有一个传输信道,也就没有信道分配问题了,该结论与文献[30]中结论一致,要求总容量大于系统开环拓扑熵,与如何分配各个渠道的能力是不相关的.
推论2如果循环分解(A,B)有l个不稳定循环子系统,且则基于加性白高斯噪声信道的网络化系统(A,B),可通过编码控制联合设计可镇定的充分必要条件为
证当弱优化条件(11)–(12)分别变为

则此充分必要条件即为
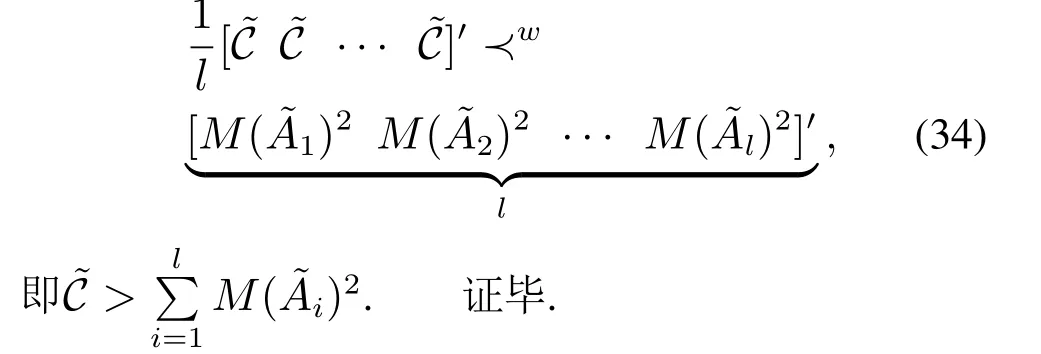
推论2表明,相同容量的通信信道可以很好地帮助彼此传输信号.同时,当l=1时,即系统只有一个输入信道,该结论与文献[30]中结论一致,要求总容量大于系统开环拓扑熵.
5 仿真研究
本节中,给出一个数值示例来说明如何通过通道控制器协同设计来镇定网络化控制系统.考虑一个不稳定的系统[A|B]:
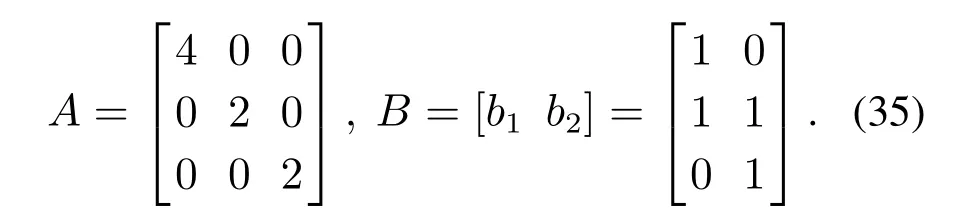
初始条件x0=[1 1 1]′.显然,[A|B]可镇定.进一步[A|B]已是循环分解形式,循环子系统为
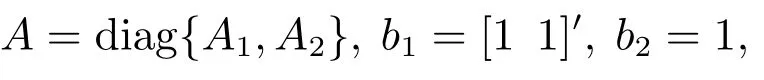
其中A1=diag{4,2}和A2=2.系统的拓扑熵为

对于控制器设计问题,通过求解两个子系统[A1b1]和[A2b2]的H2最优补灵敏度函数T(z)来获得f1=[−6.5625 1.3125]和f2=−1.5.令
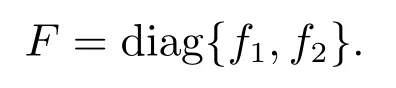
至于编码器设计问题,尽管C1 因此,由定理1,系统可联合设计编码控制器,取γ1=48和γ2=20,使得 显然,当选择合适的足够小的正数η=0.001,U为酉矩阵,且下面矩阵对角元素趋于γ1和γ2: 进一步,编码解码矩阵设计为 至此,完成设计过程.利用Simulation工具仿真,状态协方差阵的Frobenius范数为 根据以上结果,可得闭环系统是均方稳定的,同时,计 本文研究了离散时间网络化控制系统的可镇定问题.信道模型为加性白高斯噪声,用于描述通信过程中的信号失真,且信道资源提前固定不可任意分配.通过优化序理论及线性系统中能控性理论,结合编码与控制联合设计思想,用优化序形式给出网络化系统均方可镇定的充分和必要条件,此条件建立了系统均方可镇定与系统拓扑熵之间的关系,同时也给出设计程序.最后,给出一个数值例子来验证结果的有效性.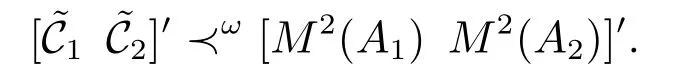

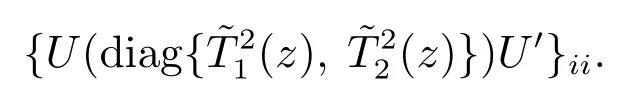
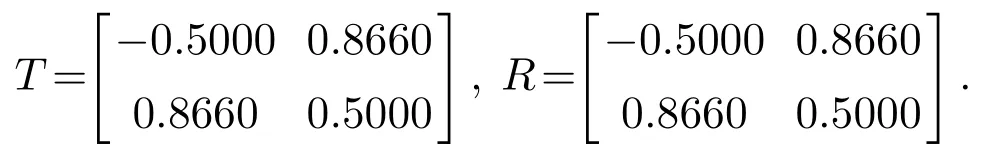
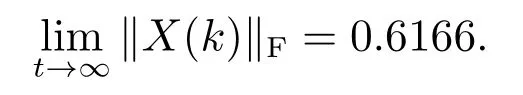
6 结论
