采用CIC的FRM滤波器的System generator实现∗

（上海船舶电子设备研究所 上海 201108）

1 引言

FRM技术是目前设计窄过渡带滤波器应用较广的一种技术，可设计任意带宽的窄过渡带滤波器，且复杂度较低，目前国内外对其的研究主要集中在结构优化设计［1～5］、相关算法［6］、应用领域以及相应的硬件实现方面［7～8］，其目的是降低实现的复杂度以及相应的工程应用。在结构优化方面一般是对原型滤波器和屏蔽滤波器进行优化设计，目前在减少FRM滤波器复杂度方面可做的工作不多，多集中在应用与硬件实现方面。

由于CIC滤波器的结构简单，没有乘法器、只有加法器、积分器和寄存器，只需将相邻的数据相加即可得到输出数据［9］，适合于工作在高采样率条件下，具有运算速度快，占用资源少的特点，因此可以将CIC滤波器应用于FRM滤波器中，作为屏蔽滤波器，进一步降低FRM滤波器所需乘法器的数量，进而降低了复杂度，且CIC多应用在窄过渡带低通FRM滤波器中。

System generator［10～12］是 Xilinx 公司推出的 DSP设计开发工具，通过在Matlab的Simulink环境中搭建模型，然后调用System generator自动将Simulink模型转换成FPGA可执行的模型，直接生成FPGA可执行的代码，然后经过综合、仿真以及相应芯片的配置后下载到硬件环境中进行测试。

本文通过使用ISE软件中的System generator工具库，结合Matlab/Simulink库搭建相应的模块来验证采用CIC的FRM低通滤波器设计方法的硬件可实现性，通过对采用多级内插和多级抽取CIC构成的FRM低通滤波器进行分析，并与传统的FRM低通滤波器进行对比，说明了多级内插积分梳状滤波器在FRM低通滤波器设计中的有效性。

2 频率响应屏蔽技术（FRM）

频率响应屏蔽技术［2］（Frequency Response Masking，FRM）是设计窄过渡带滤波器最常用的方法。通过使用原型滤波器和与其幅度互补的滤波器来产生任意带宽的窄过渡带滤波器，且相对于传统的方法，FRN技术减少了乘法器的使用，进而降低了硬件资源的复杂度，所以近年来对其的应用与研究较多，其基本一级结构如图1所示。

图1 FRM滤波器的基本结构

FRM滤波器的结构包括原型滤波器以及和它幅度互补的滤波器和两个屏蔽滤波器，通过进行内插得到过渡带较窄的滤波器，M为内插因子，屏蔽滤波器的作用是去除原型滤波器内插引起的多余周期子带。原型滤波器和两个屏蔽滤波器的传输函数如下：

其基本的传输函数为

其滤波过程原理如图2所示。图中M表示内插因子，θ和φ分别为滤波器的通带截止频率和阻带截止频率，m为一个整数。图（a）和图（b）分别表示FRM滤波器形成的两种情况。图（a）表示由插值后的原型滤波器提供过渡带的情况，图（b）表示由插值后原型滤波器的互补滤波器提供过渡带的情况，两种方法产生的过渡带宽度一样，但是各个滤波器的通带宽度不一样，而且每个滤波器中的子滤波器的阶数也不一样，所以产生的目标滤波器的复杂度也不一样。通过将以上参数代入不同的表达式来计算以上两种情况下的各个子滤波器的截止频率，使其达到最优，满足所设计的低复杂度滤波器的要求。

图2 FRM滤波器设计原理图

3 积分梳状滤波器（CIC）

积分梳状滤波器一般是用来完成抗混叠（或去镜像）滤波的［5］，它的冲激响应函数为

（R为FIR滤波器的长度）

从滤波器的冲激响应可以看出，CIC滤波器是一种具有线性相位的FIR滤波器，当通过卷积和来计算输出信号时，可以看出其滤波计算只有加法而没有乘法，只需将相邻的数据相加即可得到输出数据，卷积公式为

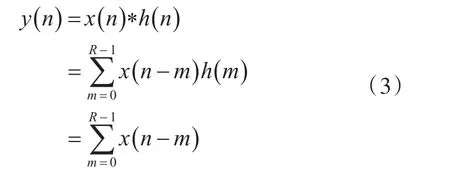
由此可以看出积分梳状滤波器不仅可以节省硬件资源，而且减少了运算时间。因此将CIC应用在FRM滤波器中可以进一步降低复杂度，其结构图如图3所示。

图3 采用CIC的FRM滤波器

4 FRM滤波器的设计

System generator［7～9］是 Xilinx 公 司开发 的系 统级DSP设计建模工具，通过在Simulink环境下，调用Xilinx的工具包，搭建系统模型，完成Simulink功能仿真，同时转换成硬件可执行模型，直接生成用户需要的FPGA代码和比特流文件，ISE可以对整个工程文件进行综合、仿真、布局布线和优化设计等，完成芯片配置后可以下载到相应的硬件环境进行测试（或直接调用System generator的硬件协仿真功能进行在线测试），并能将结果反馈到Simulink环境中，提高了设计的灵活性和效率，降低了数字信号处理的设计人员的工作难度。

System generator和Matlab的Simulink是无缝连接的，能自动将数字系统设计的系统级模型转换为用户需要的硬件描述语言，并能直接完成板上测试，所以在数字信号处理领域得到了广泛的应用。FRM滤波器实质上可以看成是一个滤波器组，通过各个滤波器的级联来达到最终的目的，因此为了在硬件上测试FRM滤波器的性能，可以选择使用System generator对本文提出的方法的进行硬件设计，通过调用相应的模块对算法和系统结构进行建模。

本文设计的低通滤波器的频率为3400Hz～3500Hz，采样率为40kHz，通带波纹为0.01dB，阻带纹波为65dB，采用System generator与Matlab Simulink模块的结合进行硬件协仿真，通过采用不同频率的正弦信号来测试该滤波器的性能。

图4 基于内插CIC的FRM低通滤波器的结构模型

本文的积分梳状滤波器采用多级内插式的积分梳状滤波器，为了进行对比本文也对多级抽取式CIC设计的FRM滤波器和基本结构的FRM滤波器进行了研究。为了满足设计要求本文采用5级CIC滤波器作为去镜像滤波器，来进一步降低旁瓣电平，由于CIC内插滤波器可以将采样率提高相应的倍数，所以在与传统等波纹法设计的滤波器进行比较时要加入相应的降采样模块使采样率保持一致，同时为了保证时序的正确，当积分梳状滤波器中的差分延时因子为1时，积分梳状滤波器中有相应的延迟单元，降采样模块中也有延迟单元，所以在积分梳状滤波器后增加值为1的延时单元。对于每个子滤波器的设计都采用FIR滤波器设计中的线性相位结构进行设计，由于系数的对称性，采用折叠结构可使所设计的滤波器的乘法器数量减少一半左右，同时也要区分偶数阶次和奇数阶次滤波器所需要延时单元的不同。整个滤波器的结构如图4所示。

为了与等波纹切比雪夫逼近法产生的滤波器进行比较，本文选取了两个频率不同的正弦信号作为信号源分别通过两个滤波器进行滤波处理，滤波后的频谱如图5所示。下图为采用等波纹法设计的滤波器滤波后，Simulink的输出数据导入到Matlab后编写代码得到的频谱结果。

图5 等波纹法滤波后的频谱图

采用本文方法设计的FRM滤波器滤波后，将Simulink仿真输出导入到Matlab环境中，通过编写相应的Matlab代码得到对应的频谱图如图6所示。

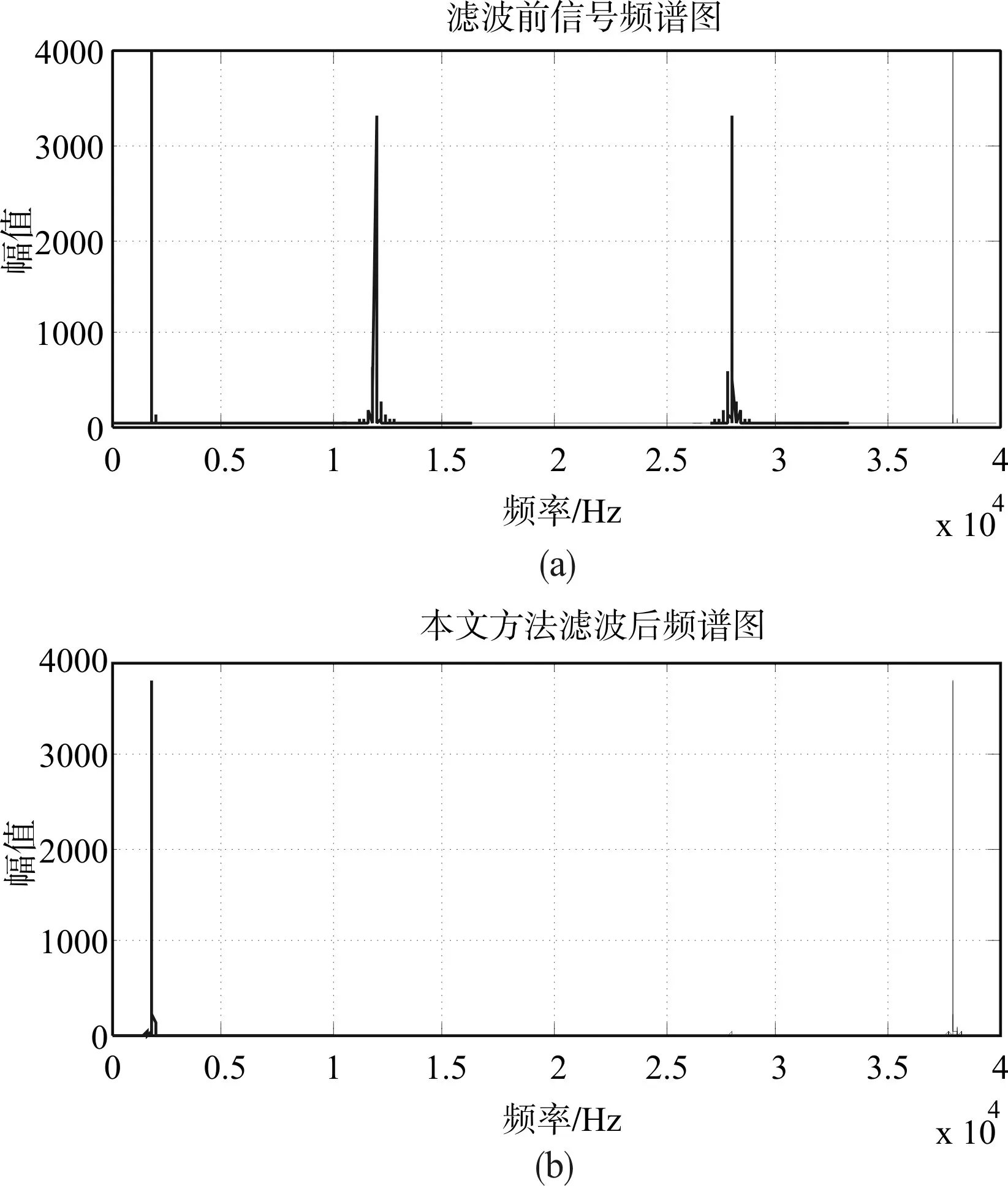
图6 滤波结果Matlab频谱图

将上述结果与采用基本一层结构设计的FRM滤波器进行对比，其基本结构图如图7所示。

也将Simulink仿真输出的结果导入到Matlab环境中，通过编写相应的Matlab代码得到对应的频谱图如图8所示。

根据仿真得到的频谱图可以知道，当所取的数据位数和精度都一样时，本文的设计方法和基本结构的FRM结构的设计方法产生的滤波效果是一样的，但是本文所采用的积分梳状滤波器由于没有乘法器，当不考虑级联用到的乘法运算时，在所搭建的模型中比传统直接设计FRM滤波器少使用了26个乘法器，复杂度降低约15%，加法器也有所减少。当选取其他频率进行测试时两者所得波形基本都是一样的。

图7 基本结构FRM低通滤波器结构模型

图8 滤波结果Matlab频谱图

为了说明本文所采用的内插CIC的有效性，采用多级CIC抽取滤波器设计的FRM滤波器进行对比，即将CIC内插滤波器换成CIC抽取滤波器模块，采用与之前相同的信号源，其结构如图9所示。

采用和之前一样的信号源，加入相应的升采样模块使采样率保持不变，运行仿真，采用和之前相同的处理方式，导入到Matlab环境中，通过编写相应的Matlab代码得到对应的频谱图如图10所示。

由图可知所得结果明显不如基于多级CIC内插滤波器设计的FRM低通滤波器，所以不适合用在FRM滤波器的设计中，说明了本文设计方法的准确性。

图9 基于抽取CIC的FRM低通滤波器的结构模型

图10 滤波结果Matlab频谱图

5 结语

本文通过将CIC滤波器应用到FRM滤波器的结构中去在满足设计要求的同时，降低了设计滤波器的乘法器的数量，进而节约了一定的硬件资源，经过分析本文所采用的的方法设计复杂度比传统的FRM滤波器降低了约15%。通过采用System generator进行测试验证，证明了该方法可以在FPGA芯片上实现，使用System generator进行验证，证明了此方法的有效性，提高了设计的效率，缩短了设计周期。