基于DSP的双线性插值算法在图像旋转中的应用∗

（成都理工大学信息与通信工程系 成都 610059）

1 引言

数字图像处理，顾名思义，是完全用数字化的方式来记录图像信息的。又称为计算机图像处理，就是指用计算机及其他相关的数字技术，对数字图像施加某种或某些运算和处理，从而达到某种预期的处理目的。例如图像的数字变换中的几何变换——图像旋转，它利用插值算法对输入图像进行加工得到输出图像［1～2］。若是采用传统的缩放算法处理图像，图像放大后有很严重的马赛克，缩小后有很严重的失真，图像效果不好，但是采用双线性插值算法却能较真实地反映图像信息［3］。

此外，双线性插值算法在其他领域也有着较好的应用，例如：程相正指出插值技术能够保持图像原始信息的同时显著提高图像分辨率，增加图像清晰度的优点，并将双线性插值算法应用于提高低分辨率传感器所成图像的分辨率［4］。王伟强通过分片线性插值与双线性插值对比得出，双线性插值算法满足解算精度和时间精度要求，更适用于装定器的弹道解算［5］。张红梅将双线性插值算法应用于姿态画面俯仰刻度线数值、倾斜角指示三角的绘制，证明该算法适用于任何图像的旋转、平移变换，计算量适中且得到的图像质量高［6］。Timofeeva，N.E.提出了一种改进的双线性插值算法，利用方向场理论对数字图像进行校正与图像增强［7］。Bruns，Angelika将双线性插值算法与有理Krylov算法相结合，构成双线性模型降价方法，用于保持参数系统的稳定性。Li W为了解决使用了一个简单的双线性插值作为观察所造成的多重网格三维变分（3DVAR）格式成本函数中的映射算子，而采用了数据同化方案［8］等。诸如此类的应用和研究还有很多，这足以说明双线性插值算法的应用越来越广泛，本文将着重介绍双线性插值算法在图像旋转中的应用。

2 系统设计

2.1 图像旋转

图像旋转的原理就是让目标图像按照指定角度旋转相应的度数，但是坐标点离中心的位置却不会改变，只是图像在位置上发生变化。设计中的旋转变换包括旋转公式和双线性插值公式，双线性插值算法的原理是将待求像素点的灰度值取为与它相邻的四个点的灰度值在行和列两个方向上的线性内插［9］。现以平面坐标的旋转变换为例，简述图像旋转原理如下：在下图坐标系下，设y轴向上为正方向，x轴向右为正方向，图像的宽和高分别x size、y size，从坐标系内任选一点（x0，y0），该点经过旋转后产生新的坐标（x1，y1）。并且点（x0，y0）与原点相距r，先将该点与原点相连，再与x轴相连，测得夹角为α，令旋转角度为θ［10］，旋转示意图如图1。

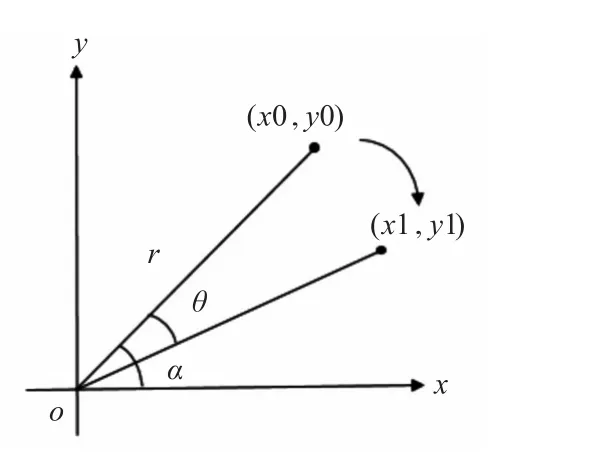
图1 图像旋转

旋转前：

旋转后：

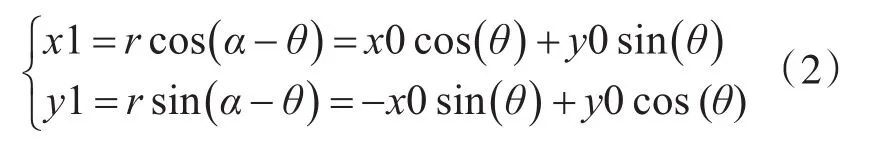
双线性插值算法的示意图如图2，以图像中心为坐标原点，假设在经过旋转后图像的坐标为P（x，y）。图中各点的坐标分别为：Q11（x1，y1）、Q12（x1，y2）、Q21（x2，y1）、Q22（x2，y2），p=x-［x］，q=y-［y］，x1=［x］、y1=［y］，其中［m］表示不超过m的最大整数。

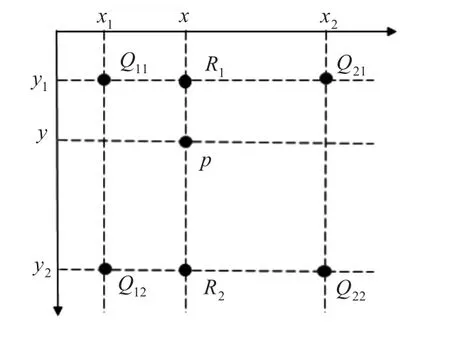
图2 双线性插值算法

先做一次X方向上的插值，由点Q11（x1，y1）和Q21（x2，y1）的灰度值得到点R1（x，y1）的灰度值为

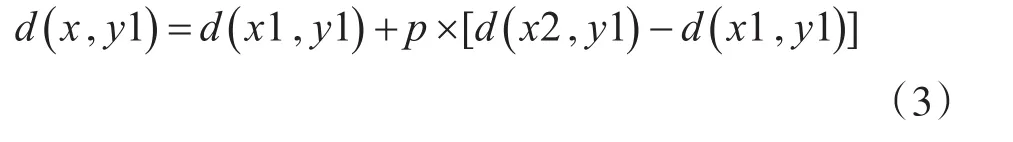
再做一次X方向上的插值，由点Q12（x1，y2）和Q22（x2，y2）的灰度值得到点R2（x，y2）的灰度值为

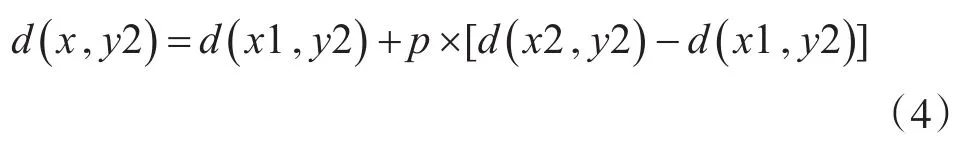
由R1和R2的灰度值在Y方向上做一次插值，得到P点的灰度值为：

此时 d（x，y）、d（x1，y1）、d（x1，y2）、d（x2，y1）、d（x2，y2）分别代表点P、Q11、Q12、Q21、Q22的灰度值。

若是要考虑图像的动态旋转，则需要建立在图像单次旋转的前提下，在程序中通过对图像输入输出的赋值、循环运算。在图像旋转基础上加入的图像动态旋转，实现特定场合的实时图像采集和旋转一体化设计，极大地提高了系统的实时性，增强了系统的可扩展性［11］。

2.2 图像缩放旋转

图像的缩放原理与旋转原理类似，通过原始图像和比例因子得到新图像的大小，并创建新图像［12］。图像缩放功能是一种最基本的功能，数字图像的缩放方法以及图像经过缩放以后的质量，对于整个系统的性能和质量都是至关重要的［13］。图像放大虽然让局部图像更容易观察，但是却会使图像变得不清晰。图像缩小则会增强图像的清晰度。完整的算法可描述为假设fx为横向缩放因子，fy为纵向缩放因子，要把原图的点映射到新图中去的变换如下，其中两点的坐标分别为（x0，y0）、（x1，y1），坐标之间的对应关系为

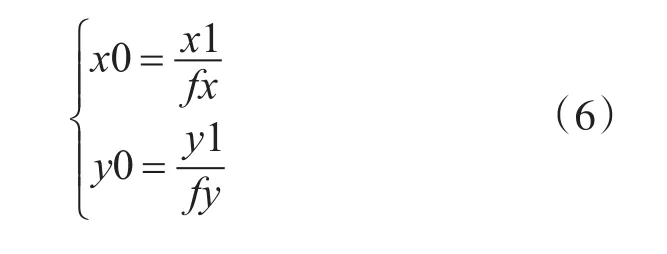
3 实验结果与分析

3.1 实验结果

1）图像旋转

以灰度图为处理图像，进行一定度数的连续旋转，并截取其中的从15°～45°的部分图像，结果如下：

图3 旋转结果图

2）图像的缩放旋转

同样以灰度图像为处理图像，经过多次试验后发现，当缩放因子为0.7时，图像才能尽可能不旋转出矩形框范围。图4的旋转度数分别为：45°、90°和135°。

3.2 结果分析

图3（b）、4（b）作为单次旋转结果，图3（c）和图4（c）、（d）作为动态旋转结果。从结果图来看，图像旋转会丢失像素点，并使图像失真。这是因为图像旋转几乎都靠公式实现，根据设定的旋转角度不同，难免会造成图像直接不完整显现、丢失像素点、出现黑灰斑点。并且会造成像素点的溢出，有些图像边缘还会呈现锯齿状，这是因为测试程序所用的图像不是方图，而是大小为142mm*140mm的矩形图，所以像素点在旋转过程中就会发生移位，系统的偏移量会让数据溢出。这种溢出主要分布在图像矩形框的边缘，测试中同样是旋转45°，单次旋转溢出的像素点加起来约占原始图像的1.5%左右；动态旋转由于存在旋转周期，所以像素点溢出情况略为严重，约为1.6%；缩放旋转在缩放因子为0.7时，就能基本保证像素点不丢失，并把数据溢出很好地控制在1.4%。通过比较分析可知，要想解决图像像素点的丢失和数据的溢出问题就要把图像缩小一定的比例后旋转，这样就可以减少相对的损失，并且结果相对于直接旋转来说是较好的。

图4 缩放旋转结果图

4 系统性能分析

双线性插值算法处理后的图像质量较高，不会出现像素值不连续的情况。但是计算灰度值的过程存在着大量的浮点运算，加上图像的像素点很多，所以是一个较为耗时的过程。经过测试，程序完成一次45°的旋转所用时长很长，因此有必要分析一下程序的优化策略，每次优化后保持与原来完全相同的步骤不变，观察运行时长。优化方法如下。

1）将原图与结果图的几何中心对齐。由于两幅图的原点均选择图像左上角，但是图像最下边的像素点实际没有参与计算，所以得到的结果图相对于原图而言是偏左上的。解决这个问题最好的办法就是将两幅图像的几何中心重合，时长能提升约10s。

2）将有关正余弦函数的计算提取到循环外。未经此步骤前，函数每次循环都要去计算旋转前像素点的坐标，并且是重复的，显得既多余又浪费时间，所以把像素点的坐标值提前计算好之后赋给一个浮点数，循环时直接去调用会节省大约5s的时长。

3）将浮点运算转换为整数运算。双线性插值公式中存在的浮点运算是耗时的主要原因，若是能将浮点数取整，则会节约很多时间。即需要先将浮点数乘以一定的放大倍数，再除以与其相对于的整数。综合放大倍数不能过大、过小，并且要考虑速度，选择2048这个数最为合适。至于除以对应的整数，由于移位运算的运行速度快于除法运算，故在编译时，将程序改写为右移22位。改进后，速度较之前有很大的提升。

5 结语

双线性插值算法实现的图像旋转有着算法简单、运算速度快的特点，并且能在一定程度上保证图像的质量。但是算法具有低通滤波器的性质，使高频分量受损，所以可能会使图像轮廓在一定程度上变得模糊。特别是图像在连续多次旋转之后，边缘变得更模糊。同时，考虑到图像的直接旋转可能会影响图像的质量，在实际中通常加入缩放因子，但是单次缩放之后图像失真严重，难以达到理想的效果。此外，本文的不足之处是：在算法上任然没有很好地解决图像多次旋转后失真严重的问题，这将对结果图像造成一定的影响。