对大学物理课程中“e指数规律”的探讨

2020-06-10陈学文张家伟刘春兰

物理与工程 2020年2期

陈学文江秦张家伟刘春兰

(重庆科技学院数理与大数据学院，重庆 401331)

大学物理课程主要分为力学、热学、电磁学、光学和近代物理五部分，从其物理运动机理来看，彼此之间似乎是互不关联的。然而大学物理课程又是一门规律性很强的学科，许多看来似乎互不相干的物理现象，在某种意义上也遵循着共同的规律。例如：万有引力和静电场力均满足“平方反比”定律，二者都是保守力，做功与路径无关，均可引入相应的势能，因此可以将二者“统一”起来描述[1,2]；质点的平动与刚体的定轴转动，它们的物理规律具有高度相似性，在学习刚体定轴转动时，结合质点平动相关知识点，只要对应相应的物理量和物理规律，可快速掌握刚体定轴转动相关知识[3]；静电场和恒定磁场同样有很多相同的规律，用高斯定理和环路定理描述二者场的性质，在求解静电场和恒定磁场时，分析计算过程也具有相同的规律[4]。

常数e与物理学有密切联系，物质运动中常常有e的身影。在数学上，某一变量的改变率与它本身成正比时，此改变量的数学形式为e-指数函数的形式。文献[5]讨论了自然常数e与物理学的关系。在许多物理过程中，相应的物理量满足“e指数规律”。例如：力学中质点运动过程中受到与其速度成正比的粘滞阻力的运动，刚体在定轴转动过程中受到阻力矩的转动，热学中的等温压强公式，电磁学中的暂态过程，介质对光的吸收和散射，原子核的放射性衰变等，均满足指数规律。此外，在复利计算、老鼠(细菌等)增长与时间的关系、化学污染的衰退时间、化学反应中浓度与反应时间的关系等问题，也满足e指数规律。文献[6]讨论了常数1/e在电磁学中的重要性及其物理意义。在本文中，笔者对大学物理课程中满足指数规律的物理问题做了讨论和总结。希望通过这些实例，展示不同物理现象之间相关联的规律性，显示数学规律在物理研究中的作用。

1 大学物理课程中的指数规律

1.1 力学中的指数规律

质点或物体在粘滞流体(如空气、水等)中运动时，当速度不太大时，其所受到的粘滞阻力与速度的一次方成正比。设有质量为m的质点在粘滞液体中运动，初速度为v0，质点在运动过程中受到粘滞阻力Fr=-kv且受到的其他合外力为零(如高台跳水，运动员入水后所受到的重力与浮力相等)。根据牛顿运动定律可得

(1)

对上述一阶微分方程分离变量并积分：

(2)

另外一种情况是质点在运动过程中所受到的合外力满足F=a-bv(例如小钢球在蓖麻油中下落，在下落过程中受到重力、浮力和粘滞阻力Fr=-bv的作用)。在此情况下有

(3)

(4)

类似于质点的阻尼运动，在刚体定轴阻尼转动中也存在着指数规律。例如，齿轮或风扇等的定轴转动。若关闭齿轮和风扇的电源，它们将在轴的摩擦阻力矩Mz=-kω作用下运动。其角速度ω与t的关系满足ω(t)=ω0e-kt/J时，受到恒定力矩M和阻力矩的共同作用，其角速度ω与t满足ω(t)=ω0(1-e-kt/J)。

1.2 热学中的指数规律

玻尔兹曼把麦克斯韦速率分布推广到气体分子在任意场中运动的情形，从而得到了重力场中的等温压强公式，并证明等温压强公式(对流层中大气压强与高度的关系)满足e指数规律。一般条件下，大气压强和温度均会随着高度的变化而变化，且变化十分复杂，因而对大气压强随高度变化的研究也十分困难。为了加强对大气压强变化规律的探索，本文先研究在等温大气中压强的变化规律。关于地球表面压强问题，文献[7]分别从分子运动论的观点和力学的观点对此作了详细探讨。正如文献[7]中所指出的地球本身是一个球体，因而讨论大气压强时所选取的气体体积元应为如图1中所示的锥形(阴影部分)。此外，除大气重量外其他因素也有影响。由于地球半径很大，因此，在理想情况下可将大地看做平面，因而图1中的锥形空气柱可看成圆柱形空气柱如图2所示。首先假设等温大气处于平衡态，现在选取垂直高度为z～z+dz，面积为S的一薄层气体为研究对象，分析这一等温大气薄层气体的受力情况，如图2所示。

图1 地球表面气体压强示意图

图2 等温压强示意图

其中，p为气体薄层底部受到的压强，dp为气体薄层上下表面的压强差，ρ(z)为高度为z处的大气密度，g为重力加速度且不随高度变化。由于该大气系统处于平衡状态，应该达到力学平衡，分析其受力情况为pS=(p+dp)S+ρ(z)gSdz，即

dp=-ρ(z)gdz

(5)

(6)

(7)

上式称为等温压强公式。其中p0是海平面的大气压强，Mm=0.029kg/mol为空气摩尔质量。

在实际情况中，气温也与海拔有关，在对流层，海拔每升高1000米，气温下降约0.6摄氏度，温度与海拔的关系可表示成T=T0-αz，α=0.006K/m。在此情况下，(6)式变成

(8)

(9)

完成积分运算可得

(10)

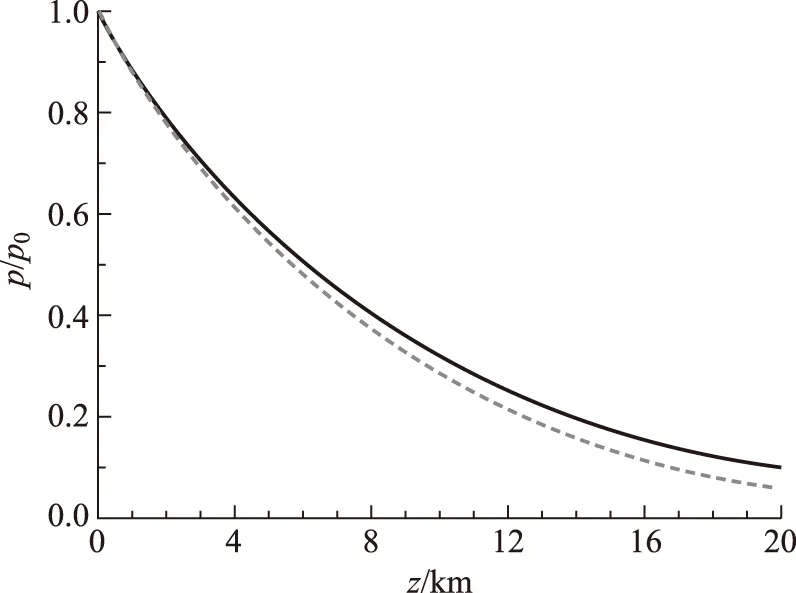
图3 大气压强随海拔高度的变化

图3给出了理想情况下的等温压强和考虑高阶修正的压强随海拔高度的变化。图中实线表示等温压强随海拔高度的变化，虚线表示考虑了温度影响的压强随海拔高度的变化。

1.3 电磁学中的指数规律

直流电路中的暂态过程:暂态过程一般经历时间很短,但出现的现象有时非常重要。如发电、供电设备由于开关操作所引起暂态过程中,某些部分可能出现比稳态时大数十倍的电压、电流,严重威胁电气设备和人身安全，但在电子电路中却有巧妙应用。

(11)

分离变量并积分，得

(12)

图4 RL电路的接通

若t=L/R时，i(t)=I0(1-e-1)=0.63I0，当电流从0增加到恒定值的63%所需的时间为L/R。

(2) 已通电RL电路的短接(图5)。当通过RL的电流已经稳定以后，按下开关K，源电路被开关K所在的短路线cd分为两个互不影响的回路：abcda和dcfgd。对于含R、L的回路abcda，K接通后虽然它已经脱离电源，但由于L的自感作用，该回路的电流还要持续一段时间才会消失。

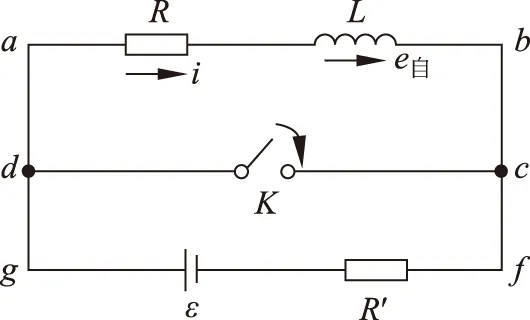
图5 已通RL电路的短接

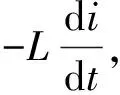
(13)

若t=L/R时，i(t)=I0e-1=0.37I0，当电流从I0递减到恒定值的37%所需的时间为L/R。

L越大，R越小，时间越长，电流增加或递减得越慢。L/R标志LR电路中暂态过程持续时间长短的特征量即时间常量，用τ表示，时间常量τ越大，暂态过程中电流变化越慢。

1.4 光学中的指数规律

光在穿过介质时，介质会吸收部分光。此过程可用朗伯-比尔定律表述：光被透明介质吸收的比例与入射光的强度无关；在光程上每等厚层介质吸收相同比例值的光。如图6所示，一束光穿过介质，介质对光的吸收系数为α，即Iout-Iin=-Iinαdx。可用微分方程将其表示成

(14)

分离变量并积分，可得

I(x)=I0e-αx

(15)

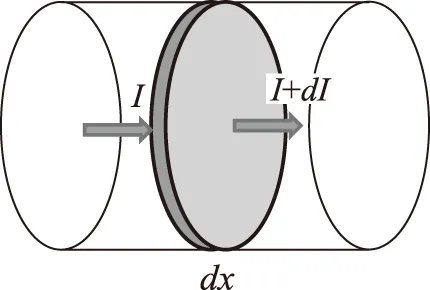
图6 光穿过介质时吸收的示意图

1.5 放射性元素衰变的e指数规律

将一定量的某放射性元素单独收存起来，它的数量会逐渐减少，因为一部分经放射过程变成另一种元素了。这叫衰变。在足够多的原子核中，每一个核在什么时候发生衰变是不能预知的。但是如果在短时间dt内，有dN个核改变，从统计观点，改变率dN/dt必定与当时存在的总原子核数目y′=-ky成正比，即

(16)

λ是比例常数，是放射性物质衰变快慢的标志，成为衰变常数。令t=0时e-1≈0.367，上述方程的解为

N(t)=N0e-λt

(17)

2 指数规律总结

综合以上具体例子，表1简要总结出了大学物理课程中遵循指数规律的部分物理过程。

表1 满足指数规律的部分物理过程

自然界中遵循指数规律的物理过程是广泛存在的，这些物理过程离不开形如y′=-ky和y′=c-ky类型的一阶微分方程，其通解分别为y=y0e-t/τ和y=y0(1-e-t/τ)因此这类微分方程在物理上的重要性是不言而喻的。由于指数规律衰减很快，所以y很快趋于0或y0。例如球形小球在流体中下落(如“落球法测量蓖麻油的粘滞系数”实验中小钢球在蓖麻油中下落，“密立根油滴”实验中油滴在空气中下落)时，在雷诺数不太大时其受到的粘滞阻力可由斯托克斯公式Fr=-6πηrv给出。此情况下6πηr/m相当于式(4)中的b，“弛豫时间”为τ=m/6πηr=2r2ρ/9η，可以看出小球半径越小、流体粘滞系数越大，“弛豫时间”越短。对于蓖麻油，其粘滞系数与温度有关，温度为20℃时η20℃=0.95Pa·s，钢球半径取r=1mm，钢球密度ρ钢=7900kg/m3，在此情况下弛豫时间τ=0.00185s。由于e-7≈0.0001，1-e-7≈0.999，钢球经过7τ=0.013s的时间便达到最终速度的0.999倍，此时可以认为钢球已经达到匀速；对密立根油滴实验，空气粘滞系数η=1.83×10-5Pa·s，油滴典型半径r=8.0×10-7m，油滴(钟表油)密度ρ油=981kg/m3，则τ=3.43×10-5s。油滴经过7τ=2.4×10-4s的时间便达到匀速。在RL电路中，电阻越小、电感越大，弛豫时间τ=R/L越大。又如对于一般家用40W日光灯镇流器的电感约为1H，20W日光灯镇流器的电感约为1.2H，8W日光灯镇流器的电感约为2H，它们的弛豫时间约为0.0003～0.001s之间，则RL电路中电流经过很短时间(≤0.007s)便衰减到0或者增加到I0。可以看出，由于e指数衰减很快，实际中物理量会迅速达到常量或衰减到零。