从数学本质谈“两角差的余弦公式”教学难点的突破

吴建洪

摘    要：在“两角差的余弦公式”教学中，教师可以运用“几何综合法”，从通性通法和数学本质的角度，推导公式，发展学生的数学核心素养.

关键词：两角差的余弦公式;几何综合法;通性通法;数形结合;核心素养

浙江省现行人教A版普高数学必修4教材中“两角差的余弦公式”一节，是高中数学教学中非常重要的概念课.在本节课教材处理中，有几处让教师普遍感到为难的地方，其中最难的无疑是对教材中运用单位圆中的三角函数线，结合几何方法，探索特殊情况下两角差余弦公式的结构.

教材运用“几何综合法”处理如下：

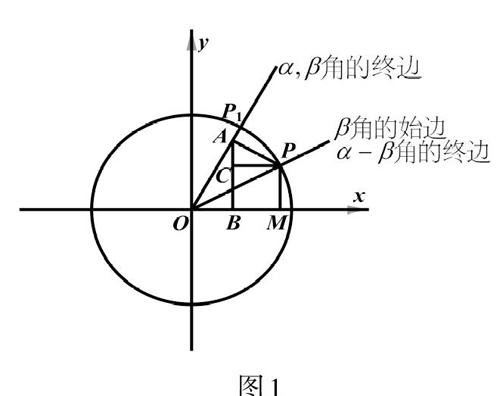
设[α，β]都是锐角，且[α>β]，如图1，令[α=∠xOP1]，[β=∠POP1]，则[∠xOP=α-β]，过点[P]作[PM]垂直于[x]轴，垂足为[M]，则[OM=cos（α-β）].

又过点[P]作[PA]垂直于[OP1]，垂足为[A]，过点[A]作[AB]垂直于[x]轴，垂足为[B]，过点[P]作[PC]垂直于[AB]，垂足为[C]，那么[cosβ=OA，sinβ=AP]，并且[∠PAC=∠xOP1=α]，于是[cos（α-β）=OM=OB+BM][=OB+CP][=OAcosα+APsinα][=cosβcosα+sinβsinα].

近期，听了多位教师关于这一课的公开课，许多教师在教学中基本照搬上述教材中的探究过程，但最后都无奈地照搬教材中的原话，坦承：“上述结果是否在两角为任意角时也成立，要做不少推广工作，并且这项推广工作的过程比较繁难.”随后要求“有兴趣的学生可以在课后自己动手试一试”这样的处理，让原本对用“几何综合法”推导公式充满期待的学生大失所望.

困惑产生疑问.教科书采用“几何综合法”，以“夹叙夹议”的方式详细展示探索过程，难道仅仅是为了能让学生直观感知特殊情况下的公式结构？对此，笔者就如何突破这一教学难点，从学科知识本质和通性通法的角度，谈谈看法.

一、对教材“几何综合法”的本质解读

为使推导过程直观简洁，教材在几何构图过程中作了以下两个方面的精心设计.

一是将角[α-β]的始边与[x]轴的正半轴重合，使角[α-β]的正弦线[MP]、余弦线[OM]均与坐标轴垂直，便于学生直观观察和表示，也便于学生在之后的推导中向已知角[α，β]的正弦线、余弦线直观转化.

二是巧妙构造含有[α，β]角的直角三角形，在直角[△OAP]中直观体现[β]角的正弦线、余弦线的同时，使直角[△OAB]、[△ACP]中的直角边能用角[α]的正弦、余弦值间接表示.在此基础上，推导得出[cos（α-β）=cosαcosβ+sinαsinβ].

倘若在接下来的教学中，教师引导学生顺势探究得出两角差的正弦公式，必然激发学生浓厚的学习兴趣，并初步感受“几何综合法”作为通性通法在推导公式中的重要作用.

由图1，容易得

[sin（α-β）=MP=BA-CA=sinα?OA-cosα?AP][=sinαcosβ-cosαsinβ].

二、“几何综合法”能推导[α+β]的正弦、余弦公式吗？

显然，学生产生上述想法是非常自然的.在学生学习数学的过程中，与分析、解决问题的能力相比，学生在发现、提出问题等方面的能力相对薄弱.对于本节课，教师若能紧紧抓住教材中的素材，启发引导学生提出有价值的问题，必能成为本节课的一大亮点.

由之前构图的经验，组织学生探究如下：

设[α， β， α+β]都是锐角，如图2，令[∠xOP1=α， ∠P1OP=β]，则[∠xOP=α+β].

由于[PA⊥OP1， AC⊥PM]，得

[∠PAC=90?-α]

所以

[cos（α+β）=OM=OB-MB=OB-CA]                             [    =cosα?OA-cos（90°-α）?PA]

[=cosαcosβ-sinαsinβ]

同理可得

[sin（α+β）=MP=MC+CP=BA+CP=sinα?OA+sin（90?-α）?PA]

[                     =sinαcosβ+cosαsinβ]

数学教学历来注重数学本质和通性通法，淡化单一化的解题技巧.如果让学生真实经历上述探究过程，我们一定能从学生的神情中感受到他们内心的欣喜，也一定能使学生深切感受到通性通法在问题解决中的重要性.

我们一直致力于课堂教学改革，积极倡导启发式、探究式等教学方式，以突现学生在教学中的主体地位.对于教材中没有讲到或讲透的，且又能较好反映学科知识与思想方法本质的教学内容，教师一定要充分利用好这些难得的素材，适度挖掘，巧妙设计，精心组织学生开展真正意义上的探究活动，实现有思维深度的学习.

三、对教材“几何综合法”能作进一步改进吗？

在实际教学过程中可以發现，学生对于教材中[β]角的构建感觉不够自然.基于认知基础，学生更习惯于让角[α，β]的始边都与[x]轴的正半轴重合.那么，这样相对自然的处理，能否导出公式呢？

设[α，β]都是锐角，且[α>β]. 如图3，令[∠xOA=α，∠xOB=β]，则[∠BOA=α-β]， 且[∠BCF=∠xOA=α]，

于是

[cos（α-β）=OC=ODcosα=OE-DEcosα=cosβ-FBcosα=cosβ-sinα?BCcosα=][cosβ-sinβ?sin（α-β）cosα]

得

[cosβ=cosαcos（α-β）+sinαsin（α-β）]

同理可得

[sinβ=sinαcos（α-β）-cosαsin（α-β）]

显然，这一结果与之前的公式本质上是完全一致的.对于公式推导，我们努力使过程简明易懂，力求形式最简，所以充分说明了教材处理方法的合理性.

当然，由于受课堂教学时间的限制，上述所有的探究过程不可能在课堂上完整呈现，教师应该告诉学生，教材中的“几何综合法”是一种通性通法，相关推导可以作为探究性作业让学生课外完成，通过自主探究，可以加深学生对公式和通性通法的理解.

由于“几何综合法”对数学问题中的几何元素有比较直观、明确的要求，难以处理相关量的任意情形，所以不能较好地推导出任意两角差的余弦公式.从教材编排意图看，一定程度上也突现“向量法”的优越性（当然用两点间距离公式推导也很方便）.即便如此，我们也不能贬低“几何综合法”这一蕴含人类巨大智慧的数学方法以及运用这一方法在解决问题中的重要作用.

四、从数学本质看“几何综合法”

（一）体现几何与代数的紧密联系

几何与代数是高中数学课程的主要内容之一，在教学过程中，我们应突出几何直观与代数运算之间的融合，即通过形与数的结合，感悟数学知识之间的关联，加强对数学整体性的把握与理解.由于在三角函数的研究过程中有许多几何元素，如单位圆、三角函数线等，看似代数形式的两角差的余弦公式，对它的推导，无论是用向量法中的数量积公式，还是用坐标法中的两点间距离公式，其本质都是充分运用数形结合思想来解决问题的.在数学研究中，从数形结合的角度研究中学数学是一种十分重要的数学思想方法.当我们在遇到数量关系时，常常尝试着用几何图形把它表示出来.

（二）“几何综合法”是解决几何问题的重要方法之一

中学数学研究几何问题一般有三种方法：几何综合法、坐标法和向量法.几何综合法依据基本的逻辑原理，不使用其他工具，从公理或基本事实出发，通过演绎推理，对几何元素及其关系直接进行讨论，给出几何论证.坐标法或向量法，是以数和数的运算或向量和向量的运算为工具，对几何问题进行分析讨论.其中，几何综合法对培养学生的数学抽象、逻辑推理、直观想象、数学运算等数学学科核心素养有着十分独特的重要作用，教材中用这一方法探究两角差的余弦公式的结构特征，是培养、形成数学学科核心素养的极好素材.

（三）一以贯之体现单位圆在三角函数研究中的重要作用

单位圆是我们定义三角函数、推导同角三角函数基本关系式和诱导公式、理解三角函数的性质、作三角函数图象等内容的直观载体和重要工具.在两角差的余弦公式推导过程中，无论是几何综合法，还是向量法或坐标法，都用到单位圆这一重要数学模型，体现不同数学方法之间的内在联系.

教材是实现数学课程目标、发展学生数学学科核心素养的关键性教学资源，教材提供的学习素材和具体內容是开展“教”与“学”活动的基本依据.在教学过程中，要善于把握教材的编写意图，更有效地利用蕴含在数学知识产生、发展过程中的重要数学思想和数学方法，使我们的数学活动更加绚烂多彩，富有创意.