上海黄金期货周日历效应的实证研究

一、前言

日历效应的存在是金融市场上一种十分有趣的现象，国内外许多学者对此进行了研究。而前人在研究此现象时，更多的研究集中在股市上，而对期货市场较少涉及。特别是国内，期货市场发展时间短，相关的研究也更少。华仁海（2004）研究发现大豆的收益率和波动并没有日历效应，这和国外的研究结果相左。李坚强（2009）对中国期货市场上的大豆、强麦、铜、铝和燃油期货进行研究。作者发现这5种期货的收益率都具有明显为正的“周一”效应，而波动率的星期效应较弱。甘欢欢、焦建玲（2010）运用GARCH-M模型和TGARCH研究了原油价格的周日历效应及杠杆效应。作者发现原油期货价格波动存在着杠杆效应，星期五的收益明显为正且具有长期稳定趋势，而波动的变化并不明显。史继文、吴浩然（2018）采用2010-2017年天然橡胶期货的结算价和成交量为样本数据，对天然橡胶期货做ARMAGARCH建模进行实证检验。作者发现，星期二的橡胶期货收益率明显为负，星期一的橡胶期货成交量变化率明显为负。

针对以上情况，本文选取研究较少的中国黄金期货作为研究对象，对其周日历效应进行了实证分析，探索其是否存在及分析具体特征。同时本文针对样本数据的特殊性选择拟合效果最佳的GARCH模型，之后再对模型进行实证检验，最终得出实证结果，以期弥补此项研究领域的不足。

二、数据处理及模型选取

（一）样本选取。本文选取上海黄金期货2015年1月至2019年11月，共记5年的日数据，数据样本为黄金期货的每日收盘价，最终有效的日数据共计1064条。数据来源为国泰安经济金融数据库与CCER经济金融研究数据库。

本人运用主力合约构造法，选取每年交割月份为6月和12月的黄金期货为代表，构造连续的期货价格序列。例如，2015年1月至2015年5月的数据采用交易代码为AU1506的期货合约价格，2015年6月至2015年11月采用交易代码为AU1512的期货合约价格，之后的时间依次类推。

为保证数据的连续性及平稳性，以对数收益率作为研究指标。

其中，Rt为对数收益率；tP为第t期的收盘价；t为时间，单位为日。

（二）数据处理。对黄金期货的对数收益率做JB检验。黄金期货对数收益率的星期数据序列均值为0.030，标准差为0.825。偏度为0.389，大于零，说明数据右偏。峰度为8.017，高于正态分布的峰度值3。JB统计量为1142.836，P值为0。故该序列不服从正态分布。

对黄金期货数据做平稳性检验，在不含趋势项与漂移项的检验结果中ADF的T统计量为-34.224，小于-2.568。说明即使在1%的置信水平下，序列依然满足不含趋势项和漂移项的平稳。在含趋势项与漂移项的检验结果中ADF的T统计量为-34.248，小于-3.972、-3.416、-3.130。说明在1%、5%和10%的置信水平下，序列都满足含有趋势项和漂移项的平稳。综合上述结果表明，该时间数据序列平稳。

对黄金期货的对数收益率做相关性检验，结果显示，序列的自相关和偏自相关系数均小于两倍的估计标准差，P值均大于置信度0.05。故在5%的显著水平上，数据不存在显著的自相关和偏自相关性。

对黄金期货数据做Arch检验，结果显示，序列中的1阶、2阶、4阶、7阶、8阶、9阶的自相关系数都大于两倍的估计标准差。同时P值均接近于0，小于置信度0.05。所以，黄金期货的星期数据存在显著的自相关关系，ARCH效应存在。

（三）模型选取

Egarch模型不仅可以反映投资者的利空和利好，同时还不受参数设定的限制，故而本文采用Egarch模型。接下来，本文将黄金期货数据代入 Garch模型、Tgarch模型、Egarch模型，并分别作比较，以模型比较结果来最终决定采用何种模型。

1.GARCH（1，1）、GARCH（1，2）、GARCH（2，1）。Garch模型常见的几种模型为GARCH（1，1）、GARCH（1，2）、GARCH（2，1），将黄金期货数据分别代入以上三种模型。拟合结果表明，Garch（1，1）的统计值显著，P值通过1%置信水平下的检验。Garch（1，2）的统计值不显著，P值没有通过5%置信水平下的检验。Garch（2，1）的统计值显著，P值在5%置信水平下显著。综合比较Garch（1，2）、Garch（2，1）、Garch（1，1）的z统计量与P值，发现Garch（1，1）的拟合效果最好。故暂时选定Garch（1，1）模型。

2.TGARCH（1，1）、EGARCH（1，1）。对黄金期货的星期数据，在Garch（1，1）模型的基础上，我们先做TGARCH（1，1）模型拟合。之后，再做EGARCH（1，1）模型拟合，并比较两者的效果。拟合结果为，Tgarch（1，1）的统计量分别为4.427、8.143、-5.934、289.288，对应的P值全为零。Egarch（1，1）的统计量分别为-8.378、7.794、5.213、831.074，对应的P值也全为零。统计值比前者更加显著，P值均通过三种置信水平下的检验。综合比较Tgarch（1，1）和Egarch（1，1），我们选择模型Egarch（1，1）。

综上所述，我们最后选定的模型为：

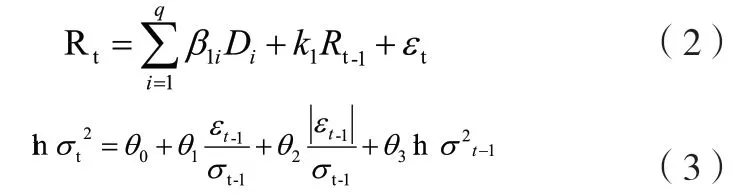
公式2为模型的均值公式，公式3为方差公式。其中，Rt为黄金期货对数收益率，Rt-1为对数收益率滞后一阶。εt为残差项，εt1-为残差滞后一阶。为条件方差，、为条件方差的滞后项。Di为虚拟变量，其值取0或1。在星期效应中，q=5。例如，当交易日为周二时，D2=1，D1、D3、D4、D5=0。其他日期依此规律可以得到。

三、日历效应的实证分析

（一）描述性统计分析。对黄金期货收益率做基本数据的统计，结果显示1064个交易日的黄金期货日收益率均值为0.030，标准差为0.824，表明日均收益率是在零轴附近波动的，但总体上较为稳定。日收益率的偏度为0.389，分布存在正偏离，说明收益率为正日期总体上多于收益率为负的日期。且总体而言，所有数据的峰度均大于三，说明数据序列都不服从正态分布。4.880的最大值和-4.795的最小值，说明上海黄金期货市场上的期货价格仍然存在短期的异常波动。

对黄金期货收益率的星期效应作图分析，可以看出，周一至周五中，只有周二的平均收益率为负数，其余皆为正。且周五和周一的均值明显高于其他日期，显现出收益为正的周日历效应。

（二）模型拟合分析

以公式4为模型做最小二乘回归，对均值做星期效应检验，结果表明，周一至周五的黄金期货收益率的系数均较小，其t统计量也都不显著，P值均大于10%的显著性水平。模型结果说明黄金期货收益率均值的日历效应并不明显。

以公式5做Egarch（1，1）模型检验，对方差做星期效应检验，结果显示，周五的系数为0.070，t统计量为1.705，P值为0.088，可以通过置信水平10%的检验。故此可以得出结论，黄金期货价格的波动存在“周五效应”。而周一至周四的黄金期货收益率的系数均较小，其t统计量也都不显著，P值均大于10%的显著性水平。这说明黄金期货波动周一至周四的日历效应并不明显。

四、结语

本人通过对黄金期货的价格做描述性统计分析和模型拟合分析，对其日历效应进行了实证研究，结果发现其的确存在日历效应。首先，通过描述性统计分析，观察黄金期货收益的星期效应图。我们可以初步推断，上海黄金期货存在显著为正的“周一效应”和“周五效应”。其次，通过适用周数据的拟合模型Egarch（1，1）进行实证检验。模型检验结果表明，上海黄金期货的价格收益的周日历效应不显著，而价格波动存在“周五效应”。综上所述，上海黄金期货的收益率和波动率存在“周五效应”。