基于对抗训练的U-Net神经网络在稀疏投影CT图像增强的应用

黄锦威，萧文鹏，朱思婷，丘皓怡，陈星宇，刘深泉

1.华南理工大学数学学院，广东广州510640；2.华南理工大学计算机科学与工程学院，广东广州510006；3.华南理工大学电力学院，广东广州510641

前言

X 射线CT 技术是一种无损检测技术，广泛应用于医疗检查和工业物品检测等领域［1］。由于X 射线的辐射性，所以在医疗诊断中，对特殊受检者要适当降低X射线剂量或减少探测次数，从而降低检测过程中辐射的影响，但低剂量的X射线投影过程容易受到噪声干扰，而稀疏投影会使探测得到的信息量减少，导致重建的CT 图像带有伪影，影响进一步的医疗诊断。

传统的CT 图像降噪常用滤波函数对图像进行全局滤波平滑，但这种无差别的平滑处理可能丢失CT图像的部分细节信息。而近年来基于神经网络模型的图像处理技术得到广泛研究应用，如图像分类［2］、物体检测［3］、图像超分辨率化［4-6］、图像风格化［7-8］等，在图像数据集测试中取得优于传统方法的效果。Chen 等［9］提出残差编码-解码卷积神经网络（Residual Encoder-Decoder Convolutional Neural Network,RED-CNN）模型用于低剂量CT 图像增强，本研究基于RED-CNN 模型，提出一种基于对抗训练的U-Net神经网络，用于稀疏投影CT图像增强。

1 CT重建算法

CT 图像的重建算法主要分为两类：一类是基于Radon 变换［10-11］的解析类重建算法，另一类是以解方程为主要思想的代数重建算法［12］。

解析类重建算法又可分为滤波反投影法算法［11,13］和直接傅里叶变换重建算法［14］。其中，滤波反投影算法基于反投影法，在其基础上增加卷积滤波过程，具有重建速度快、空间和密度分辨率高等优点，在实际中得到广泛应用；直接傅里叶变换重建算法由于其频域插值计算复杂度较高，在实际应用中常采用重建质量高的滤波反投影法算法［15］。代数重建法是利用投影数据构建一组线性方程，通过求解线性方程组进行图像重建。但是代数重建法计算量大、重建时间长，因此在一定程度上限制了其应用［16］。

由于滤波反投影算法在实际应用中占有重要地位，本研究将对平行束投影的滤波反投影算法的基本原理以及该算法对稀疏投影的重建图像附带伪影的现象进行介绍。

反投影算法的基本思想是：待重建图像中某个位置的像素值，可以通过计算所有经过这一点的投影值的平均值近似得到［13］。以3×3 大小的图像投影为例，原图像中有9 个像素X1,X2,…,X9，分别从0°、45°、90°和135°这4 个方向进行投影，得到投影值P1,P2,…,P16（图1）。投影值Pi(1 ≤i≤16) 和像素值Xj(1 ≤j≤9 )的关系如方程组（1）所示。

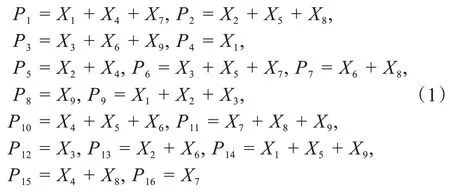
基于方程组（1）得到反投影计算式（2）。

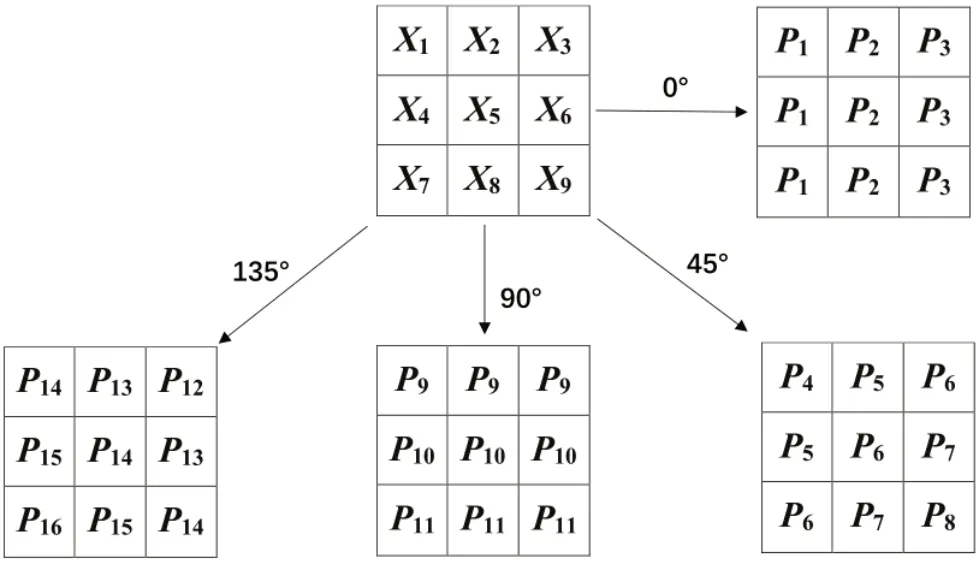
图1 3×3图像在4个不同角度的投影Fig.1 Projection of a 3×3 image at 4 different angles

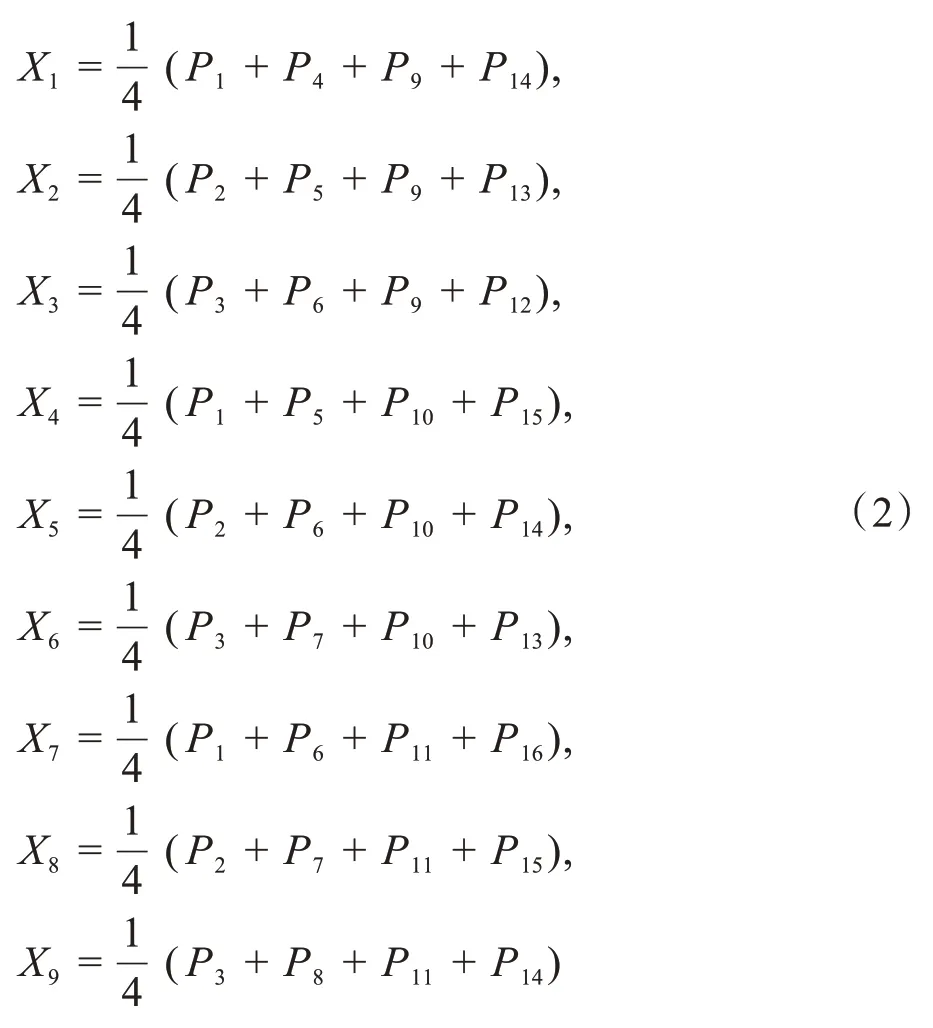
以上示例仅采用4个不同角度进行投影，当图像像素比较多时，为得到高质量的重建图像，需要选取更密集的投影角度，一般是取值跨度180°的多个均匀分布的投影角度。由反投影计算的原理可知，该算法的重建结果是近似的。从图2可以看出由于中心像素的像素值1的影响，使得周围的像素值在重建后变大了。这种在反投影重建中由一个位置的像素值影响其周围位置像素值产生的差异称为星状伪影。产生星状伪影的原因是反投影重建是将一个投影值均匀地反投影到其投影路径的每个像素上，因此当该投影路径上各点的像素值并非均匀分布时，其像素值较大的位置的值会被“分摊”到像素值较小的位置上［17］。星状伪影可以通过增加投影角度或对投影数据进行滤波得到减轻或者去除，由于滤波反投影算法在反投影算法上加入了卷积滤波过程，因而重建效果更好。常用的滤波函数有Hamming、Hanning、R-L、S-L、Cosine等。但在稀疏投影的情况下，即使对投影数据进行了滤波，其反投影结果依然会带有明显伪影和噪点。

图2 3×3图像与反投影计算结果比较Fig.2 Comparison of a 3×3 image and the result of its backprojection calculation

2 基于对抗训练的U-Net神经网络

U-Net 模型由Ronneberger 等［18］首次提出并用于解决医学图像分割的任务，通过低层信息往高层补充，使模型能够处理医学图像的细节。近年来，对抗生成网络GAN［19］被广泛应用于图像的生成与转换，通过内部生成器与鉴别器的对抗、博弈，在对抗过程中生成器不断提高生成更真实目标图像的能力，鉴别器则不断增强自己的鉴别能力，以区分输入图像的真伪。鉴别器直接区分“模糊的、有噪声的CT 图像与清晰、高质量的CT 图像”的能力对于增强模型的性能有引导作用。

2.1 模型与原理

基于对抗训练的U-Net神经网络模型结构如图3所示，模型以稀疏投影数据经过滤波反投影算法重建得到的带噪声和伪影的CT 图像Input（I）作为输入，经过增强模型G（一个浅层的U-Net）处理，输出增强后的CT 图像Output（O）。将输出图像O 与对应的目标图像GT 分别输入鉴别器Decoder（D），鉴别器D对输入进行判断，如果输入是GT，则D倾向于判断为True；如果输入是图像O，则D 倾向于判断为False。鉴别器D 由连续的4 层卷积操作与最后的全连接层FC构成，结构如图4所示。

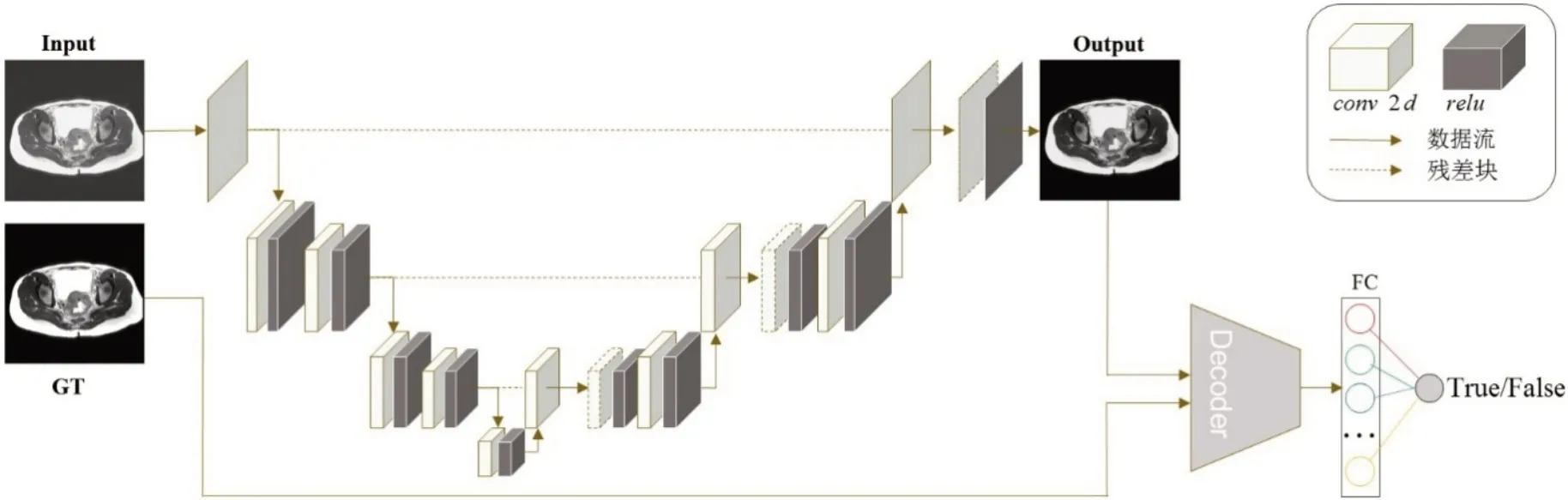
图3 基于对抗训练的U-Net神经网络结构Fig.3 Structure of U-Net neural network based on adversarial training

图4 鉴别器结构模型Fig.4 Structure of the decoder

2.2 目标函数选取

2.2.1 增强网络的目标函数模型采用逐像素的均方差（Mean Square Error）：

其中，H、W分别指图像的高度与宽度。

定义G的对抗损失为：

G的损失函数为：

其中，λ是一个超参数，在本模型实验中取λ=10。

2.2.2 鉴别器的目标函数鉴别器D 的目标函数定义式（6）。

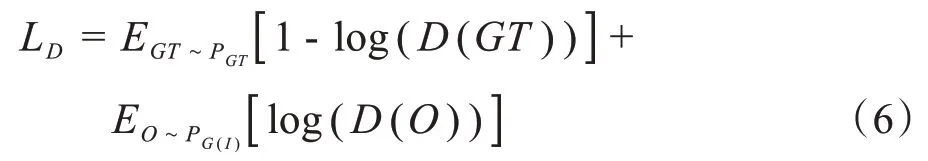
3 实验分析

3.1 数据集选取和处理

模型的训练与测试使用公开数据集TCGACESC 癌症CT 影像中的数据，其中包含2 900 组来自人体不同部位的CT 图片数据。筛选出大小适宜的图片数据1 942组，从中随机选择72组数据作为测试集，其余1 870组数据作为训练集。

将每组CT 图像数据读取为二维矩阵GT∈RH×W。假设CT 扫描在不同角度进行探测时设备参数条件相同，利用Radon变换模拟X 射线投影过程，获取图像在180个角度（相隔1°进行一次投影）的投影数据，经过滤波反投影重建，得到有噪声和伪影的CT 图像矩阵I∈RH×W。将每个GT 与其对应的I称为一组数据。由于整体训练样本偏少，因此将1 870组训练数据进行裁剪，每组裁剪得到不同位置的5组图像数据，将裁剪得到的9 350 组数据作为训练集用于模型的训练。

3.2 评价指标

本文采用3种典型的图像质量评估指标。

（1）峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）指的是峰值信号的能量与噪声的能量的均值之比。

其中，MSE 为均方差，计算式如式（3）；MAX 为图像的灰度级，一般取MAX=255。PSNR 值越大，说明两张图像相似度越高。

（2）结构相似性（Structural Similarity,SSIM）是基于两张图像的亮度、对比度与结构这3个方面衡量两者相似度的方法，SSIM值越高，说明两张图像相似度越高［20］。

（3）均方根误差（Root-Mean-Square Error,RMSE）计算式见式（8），用于衡量两组数据的偏差。RMSE值越小，说明两张图像相似度越高。

3.3 实验细节

模型的训练和测试在一台CPU 核为i7、内存32G、内置1080Ti GPU 的服务器上完成，使用的图像分辨率为384×384。测试阶段，无GPU驱动下单张图像的处理时间为（0.353±0.010）s；1080Ti GPU驱动下单张图像的处理时间为（3.406±0.350）ms。

3.4 实验结果

将模型输入图像I和最终输出图像O 分别与数据集中原始图像GT 进行比较，并计算PSNR、SSIM和RMSE，两张图像相似度越高表明图像质量越高。

3.4.1 基于测试集的单样本分析从测试集中随机选择一个样本，本研究提出的模型得到的结果见图5和图6。

图5 模型输出结果与输入样本的比较Fig.5 Comparison of the input and the output of one sample

由图5可知，模型输出图像的3 项评价指标均优于所选的输入样本图像。从图6可以明显发现模型输出图像相比输入样本图像有更少的伪影和噪声以及更清晰的边缘轮廓，细节上更接近原始图像。

3.4.2 基于测试集的总体分析基于测试集中数据，统计本研究提出的模型对测试图像在3 个指标中的表现，结果见表1。其中，提升数值表示模型处理结果相对于未处理图像在相应指标上提升的数值，PSNR 和SSIM 指标的提升数值为模型处理结果的指标值减去未处理图像的指标值，PMSE 指标的提升数值为未处理图像的指标值减去模型处理结果的指标值。提升百分比为指标提升数值与未处理图像相应指标的比值。

图6 图5中图片的局部放大Fig.6 Partial magnification of Fig.5

本研究提出的模型是基于RED-CNN 上的创新，将本研究提出的模型与RED-CNN 的处理结果进行比较，各项评价指标对比如表2所示。

表1 本文模型在测试集上的提升效果Tab.1 Enhancement effects of the proposed model on the test set

表2 本文模型与RED-CNN在测试集上的处理结果比较Tab.2 Comparison of the results of the proposed network with RED-CNN on the test set

从表1的提升数据可知，在平均意义下，本研究提出的模型的处理结果相比于未处理的图像有较大提升，其中SSIM 和RMSE 的平均提升百分比均超过35%。同时某些测试图像的模型处理结果在评价指标意义下差于未处理图像，在72 组测试集中有2 组数据出现负提升，图7为其中一组出现负提升的样本。经人工对比分析，发现这两幅图像在数据集TCGA-CESC 中的原图有较多噪点，而模型处理后减少了图像的噪点，处理后图像更加平滑（图8），因此在基于原图比对的指标下出现了负提升现象。

从表2的对比数据可知，在3 种评价指标下本研究提出的模型的结果与RED-CNN 比较接近，相较于处理前的图像（Input）有明显的提升。本研究提出的模型与RED-CNN 相比，PSNR 得分的极差分别为16.508 4 与16.938 0，RMSE 得分的极差分别为12.768 6与13.106 5，SSIM 得分的极差分别为0.151 8与0.150 0，在评价指标极差意义下本研究提出的模型更稳定。

为了进一步说明模型对稀疏投影重建图像的提升效果，将本研究提出的模型对180次探测（1°/次）重建图像的处理结果与180 次探测（1°/次）、360 次探测（0.5°/次）、720次探测（0.25°/次）和1 800次探测（0.1°/次）的未经本模型增强的重建图像进行比较。图9中3项评价指标的数值为测试集的评价结果的均值归一化，可以看出本文模型相比180次探测的重建图像在3个指标上均有明显提升，PSNR和RMSE指标与360次探测、720 次探测和1 800 次探测的重建结果接近，SSIM 指标则优于1 800 探测的重建结果。说明本文模型对稀疏探测重建的CT 图像确有提升作用。此外，360 次探测、720 次探测和1 800 次探测的重建结果指标上接近，这是因为当探测密度增加到一定程度时，继续增加探测密度对重建图像的质量提升作用并不显著。

图7 出现负提升现象的一组数据的模型输出结果与输入样本比较Fig.7 Comparison of the input with the output of one sample with negative enhancement

图8 图7中图像的局部放大Fig.8 Partial magnification of Fig.7

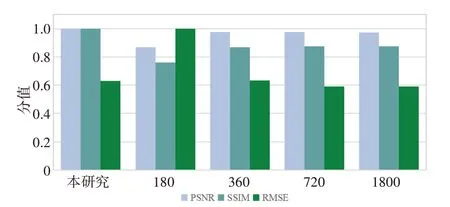
图9 本文模型结果与不同探测密度的重建图像比较Fig.9 Comparison of the results obtained by the proposed network and reconstructed images with different detection densities

4 结论

本研究提出了基于对抗训练的U-Net 神经网络模型，并基于公开数据集TCGA-CESC 癌症CT 影像通过实验计算证明该模型对稀疏投影重建后带伪影的CT 图像有明显的增强效果。在180 次探测测试中，在均值意义下SSIM 指标和RMSE 指标的提升超过35%，且本研究模型对180 次探测重建图像的处理结果在PSNR 和SSIM 指标下优于1 800 次探测的重建图像。说明本研究模型对稀疏探测的条件下的重建图像进行增强，其图像质量接近甚至优于密集探测条件下重建的CT 图像。基于上述研究结果，进一步可以研究模型的稳定性，以及如何通过改良模型框架和调整必要参数使模型有更好的表现。