质子束流蒙特卡罗模型的建立及对脊形滤波器的探究

康月航，盛尹祥子，赵静芳，章青

1.上海市质子重离子医院放射物理科，上海201321；2.上海质子重离子放射治疗工程技术研究中心，上海201321；3.复旦大学附属肿瘤医院放疗科，上海200032；4.上海市质子重离子医院放射肿瘤科，上海201321

前 言

放射治疗是恶性肿瘤综合治疗的主要治疗手段之一，在恶性肿瘤的治疗过程中约60%的患者需接受放射治疗。放射治疗的宗旨是在正常组织保护的前提下给予肿瘤最大的杀伤。目前临床多采用光子治疗，已有的临床研究证实肿瘤的局部控制和剂量密切相关［1-4］，但由于靶区周围危及器官的限制，导致靶区剂量无法提高，从而影响疗效。与传统光子放射治疗相比，质子由于存在特殊的布拉格峰［5-6］，具有精准、低毒的优势，可有效地降低靶区周围正常组织剂量，从而为临床靶区剂量提高提供可能。目前，质子治疗已被运用于临床，并显示了一定的疗效［7-10］。

但目前常采用笔形束扫描技术的质子束流，横向上通过一个个小的笔形束扫描靶区；纵向上，靶区被逐层分割，通过改变束流能量达到剂量与靶区适形［11-13］。由于低能质子束流的布拉格峰很锐利，如48.1 MeV 质子的束流末端最大剂量的80%到束流末端最大剂量的20%的宽度（D80-D20）仅为0.41 mm，临床治疗时需使用多个能量层叠加以保证靶区剂量均匀［14］。考虑到同步加速器一般需要4～6 s 完成一层能量切换，如临床上治疗乳腺癌约使用50层能量，总的能量切换所需时间超过4 min，是临床治疗过程中占用束流时间的主要因素。束流时间的延长也可能导致患者无法耐受，引起体位及器官位置的变化，从而影响剂量分布的精确性。对于前列腺癌，前列腺的位置受膀胱充盈度的影响，如果治疗时间过长，前列腺的位置会改变，靶区位置也会改变；对于胰腺癌，临床上选择主动呼吸控制或门控技术来控制肿瘤的移动，如果质子治疗时间过长，病人可能无法耐受长时间的主动呼吸控制或门控技术，可能导致高剂量质子“打到”靶区周围的危及器官，产生严重的毒性。由于目前质子束流有限，治疗时间的延长同时限制了治疗病人总数。因此，质子治疗迫切需要结合新的手段以缩短治疗时间，提高治疗精确性和治疗效率，增加治疗病人数量。

根据目前文献报道，脊形滤波器可展宽布拉格峰［15-17］。目前文献报道多是研究采用脊形滤波器展宽碳离子布拉格峰，鲜有研究质子布拉格峰展宽的数据［15,18-19］。本研究拟通过建立质子束流蒙特卡罗模拟模型，并模拟脊型滤波器对质子布拉格峰的展宽效果，以探讨通过脊型滤波器展宽质子布拉格峰对临床治疗的应用价值。

1 材料与方法

1.1 蒙特卡罗程序

剂量计算是质子放射治疗中最为核心的部分，蒙特卡罗方法在剂量计算方面有较大优势。蒙特卡罗方法能够模拟粒子输运过程，进行剂量计算，且考虑了真实环境下空气对粒子的散射影响，是目前公认的精确科学的粒子输运计算方法。常用的蒙特卡罗模拟软件有FLUKA、MCNP、MCNPx和Geant4等。相比其他几种软件，工具软件包FLUKA 具有更丰富的粒子种类，同时还有强大的物理学和几何学编辑功能。针对于大多数的应用，FLUKA 使用者不需要编写程序。因此，本研究选用FLUKA 进行蒙特卡罗模拟。

1.2 质子束流测量和模拟及模型验证

依照文献［20］的测量方法获得48.1、59.8、104.5、124.2 和136.2 MeV 的质子束流的水中积分深度剂量分布数据，使用蒙特卡罗程序FLUKA 对上述相同能量的质子束流进行模拟，获得模拟的水中积分深度剂量分布数据。将获得的测量及模拟积分深度剂量分布数据进行归一，利用插值计算束流前端最大剂量50%深度（E50）、束流前端最大剂量70%深度（E70）和束流末端最大剂量80%深度（D80），计算出模拟曲线与测量曲线间E50、E70和D80的差值，反复调整模拟的束流能量及决定束流能量离散程度的能谱分布值，直至模拟和测量之间E50、E70和D80的差值均在0.2 mm 以内。选择并记录最贴近测量积分深度剂量曲线所对应的模拟能量及相应模拟数据。通过对上述5个能量的测量与模拟，找到测量能量与模拟能量的对应关系，建立质子束流的蒙特卡罗模型。利用121.1 MeV 质子束流的测量结果对该模型进行验证。

1.3 A型脊形滤波器

A 型脊形滤波器即三棱柱型脊形滤波器［15,21］，图1为A 型脊形滤波器的平面结构示意图。考虑到多库伦散射的影响，脊形滤波器的材料必须是低原子序数的材料，化学纯度要求高，以确保滤波效果的稳定性。本研究选择有机玻璃薄板（PMMA），密度为1.17 g/cm³。脊形滤波器的总厚度为2.7 mm，包括最小的底盘厚度0.3 mm，底盘是为了保证有机玻璃板的稳定性，每个三棱柱的宽度为1.0 mm。

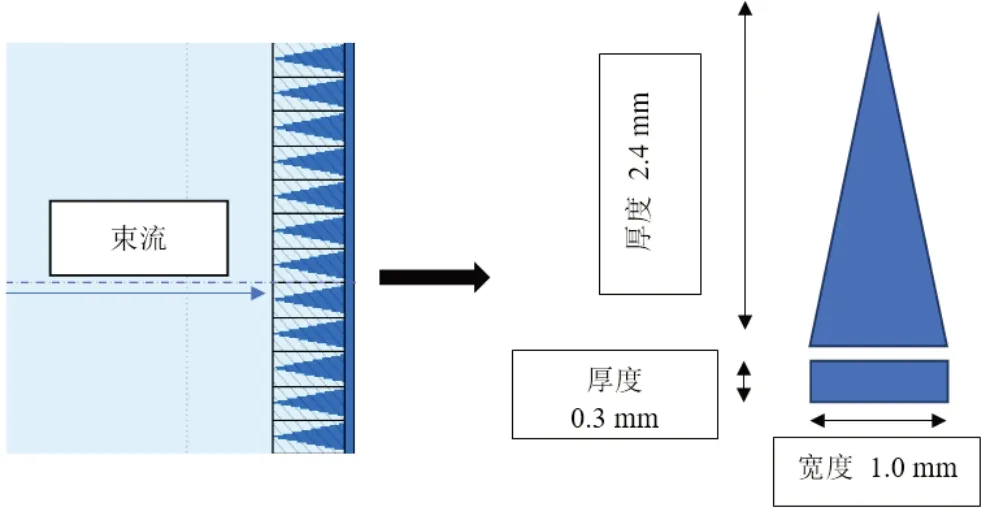
图1 A型脊形滤波器的平面结构Fig.1 Planar structure of A-type ripple filter

1.4 B型脊形滤波器

B 型脊形滤波器即金字塔型脊形滤波器［22］，图2为B 型脊形滤波器平面结构示意图。B 型脊形滤波器材料同样为有机玻璃薄板（PMMA），密度为1.17 g/cm³。横截面为9个宽度递增的矩形组成的金字塔形，每层层厚0.3 mm，矩形宽度依次为0.80、0.70、0.60、0.50、0.40、0.30、0.20、0.10、0.05 mm，共有100个独立的金字塔形结构。

图2 B型脊形滤波器的平面结构Fig.2 Planar structure of B-type ripple filter

1.5 模拟方法

使用FLUKA分别建立A型脊形滤波器和B型脊形滤波器的几何结构。联合使用FLUKA 中的LATTICE卡和ROT-DEFI卡来编辑重复的几何结构，从而构建脊形滤波器的几何模型，并使用USRBIN卡来对剂量沉积进行计算。模拟上述5 档质子束流分别通过A 型脊形滤波器和B 型脊形滤波器的积分深度剂量数据。

1.6 展宽效果分析方法

将上述模拟的水中积分深度剂量数据进行归一。利用插值计算E50、E70和D80，计算束流前端最大剂量50%深度到束流末端最大剂量50%深度的宽度（E50-D50）、束流前端最大剂量80%深度到束流末端最大剂量80%深度的宽度（E80-D80）以及束流末端最大剂量80%深度到束流末端最大剂量20%深度的宽度（D80-D20）。

2 结果

2.1 质子束流蒙特卡罗模型的建立及验证结果

在不使用脊形滤波器的情况下，绘制5个能量质子模拟值与测量值的对比曲线，如图3所示。黑色实线表示模拟值，空心圈表示测量值，从左至右依次代表48.1、59.8、104.5、124.2、136.2 MeV这5个能量的模拟值与测量值曲线。上述5个能量的模拟值E50与测量值E50的差值平均值为（0.050±0.031）mm，模拟值E70与测量值E70的差值平均值为（0.042±0.026）mm，模拟值D80与测量值D80的差值平均值为（0.036±0.025）mm。

图3 在不使用脊形滤波器的情况下，质子模拟和测量相对积分深度剂量分布曲线Fig.3 Proton relative integrated depth dose distribution curves of simulations and measurements without using ripple filter

模拟能量值与系统标称能量之间的关系可以用一次函数来描述，如图4所示。本研究选择121.1 MeV的质子测量数据进行验证，并根据对应关系，应采用122.36 MeV 质子进行模拟。结果表明模拟值与测量值有很好的一致性，E50 位置偏差为0.06 mm，E70 位置偏差为0.06 mm，D80 位置偏差为0.05 mm，对比结果如图5所示。

图4 模拟-测量能量对应关系曲线Fig.4 Simulation-measurement energy correspondence curve

图5 121.1 MeV质子模拟和测量相对积分深度剂量分布曲线Fig.5 121.1 MeV proton relative integrated depth dose distribution curves of simulations and measurements

2.2 A/B型脊形滤波器展宽效果对比

图6展示模拟使用A/B 型脊形滤波器和模拟不使用脊形滤波器的相对积分深度剂量分布曲线的对比。虚线表示模拟不使用脊形滤波器的积分深度剂量曲线，红色、蓝色实线分别表示模拟使用A 型、B 型脊形滤波器的积分深度剂量曲线。可以看出，A 型、B 型脊形滤波器都将布拉格峰展宽，并且也使得相对剂量变低，布拉格峰“爆发”的路径变短。

图6 模拟使用A/B型脊形滤波器和模拟不使用脊形滤波器的相对积分深度剂量分布曲线对比Fig.6 Comparison of relative integrated depth dose distribution curves simulating with or without using an A/B type ripple filter

不使用脊形滤波器与使用A、B 型脊形滤波器束流 的E50-D50、E80-D80 和D80-D20 模 拟 值对比 表格，见于表1。对于统计的5种能量的质子，将A型脊形滤波器与B 型脊形滤波器的平均展宽值进行对比发现A 型脊形滤波器相比B 型脊形滤波器将E50-D50 平均多展宽了0.80 mm，A 型脊形滤波器相比B型脊形滤波器将E80-D80 平均多展宽了0.27 mm，A型脊形滤波器相比B 型脊形滤波器将D80-D20 平均多展宽了0.08 mm。对于48.1、104.5 和136.2 MeV 的质子，A型脊形滤波器将布拉格曲线E80-D80展宽了2.70、1.39 和1.12 倍，而B 型脊形滤波器展宽了2.23、1.28 和1.17 倍。A 型脊形滤波器对低能质子展宽效果更好。随能量升高，A 型与B 型脊型滤波器对束流的展宽程度有所下降。E50-D50 和D80-D20 的数据也有相似的规律。

表1 5档能量下不使用脊形滤波器与使用A/B型脊形滤波器E50-D50、E80-D80、D80-D20模拟值对比(mm)Tab.1 Comparison of E50-D50,E80-D80,D80-D20 simulation values under the condition of without using ripple filter and using A/B ripple filter at 5 different energies(mm)

3 讨论

本研究通过测量质子束流数据建立了质子束流的蒙特卡罗模型，并参照文献参数，设计了A、B 型两种脊形滤波器，通过蒙特卡罗模拟方法研究了A、B型两种脊形滤波器对5 档能量的质子束流的展宽能力。

上海市质子重离子医院的同步环加速器产生的质子束流，能量切换的时间约为5 s，能量切换时间是影响患者治疗使用束流时间的主要因素之一。通过脊型滤波器可以有效展宽质子束流，减少治疗计划所需能量层，从而缩短治疗时间。以一个60 层的治疗射野为例，所需束流时间约5 min，若能量层数降低1/3，则可以至少减少90 s 束流时间，从而大大提高束流利用效率。

本研究为脊形滤波器的设计提供了一些思路，研究者可在A型脊形滤波器基础上，调整宽度或厚度以寻找到展宽效果更佳的脊形滤波器结构。分析模拟获得的积分深度剂量分布曲线，可得出结论：A、B型脊形滤波器对质子束流都有所展宽，但A型脊形滤波器滤波器的展宽能力强于B 型脊形滤波器。Vogel等［9］进行了厚度分别为2、3 mm 的两种三棱柱型脊形滤波器展宽质子束流的实验，结果表明无论厚度是2 mm 还是3 mm 的三棱柱型脊形滤波器，对低能质子展宽效果显著，对高能质子展宽效果都不明显。本研究采用不同的滤波器结构，进一步论证了该观点。基于A型脊形滤波器的上述特点，其对浅表肿瘤的治疗存在优势：在低能区域可以减少能量层的使用，降低患者治疗时间；而在中、高能量区域，A 型脊型滤波器的展宽效果不明显，从而保持了中、高能质子布拉格峰末端快速跌落的特性，可以更好地保护靶区后的正常组织。初步研究表明A 型脊型滤波器在乳腺肿瘤和四肢肿瘤等浅表肿瘤的临床治疗中具有应用前景。

然而，本研究还存在着一些不足：（1）A 型脊形滤波器对束流末端的展宽效果不是十分理想，模拟获得的积分深度曲线的末端不平滑，而使用B型脊形滤波器模拟的积分深度剂量分布曲线的末端很平滑，但展宽效果不如A型脊形滤波器显著；（2）对于高能质子的展宽，两种脊形滤波器展宽效果都不明显；（3）影响脊形滤波器展宽能力的因素包括脊形滤波器的形状、宽度、厚度以及材料等，目前的研究主要针对脊型滤波器的厚度进行了调整；（4）目前本研究仅是在文献基础上，对脊形滤波器展宽布拉格峰进行模拟，其它形状的脊形滤波器展宽效果是否更好，A、B 型脊形滤波器对束斑的展宽作用以及这种展宽对靶区适形性的影响等问题，仍有待于进一步研究。基于此，质子束流脊型滤波器的临床应用，仍需进一步的验证及研究。