基于LeakyMish 流行正则化半监督生成对抗网络的图像分类模型

张鹏，魏延，胡将军

（重庆师范大学计算机与信息科学学院，重庆401331）

0 引言

随着互联网的普及和智能信息处理技术的迅速发展，大规模图像资源不断涌现，而面对海量的图像信息，如何准确地对图像进行分类成为了近几年的研究热点。图像分类就是根据图像的不同特征将不同类别的图像进行区分。常用来测试图像分类准确率的数据集有SVHN、CIFAR-10 等数据集。

机器学习方法一般分为三大类：监督学习、无监督学习和半监督学习。由于监督学习需要大量的人工标签，在实际应用中，需要消耗大量的人力财力；无监督学习是通过读取数据学习模型和规律，准确率较差；半监督学习是以少量的标签样本训练大量无标签样本，与监督学习相比较，半监督学习需要消耗的人力财力较低，且可以取得较高的准确率，因此半监督学习成为了学者们的研究热点。

在深度学习[1]中，虽然图像分类现有的方法如卷积神经网络（Convolutional Neural Networks，CNN）[2]等已经有了很高的准确率，但这些方法需要大量数据并且收敛速度较慢。生成对抗网络（Generative Adversarial Network，GAN）[3]的出现迅速被研究应用的到了各个领域，图像分类就是其中之一，生成对抗网络模型生成的样本可以弥补一些数据集，可以弥补CNN 的一些缺陷，且取得不错的准确率。

1 生成对抗网络

GAN 是Goodfellow 在2014 年提出的一种深度学习模型，GAN 的优点在于，GAN 是一种生成式模型、可以产生更加真实的样本，并且是一种无监督的学习方式训练，故在近几年引起了深度学习界的广泛关注。GAN 也因此迅速发展，不断地被改进并应用到的各个领域，如计算机视觉、文本、语音和图像等等领域。GAN 是Goodfellow 受二人零和博弈游戏启发提出的，在零和博弈游戏中，极小极大两个玩家相互竞争；而在GAN 模型中，有两模块，分别是生成器和鉴别器，故是生成器和鉴别器相互竞争。生成器通过学习真实样本生成类似真实样本的生成样本，尽可能地欺骗鉴别器，而鉴别器区分真实样本和生成样本，尽可能地不被生成样本欺骗，两者相互竞争，最终达到纳什均衡，它表述为：

其中，x 为真实图像库中的图像，Pdata为其分布，z为随机噪声，Pz为其分布，一般为高斯白噪声，D（x）是真实图像输入鉴别器后的输出概率值，G（z）是隐变量通过生成器得到的生成图像，D（G（z））是生成图像通过鉴别器后的输出概率值。生成对抗网络模型结构如图1 所示。

图1 生成对抗网络结构模型

从图1 中可以看出，原始的生成对抗网络是一个二分类模型，真实样本和生成器生成的样本传输给鉴别器，鉴别器判断是真样本还是假样本，并反馈给生成器和鉴别器，从而提高了生成器生成真实样本的能力和鉴别器判别真假的能力。

2 流行正则化半监督生成对抗网络

2.1 半监督生成对抗网络

半监督生成对抗网络（Semi-Supervised Learning with Generative Adversarial Networks，SSLGAN）[4]是Augustus Odena 提出的模型，SSLGAN 在GAN 的基础上进行的改进，并将GAN 应用到了半监督领域中，即用少量的标记样本来训练大量的无标记样本。监督学习需要大量的标记样本，而这需要消耗大量的人力和财力，故半监督学习成为重点的研究方向之一，SSLGAN也为GAN 带来了新的潜力。SSLGAN 模型结构如图2所示。

从图2SSLGAN 模型可以看出，真实样本变为了k类样本，在半监督学习遇到的都是多分类问题，故SSLGAN 模型由原始GAN 的二分类模型改进为多分类模型。k类真实样本和生成器生成的样本传输给鉴别器，鉴别器区分样本是k类中的一类真实样本还是生成器的生成样本。

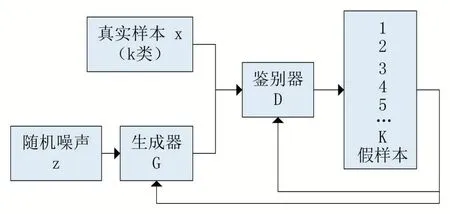
图2 SSLGAN模型结构

2.2 Improved GAN+Manifold Reg模型

Improved GAN+Manifold Reg 模型［5］是Bruno Lecouat 和Chuan-Sheng Foo 等人提出的模型。Improved GAN+Manifold Reg 模型是在知名半监督GAN 中Improved GAN［6］模型上进行改进的模型。

Bruno Lecouat 和Chuan-Sheng Foo 提出拉普拉斯范数估计可近似为：

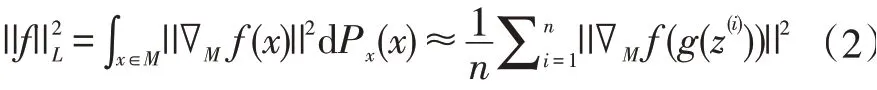
GAN 可以对图像流形进行建模[6-7]。生成器g 定义了一个图像上的流形[8]，从而计算相对于潜在表示的所需梯度，梯度是雅可比矩阵，故表示为：

J 是雅可比矩阵。

由公式（2）和（3）得公式（4）：

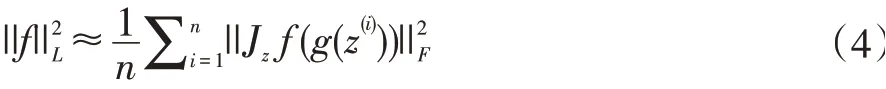
Bruno Lecouat 和Chuan-Sheng Foo 使用有限差分法来近似最终的雅可比矩阵正则化器。雅可比矩阵正则化器表示如公式（5）所示：

Bruno Lecouat 和Chuan-Sheng Foo 又将雅可比矩阵正则化器应用于半监督生成对抗网络的鉴别器中，鉴别器的损失函数如公式（6）～（8）所示：

Improved GAN + Manifold Reg 模型的鉴别器损失函数使用是上述鉴别器的损失函数，生成器使用的是Salimans 等人提出的特征匹配［5］，防止当前鉴别器过度训练。生成器的损失函数表示如公式（9）所示：

h（x）表示的鉴别器中间层的激活值。Improved GAN+Manifold Reg 模型在稳定性和准确率上都比Improved GAN 模型有了进一步的提高。

3 Improved GAN+Manifold Reg+LMM模型

针对Improved GAN+Manifold Reg 模型的学习能力，为提高图像分类的准确率，提出了Improved GAN+Manifold Reg+LMM 模型，该模型是一半监督图像分类模型。

3.1 激活函数

常用的激活函数有ReLU、LeakyReLU 等。

线性整流单元（Rectified Linear Unit，ReLU），ReLU函数的数学公式可表示为：

ReLU=max（0,x） （10）

从公式（10）可以看出，在x 轴正轴ReLU 函数为正比例函数，在x 轴负轴ReLU 函数为0。ReLU 函数可以有效的进行梯度下降和反向传播。

泄露修正线性单元（Leaky Rectified Linear Unit，LeakyReLU），LeakyReLU 函数是在ReLU 函数上进行了一个改进，LeakyReLU 函数的数学公式可表示为：

leaky 是（0，1）区间内的固定参数。LeakyReLU 函数对负值输入有很小的坡度，减少了静默神经元的出现，故效果要比ReLU 好。

然而针对激活函数的研究却一直没有停过。D Misra 提出了一种新的深度学习激活函数——Mish[9]激活函数。在D Misra 的论文中，Mish 函数在最终准确度上比Swish 和ReLU 都有提高。类似于Swish，Mish是一个平稳和非单调激活函数可以定义为：

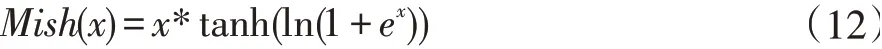
Mish 函数的图形如图3 所示。

图3 Mish函数图形

对Mish 函数进行求导，得出表达式如下：

Mish 函数导数图形如图4 所示。

图4 Mish函数导数图形

从图3 可以看出，Mish 函数在x 正半轴接近成正比例，在x 负半轴接近0-。Mish 函数表现良好正是因为函数正值可以达到任何高度，避免了由于封顶而导致的饱和，从图4 可以看出Mish 函数导数图形是光滑的，即Mish 函数以光滑的曲线，故平滑的Mish 激活函数允许更好的信息深入神经网络，从而得到更好的准确性和泛化。

针对生成对抗网络的鉴别器和生成器的激活函数进行了研究，生成器卷积神经网络的激活函数使用ReLU 函数，鉴别器则使用的是LeakyReLU 函数。由此，针对生成器的激活函数是Mish 函数，提出了激活函数LeakyReLU 函数，鉴别器的激活函数为LeakyMish函数。LeakyMish 函数表达式如下：

leaky 是（0，1）区间内的固定参数。

leaky=0.2 时，Leaky Mish 函数图形如图5 所示。

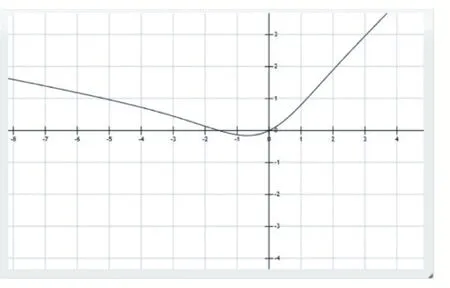
图5 Leaky Mish函数图形

对leakyMish（x）求导，得出如下表达式：

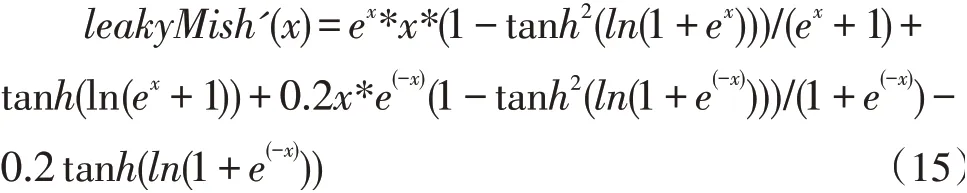
LeakyMish 函数导数图形如图6 所示。

图6 Leaky Mish函数导数图形

通过图5 发现，LeakyMish 函数也是在x 轴正轴正值比例，避免了由于封顶而导致的饱和。从图5 和图6看出LeakyMish 函数图形及其导数图形都是光滑的，从图4 和图6 可以看出LeakyMish 函数的导数图形和Mish 函数的导数图形相似，故LeakyMish 是光滑的曲线，可用做激活函数。故LeakyMish 激活函数允许更好的信息深入神经网络，从而得到更好的准确性和泛化数。

3.2 优化器

Adam［9］优化器是常用的一种优化器，它是由OpenAI 的Diederik Kingma 和多伦多大学的Jimmy Ba 提出来的。Adam 可以基于训练数据迭代更新神经网络的权重，但是Adam 在训练的初期，因为缺少数据导致方差大，学习率的方差较大，但可以控制自适应率的方差来改变效果。SGD［9］优化器另一种常用的优化器，它能够自动逃离鞍点和比较差的局部最优点，但是速度相对要慢。

因此，在选择优化器中，一个较好的优化器是能够在收敛速度和收敛效果都比较好的。SGD 优化器收敛较好，但是慢；Adam 优化器收敛较快，但容易收敛到局部解。

RAdam（Rectified Adam）[10]优化器能够在收敛速度和收敛效果都表现的比较好。RAdam 优化器是Liyuan Liu、HaomingJiang 和PengchengHe 等人提出一种新的优化器，它是经典Adam 优化器的一个新变种，在自动的、动态的调整自适应学习率的基础上进行了进一步改进，构建了一个整流器项，允许自适应动量作为一个潜在的方差的函数缓慢但稳定地得到充分表达。在某些情况下，由于衰减速率和潜在方差的驱动，RAdam退化为具有等效动量的SGD。故，RAdam 根据方差的潜在散度动态地打开或关闭自适应学习率，弥补了Adam的缺点。故，选用RAdam 优化器。

3.3 生成器和鉴别器架构

Improved GAN + Manifold Reg + LMM 模型生成器架构如表1 所示。

表1 生成器架构

从表1 展示出，生成器是一个带有批处理归一化的4 层深度卷积神经网络，前3 层网络都使用Mish 激活函数，第4 层使用Tanh 激活函数。Tanh 函数是0均值，更加有利于提高训练效率，在特征相差明显时的效果会很好，在循环过程中会不断扩大特征效果，在CIFAR-10 实验和Svhn 实验中，以不同的方式初始化鉴别器WN（WeightNorm）层的权值，故在实验中分别展示鉴别器的架构。

4 实验

4.1 实验

实验部分检验Improved GAN + Manifold Reg +LMM 模型对图像分类的能力，为了展示Improved GAN+Manifold Reg+LMM 模型对复杂数据都有较好的学习能力，实验在CIFAR-10 数据库和SVHN 数据库两个数据库上进行测试。RAdam 优化器初始学习率

设为3*10-4，正则化权值λ设为10-3，ϵ设为10-5。模型中同样使用WN、BN（BatchNorm）以及dropout 策略。实验在TensorFlow 深度学习框架实现的，在单块GPU型号为Tesla P40 上运行。

4.2 CIFAR-10实验

CIFAR-10 数据集较为复杂，数据集中的图像均为自然图像，图像中存在很多细节，而且同一种类别的不同的图像之间也有较大的差异，所以该数据集对分类模型的鲁棒性要求较高。CIFAR-10 数据集包含10 类彩色图像，图像大小为32×32，数据集有50000 个训练样本，10000 个测试样本。

鉴别器架构如表2。

表2 鉴别器架构

从表2 可以看出，鉴别器使用了带有dropout 的9层深度卷积网络和权值归一化，而9 层深度卷积网络都是用的LeakyMish 激活函数。在9 层深度卷积网络中有3 个dropout，取值分别为0.2、0.5 和0.5，提高了模型的泛化能力。初始化鉴别器WN 层的权值为96。

在实验中，Epoch 设为1300，Batch size 设为50。

CIFAR-10 实验中鉴别器的损失变化如图7 所示。

图7 CIFAR-10实验中鉴别器的损失变化

从图7 可以看出，鉴别器的损失值也是由开始的快速下降到逐渐平稳，说明鉴别器在训练时可以快速收敛并趋向稳定，鉴别器的鉴别能力在开始快速提高，然后逐渐平稳。

CIFAR-10 实验中测试集的准确率如图8 所示。

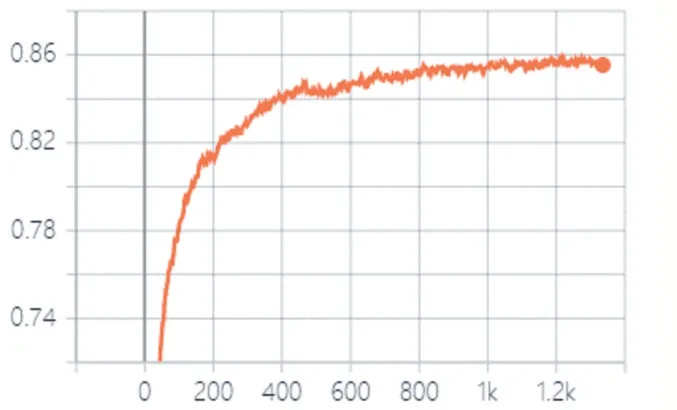
图8 CIFAR-10实验中测试集的准确率

从图8 可以看出，CIFAR-10 实验中测试集的准确率先是快速上升，然后逐渐减缓，也反映出了Improved GAN+Manifold Reg+LMM 模型收敛较快。

将Improved GAN+Manifold Reg+LMM 模型与一些知名的、准确率高的算法在CIFAR-10 数据库进行对 比，如Improved semi-GAN[13]、Improved GAN[14]等。CIFAR-10 上各种方法准确率对比如表3 所示。

表3 CIFAR-10 上各种方法准确率对比

从表3 可以看出，Improved GAN + Manifold Reg +LMM 模型在CIFAR-10 数据集中取得了较好的结果，准确率为85.75%，相比Improved GAN + Manifold Reg模型提高了0.25%。

4.3 SVHN实验

SVHN 数据库是彩色街牌号图像数据库，每张图像上都有一个或多个数字，但图像的类别以正中间的数字为基准。SVHN 数据库的图像大小为32×32，共有73257 个训练样本，26032 个测试样本。

鉴别器架构如表4。

表4 鉴别器架构

从表4 可以看出，鉴别器同样使用了带有dropout的9 层深度卷积网络和权值归一化，9 层深度卷积网络都是用的LeakyMish 激活函数。在9 层深度卷积网络中有3 个dropout，取值分别为0.2、0.5 和0.5，从而提高了模型的泛化能力。与CIFAR-10 实验不同的是初始化鉴别器WN 层的权值为64。

在实验中，Epoch 设为1300，Batch size 设为50。

SVHN 实验中鉴别器的损失变化如图9 所示。

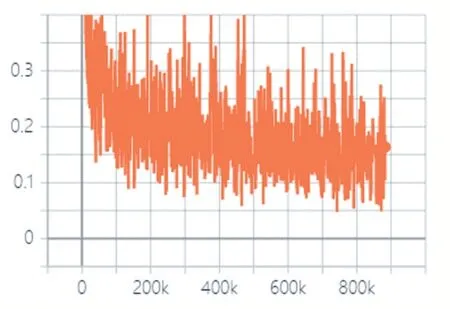
图9 SVHN实验中鉴别器的损失变化

从图7 可以看出，鉴别器的损失值是由开始的快速下降到逐渐平稳，同理，说明了鉴别器的鉴别能力在开始快速提高，然后逐渐平稳。

SVHN 实验中测试集的准确率如图10 所示。

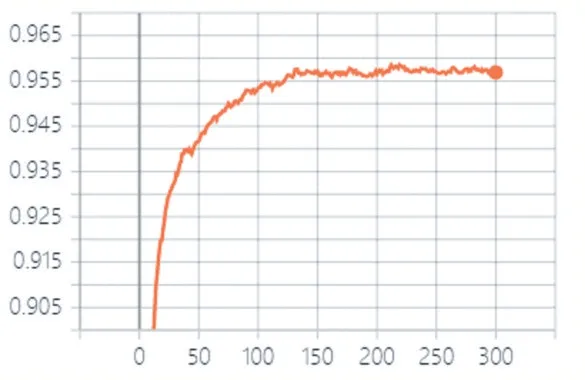
图10 SVHN实验中测试集的准确率

从图10 可以看出，SVHN 实验中测试集的准确率先是快速上升，然后逐渐减缓，也反映出了Improved GAN+Manifold Reg+LMM 模型收敛较快。

将Improved GAN+Manifold Reg+LMM 模型与一些知名的、准确率高且是在半监督领域先进的算法在SVHN 数据库进行对比，如VAT、Improved GAN 等。

SVHN 实验中多种方法准确率对比如表5 所示。

表5 Svhn 实验中多种方法准确率对比

从表5 中，可以看出，流形正则化半监督生成对抗网络在SVHN 数据集中取得了较好的结果，测试集准确率为95.74%，相比之前，提高了0.29%，准确率也比Improved semi-GAN 模型略高。

4.4 实验分析

从图7 和图9 可以得出，Improved GAN+Manifold Reg+LMM 模型收敛较快；鉴别器损失值较低，鉴别器鉴别能力较高。从图8 和图10 可以得出，测试集的准确率开始上升然后逐渐平稳，收敛较好。从表3 和表5可以得出，在多个算法对比中，Improved GAN + Manifold Reg+LMM 模型的准确率较高，效果较好。

5 结语

本文主要针对提高图像分类准确率进行了研究，提出了Improved GAN + Manifold Reg + LMM 模型，Improved GAN+Manifold Reg+LMM 模型是一种半监督生成对抗网络模型，并在CIFAR-10 实验和SVHN实验中取得较好的实验结果，在和Improved GAN、Triple GAN、Improved semi-GAN 和VAT 等经典算法对比中，Improved GAN+Manifold Reg+LMM 模型的准确率较高，在训练时模型也收敛速度较快。Improved GAN+ Manifold Reg 算法在半监督生成对抗网络中属于先进的算法，故在此基础上改进是可行的。