部分充填式钢箱-混凝土组合连续梁滑移分析
2020-06-08蒋越莫时旭郑艳韩涛
蒋越,莫时旭,2,郑艳,2,韩涛
(1.桂林理工大学 土木与建筑工程学院,广西 桂林 541004;2.广西岩土力学与工程重点实验室,广西 桂林 541004)
0 引 言
钢箱-混凝土组合连续梁是钢箱梁与混凝土翼板通过剪力连接件连接在一起,并协同工作的一种新型梁,可以充分发挥钢梁受拉性能和混凝土板受压强度的优势,其整体受力性能要明显优于二者受力性能的简单叠加。钢箱-混凝土组合连续梁承载力高、截面高度小、整体稳定性好,因此,在国内外得到广泛的应用与研究。在荷载作用下,钢箱梁与混凝土板打破整体的变形协调限制,产生轴向剪力,从而使组合梁存在相对滑移。
钢箱-混凝土组合连续梁界面与连接件的分析属于接触非线性问题,是研究组合连续梁相对滑移的关键,国内外学者均对此进行了大量研究。A Morassi等[1]通过4根钢-混凝土组合的自振模态试验发现,组合梁的自振特性与抗剪连接件的损伤之间有极大的关系;CHEN S M[2]通过试验研究发现,连续组合梁的滑移与材料有关,进一步编写了连续组合梁材料非线性的程序;J.G.Ollgaard等[3]对栓钉的抗剪承载能力进行了深入研究,建立的栓钉抗剪连接模型被各国规范采用;石卫华等[4]对栓钉抗剪连接件的承载能力进行了可靠度分析,并提出栓钉抗剪连接承载能力的修正公式;杨勇等[5]分析了端部混凝土对单孔连接件极限承载力的贡献,并提出连接件抗剪承载能力的计算模型;王景全等[6]通过简支钢-混凝土组合梁的静力加载试验,得出了截面滑移对组合梁的力学性能的影响。
目前研究中对栓钉的抗剪连接度和布置没有明确的标准,针对此问题,设计了3片不同抗剪连接度试验组合梁进行试验,同时利用ANSYS建模进行分析。探讨不同抗剪连接度对部分充填式窄幅钢箱-混凝土组合连续梁的极限承载力、挠度、滑移的影响,并给出适合于部分充填式窄幅钢箱-混凝土组合连续梁的最佳抗剪连接度和栓钉布置方式。
1 试 验
1.1 试验梁参数
设计了3根充填式窄幅钢箱-混凝土组合连续梁试件。试验梁总长L=6 400 mm,共有两跨,每跨3 000 mm,梁高420 mm;混凝土翼板厚为120 mm,宽1 000 mm;钢箱梁采用Q235钢板焊接而成,腹板高300 mm,顶板和底板宽度均为220 mm,厚10 mm。混凝土力学性能参数见表1,钢材力学性能参数见表2。在负弯矩区部分充填核心混凝土,充填率为50%,组合连续梁负弯矩区横截面如图1所示。钢箱梁与混凝土板之间采用13 mm的4.8级普通栓钉连接,抗剪连接度通过栓钉间距大小调节。栓钉布置参数见表3。

表2 钢材力学性能参数

图1 组合连续梁负弯矩区横截面图
Fig.1 Section diagram of negative moment zone of the composite beam

表3 栓钉布置参数
1.2 试验装置
试验装置包括反力架、液压千斤顶、应变采集系统、压力传感器和显示千分表。采用静力加载方式,试验装置如图2所示。利用反力架通过梁跨中位置的2个液压千斤顶两点对称施加在试验梁上。施加力大小由2个压力传感器显示。应变采集系统按荷载逐级采集应变数据,应变箱的补偿片与同尺寸的钢箱-混凝土组合连续梁连接,利用电桥加减特性使2片试验梁进行相互温度补偿,从而减小试验误差。在试验梁的支座L/4,L/2,(3L)/4截面混凝土翼板与钢箱界面处分别安置千分表,用于测量翼板、支座位移与钢箱的相对滑移。

图2 加载装置
1.3 结果与分析
1.3.1 荷载-挠度曲线
为考虑不同抗剪连接度对部分充填式窄幅钢箱-混凝土组合连续梁变形能力的影响,选取试验梁荷载-跨中挠度关系曲线进行对比研究,如图3所示[10]。3片试验梁PFSCB1、PFSCB2与PFSC-B3抗剪连接度分别为1.0,0.75,0.5。开始加载时,连续组合梁翼板与钢箱梁交界面之间产生的滑移量很小,连续组合梁挠度值大小可以忽略不计,3片试验梁的挠度随荷载变化趋势基本接近,均为线性变化,此时组合梁处于弹性阶段。荷载继续增大时,组合梁受到的剪力较大,钢箱梁核心混凝土出现脱空现象,钢箱发生局部屈曲,剪力连接度较低的试验梁产生的滑移量开始增大,从而使连续组合梁截面曲率增大,呈非线性,组合梁进入弹塑性阶段。当荷载继续增大接近极限荷载时,试验梁PFSCB3挠度骤增,这是因为局部屈曲导致刚度降低,同时组合梁受到的剪力过大导致栓钉剪断,因此,试验梁的承载能力受界面滑移影响较大,试验梁PFSCB1为高抗剪连接,受到的影响较小。组合梁在进入弹塑性阶段以后,挠度发展很快,增长幅度约为弹性阶段的2倍,组合梁展现出相当好的延性。

图3 试验梁荷载-跨中挠度关系曲线
1.3.2 荷载-滑移关系曲线
连续组合梁中混凝土板和钢箱梁通过栓钉抗剪连接件的作用形成一个整体,协同工作,受到连续组合梁传递过来的水平剪力作用时,栓钉会发生形变,使得钢箱梁与翼板交界面之间出现相对滑移[11]。相对滑移的出现降低了试验梁的刚度,使其曲率和挠度变大,影响整体受力性能,因此,为研究部分充填式窄幅钢箱-混凝土组合连续梁的滑移变化情况,绘制荷载-滑移曲线图和试验梁延梁纵向滑移分布图,如图4所示。从图4可以看出,开始加载时,3片连续试验梁的滑移值均较小,界面滑移值曲线基本呈线性变化,反映出弹性阶段试验梁中混凝土板和钢箱梁的整体工作性能良好。随着荷载不断增大,试验梁剪力增大,钢梁与翼板自然黏结力破坏,栓钉承担交界面剪力作用而发生形变,相比试验梁PFSCB2与PFSCB1,试验梁PFSCB3抗剪连接度较小,滑移值增长较快。当连续组合梁进入弹塑性工作阶段,钢箱承受较大弯矩、剪力而出现局部屈曲,挠度增大明显,交界面之间滑移曲线呈非线性变化。随着荷载持续增加,试验梁PFSCB3的滑移值急剧增加,曲线开始变平,抗剪连接度较小的组合梁中栓钉开始被剪断。从试验过程可以看出,塑性破坏阶段时试验梁PFSCB2与PFSCB1延性较好,因此,在较高剪力连接度下,部分抗剪设计对连续组合梁的受力性能和抗弯刚度影响不是很大。

图4 试验梁荷载-跨中相对滑移曲线
2 有限元模型建立与求解
2.1 单元类型选择
运用有限元软件ANSYS对钢箱-混凝土组合连续梁进行建模,有限元模型如图5所示。钢箱梁与混凝土均采用三维实体单元,钢箱梁采用Solid45模拟;混凝土采用Solid65单元模拟,与Solid45相比,增加了材料非线性的处理,能有效模拟出混凝土的开裂、压碎、塑性变形和徐变,还可模拟钢筋的拉伸、压缩、塑性变形和蠕变;钢箱内部分填充的混凝土与钢箱的连接采用Link10单元模拟,此单元能有效模拟轴向受压和受拉的全过程。栓钉采用combin39单元,直接在钢箱梁和混凝土的两个重合点上建立弹簧节点,然后定义其荷载-位移曲线。本文主要研究钢梁与混凝土的滑移,建模时只需模拟组合梁的栓钉作用,钢箱梁与混凝土板的黏结作用很小,不予考虑。

图5 钢箱-混凝土组合连续梁有限元模型
2.2 材料本构关系
2.2.1 混凝土本构关系
该单元材料的非线性关系主要通过定义混凝土单轴受拉、受压应力-应变本构关系曲线实现。根据《混凝土结构设计规范》[7]中定义的混凝土受压本构关系确定本文的本构关系,混凝土的应力-应变曲线出现抛物线形的上升、下降段,如图6所示,上升段计算公式为
(1)
下降段计算公式为
(2)
式中:ε为混凝土轴向应变;ε0为混凝土最小轴向应变,取0.002;εu为混凝土最大轴向应变,取0.003 5;σ为混凝土应力,MPa;σ0为混凝土的峰值应力,σ0=0.85R,R为混凝土立方抗压强度,MPa。

图6 混凝土材料应力-应变曲线
钢箱内充填混凝土后,混凝土的受力情况与方钢管混凝土构件类似,在文献[8]提出的方钢管核心混凝土应力-应变关系基础上引入配钢指数λ进行修正,修正后的表达式为
(3)
式中:θ为界限底角,(°);fck为素混凝土抗压强度,MPa;As为钢箱截面面积,mm2;Ac为钢箱内核心混凝土截面面积,mm2;fsy为钢箱的抗压强度,MPa;fcy为钢箱内核心混凝土的抗压强度,MPa。
2.2.2 钢材本构关系
连续梁中钢箱板材的SHELL181单元和钢筋的LINK8单元中有关钢材的弹性模量、泊松比、屈服强度等数值通过实常数输入。采用钢结构设计规范[9]定义其本构关系,钢材应力-应变曲线如图7所示,其应力-应变公式为
(4)
式中:σs为钢材应力,MPa;fy为屈服强度,MPa;ε为钢材轴向应变;εy为钢材进入屈服阶段的轴向应变;εt为钢材进入强化阶段的轴向应变,取0.002 8;Es为钢材的弹性模量,MPa;E′为钢材强化阶段的弹性模量,E′=0.01Es.
2.2.3 栓钉本构关系
栓钉将连续组合梁翼板受到的纵向剪力传递给钢梁,同时抵抗2种材料在受力过程中的变形从而出现掀起现象。根据栓钉试验结果,选取荷载-位移曲线作为其本构模型,F-D曲线如图8所示,其中F为荷载,D为位移。

图7 钢材应力-应变曲线
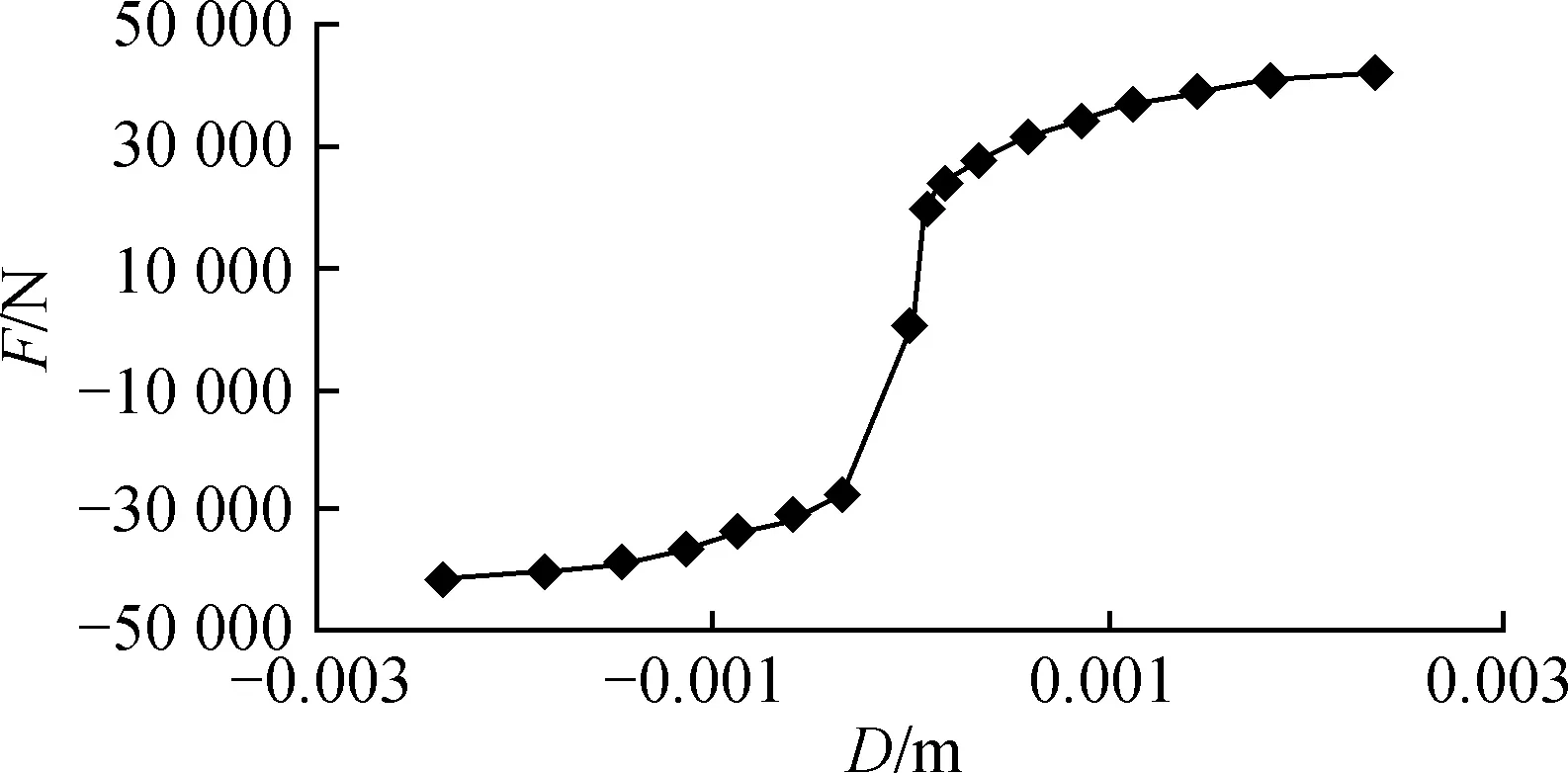
图8 栓钉荷载-位移曲线
2.3 模型求解
由于钢箱-混凝土组合连续梁模型的复杂性,先建立钢箱、混凝土翼板、钢筋等部分单元,然后将各部分组合为整体模型[12-13]。根据试验设计,建模时钢箱-混凝土连续组合梁(x,y)方向固定,组合梁中部(x,y,z)方向固定。为了避免支座和加载点因应力集中使试验梁突然破坏导致计算不收敛,在加载点设置垫块与翼板连接,在支座处设置垫块与底板连接。为确保计算结果的正确性,采用合理的收敛准则。对于钢箱-混凝土结构,混凝土材料的性质比金属材料复杂,因而在钢箱-混凝土结构的非线性分析中,混凝土强度准则的建立至关重要。本文采用Willan-warnke原则,张开裂缝的剪力传递系数βt影响比较大,此模型βt=0.3,闭合裂缝的剪力传递系数βc=0.95。考虑开裂后慢慢释放拉应力,以助吸收,拉应力释放系数Tc=1。
3 结果与分析
3.1 滑移与挠度分析
为研究连续组合梁的实际受力性能和变形情况,绘制纵向滑移分布图和荷载-跨中挠度图,如图9~10所示。
从图9可以看出,在加载过程中,以跨中为对称原点,向边跨延伸同等距离的滑移值呈反对称关系。在距跨中距离-1.5~1.5 mm的斜率很大,滑移增量较大,随着不断向两跨延伸,离梁跨边缘越近,滑移增量上升趋势越平缓,斜率不断减小,说明负弯矩区的抗剪连接度对钢箱-混凝土连续组合梁影响比较大。从图10可以看出,试验值比有限元模拟结果大,且有限元模拟曲线比试验值圆滑,这是因为试验梁在浇筑凝结时温度引起了收缩,混凝土板产生小裂缝。对于这些初始缺陷很难在有限元模拟中进行添加,因此,模拟结果精度低于试验值。经有限元曲线与试验曲线对比可知,有限元模拟结果与试验值相差不大,此模型能真实反映出连续组合梁的实际受力性能和变形情况。

图9 纵向滑移分布曲线
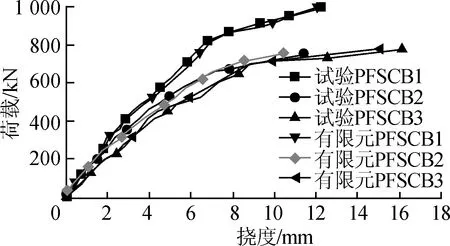
图10 荷载-跨中挠度曲线
3.2 局部屈曲分析
为研究试验过程中连续组合梁试件出现腹板局部屈曲现象,绘制了1/2试验组合梁腹板局部屈曲云图与有限元图形对比分析。有限元组合梁腹板局部屈曲云图和试验组合梁腹板局部屈曲云图如图11~12所示。从图11~12中可以看出,组合梁腹板在塑性区域内出现了局部屈曲,形成斜向屈曲波,该区域位于最大正弯矩至反弯点区间内,以剪切屈曲为主。负弯矩区未出现局部屈曲,说明负弯矩区下箱室充填混凝土可以有效分担钢箱腹板承受的压应力,减小屈曲的可能性,并限制了钢箱腹板的内屈。

图11 有限元组合梁腹板局部屈曲云图

图12 试验组合梁腹板局部屈曲云图
3.3 抗剪连接度参数分析
通过本文建立的有限元模型模拟了7片不同抗剪连接度的部分充填式钢箱-混凝土组合连续梁[14-17]。模型编号SC1~SC7的抗剪连接度分别为1.6,1.4,1.2,1.0,0.8,0.6,0.4,有限元模型梁荷载-跨中相对滑移图如图13所示,从图13中7条曲线对比可以看出,试验梁在受力过程中,从弹性阶段到弹塑性阶段延性较好,滑移值没有出现较大突变,塑性阶段滑移值骤增,交界面的塑性铰慢慢形成,使连续组合梁交界面剪力出现重分布。抗剪连接度大小在弹性工作状态反映不是很明显,抗剪连接度较大时,组合梁整体性好,荷载-滑移曲线较为均匀,在塑性阶段的刚度和变形能力更好。有限元模型梁抗剪连接度-最大滑移如图14所示。当抗剪连接度从0.4增加到1.6时,界面最大滑移量从4.25 mm减小到1.78 mm,说明交界面滑移随着抗剪连接度增大而减小。抗剪连接度在0.4~1.0时,组合梁的最大滑移值急剧增长,增量值为2.15 mm;在抗剪连接度在 1.0~1.6时,组合梁的最大滑移值增长缓慢,增量值为0.32 mm。抗剪连接度对组合梁的延性和承载能力有一定影响,随着抗剪连接度增加,最大滑移量减少,抗剪连接度超过1.0后滑移量改变不明显,说明栓钉在抗剪连接度为0.4~1.0时抗剪效果发挥比较充分。

图13 有限元模型梁荷载-跨中相对滑移关系曲线
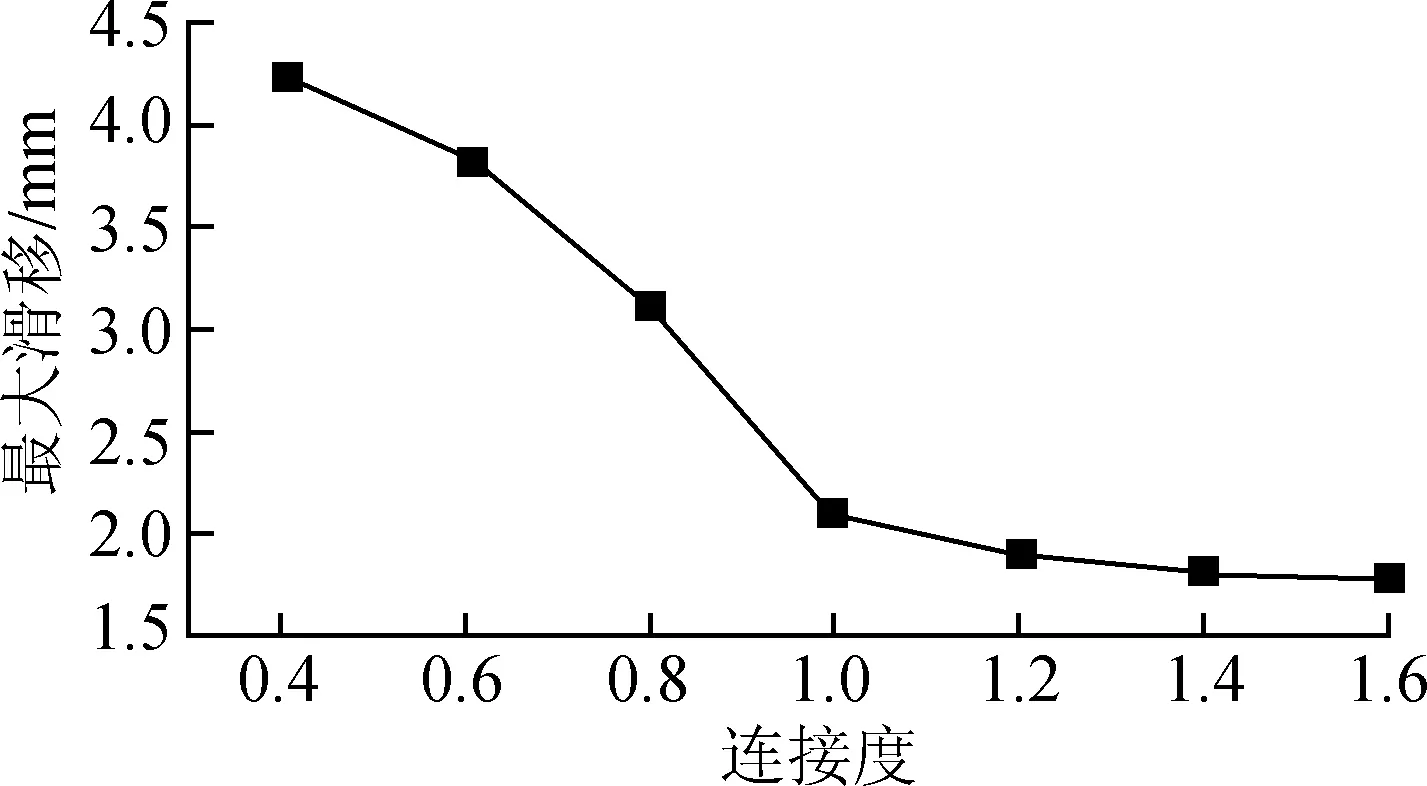
图14 有限元模型梁抗剪连接度-最大滑移关系曲线
4 结 论
(1)由试验数据分析可知,部分抗剪连接组合梁延性较好。抗剪连接度较低时,截面滑移对钢箱-混凝土连续组合梁的刚度和承载能力的影响较大,高抗剪连接度对其影响较小。
(2)经有限元分析可知,该模型能准确地模拟部分充填式窄幅钢箱-混凝土组合连续梁的受力性能。组合梁负弯矩区的抗剪连接度对钢箱-混凝土连续组合梁影响比较大,正弯矩区可以合理减少栓钉的布置数量,增大布置间距,经济效益更佳。
(3)钢箱-混凝土连续组合梁的界面相对滑移与抗剪连接度有关,抗剪连接度越大,滑移值越小,组合梁的抗弯和抗剪承载力越高。在满足刚度和承载力的情况下,可在0.4~1.0内适当调整抗剪连接度,使栓钉连接效果最佳。
