融合语义相似度的矩阵分解推荐算法
2020-06-08闵潞王根生黄学坚
闵潞,王根生,,3,黄学坚
(1.江西财经大学 人文学院,江西 南昌 330013;2.江西财经大学 计算机实践教学中心,江西 南昌 330013;3.江西财经大学 国际经贸学院,江西 南昌 330013)
0 引 言
推荐算法是解决网络信息过载问题的一种典型技术,在网络媒体、电子商务、新闻广告等领域均得到了广泛应用[1]。目前,推荐算法根据推荐引擎的不同主要分为3类,即基于内容过滤推荐、协同过滤推荐和混合推荐[2]。协同过滤推荐算法基于用户历史行为数据,没有领域限制,是目前应用最为广泛的一种推荐算法,其主要分为基于用户(user-based CF)的协同过滤、基于项目(item-based CF)的协同过滤和基于模型(model-based CF)的协同过滤。基于用户和项目的协同过滤推荐算法面对用户历史评价矩阵数据稀疏时无法起到较好的推荐效果[3],基于模型的协同过滤使用机器学习的算法思路进行建模,可在一定程度上解决矩阵稀疏问题[4],矩阵分解推荐算法就是一种基于模型协同过滤的典型算法[5]。
矩阵分解推荐算法只利用用户-项目评价矩阵,没有考虑其他因素,导致推荐结果准确率不高,针对这个问题,国内外不少学者提出了改进方案。如文献[6]提出一种基于属性耦合的矩阵分解方法,将项目属性信息合并到矩阵分解模型中;文献[7]引入用户间的信任关系,提高了矩阵分解推荐算法的性能;文献[8]在利用用户-项目评价显式信息的基础上,加入其他的隐式信息(如浏览、购买和点击历史等);余永红等[9]利用社交网络信息计算用户的社会地位,把用户的社会地位融合到矩阵分解推荐算法之中;李昆仑等[10]提出一种近邻用户影响力的数学模型,考虑近邻用户对目标用户的影响,并把这个模型整合到矩阵分解推荐算法中;文凯等[11]提出一种融合社交网络和用户间兴趣偏好相似度的正则化矩阵分解推荐算法。上述研究结果发现,引入用户或项目的额外相关信息是目前改进矩阵分解推荐算法的主要路径。随着知识图谱技术的发展,目前业界已经有大量开放的语义知识数据,如通用知识图谱Freebase、OpenKN和DBpedia,特定领域知识图HerbNet(中医领域)、WolframAlpha(数学领域)和BMKG(影视领域)等。通过知识图谱表示学习算法可以将推荐对象所处领域的语义数据嵌入到一个低维语义向量空间,所以本文提出一种融合语义相似度的矩阵分解推荐算法,把推荐对象间语义相似度融入矩阵分解的目标优化函数中,弥补矩阵分解推荐算法没有考虑推荐对象本身特征的不足。
1 理论基础
1.1 矩阵分解推荐算法
矩阵分解推荐算法(FunkSVD)通过用户-项目评分矩阵分解出两个低维的用户和项目特征矩阵,利用这两个矩阵去拟合用户对项目的评分,并对未评分项目进行预测。矩阵分解表示为
R≈UVT,
(1)
式中:R为用户-项目实际评分矩阵;U∈Rm×d为分解出的用户特征矩阵;V∈Rn×d为分解出的项目特征矩阵;m,n分别为用户和项目的个数,d为用户和项目特征维度。
用户i对项目j的预测评分计算式为
(2)
式中:Ui为用户i的特征;Vj为项目j的特征。
为使式(1)最大程度拟合用户-项目的真实评分数据,使用线性回归的思路,建立目标优化函数,具体为
(3)

使用梯度下降法进行目标优化函数(3)的求解,具体为
(4)
(5)
Ui=Ui-α[∂J/(∂Ui)],
(6)
Vj=Vj-α[∂J/(∂Vj)],
(7)
式中,α为学习率。
基于FunkSVD算法,文献[12]提出一种改进的Biased MF算法,Biased MF在目标优化函数(式(3))中引入全局平均分项、用户偏置项(用户评价平均分与全局平均分差值)和项目偏置项(项目所得平均分与全局平均分差值),最终目标优化函数为
(8)
式中:μ为全局平均分项;αi为用户i偏置项;βj为项目j偏置项。
Biased MF用户i对项目j预测评分计算式为
(9)
1.2 知识图谱分布式表示学习
Google在2012年提出了知识图谱概念,用于构建其下一代语义智能搜索引擎。知识图谱使用“实体-关系-实体”三元组描述现实世界中的实体和实体之间的关系,通过关系构成网状的知识结构[13]。知识图谱分布式表示学习对知识图谱中的实体和关系进行分布式表示,得出包含语义关系的低维向量表示[14]。TransE模型[15]因参数简单,计算复杂度低,在大规模知识图谱上性能显著,是目前主流的知识图谱分布式表示学习模型[16]。对于每个三元组(h,r,t),其中h,t分别为头实体和尾实体,r为头尾实体间的关系,TransE模型把h,t和r分别表示为嵌入向量vh,vt和vr,vr为向量vh和vt间的平移,也称为向量vh到vt的翻译,三者之间的关系为
vh+vr≈vt,
(10)
TransE模型要使公式(10)无限接近,之间的误差越小,说明头尾两个实体间越可能存在关系r,所以TransE模型的损失函数为
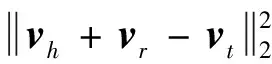
(11)

f(vh′,vr,vt′)+γ),
(12)
式中:S为所有三元组集合,称为正样本;S′为集合S的负采样,即对S中每个存在的三元组随机替换掉其头实体或尾实体,得到一个新的三元组,且该三元组不属于S;γ为正负样本间的距离。
TransE模型没有区分不同关系下的实体,在处理复杂关系的知识图谱时存在不足,针对这个问题,文献[17]提出了TransR模型,把实体和关系嵌入到不同的空间中,在对应的关系空间中实现实体表示,其损失函数为

(13)
式中:Mr为关系r的投影矩阵;vhMr为实体向量vh投影到关系r的空间。
2 融合推荐算法
针对矩阵分解推荐算法只利用用户-项目评价矩阵,没有考虑项目本身的内涵特征知识,导致推荐结果不佳的问题,本文提出一种融合语义相似度的矩阵分解推荐算法,把推荐对象间语义相似度融入矩阵分解的目标优化函数中,从语义视角弥补矩阵分解推荐算法没有考虑推荐对象本身内涵特征的不足,算法流程如图1所示。
算法流程分为4步,即语义向量表示、项目语义相似度计算、融合矩阵分解和推荐列表生产。
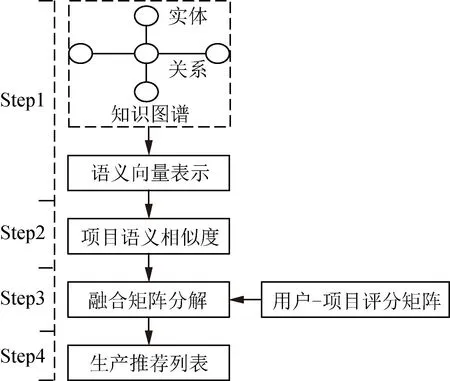
图1 算法流程图
2.1 语义向量表示
根据知识图谱分布式表示学习算法,得出推荐对象所属领域中所有实体和关系的向量表示,在实体向量中筛选出推荐对象的实体表示。该推荐对象的向量表示融合了整个领域中和其有关的实体知识,所以该向量表示包含了推荐对象上下文语义知识。推荐对象实体表示为一个d维语义向量,即
Ii=(E1i,E2i,…,Edi)T,
(14)
式中:Ii为项目i的语义向量;Eni为第n维上的值。
2.2 项目语义相似度
相似度计算主要有余弦相似度、皮尔逊相似度、Jaccard 相似度、对数似然相似度、欧式距离相似度。知识图谱分布式表示学习算法训练时损失函数是基于欧式距离,为了保持一致性,项目语义的相似度同样采用欧式距离作为衡量,计算式为
(15)
将其规约到(0,1]之间,规约计算式为
sim(i,j)=1/[1+d(Ii,Ij)],
(16)
sim(i,j)值越大,说明项目i和j语义越相近。
2.3 融合矩阵分解
融合项目语义相似度的矩阵分解算法的思想是语义相近的项目,其特征向量也应该相似,所以基于这思想,把项目语义相似度融合到Biased MF矩阵分解的目标优化函数公式(8)中,融合后的目标优化函数为
(17)
2.4 推荐列表生产
融合矩阵分解出两个低维的用户特征矩阵和项目特征矩阵,利用式(9)计算预测评分,基于预测评分越高,用户对其越感兴趣的原则,设置一个阈值,把大于该阈值的预测评分项目推荐给用户。
3 实验与分析
3.1 实验数据
选取电影推荐作为研究对象,实验数据来源于豆瓣影评数据,数据包含 7 815个用户对1 593部电影的214 920条评论。用户对电影的喜爱程度通过其对电影的星级评价衡量,星级分为1~5星,星级越大,说明用户对该电影越喜爱。本实验把4~5星标注为用户喜爱的电影,1~3星标注为用户不喜爱的电影。
本实验选用清华大学知识工程试验研究室发布的最新双语影视知识图谱(BMKG)[18],该知识图谱包含72万多个和影视相关的实体,91个属性,1 300多万条三元组,融合了豆瓣电影、百度百科和LinkedMdb等多个中英文影视数据。为了减少知识图谱分布式表示学习算法的训练时间,文本从BMKG中只抽取出和实验数据相关的知识。
3.2 评价指标
本实验使用准确率(Precision),召回率(Recall),覆盖率(Coverage)3个指标进行算法性能衡量,计算式分别为
Precision=TP/(TP+FP),
(18)
Recall=TP/(TP+FN),
(19)
Coverage=Nd/N,
(20)
式中,TP,FP,FN为混合矩阵中的值,具体如表1所示;N为实验中所有电影种类个数;Nd为推荐算法给出的电影种类数目。覆盖率越高,说明算法对冷门物品越具有很好的推荐能力,推荐结果具有多样性和新颖性。
为了对算法性能进行更精准的衡量,本文使用k-交叉验证的方式进行验证,k值取5,即随机把试验数据均分成5份,每次挑选其中1份作为测试集,其他4份作为训练集,一共进行5次测试,使用5次测试的平均值作为算法最终评价。
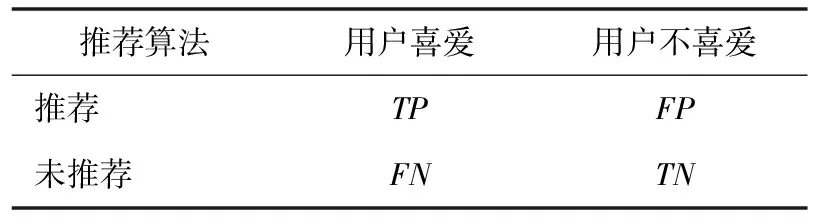
表1 混合矩阵
3.3 结果及分析
实验具体步骤如下。
Step1 根据影视知识图谱(BMKG)抽取和实验数据相关的知识。
Step2 使用知识图谱表示学习算法TransR对抽取的知识进行训练,得出电影实体的语义向量表示。
Step3 根据训练数据集构建用户-电影评分矩阵。
Step4 根据电影的语义向量,计算电影间的语义相似度,具体计算见公式(16)。
Step5 结合用户-电影评分矩阵和语义相似度进行融合矩阵分解,目标优化函数见公式(17)。
Step6 根据 Step5得出的结果,对测试数据集进行预测评分,具体计算见式(9),并且预测评分≥8分的电影放入推荐列表。
Step7 统计测试数据集的准确率,召回率,覆盖率3个指标。
Step8 改变训练集和测试集,重复Step3~Step7的实验过程,一共重复5次。
Step9 统计5次实验的平均准确率,召回率和覆盖率。
3.3.1 电影实体语义向量不同维度的实验对比
在进行知识图谱分布式表示时,不同的电影实体向量表示维度会对实验结果产生一定的影响,所以设置维度50,100,150,200共4组对比实验,实验过程中的其他关键参数如表2所示,实验结果如图2所示。

表2 实验关键参数设置

图2 电影实体语义向量不同维度下的实验结果对比
通过图2可以看出,当知识图谱分布式表示算法的实体维度设定为100时,本文算法的准确率、召回率、覆盖率相对较好。
3.3.2 不同用户和电影特征维度的实验对比
在进行矩阵分解时需要设定用户和电影的特征维度d,设为10,20,30,40,50,60,70,80,90,100共10组实验进行对比,电影实体语义向量维度设为100,其他参数和表2保持一致,实验结果如图3所示。

图3 用户和电影特征不同维度的实验结果对比
由图3可知,当矩阵分解出的用户和电影维度为80时,算法的准确率、召回率、覆盖率较好。
3.3.3 不同融合系数值的实验对比
式(17)中的融合系数λ2控制语义相似度在整个算法中所占的比例,本次实验设为0,0.5,1.0,1.5,2.0共5组λ2值,进行实验对比,电影实体语义向量维度都设为100,用户和电影特征维度设为80,其他参数和表1保持一致,实验结果如图4所示。

图4 不同融合系数的实验结果对比
当融合系数为0时,本文算法退化成Biased MF矩阵分解推荐算法,当融合系数不为0时,即在Biased MF算法中融合了电影的语义相似度。通过实验结果可以发现,该融合算法提高了Biased MF矩阵分解推荐算法的准确率、召回率和覆盖率,并且当融合系数为1.5时相对效果最好。
3.3.4 和其他矩阵分解推荐算法的实验对比
为了进一步验证本文算法的有效性,把本文算法和文献[12]提出的引入偏置的矩阵分解推荐算法(Biased MF)、传统矩阵分解推荐算法(FunkSVD)进行实验对比,本文算法的实体语义向量维度设为100,融合系数λ2设为1.5,其他参数和表1保持一致,实验结果如图5所示。
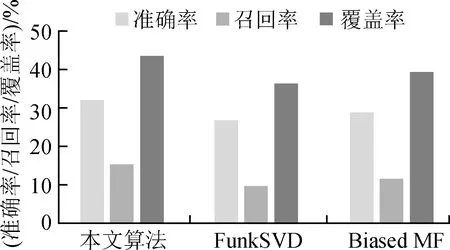
图5 不同矩阵分解推荐算法的实验结果对比
通过图5可以看出,本文算法和Biased MF相比于FunkSVD,具有更高的准确率,召回率和覆盖率,本文算法也比Biased MF算法的准确率,召回率和覆盖率高。
4 结 语
基于矩阵分解的推荐算法,在一定程度上解决了协同过滤中矩阵稀疏问题,但算法仅利用了用户-项目评价矩阵,没有考虑项目的额外相关信息,导致推荐结果不够准确。因此,本文提出一种融合语义相似度的矩阵分解推荐算法,通过知识图谱分布式表示学习算法得出项目的语义相似度,把该语义相似度融合到矩阵分解的目标优化函数中,使语义相似的项目特征向量也相近,并且通过实验证明了本文算法的有效性。虽然本文算法对传统矩阵分解推荐算法进行了部分改进,但还存在一定的不足:一方面是算法依赖于开源的知识图谱,导致算法具有一定的领域限制;另一方面,当面对海量数据时,矩阵分解的效率低;此外,算法也没有考虑到用户兴趣漂移和数据时效性问题,这些都是下一步值得研究的地方。
