考虑注浆圈情况下的任意形状隧道渗流场研究

2020-06-08李杰莫海强

铁道科学与工程学报 2020年5期

李杰，莫海强

李杰1，莫海强2

(1. 中冶(贵州)建设投资发展有限公司，贵州贵阳 550009；2. 中南大学土木工程学院，湖南长沙 410075)

对于水下隧道目前多采取“堵水限排”的处理方法，通过注浆和设置排水衬砌来减小隧道渗水量和降低衬砌所承受的水压。为了适应各种工程建设的需要，非圆形的隧道在工程实际中很常见，但目前对于考虑注浆圈情况下非圆形隧道的渗流场研究却很少。结合复变函数中的保角变换方法，推导毛洞在注浆圈和衬砌共同作用下水下任意形隧道渗流场的解。并通过FLAC3D本例解相比较，证明了本文的有效性，为实际的工程需要提供了一种快速、准确的方法。

注浆圈；任意形状；隧道；渗流场；保角变换

对于水下圆形隧道考虑注浆圈和衬砌作用下的渗流场问题，有许多国外学者对其多有研究[1−4]。王秀英等[5]利用竖井理论求出无限空间中高水压山岭隧道的渗流场解。杜朝伟等[6]结合复变函数和无限含水层竖井理论求得圆形隧道加注浆圈和衬砌作用下的渗流场。童磊等[7]运用保角变换的方法将地表、隧道边界和衬砌映射为同心圆区域，求得考虑衬砌情况下的渗流解，但是没考虑注浆圈。熊浩等[8]同样采用复变函数法和流量连续条件，考虑土层、岩层及注浆圈和衬砌等不同介质下渗流场。应宏伟等[9]利用镜像法，采用“源−汇”理论，通过渗流场叠加求得考虑注浆圈与衬砌共同作用下的解析解。实际工程中，水下隧道存在许多非圆形隧道注浆加固堵水的情况，因此本章主要对于非圆形水下隧道及其考虑注浆情况下稳定渗流场进行分析，采用保角变换方法，推导了非圆情况下渗流场的解，并以椭圆形孔口为例，通过数值模拟加以验证解的正确性，可为水下任意形状断面隧道的排水系统设计提供一定的参考依据。

1 基本假设

计算模型图如下：假定水面以下介质为围岩、注浆圈、衬砌。取水面为位势零面，水面高于地表围岩的深度为h水平面距地表，为隧道中心埋深，为隧道注浆圈高度的一半，为注浆圈的厚度。

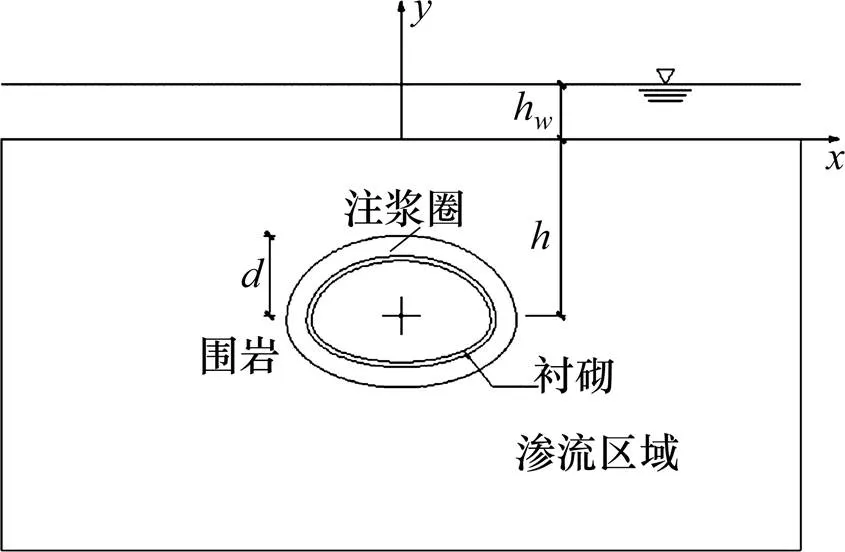
图1 水下隧道示意图

作出如下的基本假设：1) 围岩、注浆圈、衬砌为均匀且各向同性的介质；2) 地下水水源充足不可压缩，隧道排水不影响现有的地下水位；3) 隧道横截面为任意形，注浆圈与衬砌的形状与隧道横截面形状一致，纵向上满足平面应变的条件；4) 渗流服从达西定律，并假设隧道内壁均匀渗水，围岩内渗流方向以径向渗流为主。

如图2中所示，各个面的压力水头，0为隧道衬砌内壁的压力水头，因为考虑隧道排水，则0=0；1为衬砌与注浆圈交界面的压力水头；h为注浆圈与围岩界面的压力水头，h为水面高于地表围岩的深度，即围岩表面的压力水头。

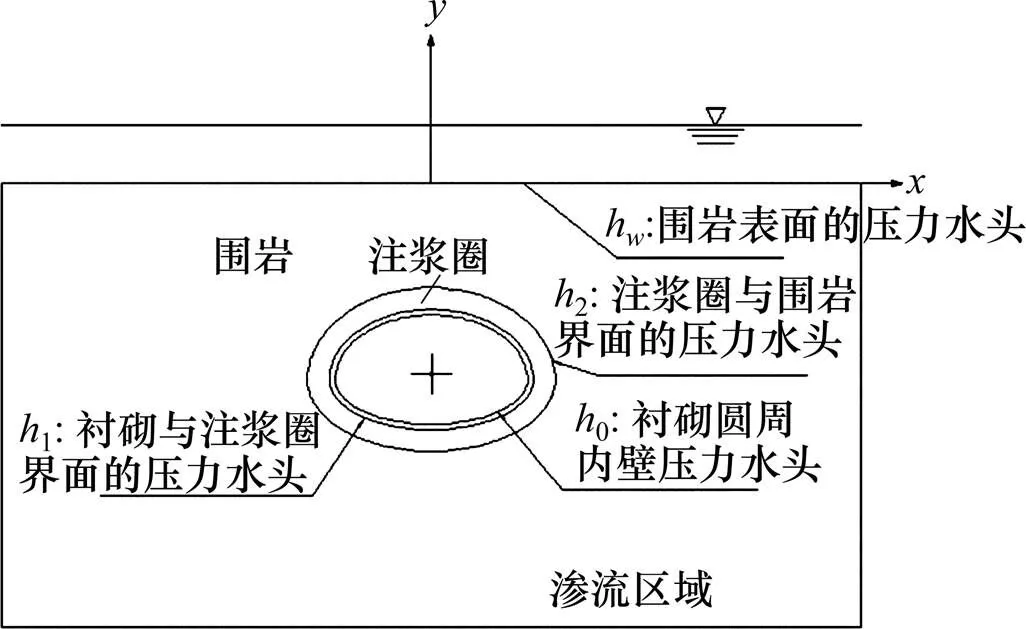
图2 各接触面压力水头示意图

2 基本方程及模型分解

根据水下渗流的连续性原理，隧道周边二维稳定渗流遵循拉普拉斯方程：

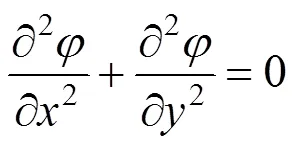
为了求解上式，由于在原平面中求解非常困难，需要通过保角变换，将模型边界简化为比较简单形状进行求解。层间总水头的求解，可以根据层间的渗透量相等的原则，所以，可以将图1的模型分为2部分，第1部分为水平面以下与围岩和注浆圈的交界面所组成的渗流区域，第2部分为围岩和注浆圈的交界面内所组成的渗流区域，如图3所示。

3 围岩渗流场

围岩中的渗流场可以通过模型的第1部分求解。图3(a)所示，此时渗流区域由地表边界、注浆圈边界与围岩组成，其可视为水下隧道洞周边等水头的稳定渗流问题，所以对围岩中的渗流场的求解方法与文献[10]中考虑洞周等水头条件下的渗流场的方法一致，可以采用文献[10]的方法根据其具体几何形状参数将其映射为矩形的像平面中，可得围岩内渗流场和渗流量Q。

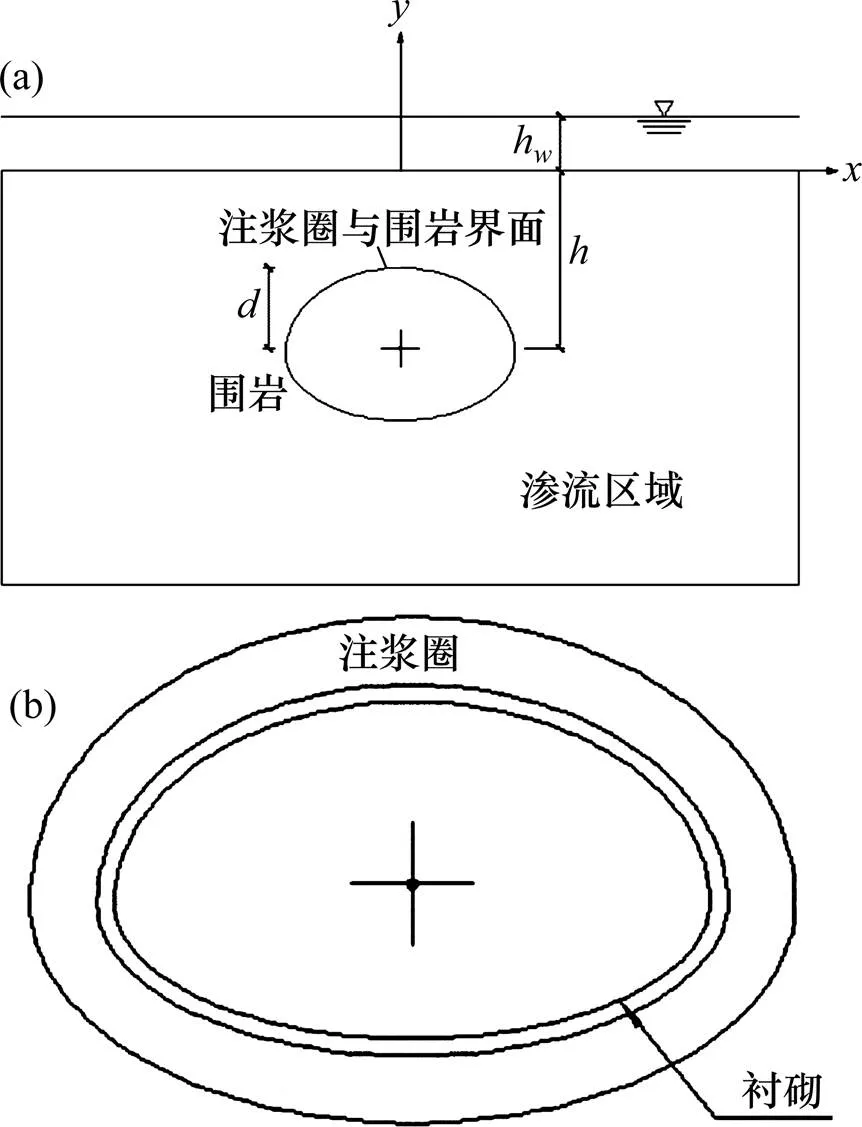
(a) 围岩渗流场；(b) 矩形映射

同样利用保角变换公式：

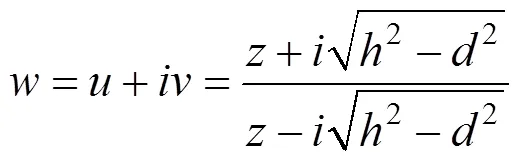
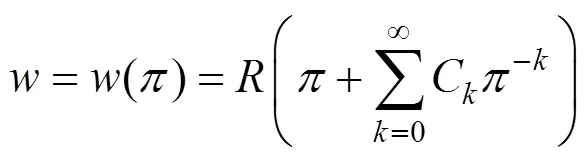
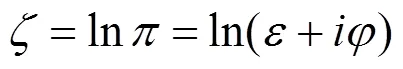
经过上式变换可将原来在围岩和注浆圈边界组成的渗流区域映射为矩形，其中矩形在方向上范围为0到r。在像平面中就可以很容易求得势函数的解φ和围岩内的渗流量Q：

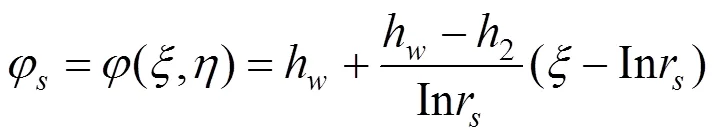
式中：r为其映射函数所确定的系数，h为围岩表面的压力水头，h为注浆圈与围岩界面的压力水头。

通过联立3个变换公式可以得到原平面和像平面中坐标点的对应关系的隐函数方程：

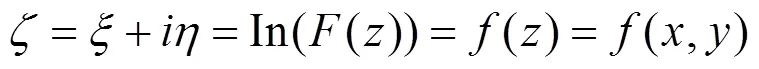
通过联立式(5)和(7)就可以求得返回原渗流平面，围岩中的渗流场：

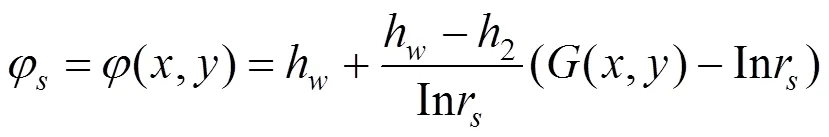
4 注浆圈渗流场

此外对于注浆圈内和衬砌内的渗流场可以通过模型的第2部分求解。由于注浆圈、衬砌形状与隧道形状一致，可以将其映射为一系列同心圆。为了便于计算，将原平面(平面)上的衬砌、注浆圈通过保角变换映射为像平面上的圆环结构形式。此时原平面上的区域3映射为像平面中的3；注浆圈区域2映射为像平面中的区域2；衬砌区域1映射为像平面中的1区域。同时其边界1，2和3分别对应映射为同心圆的1，2和3。

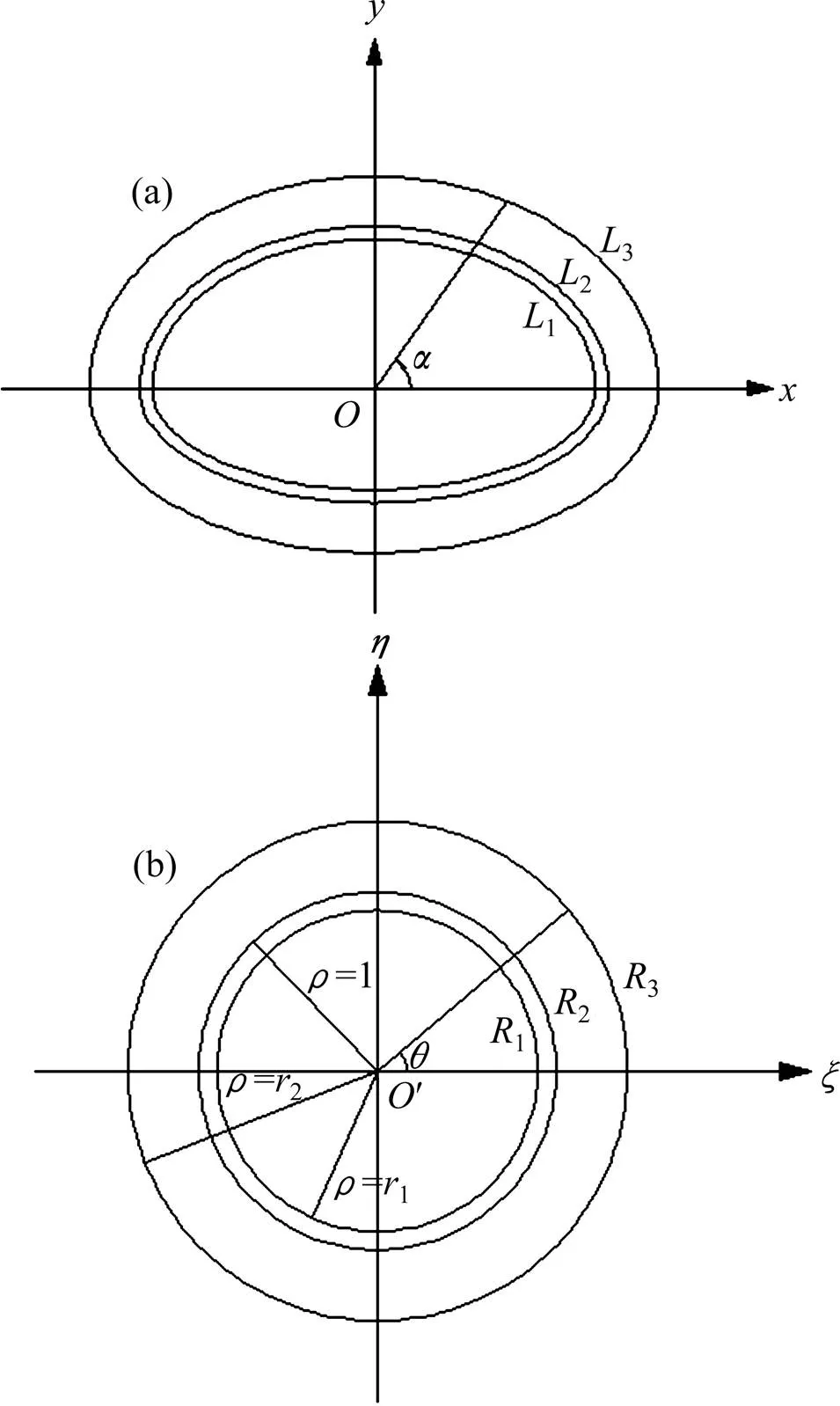
(a) Z平面；(b) ζ平面

此时映射函数的一般形式也可以用劳伦级数的表示[79]：

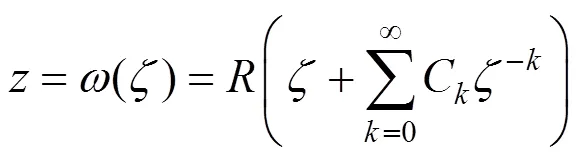
式中：为正实数，它反映隧道孔形的大小；C为复常数，其中=1, 2, 3,…，C反映了隧道横断面的形状，在多数情况下，级数中只需取很少几项就可以满足映射精度的工程要求，因为分析的是轴对称问题，C必为实数。再通过复合型最优化技术来确定此时的映射函数。为平面上的点映射为平面上的坐标点，可以用极坐标表示。

对于本章的问题，如图4，通过上述映射函数，将所对应的围岩与注浆圈的交界面3映射为半径=2的圆3，同时，将所对应的注浆圈与衬砌交界面映射为半径=1的圆，将所对应衬砌与大气交界面映射为=1的圆。

通过保角变换后，注浆圈在像平面中为圆环区域，可以在像平面中求解注浆圈内势函数的拉普拉斯方程(假设φ为注浆圈内任意一点压力水头，为极径)。

式(1)在像平面可以写成极坐标形式，在变换之后的圆域中，拉普拉斯方程可化为极坐标下的对称形式：

根据边界条件=2时φ=2；=1时φ=1；可以解得势函数φ，然后积分可得注浆圈渗流量Q。

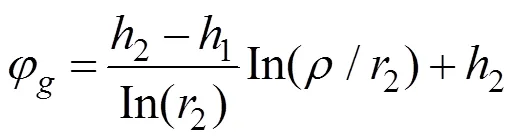
同理，衬砌内的渗流场计算，根据边界条件：=1时φ=0=0；=1时φ=1可得：

衬砌渗流量：

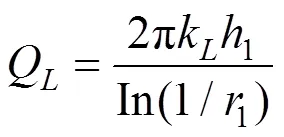
同样可以根据注浆圈内保角变换的变换函数式(9)可知道变换后注浆圈区域内点位与实际点位的关系，从而可以求出注浆圈中渗流场的解。

根据层间的渗透量相等Q=Q，Q=Q，可得：

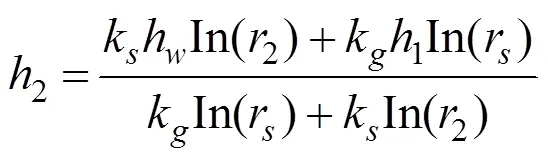
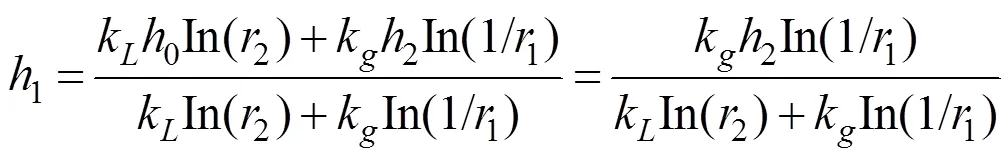
联立上面两式，就可以得：

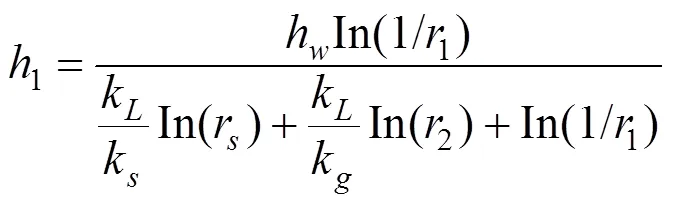
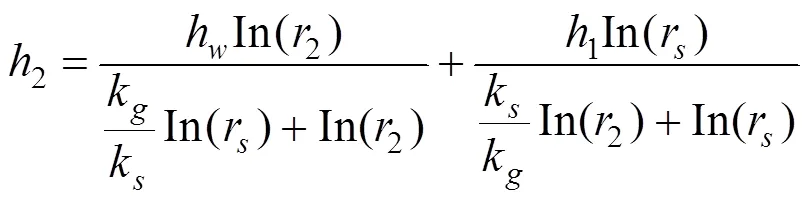
则隧道内的渗流量为：

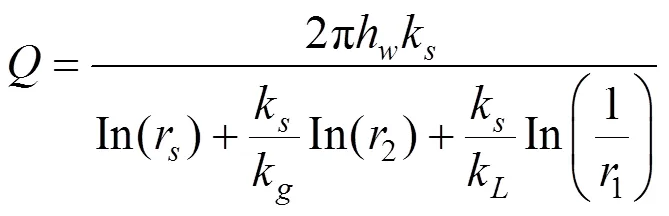
衬砌与注浆圈接触面的孔隙水压为：

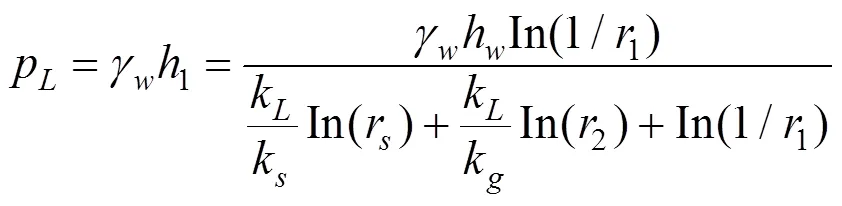
注浆圈和围岩接触面的水压力为：

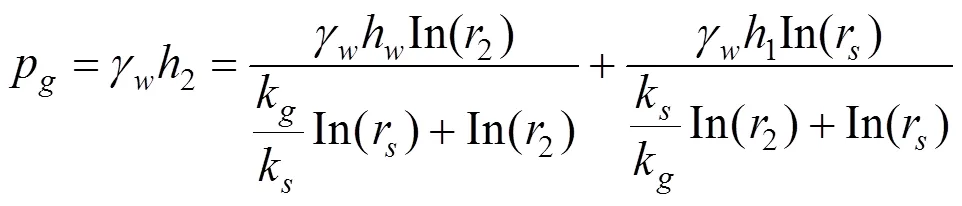
式中：r，1，2为特定图形经过保角变换所得变换函数的系数，当图形确定则系数就确定了，即可认为是任意图形的图形参数。

如果在隧道衬砌后设计排水系统，水只从排水系统排出时，即可以从已知的渗流量反推处衬砌之后的水头：

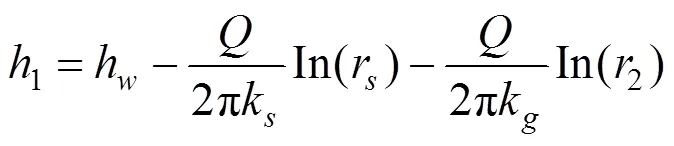
由式(21)可知，当排水量0时，衬砌后的水头为恒定值，与注浆和围岩渗透系数无关，即隧道采用全封堵模式，采用注浆方式不能分担衬砌上的外水压。

5 算例及验证

对于水下任意孔形隧道考虑注浆作用的渗流场的解也可以通过有限差分FLAC3D来验证其合理性。对于其形状特征，本节以水下椭圆形隧道为例，首先采用计算软件MATLAB编写特定孔形的变换公式，进而得到有关形状的参数，再进行本章解的计算，最后采用数值模拟软件建立数值模型并计算其数值解与本章解对比。

假设隧道为椭圆形，其几何模型参数：长轴和短轴分别为=8 m和=5 m，隧道内衬砌厚度为0.3 m，隧道中心埋深为=40 m，水位高于地表h=30 m，如果注浆的话，其注浆圈厚度均匀沿隧道中心增加。根据模型特性与其对称性建立图4~5所示的数值模型，为了消除边界条件影响，故在数值模型方面，取计算宽度共100 m，计算深度为160 m。数值验证选取的渗流参数：围岩渗透系数k=1.02× 10−11m2/Pa·sec(10−7m/s)，注浆圈渗透系数k= 1.02×10−12m2/Pa·sec，衬砌渗透系数k=1.02×10−11m2/Pa·sec，孔隙率为0.5，流体体积模量为=2 GPa，流体密度为=103kg/m3。同样因为是考虑稳定渗流，采用单相渗流模式，衬砌内壁设置等水头0=0的边界条件，地表边界根据水位的高度定义水头为30 m，通过设置不同渗透系数参数分别求解未注浆，注浆厚度=1, 2,…, 10 m情况下渗流场。

图5 椭圆隧道加注浆圈数值模型

根据隧道几何形状，求解此模型下注浆圈为1 m时的2种变换函数的系数。当注浆厚度为一米时，围岩和注浆圈外边界、地表边界形成的一个半无限平面中含埋深40 m、长轴为9 m、短轴为6 m的椭圆，根据[6]的方法求得其变换函数：

当=6时：r=10.615 4，

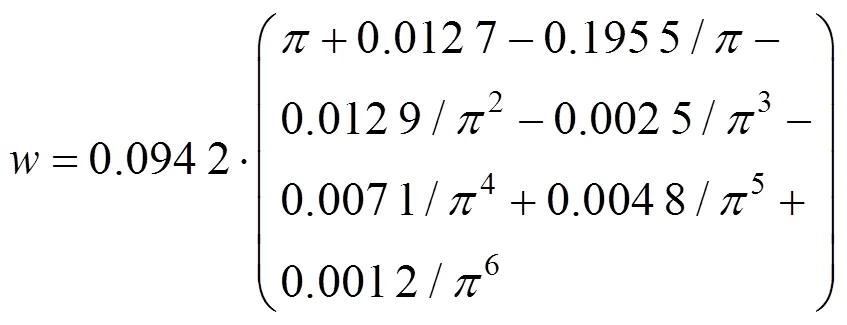
由注浆圈和衬砌所组成椭圆环通过式(9)映射成同心圆环，当衬砌厚度为0.3 m，注浆圈为1 m，其变换可以表示为：

当=6时：2=1.155 3，1=0.958 6，

上式：ζ=ρeiθ，当ρ=r2时，表示此映射函数映射成为注浆圈的外边界；当ρ=1时，表示此映射函数映射成为注浆圈的内边界；当ρ=r1时，表示此映射函数映射成为衬砌的内边界。由图6可以看出映射图形(红虚线)与实际图形比较，其误差非常小。

按照相同的方法，可以求出未注浆和注浆厚度=2,3,…,10 m时候的图形映射函数系数，其图形参数r，2和1随注浆圈厚度变化分别有表1给出。

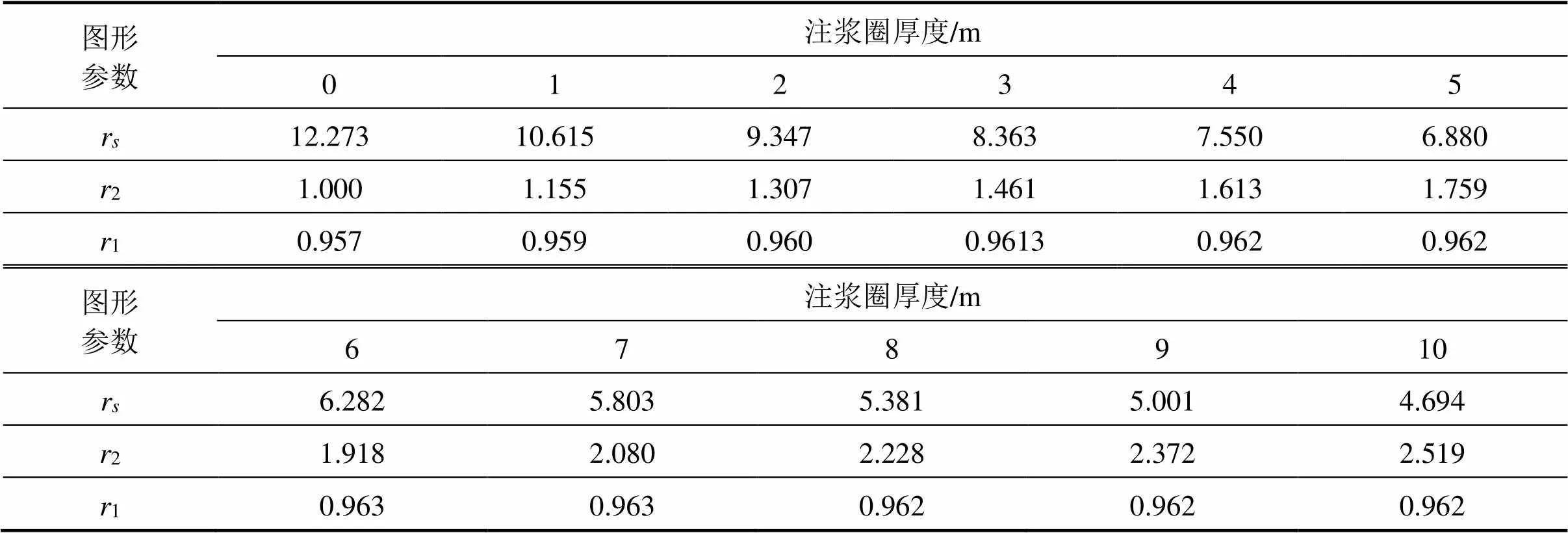
表1 不同注浆厚度下的图形参数

当具体形状的隧道的图形参数求得的话就可以通过本章所推导的公式求得隧道的渗流量，并与数值模拟FLAC3D解作比较，如图7。

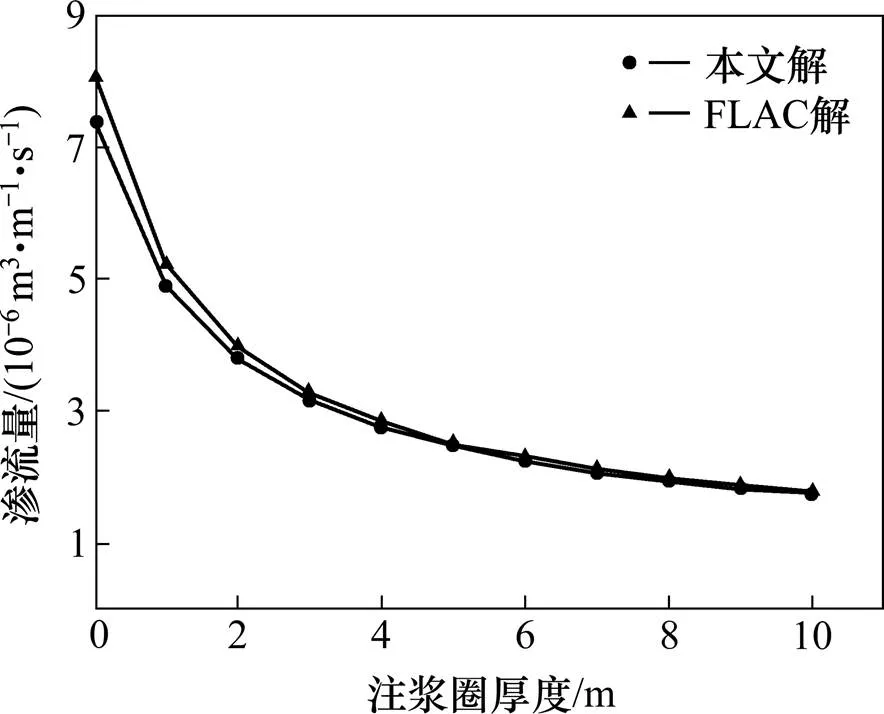
图7 渗流量与注浆圈厚度关系

由计算结果可知，本文解和数值解基本相等，最大误差发生在当未注浆时，本文求得此情况下隧道的渗流量为7.387 6×10−6m3/(m·s)，数值解结果为8.046 8×10−6m3/(m·s)，误差为8.19%。之后随着注浆后度增加，两种算法结果越为接近，但本文解整体偏小于数值解。由上图可知，通过注浆的方法明显可以减少水下隧道的渗流量，起到了非常好的堵水效果。有上述的解的结果可知，当注浆圈厚度为7 m时，隧道的渗流量相对于未注浆的时候降低了72.03%，随后随着注浆厚度的增加，渗流量的减小值明显下降，总值趋于不变，说明注浆达到一定厚度之后，再次增加其厚度对隧道堵水效果是不明显的，对工程来说是不经济的。

当注浆厚度增加对渗流量的影响不大时，可以考虑注浆材料对其堵水效果的影响。假设衬砌的渗透系数k和围岩的渗透系数k保持不变为10−7m/s，在上述注浆圈厚度为7 m的情况下，分别考虑围岩渗透系数与注浆圈渗透系数比值=k/k，为=10, 20, …, 100下的渗流量与渗透系数之间的关系，如图8所示。

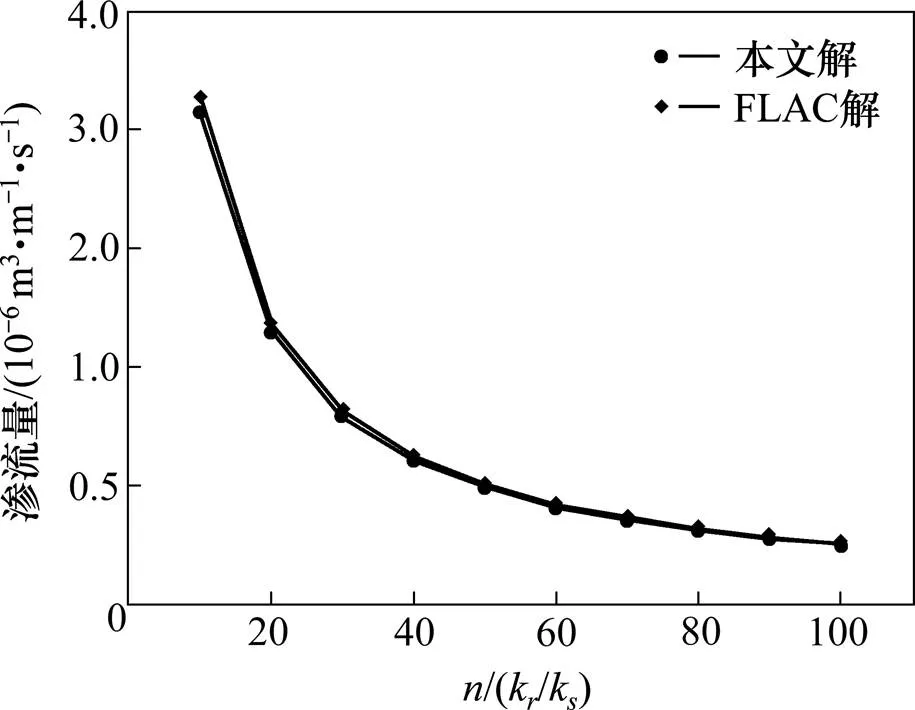
图8 渗流量与围岩注浆圈相对渗透系数的关系

由图8可知，在相同注浆量的情况下，隧道渗流量随着注浆圈渗透系数的减小而减小，当=50时的隧道渗流量(4.905 9×10−7m3/(m·s))只有=10时(2.066 5×10−6m3/(m·s))的23.74%，说明减小注浆圈的渗透系数也可以起到非常好堵水作用。但是随着其系数持续减小，渗流量减小速度也会变得缓慢，因此应对应实际工程设计时，应同时考虑注浆圈厚度与渗透系数大小。同时，通过本文解与数值解相比较，本文解整体小于数值解，但是平均误差仅为3.26%，两者几乎吻合，验证了本文解的正确与合理性。

6 结论

1) 基于文献[10]的基础上，再次利用保角变换，根据连续性原则，推导了毛洞在注浆圈和衬砌共同作用下水下任意形隧道渗流场的解。

2)以水下椭圆隧道为例分析了隧道渗流量与衬砌后水压力，并通过有限差分FLAC3D模拟了不同注浆圈厚度和渗透性情况下椭圆形隧道数值解与本例解相比较，证明了本文解答的正确性，为求解水下任意形隧道的稳定渗流场在考虑注浆情况下提供了一种快速、准确的方法。

3) 对于设注浆圈的水下任意孔形的隧道，只需了解隧道形状、埋深、和注浆厚度等设计尺寸，通过运用保角变换和最优化技术求得对应情况下隧道的图形参数，就可以求解该设计的隧道稳定渗流场，并给出其渗流量和衬砌外水压力的公式，且结果精确。

[1] El Tani M. Circular tunnel in a semi-infinite aquifer[J]. Tunnelling & Underground Space Technology, 2003, 18(1): 49−55.

[2] Kolymbas D, Wagner P. Groundwater ingress to tunnels- the exact analytical solution[J]. Tunnelling & Underground Space Technology, 2007, 22(1): 23−27.

[3] Park K H, Owatsiriwong A, Lee J G. Analytical solution for steady-state groundwater inflow into a drained circular tunnel in a semi-infinite aquifer: A revisit[J]. Tunnelling and Underground Space Technology, 2008, 23(2): 206−209.

[4] Harr M E. Groundwater and seepage[M]. New York: McGraw-Hill, 1962.

[5] 王秀英, 王梦恕, 张弥. 计算隧道排水量及衬砌外水压力的一种简化方法[J]. 北方交通大学学报, 2004, 28(1): 8−10. WANG Xiuying, WANG Mengshu, ZHANG Mi. A simple method to calculate tunnel discharge and external water pressure on lining[J]. Journal of Northern Jiaotong University, 2004, 28(1): 8−10.

[6] 杜朝伟, 王梦恕, 谭忠盛. 水下隧道渗流场解析解及其应用[J]. 岩石力学与工程学报, 2011(增2): 3567−3573. DU Chaowei, WANG Mengshu, TAN Zhongsheng. Analytic solution for seepage field of subsea tunnel and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2011(Suppl 2): 3567−3573.

[7] 童磊, 谢康和, 卢萌盟, 等. 半无限含水层中带衬砌隧洞渗流解析研究[J]. 岩土力学, 2011(1): 304−308. TONG Lei, XIE Kanghe, LU Mengmeng, et al. Analytical study of seepage flow into a lined tunnel in a semi-infinite aquifer[J]. Rock and Soil Mechanics, 2011(1): 304−308.

[8] 熊浩, 赵凯, 陈国兴. 海底隧道排水衬砌渗流场解析[J]. 地下空间与工程学报, 2015, 11(2): 499−504. XIONG Hao, ZHAO Kai, CHEN Guoxing Investigation on the analytical solution for the seepage field of subsea tunnels with partially water-proof-type lining[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(2): 499−504.

[9] 应宏伟, 朱成伟, 龚晓南. 考虑注浆圈作用水下隧道渗流场解析解[J]. 浙江大学学报(工学版), 2016, 50(6): 1018−1023. YING Hongwei, ZHU Chengwei, GONG Xiaonan. Analytical solution on seepage field of underwater tunnel considering grunting circle[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(6): 1018− 1023.

[10] 贺志军, 莫海强, 邹金锋, 等. 水下椭圆形隧道稳定渗流的近似解[J]. 铁道科学与工程学报, 2019, 16(9): 2265−2273. HE Zhijun, MO Haiqiang, ZOU Jinfeng, et al. Approximate analytical solutions for steady seepage into an underwater elliptical tunnel[J]. Journal of Railway Science and Engineering, 2019, 16(9): 2265−2273.

Study on seepage into arbitrary shape tunnel considering grouting ring

LI Jie1, MO Haiqiang2

(1. MCC (Guizhou) Construction Investment Development Co., Ltd, Guiyang 550009, China;2. School of Civil Engineering, Central South University, Changsha 410075, China)

The treatment method of “water blocking and limiting” is adopted in underwater tunnels at present. The water seepage volume of the tunnel and the water pressure of the lining are reduced by grouting and the drainage lining. In order to meet the needs of various engineering constructions, non-circular tunnels are very common in engineering practice. But at present, there are few studies on seepage into non-circular tunnels considering the case of grouting. In this paper, combined with the conformal mapping method, the solution of the seepage into the arbitrary-shape underwater tunnel with the grouting ring and the lining was presented. The comparison with FLAC3Dvalidates the proposed approach which provides a fast and accurate method for engineering requirements.

grouting ring; arbitrary shape; tunnel; seepage; conformal transformation