水中悬浮隧道受撞击作用的数值分析

陈灿鹏，孙文哲，王 琰，谭慧明

(1.中交第四航务工程勘察设计院有限公司，广州 510230；2.河海大学 港口海岸与近海工程学院，南京 210098)

水中悬浮隧道(submerged floating tunnel, 简称SFT)，是一种新的穿越水域的交通结构形式。它是根据阿基米德浮力定律，由结构在水中的浮力支撑隧道重量，并配备支撑系统以维持在水中的平衡和稳定。SFT通常有3种固定形式：(1)由立柱支撑；(2)由锚索锚固在水底，当隧道浮力足够大时，利用锚索拉力固定；(3)由水面浮箱承托，当隧道的浮力较小时增加浮力。与传统桥梁和隧道相比，其跨越能力大，布线灵活，全天候运营，建造成本相对较低，对环境影响小，是未来解决峡湾跨越、深海通道等重大交通工程的重要方式[1-2]。2018年，悬浮隧道工程技术研究列入中国科协发布我国面向未来60个重大科学问题和工程技术难题之一。

悬浮隧道在运营阶段除了波浪力、流以及隧道内车辆的移动荷载，还需考虑偶然状况下的地震、沉船潜艇撞击及爆炸等冲击荷载。尤其悬浮隧道处于深水环境，一旦发生结构破坏，将严重威胁人员安全及财产损失。对此有必要针对各种偶然状况下的结构受力和变形进行研究和模拟，以便提出抗冲击的设计方法和预防措施[2]。

项贻强[3]等将悬浮隧道简化为等间距弹性支撑梁, 基于Morison方程在考虑流体附加惯性效应和阻尼效应的基础上, 通过振型叠加法和Galerkin法得到振动微分控制方程, 并采用四阶龙格-库塔法进行数值求解，分析了移动荷载作用下悬浮隧道的动力响应。Tariverdilo[4]通过在二维和三维流场中对隧道附加质量积分的方法，来模拟流体的惯性效应，得到移动荷载下悬浮隧道的动态响应；麦继婷[5-6]等利用Morison方程和线性波浪理论, 计算分析了隧道放置深度、海流速度、流向与波向间的夹角、波浪周期等诸多因素对隧道所受水平波浪力的影响。Alberto[7]等人通过基于计算流体动力学(CFD)和有限元方法(FEM)，分别进行了动、静的流固耦合数值模拟，研究了变速水流中悬浮隧道的特性。

目前，针对悬浮隧道的研究[1-9]主要基于梁的弯曲振动模型，相关的理论分析及数值模拟也主要采用二维模型，计算模型的简化假定较多。同时，水体与结构相互作用是水下悬浮隧道撞击研究模拟的关键。本文采用流固耦合方法，建立水下浮筒式的悬浮隧道三维实体，分析不同撞击情况下水中悬浮隧道的受力和变形。

1 计算工况

图1 3种撞击位置的计算工况

本文模拟的浮筒式悬浮隧道，其主要结构包括水下的长隧道、上方水面处的浮筒以及连接浮筒与隧道的空心钢管桩。浮筒分别设置在隧道纵向长度左右四分之一跨处，并通过两根钢管桩与隧道连接。偶然状况下，船、潜艇等撞击物的撞击点具有随机性，对此分别选择3个特征撞击位置作为计算工况，包括隧道跨中、浮筒下方隧道处和浮筒中心处(图1)。

2 计算模型及参数

本文采用流固耦合方法，通过欧拉单元和拉格朗日单元分别模拟流体材料和结构材料，建立了悬浮隧道在水中受撞击作用的流固耦合模型。

2.1 几何及材料参数

图2 隧道断面图

悬浮隧道结构设计参数如表1所示，隧道断面如图2。隧道断面宽35.71 m，高11.4 m，隧道中心距水面25.7 m。浮筒半浮于水面，相邻两筒距离为200 m，连接管桩为空心钢管，半径为2 m。潜艇采用直径为12 m椭圆体进行简化，质量为10 000 t，水下初始速度为5 m/s。本文主要关注悬浮隧道的变形及受力，故隧道采用三维的线弹性实体单元，连接管桩为三维的线弹性梁单元，浮筒与撞击潜艇均设置为三维的刚体。

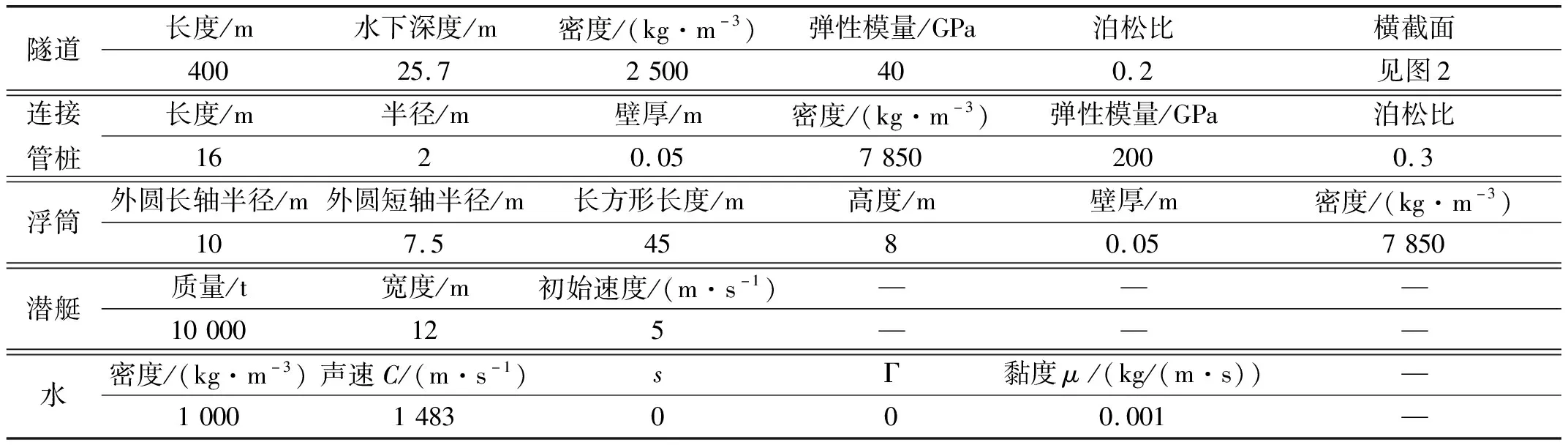
表1 模型几何及材料参数

2.2 初始水域

水域范围采用欧拉体。在欧拉网格中，材料在固定的网格内流动，欧拉体应包括水体在计算中所有可能流过的区域，故欧拉体尺度可为纵向长400 m，宽度100 m，高度60.7 m。由于水下隧道等拉格朗日体装配在欧拉体中，欧拉网格区域内初始水域分布情况应考虑结构的拉格朗日体所在区域。如图3所示，当潜艇在水下运动并撞击结构，欧拉体内水流与结构相互作用，结构变形，引起水体在欧拉体内流动，可见水面发生明显变化。

2.3 边界条件及接触

图3 撞击过程中水域表面变化

隧道两端约束3个方向位移；欧拉体侧面及底部约束法向速度；撞击潜艇预定义初始速度为5 m/s，方向为垂直指向隧道侧面。

流体与结构之间的相互作用采用动力分析模块的接触方法。

连接钢管与浮筒、连接钢管与隧道的连接通过钢管端点分别与相应面耦合连接。

全局施加重力加速度9.8 m·s-2。

3 数值模拟结果分析

3.1 撞击隧道跨中

图4 撞击跨中时变形云图(变形效果放大100倍)

图4、图5和图6分别为隧道整体变形云图、撞击力历时曲线和隧道纵向长度上的特征点位移曲线，可反映撞击过程中隧道变形情况和撞击物对隧道的作用力。当潜艇贴着隧道跨中表面以5 m/s的速度撞击，隧道受潜艇的撞击力迅速增加，跨中率先发生变形，而后向两侧影响，隧道整体成弓形，如图4所示。由图5可知，当时T=0.05 s，撞击力达到最大值N=1 276.02×103kN，而后迅速减小，潜艇与隧道分离，撞击力为零。由于惯性，隧道仍持续变形，当T=0.325 s时，跨中变形达到最大值d=0.181 6 m，而后向另一侧回摆。四分之一跨由于离撞击处稍远，同时上部浮筒及连接钢管约束，变形幅度小于跨中；隧道整体变形在中轴线两侧来回变化，变形幅值逐渐衰减。

图5 撞击力历时曲线

图7～9为隧道各结构内力和能量变化图。浮筒通过连接钢管桩对隧道变形产生作用，如图7拉杆力变化曲线所示，钢管桩主要承受拉力，由于隧道持续变形，隧道、浮筒、钢管桩与流体的相互作用，钢管桩内力呈现持续的起伏波动，最大值为F=80.50×103kN，后期变形中拉杆力趋于稳定维持在F=15×103kN左右。同时，隧道两端的水平横向约束力撞击初期变化剧烈，后期随整体变形来回波动，最大值为F=475.39×103kN，如图8隧道端部约束力曲线所示。由图9隧道动能变化可知，隧道的动能在撞击后迅速增加，最大值为35.14×103kJ，后呈波动的增减变化，最大幅值不断减小，总体为能量衰减的趋势。

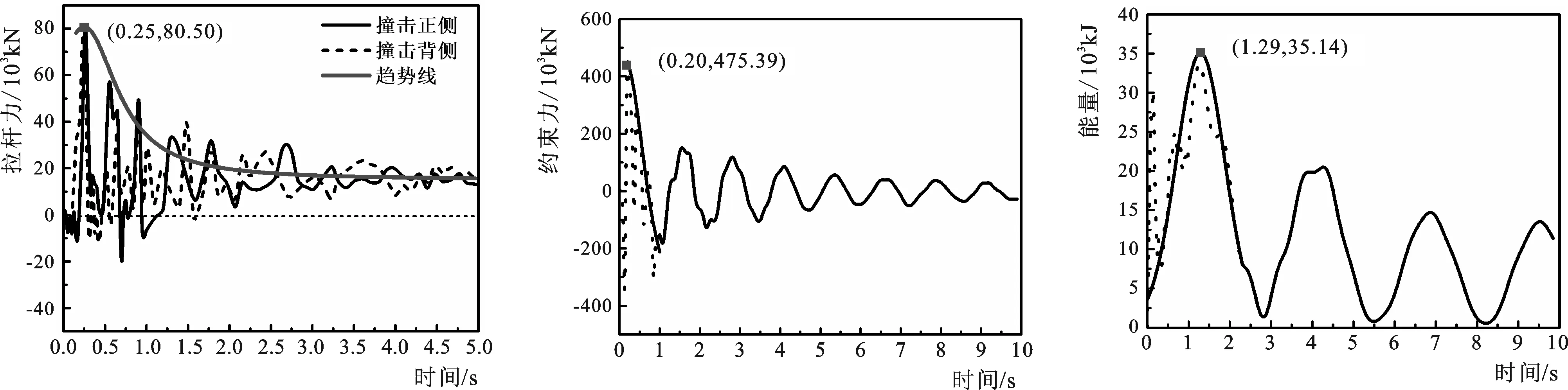
图7 拉杆力历时曲线

Fig.7 Duration curve tension rod force

图8 隧道两侧水平约束力历时曲线

Fig.8 Duration curve of horizontal restraint force

图9 隧道动能历时曲线

Fig.9 Duration curve of tunnel kinetic energy

3.2 撞击隧道四分之一跨

隧道整体变形云图、撞击力历时曲线和隧道纵向长度上的特征点位移曲线的变化规律，撞击隧道四分之一跨与撞击跨中相近(图10)。当潜艇贴着隧道左侧四分之一跨处表面以5 m/s的速度撞击，隧道受潜艇的撞击力迅速增加，在T=0.05 s时达到最大撞击力N=1 263.02×103kN。撞击处先发生变形，而后变形向远端传播，其相位领先跨中和远侧四分之一跨，最大变形位移值相近，最大值为d=0.110 m。达到最大位移值后，变形规律与工况一类似，会向初始位置处摆动，两侧四分之一跨处回摆幅度小于跨中；后期整体变形逐渐规律，变形幅值逐渐衰减。

隧道各结构内力图和能量变化图的变化规律，撞击隧道四分之一跨时与撞击跨中相近。钢管桩主要承受拉力，钢管桩最大拉力F=124.54×103kN，后期变形幅值减小后，逐渐趋于稳定值。靠近撞击侧的隧道水平横向约束力随整体波动变形受力方向来回变化，最大值F=830.21×103kN，在后期变形减小后，两端水平约束力也趋于零。隧道动能变化趋势与撞击跨中情况一致，最大值30.39×103kJ，近似正弦波动，总体能量衰减。

图10 撞击四分之一跨时变形云图(变形效果放大100倍)

Fig.10 Deformation when hitting the one-quarter span(100 times magnified)

图11 撞击浮筒时变形云图(变形效果放大100倍)

Fig.11 Deformation when hitting the float(100 times magnified)

3.3 撞击浮筒

图12 撞击力历时曲线

图11变形云图及图12撞击力曲线图中，当潜艇贴着一侧浮筒中心的表面以5 m/s的速度撞击，撞击力不断增加，其增加速度和最值小于工况一、二。由于浮筒在水面处无固定约束，撞击过程中不断偏移、位置调整，撞击力急剧变化。当T=0.17 s时达到最大撞击力N=630.59×103kN。撞击后，浮筒先发生向一侧的水平移动，撞击侧翘起。相连接的隧道也随之移动并有一定的扭转。越靠近撞击侧越先达到位移最值，3个特征位置处最大位移相近，最大值为d=0.097 m。

图13拉杆力曲线图所示，由于撞击一端翘起，撞击正侧钢管桩受拉力，撞击背侧受压力，最大拉力为119.05×103kN，最大压力为N=127.95×103kN。远侧浮筒相连的钢管桩，受扭转变形影响小，主要承受拉力，最大值F=124.62×103kN。当后期变形减小时，拉杆力均趋于稳定值，为隧道提供足够浮力。隧道端部约束力曲线和隧道动能变化趋势的变化规律与前两种工况相近，隧道两端水平约束力受隧道整体变形影响，最大值F=320.83×103kN，当后期变形约束力将趋近于零。隧道动能最大值30.13×103kJ。

综上，各撞击工况下的最值对比如表2所示。

表2 不同工况下变形及内力最值

4 结论

本文针对浮筒式悬浮隧道水下撞击问题进行了有限元数值模拟，通过对结构变形及内力分析，得到以下主要结论：

(1)潜艇撞击隧道中，撞击力迅速增加，达到最大值后不断减小，当潜艇脱离隧道后，撞击力为零。撞击跨中、撞击隧道四分之一跨两种工况下撞击力相近最大值为1 276.02×103kN。撞击浮筒处，撞击力增加频率和最大值均小于前两工况，最大值为630.59×103kN，由于浮筒无足够支撑，撞击力随浮筒位置发生急剧变化。

(2)撞击过程中，受撞击位置处先发生明显变形，而后向隧道两侧影响，隧道整体变形成波动形态。撞击跨中、撞击隧道四分之一跨、撞击浮筒3种工况中，最大水平位移分别为0.181 6 m、0.110 m、0.097 m，撞击浮筒工况下隧道会产生一定的扭转变形。后期变形成规律性的波动，幅值逐渐减小。

(3)连接钢管桩主要承受拉力，当撞击浮筒时因浮筒翘起，撞击侧一边承受拉力，一边承受压力。撞击跨中、撞击隧道四分之一跨、撞击浮筒3种工况中，钢管桩最大内力分别为80.50×103kN、124.54×103kN、127.95×103kN。后期隧道变形幅值逐渐减小，拉杆力也趋于稳定，以提供隧道足够浮力。

(4)由于隧道整体变形不断波动，隧道两端水平约束力方向也不断变化。撞击跨中、撞击隧道四分之一跨、撞击浮筒3种工况中，最大约束力分别为475.39×103kN、830.21×103kN、320.83×103kN。当隧道变形衰减，两端水平约束力也趋于零。

(5)撞击初隧道动能迅速增加，由于隧道不同能量之间转化，隧道动能成正弦波动，总体成衰减的变化趋势。3种工况中，隧道动能最大值相近，均为30×103kJ左右。

5 建议

由于悬浮隧道尚处于概念设计阶段，本文仅对其单一管节的部分特征位置进行撞击模拟，以下就本文仿真结果对悬浮隧道防撞设计提出建议：

(1)悬浮隧道的抗撞击设计应考虑可能的撞击位置，如撞击隧道跨中、隧道四分之一跨和水面浮筒等特征位置处。针对撞击过程的撞击力和变形值对隧道结构强度及尺寸进行合理抗撞击设计。

(2)隧道管节之间及隧道两端与陆基的柔性或刚性连接对于隧道撞击后的应力及变形过程影响很大，而柔性连接的短管节能够较好的通过管节自身的变位来充分缓冲撞击能量，但该连接方式需要结合正常使用过程的稳定性要求进行综合考虑。

(3)潜艇或船舶对隧道的局部撞击力极大，常规预应力钢筋混凝土隧道管节外壁无法承受，撞击处材料可能会迅速屈服并破坏，影响结构安全。建议参考码头结构的护舷防护方法，将局部撞击能量通过橡胶材料防护结构分散至结构各处。此外，在隧道断面设计中建议充分考虑外层混凝土破碎失效后的止水带承载下防水问题。

(4)浮筒和隧道之间的连接钢管在撞击下有可能在端部发生局部屈曲，影响连接件的使用安全。应考虑连接管桩的内力值大小及受力方向变化，选用管桩材料强度和尺寸参数。建议采用柔性钢缆等材料。