“0+1”和“1+0”一样吗
2020-06-08郜舒竹
□郜舒竹
“0+1”和“1+0”是否一样的问题,似乎过于简单,不是一个值得思考和回答的问题。无非是在算式中,“0”和“1”两个数字的摆放顺序不同,但计算结果都是1,是加法交换律的一个特例。如果进一步想,“0+1”和“1+0”都是符号组成的算式,凡符号都会指称或表示对象,对象可能是静态的事物,也可能是动态的过程或动作。那么“0+1”和“1+0”分别表示或指称什么?存在哪些差异?这样的问题,似乎就不太容易说清楚了。
一个加法算式“A+B”,其中出现了“A”“B”以及“+”三个符号,A和B表示数,+表示“运算(Operation)”。那么,究竟应当如何认识数(以下所说的数均限定为“自然数”)和运算呢?
一、自然数并不“自然”
什么是“数”?提及“数”,头脑中的“意象(Image)”是什么呢?可能是类似于“3”的符号,但“3”不是数,是表达数的一个符号。这样的符号或文字还可能是“三,叁,Three”等。因此“数”这个概念是不同于水杯、白马这些具体概念的,是抽象的。从古至今,许多前人大师都对数的抽象性有过论述。
19世纪德国数学家利奥波德·克罗内克(Leopold Kronecker,1823—1891)有一句广为流传的名言:“整数(自然数)是上帝创造的,其他都是人造的。”[1]之所以把数视为“上帝”创造的,就是因为在现实世界中,人感知不到数的存在。
20 世纪英国哲学家、数学家伯特兰·阿瑟·威廉·罗素(Bertrand Arthur William Russell,1872—1970)将人的认知对象分为两类,一类是像水杯、白马那样特殊的、具体的,称之为“殊相(Particulars)”。另一类是感觉器官感知不到的对象,诸如“数、空间、时间、关系”等,具有抽象性和普遍性,也叫“共相(Universals)”[2]。
凡此都是“二元(Dichotomy)”的“本体论(Ontology)”哲学观,认为认知对象分别“存在(Existence)”于两个世界:一个是感官可以感知的物质世界(殊相),另一个是人感知不到的精神世界(共相)。认知对象分为两类,一类存在于物质世界,另一类存在于精神世界,数就被认为存在于精神世界中。
鉴于数的抽象性特征,如果把“算”看作是以数为对象的“操作(Operation)”,自然也具有了难以理解的特征。对于类似“2+3”这样的算式,同样具有了抽象性,究竟应当如何认识这样抽象的对象?
二、涉身认知
20 世纪80 年代后,美国的乔治·莱考夫(George Lakoff)和马克·约翰逊(Mark Johnson)提出涉身认知的理论,否认精神世界的存在,认为人的认知是“涉身(Embodiment)”的,也就是与人的身体以及身体的活动联系在一起。这一理论缘于认知科学的三点发现[3]。
●人“头脑(Mind)”中的智力活动是“涉身的(Embodied)”,而不仅仅是头脑中的智力。
●人的思想往往是“无意识(Unconscious)”的。
●抽象概念的认识是依赖“隐喻(Metaphor)”的。
意思是,所有认知都是基于头脑、身体与环境的互动,做即是知,知即是做,在此过程中会无意识地形成思维方式,也叫“意象图式(Image Schema)”。这样的思维方式又会自然而然地、不自觉地应用到人的其他活动中。
对于抽象的对象,需要用具体的涉身活动进行隐喻或“类比(Analogy)”。莱考夫和拉斐尔(Nunez Rafael)于2000 年合作出版了一本名为《数学来自哪里:涉身头脑如何生成数学》的著作[4],其中关于数学涉身认知的基本逻辑可以概括为如下三点。
●数学本质上说是关于人的“思想(Idea)”的,而不仅仅是形式化的定义、定理、计算、证明、解题等。
●这样的思想源于人与环境的涉身活动和经验,而不是先验的。
●数学的认知应当通过涉身活动的隐喻得以实现。[5]
不妨用一个直观的示意图表示涉身认知的过程(如图1)。

图1 涉身认知示意图
图中表现出丰富的、反复的涉身活动,能够使人形成相对稳定的思维方式(意象图式),这样的意象图式映射(隐喻)到抽象概念,进而使得抽象概念有“意义生成(Sense Making)”。
从涉身认知的视角看,运算实质是“过程(Process)”以及过程中人身体的“动作(Act)”。从这个意义上说,“A+B”和“B+A”是两个不同的过程,其中数字符号“A”和“B”在算式中位置的交换,并不是“交换”的全部意义。了解二者作为过程和活动的诸多差异,才能凸显交换律的发生以及存在价值。
交换律实质是关于两个不同算式,其结果相同的判断。所谓判断,指的是肯定或否定的陈述,这样的陈述可能是文字语言,也可能是符号语言。所有这样的陈述,都需要辨别和证明是否为“真(Truth)”,辨别与证明的过程其实就是“推理(Reasoning)”的过程,也就是要回答“为什么”和“怎么知道”的问题。
人人都会承认“太阳每天升起”这个判断为真,人是怎么获得这个判断的呢?怎么知道明天太阳是否会升起呢?事实上,明天太阳是否会升起,是一个未来的、尚未发生的事情,那么此时此刻对人来说,就是未知的。人能够做出肯定的判断“明天太阳一定升起”,是依据过去“无一例外地太阳每天升起”的事实,这样的事实使人产生了“无一例外都如此”的经验。
数学课程内容中也有类似的判断,比如:平面上两点之间直线段最短,怎样知道这个判断是对的呢?因为古今中外没有发现例外,人的直觉经验就是如此。人无法找到除此之外的“更短”,而且这样的事实为所有人所公认。像这种源于经验的判断在科学史中叫作“经验的(Experiential)”[6],在数学中也叫作“公理(Axiom)”或“公设(Postulate)”,具有假设正确,无须证明的意义。
加法交换律作为数学中的判断,也具有经验的特点。是人从经验中归纳出来的规律,是运动与变化中的不变,这或许也是称之为“律”的原因,就像牛顿从物体运动的经验中归纳出物体运动的规律,后人称之为“牛顿三定律”,也属于经验的判断。接下来的问题是,“加”与人什么样的涉身活动有关?其中“交换”是如何体现的?
三、“加”与“交换”的涉身动作
“加(Addition)”作为运算,从认知的视角看,其涉身过程和动作很多。比如,利用容器的思维方式,把“加”视为向容器中“放入”的动作,反过来“减”就是从容器中“取出”的动作,两者是“互逆(Inverse)”的关系。
对于抽象的算式“1+2”,就可以用“向盘子中放入苹果”的动作进行隐喻。把一个盘子看作“容器”,如果规定运算顺序为从左向右,其中已经有1 个苹果,人“手持”2 个苹果“放入”这个盘子,结果盘子中有3个苹果,如图2所示。

图2 “1+2”示意图
其中的“手持”和“放入”就是涉身的动作。这个过程是否有意义,取决于三个要素:容器中的“原有”,放入过程中的“手持”,放入后的“结果”。图2中的“原有”是1个苹果,“手持”是2个苹果,“结果”是从1个苹果改变为3个苹果。
“2+1”与“1+2”的过程有所不同,容器中的“原有”是2个苹果,“手持”是1 个苹果,放入后的结果与“1+2”的结果相同,也是3 个苹果,如图3所示。

图3 “2+1”示意图
如果把盘中“原有”的苹果数用字母A表示,放入过程中“手持”的苹果数用字母B表示,那么“A+B”和“B+A”两个放入过程中,A 和B的角色是不同的,而且是将A 用B 替换,将B 用A 替换,也就是将A 和B 做了交换。千百年来不断重复出现的事实让人们获得了这样的经验:将“原有”的对象与“手持”的对象进行交换,会无一例外地使得放入的结果不变。
如果把“盘”和“手”视为两个不同的空间位置,那么盘中“原有”与“手持”对象的交换实质是不同空间位置对象的交换,此时反映出的规律是,对象空间位置的交换具有总量的“不变性(Certainty)”。
除此之外,交换律还可以体现在观察方向的变化上。比如,面对地面上的鸡(如图4)。

图4 “左3、右2”示意图
观察者的涉身活动是眼球的转动方向。如果“从左向右”看,先看见3 只鸡,后看见2 只鸡,由此隐喻算式“3+2”。如果“从右向左”看,先看见2 只鸡,再看见3只鸡,此时隐喻的算式就是“2+3”。无论怎样看,无一例外地发现共有“5”只鸡这个结果不变。因此观察方向“从左向右”和“从右向左”的交换,也具有总量不变的规律,因此交换律体现了人涉身活动方式的交换,不会改变总量的规律。观察方向的交换使得结果不变,实质是“对称(Symmetry)”的表现形式。比如:
●回文数:20200202
●回文句:上海自来水来自海上
●英文单词:level
●交换律:A+B=B+A
其特点都是观察方向“从左向右”与“从右向左”交换后,观察结果形式上都是一样的,所以交换律也叫作“对称律”。
综上,“加”作为运算的交换性,可以体现在空间位置和观察方向上。不仅如此,观察的时间顺序,“先”和“后”也是可以交换的。“先看到”和“后看到”,虽然时间顺序不同,但结果相同。图4中,“先左,后右”和“先右,后左”的观察,不仅有方向的差异,还有时间顺序的差异,但结果都是相同的。因此,交换同时具有时间、空间和身体动作的意义,空间位置的改变、涉身动作的改变、时间顺序的改变,都会使得形式或数量保持不变。
以上对于“加”以及“交换”的认识,是以手的动作和眼球的动作为主的涉身活动,还可以通过人“脚”的“行走”动作隐喻加法交换律。行走可以说是人最常见的涉身动作,可以看作意象图式,其三要素分别为“起点、路径、终点”。从时间顺序来说,“先走2 步,停止,再走3 步”和“先走3 步,停止,再走2步”,路径中的停止位置是不同的,但起点和终点是一样的,如图5所示。所以“先走”和“后走”,作为时间顺序是可以交换的。

图5 行走示意图
这样时间顺序可交换的经验是很普遍的。比如学生熟悉的上课顺序,第一节课是数学,第二节课是语文,因为特殊情况,可能改为第一节课是语文,第二节课是数学,总的上课门类不变。
综上,所谓交换律“A+B=B+A”,可以说是来源于人经验的判断,其正确性是经验归纳的结果。具体表现为空间位置的交换、观察方向的交换以及时间顺序的交换。
四、“0+1”与“1+0”的区别
回到文初关于“0+1”和“1+0”的问题。从容器隐喻看,“0+1”中的“0”可以表示一个空盘子,其中没有苹果。“+”表示“放入”动作,“1”表示“手持”以及放入的苹果数,那么“0+1”就表示“向空盘中放入1个苹果”,如图6所示。这是可以理解的过程和动作,“0+1”的过程和动作可以在头脑中出现“意境(Imagery)”,进而有意义生成。
按照同样的容器思维,“1+0”表示盘中原有1个苹果,“+0”表示放入“0”个苹果,也就是没有放入苹果,如图7所示。
此时“1+0”表示“向原有1 个苹果的盘子中没有放入苹果”,这样的过程就不符合人涉身活动的规律。“放入0 个”等同于没有放入,也就是放入的动作原本就没有发生,使得“1+0”这样的算式无法在头脑中出现合理的意象,因而从认知的角度说,“1+0”缺少实际的意义。
用行走隐喻看,“0+1”可以看作是站在“0 起点”,走了1步,如图8所示。
而“1+0”是站在“1”起点,走了“0”步,等同于原地不动,没有行走,如图9所示。这也同样不符合人的涉身活动规律。

图6 “0+1”示意图

图7 “1+0”示意图

图8 “0+1”行走示意图

图9 “1+0”行走示意图
因此从涉身认知看,“0+1”与“1+0”有本质的不同,前者可以与人的涉身活动直接建立联系,进而具有意义生成。而后者相对于前者,在容器和行走图式中,没有出现有意义的动作,因此具有抽象的特征。也就是说,作为加法交换律的特例,“1+0=0+1”,不具备经验性判断为真的特征,其正确性就成为一种“建构(Construction)”,或人为规定。区别于经验性的“规律(Law)”,可以称之为“规则(Rule)”。
由此带来两个问题,第一,数学中为什么需要像“1+0”这样无实际意义的内容?第二,应当如何认识这样抽象的内容?《义务教育数学课程标准(2011 年版)》第21 页课程内容板块“数的运算”第三款中指出:“探索并了解运算律(加法的交换律和结合律、乘法的交换律和结合律、乘法对加法的分配律)……”其中的“探索”,或许就是期望学生进行认知,不仅停留在“知道+应用”,还应当经历“发生+发展”的过程。
数学中承认“+0”的存在,把“0”视为一个数学中的对象,把“+0”视为一个真实存在的运算,究竟是为了什么?
五、“+0”的意义
数学家通常具有“结构(Structure)”的思维,把数学对象看作是相互关联的整体。全体自然数及其运算就构成一个结构,结构的表达需要统一的形式。如果用统一的形式表达交换律“A+B=B+A”,字母A和B可以表示任意自然数,也可以拓展到分数(有理数)、实数、复数。其中的字母A 或B 允许为“0”,能够使得统一的表达形式具有普遍意义,而且允许“+0”的存在,并不妨碍“A+B=B+A”的普遍性和正确性,也就是这样的规定具有无矛盾性。
另外,把“0”视为一个存在的思维对象,在计算与推理中,也是有用的,能够成为实现算式或代数式之间转换的桥梁。比如:
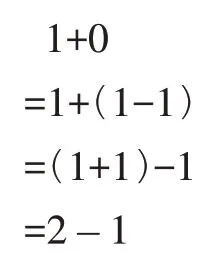
“2-1”和“1+0”是两个不同的运算,把“0”视为“1-1”,就把两个不同的算式联系到一起,可以相互转化。这样的思维方式实质是把“+0”看作“无中生有”的过程,把“无”视为“有”,创造条件,让“无”与“有”这样对立的双方,实现了相互转化。因此“+0”的过程,体现了对立统一的“辩证思维(Dialectical Thinking)”[7],而且对于算式转换具有实际意义。
比如,为了计算“19+21”,可以无中生有地添加“0”,算式变为“19+0+21”,由于0=1-1,因此变形为“(19+1)+(21-1)”,也就变成了“20+20”,使得通常所说的简便运算得以实现。简便运算的实质就是这样的算式转换。
再比如初中数学中解一元二次方程“x2-4x+3=0”,需要对左边代数式因式分解,通常采用所谓的“十字相乘法”,其实这一方法源于“+0”。

其中第二行,无中生有地添加了“0”,也就是添加了“1-1”,进而凑平方后,利用平方差公式实现了因式分解。
综上所述,“加”作为数学中的运算,其意义不仅是从算式到结果的“算(Calculation)”,背后是人的“运(Operation)”,也就是涉身的动作。所谓交换律,反映的是“空间位置、观察方向、时间顺序的交换,使得总量不变”的规律,是从多种多样、丰富多彩的动作经历中归纳出来的经验,是对运动与变化中不变因素的“归纳(Induction)”,是对经历中经验的“抽象(Abstraction)”。抽象出来的规律,在自然数集合结构中成为“法则(Rule)”,是计算过程中需要遵守的。
一个特例是对“1+0=0+1”的理解,从涉身动作的角度看,“0+1=1”具有实际意义,而“1+0=1”具有人为规定的特征,更一般的陈述是:任何数与零相加的结果还是这个数。这样的规定在符合无矛盾的前提下,能够保证自然数结构的“统一(Unity)”。同时,把“0”视为两个相同数相减的结果,在实际计算中实现算式间的转换,也是有意义的。
计算教学,往往追求“算”得“又对又快”,某种意义上忽略对算式的理解。这样容易导致的结果是:
●会做,但不懂。
●做对,但不会。
“算”成了依照程序的机械性操作,机械性操作成了“模仿+练习”的机械性训练,失去了理解的过程和多样的生成。因此应当倡导拓展对于计算教学的理解,不仅关注算式之后的结果,更应关注算式之前的发生。让学生有时间、有机会亲身经历算式发生与发展过程中的丰富多彩的涉身活动。真正实现“人人有活动、人人有机会、人人有发展”的理想教学。
