截球形雷达天线罩风荷载计算比较研究

孔德怡，祝时召

(1.海军东海工程设计院，上海 200434； 2. 91144部队，辽宁 大连 116044)

无论在军用还是民用领域，雷达作为观察预警、天气预报还有通信导航的应用都是越来越普遍。雷达天线作为装备的重要组成部分，一般需要布置在地势高、视野好的点位，通常位于高山海岛，对其威胁最大的因素之一就是强风[1]。为了保护天线不受恶劣外部环境的影响能够正常工作，现行的通用做法是在天线外部设置天线罩。常见的天线罩为截球形，直径从3～20 m不等。由于球面流体计算机理较为复杂，设计人员常常无法较为准确计算天线罩上的风荷载，导致在天线罩设计以及基础设计上存在隐患[2-3]。因此，研究天线罩风荷载计算方法十分有必要。覃海艺等[4]通过有限元法研究了风荷载作用下天线罩的稳定和强度问题，但是对于风荷载分布形式没有深入探讨；王紫等[5]提出了一种四偶极子模型，用于预测球罩风载体型系数；孙磊[6]、靖峰[7]等通过CFD方法模拟了天线罩风荷载，给出了风荷载分布规律。但是以上计算方法不便于一般设计人员掌握并加以应用。本文基于现行设计中主要采用的两种计算方法，比较了异同，分析了原因，给出了推荐的设计思路和方法。

1 荷载规范方法

根据《建筑结构荷载规范(GB50009—2012)》[8](以下简称《规范》)，垂直于围护结构表面上单位面积风荷载标准值，应按下列公式计算：

wk1=βgzμslμzw0

(1)

其中：βgz为高度z处的阵风系数；μz为风压高度变化系数；μsl为围护结构的风载体型系数；w0为基本风压。阵风系数和风压高度系数均可查表得到，基本风压与计算风速有关，而风载体型系数是计算的难点。规范中没有截球外形的风载体型系数计算公式，与之最相近的是旋转壳顶。根据规范表8.3.1第36款之规定，旋转壳顶体型系数公式为

μsl=0.5sin2φsinθ-cos2φ

(2)

其中：θ为平面角;φ为仰角，参见图1。从式(2)可知，μsl有正有负。其中正值表示压力，负值表示吸力。

图1 计算简图

把式(2)代入式(1)，则雷达天线罩表面任意点A(φ，θ)处单位面积的风荷载为

wk1(φ，θ)=βgzμzw0(0.5sin2φsinθ-cos2φ)

(3)

取A点为中心的微小面积dA，详见图2，其中dA=R2sinφdφdθ，其中R为天线罩大球半径。则垂直于该微小面积上的风荷载为：

dwk1=βgzμzw0(0.5sin2φsinθ-cos2φ)R2sinφdφdθ

(4)

为了便于设计使用，将垂直于天线罩的风荷载向三向直角坐标系投影，则：

Fx=∬βgzμzw0(0.5sin2φsinθ-cos2φ)R2sin2φsinθdφdθ=

2CD1βgzμzw0R2

(5)

Fz=∬βgzμzw0(0.5sin2φsinθ-cos2φ)R2sinφcosφdφdθ=

2CL1βgzμzw0R2

(6)

Mw=h0×Fx=2CM1βgzμzw0R3

(7)

其中:Fx即风荷载作用下，天线罩底部总的推力；Fz为总升力；Mw为总倾覆力矩；h0为天线罩大圆中心距离基础顶面的垂直距离。CD1为推力计算系数；CL1为升力计算系数；CM1为倾覆力矩计算系数。

实际运用式(5)～式(7)时，需要分区域计算。以上半球为例，在吸力区域，垂直表面的风荷载计算为负值，其带来的推力和升力分量都是对结构不利；而在压力区域，垂直表面的风荷载计算为正值，其推力分量对结构不利但是升力分量对结构有利。在积分计算时要尤其注意。计算得到的系数表达式如式(8)～式(10)。从公式中可以得知，各个系数均为φ0的函数，其中φ0为天线罩底部对应的仰角值。

CD1=0.25π(0.375φ0-0.1875sin2φ0-

0.25sin3φ0cosφ0)

(8)

CL1=-0.25π(cos4φ0-1)

(9)

CM1=CDcos(π-φ0)

(10)

2 拟合公式法

《建筑结构荷载规范》提出方法主要针对常见的建筑结构形式，式(2)是针对旋转壳顶提出的近似公式，与天线罩的截球外形还是有区别的，是否合适有待评价。而在文献[9]中提出了用以式(11)计算作用在罩体表面的风荷载wk2。

wk2=k3k4μs2w0

(11)

μs2=-1.3+0.180 1sinφcosθ+0.78sin2φ+

0.78sin2φcos2θ+0.14sin3φcos3θ+0.42sin3φcosθ

(12)

其中k3为超载系数，是为了考虑实际受风时有一定的安全储备，一般取1.2～1.3；k4为高度系数，与μz意义相同；μs2为球罩体型系数；θ为平面角，φ为仰角。

与《规范》式(1)对比发现，两者公式形式基本相同，主要的区别在于系数不同。相比于阵风系数βgz，超载系数k3取用较为主观，物理意义不明确，体现了落后的安全系数设计理念，与先进的可靠度设计理念不相容。且查《规范》表8.6.1可知，βgz不小于1.4，任何情况下均大于k3。

按照与规范方法同样的推导过程，得到基于拟合公式法的推力计算系数CD2、升力计算系数CL2和倾覆力矩计算系数CM2。同样，各个系数均为φ0的函数。

CD2=0.090 05π(-cosφ0+0.333cos3φ0+0.667)+

0.21π(-0.2sin4φ0cosφ0-0.8cosφ0+

0.267cos3φ0+0.533)

(13)

CL2=-0.65πsin2φ0+0.195πsin4φ0

(14)

CM2=CDcos(π-φ0)

(15)

将式(13)～式(15)代入式(5)～式(7)，并将βgz和μz替换成k3和k4，即可得基于拟合公式法的风荷载总推力、升力和倾覆力矩。限于篇幅不再列出。

3 对比分析

为了直观的比较两者风荷载计算的区别，将两种方法计算的罩体表面的风荷载按式(16)～式(19)转换为无量纲的平均风压系数CP、推力系数CPD、升力系数CPL和倾覆力矩系数CPM。地面粗糙度类别统一取B类，球罩顶距离地面高度10 m。根据《规范》，βgzl=1.7；μz=1.0。根据文献[5]，k3=1.2；k4=1.0。

CP=wki/w0(i=1,2)

(16)

CPD=Fx/(2w0R2)

(17)

CPL=Fz/(2w0R2)

(18)

CPM=Mw/(2w0R3)

(19)

首先比较不同仰角φ处的风载体型系数，如图2～图4所示。横坐标代表平面角θ值，根据对称性取一半(0°～180°)分析。其中球体赤道面迎风点位，θ=0°，φ=90°；赤道面背风点位，θ=180°，φ=90°；最高点位，φ=0°。

图2 规范公式不同仰角φ处的体型系数曲线

图3 拟合公式不同仰角φ处的体型系数曲线

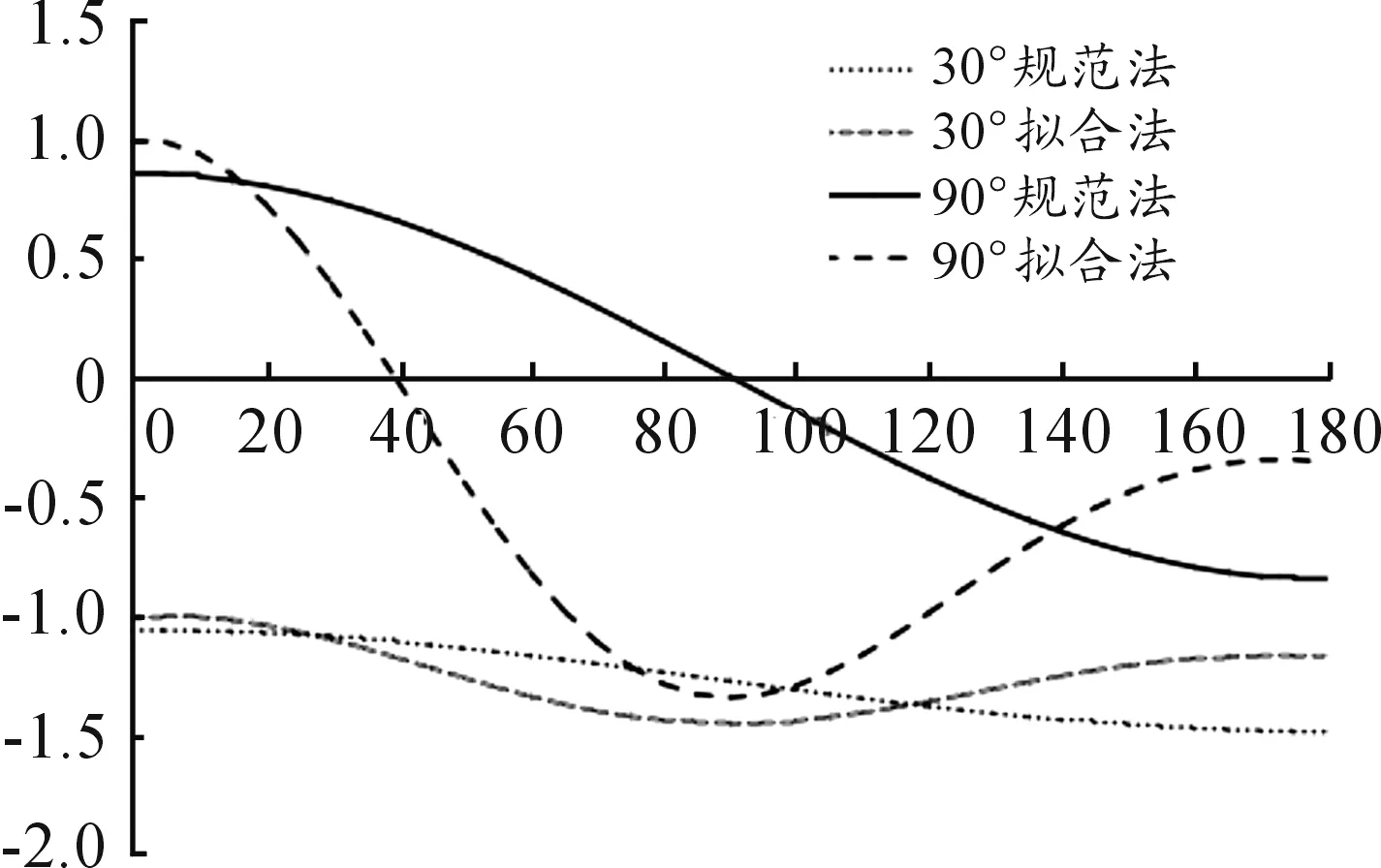
图4 两种方法不同仰角φ处的CP曲线

从图2、图3可以看出：无论是《规范》算法还是拟合公式，风吸力最大点均位于球罩顶点，风推力最大点均位于球罩赤道面的迎风点。这与直观感受和风洞实验数据吻合。比较图2、图3可以看出，两种方法对应位置处的体型系数值结果差别较大且变化规律并不完全一致。以天线罩赤道面为例，背风点位(最大吸力)《规范》方法风载体型系数为-1而拟合公式法为-1.3；迎风点位(最大压力)《规范》方法风载体型系数为0.5而拟合公式法为0.82。《规范》图形类似余弦函数而拟合公式法则不同。

图4进一步对平均风压CP进行了比较。发现在考虑了高度、阵风和超载等因素影响后，接近球罩顶点区域(φ=0°～30°)，两者差别较小；靠近正面迎风区域(θ=0°～20°)，两者差别数值接近；靠近截球侧面区域(θ=20°～140°)，两者差别较大且拟合公式法风吸力远远大于《规范》法；背风区域(θ=140°～180°)，拟合公式法风吸力小于《规范》法。

按式(17)～式(19)将两者计算得到的无量纲推力系数、升力系数和倾覆力矩系数绘图比较如图5～图7。

图5 CPD曲线

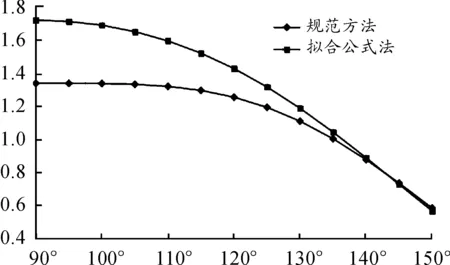
图6 CPL曲线

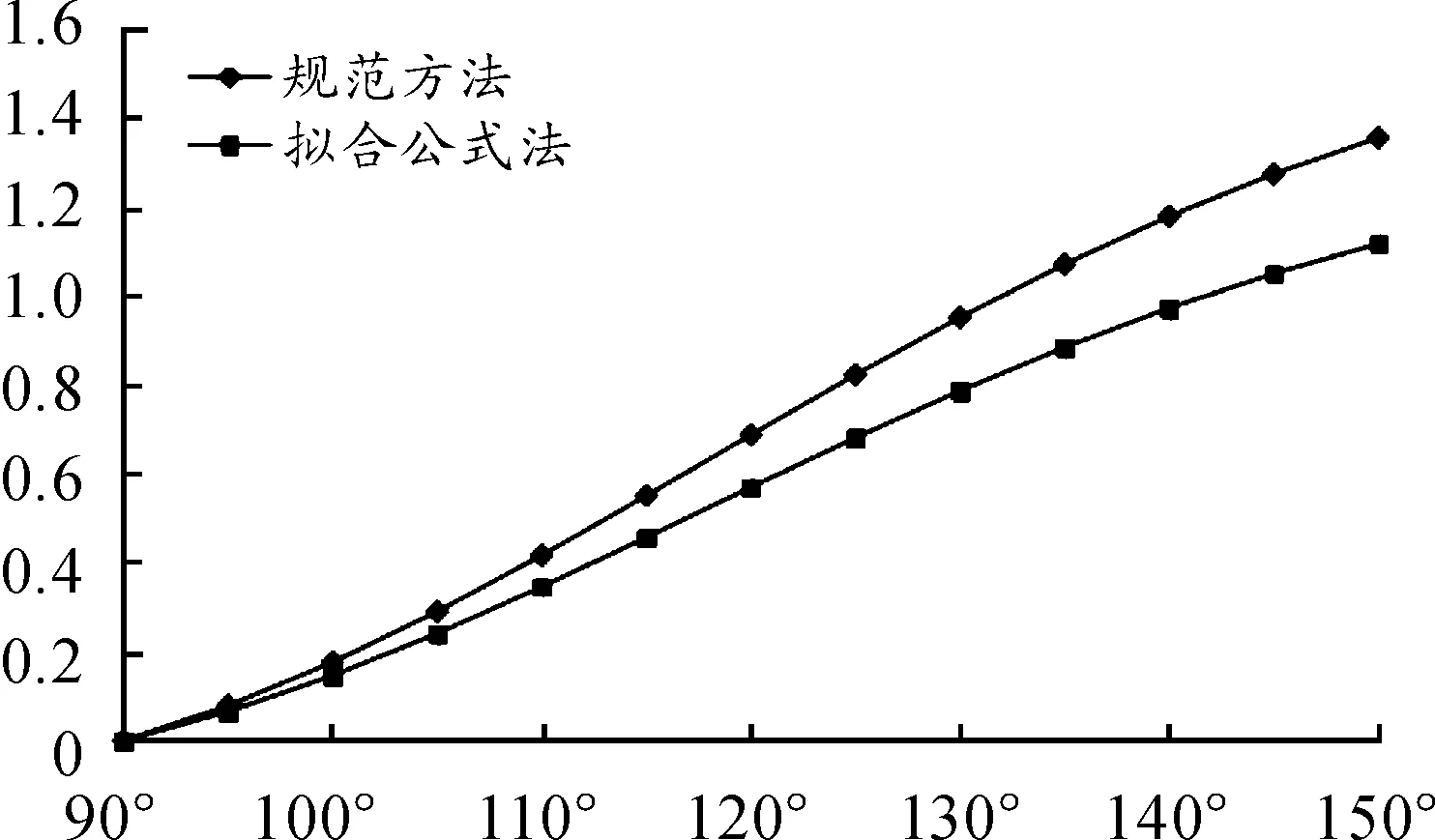
图7 CPM曲线

从图5～图7可以看出：两者计算系数变化规律基本相同，但是具体数值有不同程度的差异。总的来说，拟合公式推力和倾覆力矩系数小于基于《规范》计算得到系数，升力则是拟合公式法为大。结合图4可知，这是因为在球罩侧面区域(θ=20°～140°)，拟合公式平均风压远大于《规范》平均风压，这个区域的风压主要分量是升力，由此导致前者的升力较大。以常见的仰角φ0=120°截球天线罩为例，拟合公式法推力和倾覆力矩比规范值小17.1%，升力则大13.8%。

4 与风洞数据对比

从以上两种方法对比可以发现，风荷载计算结果差别较大。这给实际工程设计应用带来了困惑和不便。接下来分别按以上两种方法计算罩体表面平均风压分布，并与文献[10]某截球形雷达天线罩模型风洞实验数据对比，进一步评价两种方法的的适用性。限于篇幅，选取仰角30°、60°和90°三种典型截面风压分布绘图，如图8、图9和图10所示。

图8 仰角30°时的CP曲线

图9 仰角60°时的CP曲线

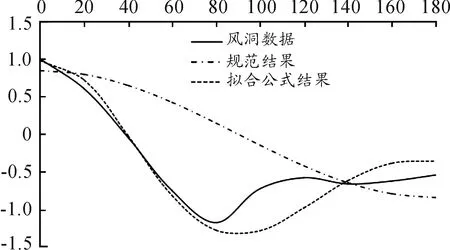
图10 仰角90°时的CP曲线

从图8～图10可以看出：拟合公式平均风压系数曲线与风洞实验数据吻合较好，而《规范》系数曲线则与实验数据差别较大。由此说明，《规范》给出的旋转壳顶风载体形系数并不完全适用于截球天线罩外形，而拟合公式给出的式(12)则能够较好的反应实际情况下天线罩的风荷载分布情况。结合图6可知，《规范》方法低估了风荷载对天线罩的升力作用，存在一定的安全隐患。这也与2006年桑美台风登陆时，浙南山区某雷达天线罩发生的从基础整体拔出事故相印证。

5 结论

《规范》给出的旋转壳顶风载体型系数并不完全适用于截球形天线罩。拟合公式给出的风载体型系数与风洞实验数据吻合较好，能够较为真实的反应风荷载在球罩表面的分布情况。对于风推力和倾覆力矩，拟合公式计算结果小于《规范》结果；对于风升力，拟合公式计算结果大于《规范》计算结果。拟合公式超载系数k3意义不明确，不能与现行的可靠度设计理论兼容。《规范》给出的阵风系数βgz物理意义明确，与整个结构设计规范体系相容，且大于k3。因此建议在天线罩及基础设计时，用式(12)计算风载体形系数代入式(1)，按规范方法计算球罩表面风荷载。如此既能保证风压分布贴近实际情况，又保证了风荷载作用下结构的可靠度，且未明显增加材料及建设成本。