精锻成形身管力学性能预测分析与工艺优化

2020-06-07毕梦凡樊黎霞扶云峰任青松张必良

兵器装备工程学报 2020年5期

毕梦凡，方峻，樊黎霞，扶云峰，任青松，张必良

(南京理工大学, 南京 210094)

精锻成形工艺是一种精确高效的身管制造工艺，能保证最高的成形与性能质量[1]。身管作为一种空心厚壁圆管，弹丸发射时膛内受到高温高压火药燃气的影响，工作环境恶劣，对其寿命等产生了极大的影响。试验证明，合理的身管锻造工艺可以有效地提高身管性能[2]。目前，在精锻成形工艺参数对身管锻后性能的影响方面已经作了大量的研究，包括线膛部分工艺参数对锻后性能影响[3]和弹膛部分工艺参数对锻后性能影响[4]，锻造比对膛线成形质量的影响[5]等。在分析锻后身管力学性能时，通过试验研究过程繁琐且周期较长，并且没有统一的评价方法。在国内，锻造工艺对身管锻后力学性能影响[6]方面的研究几乎为空白，尤其缺乏一种预测身管锻后力学性能的合适模型。合适的身管锻造工艺参数可以保证身管在成形后的力学性能要求。在身管设计尺寸和锻透性要求的前提下需要对身管进行试验分析，使其满足力学性能要求[7]。经大量试验研究，发现锻造比是影响身管线膛精锻力学性能的主要因素，精锻成形过程包括两个阶段，下沉段和锻造段，分别对应下沉段锻造比和锻造段锻造比[8]。为测试精锻成形身管力学性能，测定各项力学性能指标水平，本文对锻后身管进行拉伸与胀形试验，分别对应纵向性能和横向性能：纵向性能包括屈服强度、抗拉强度、断面收缩率、延伸率，横向性能包括屈服强度和延伸率[9]。为了使锻造试验数据更具有代表性，对过程参数基于软件Design-Expert试验设计，运用响应面模块分析锻造比参数与力学性能指标[10]，拟合精锻成形身管函数模型。综合步兵自动武器及弹药设计手册[11]与非标胀形试验的横向力学性能的重要性，确定身管锻后力学性能各指标设计规范。

1 基本理论与方法

精锻成形身管的力学性能预测、评估与优化包括各指标力学性能预测、身管力学性能合格性评估与锻造过程参数优化3部分。通过建立身管响应面曲面方程预测下沉段锻造比与锻造段锻造比对各指标力学性能的影响。利用响应面分析拟合试验数据，根据R2回归系数选择拟合精确的模型。分析与优化流程如图1所示。

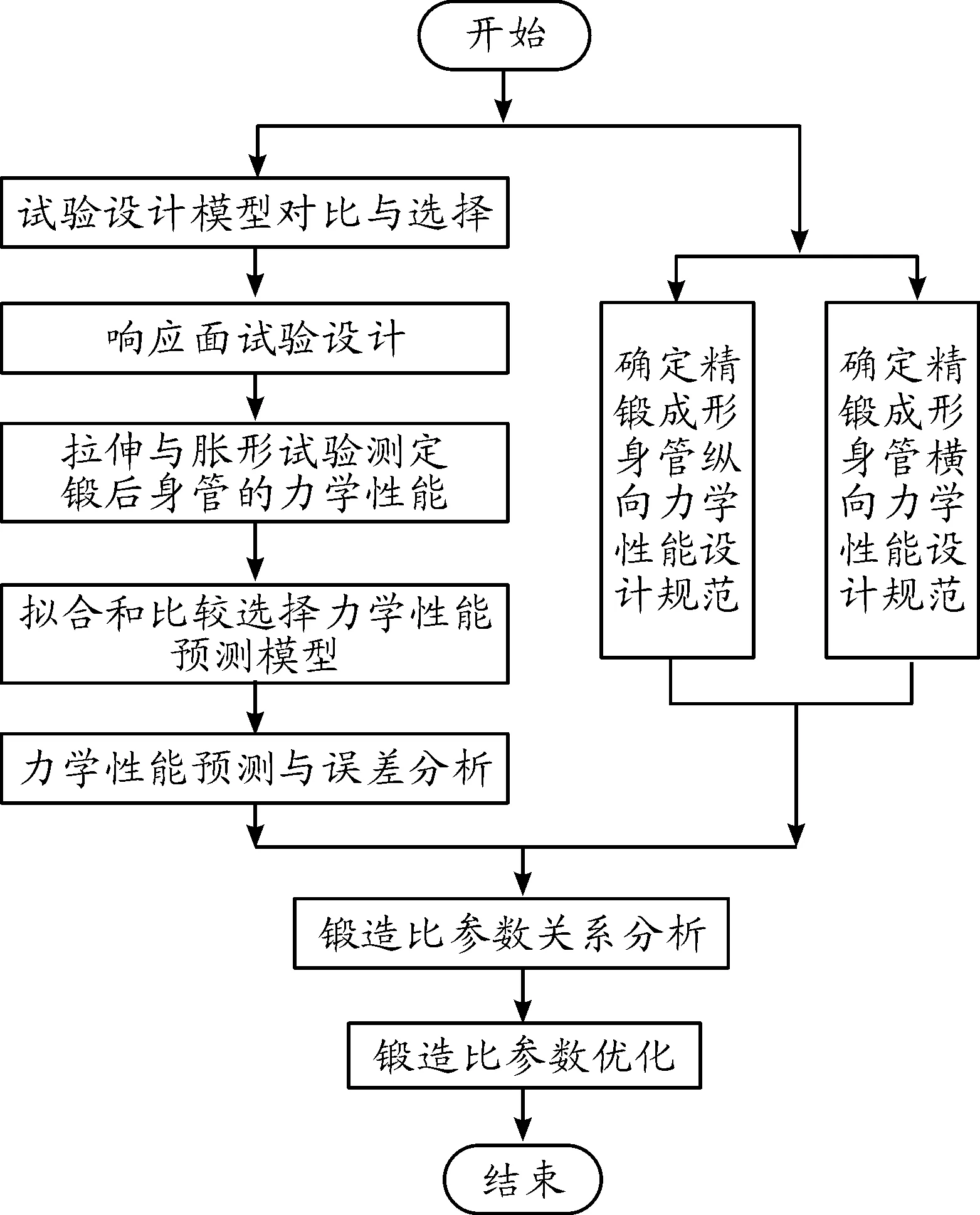
图1 身管性能分析与优化流程框图

为测定精锻成形身管力学性能数据，对身管进行性能试验，选择锻造过程参数不同的身管进行拉伸与胀形试验，测定了纵向屈服强度、纵向抗拉强度、纵向延伸率、纵向断面收缩率、横向屈服强度和横向延伸率，锻造过程参数与测量数据如表1所示(以横向延伸率为例)。

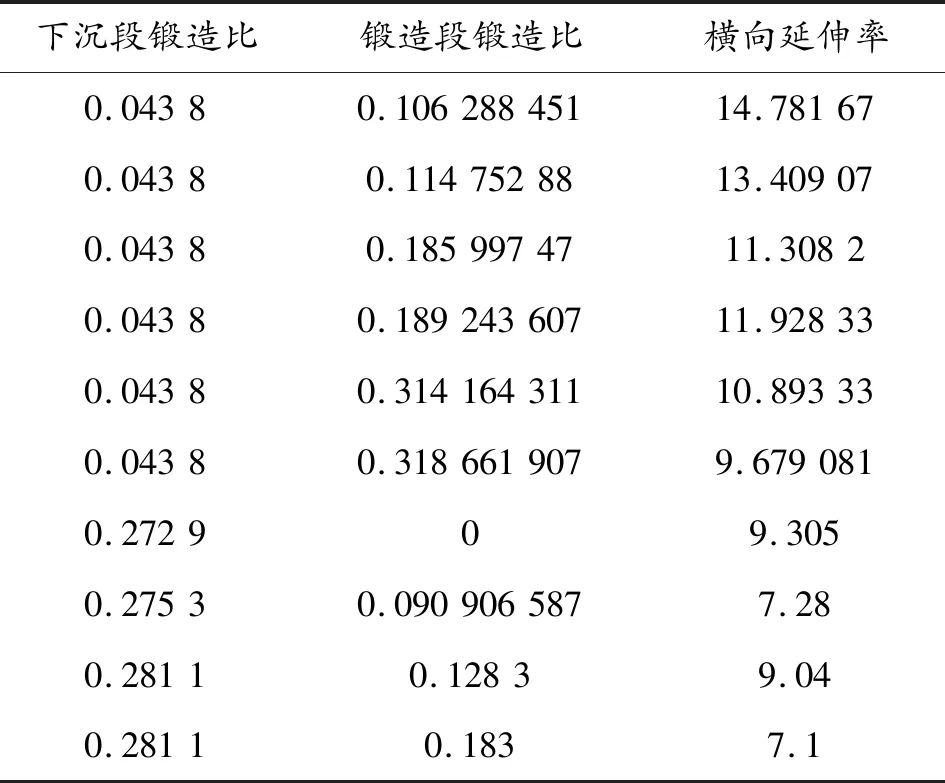
表1 试验测量数据 %

身管径向精锻过程是累积塑性变形，身管锻造比参数与弹塑性性能存在一定的关系。通过Design-Expert中的响应面分析可知，根据阶数的不同多项式有多种表现形式，根据是否考虑平方项和交叉项可分为Quadratic和2FI两种。

由试验数据和材料特性可知，横向延伸率值在7～15。在软件Radial Forge中对Quadratic模型拟合结果可知，多元非线性回归的残差平方和为 1.982 794 399 716 46，R2回归系数(模型拟合精度)为 0.964 464 624 643 217，拟合结果满足精度要求，但是在验证模型仿真与数据时发现横向延伸率畸变为负值，如图2所示，但是2FI模型不会发生，横向延伸率数值满足变化规律。

Quadratic函数模型使样本数据失真，力学性能值产生畸变，所以选择考虑交叉项而不考虑平方项的2FI模型。2FI函数模型的一般形式y1不仅考虑了下沉段锻造比和锻造段锻造比对锻后力学性能的影响，同时考虑了交叉项对锻后力学性能的影响，特殊形式y2则未考虑锻造比参数交叉项的影响。

y1=ax1+bx2+cx1x2+d

(1)

y2=ax1+bx2+d

(2)

x1为下沉段锻造比；x2为锻造段锻造比。

Design-Expert软件响应面分析分为两个部分，第一部分是Design，为了更匹配过程参数的设计规律，试验设计方法选择Miscellaneous，设计类型为Pentagonl，中心点为3，第二部分为Analysis，对拉伸、胀形力学性能数据运用非线性数据拟合方差获得响应面曲面方程并利用R2回归系数对拟合效果和有效性进行评估。R2回归系数表征模型拟合精度，并以此为依据选择拟合精确的模型。其中R2回归系数与性能指标成正比关系，系数越高拟合准确度越高。

(3)

式中：k表示试验设计组数；xi为响应面模型计算值；yi为试验数据值；yaver为试验数据平均值。

当多组力学性能数据拟合模型并选型时，每组数据拟合得到两种响应面曲面方程和两组回归系数。在多数据拟合模型选型时，对各组试验样本的参数求均值AVGi，利用参数AVGi表征模型拟合的准确度，如表2所示。

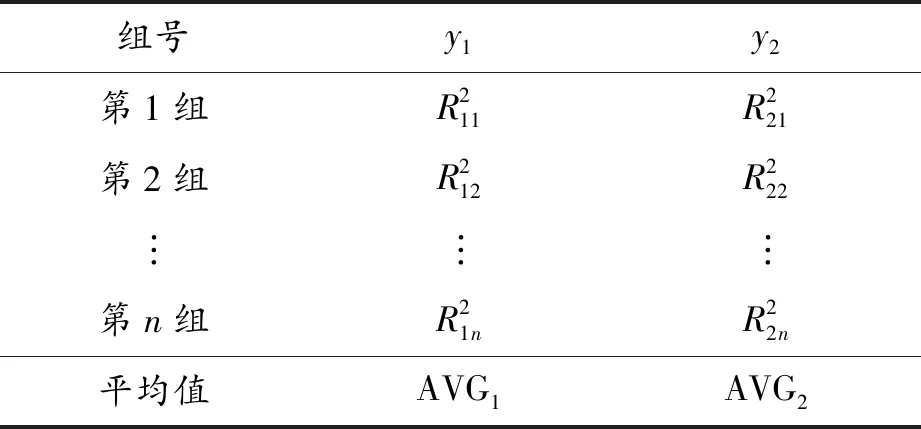
表2 拟合准确度

各组数据非线性拟合方程准确度均值为AVGi，AVGi由式(4)可得：

(4)

AVGi：表示同一组数据的R2回归系数均值；表征模型拟合精度，且与拟合效果和有效性成正比，值越大模型拟合越准确。

2 力学性能预测与误差分析

2.1 建立预测模型

对精锻成形身管进行拉伸、胀形试验得到力学性能数据，运用响应面函数表达式对试验数据拟合，并得到R2回归系数。由拟合结果可知，响应面曲面方程y1、y2拟合R2回归系数，方程y2拟合精度都高于y1，考虑下沉段锻造比和锻造段锻造比的参数交叉项提高了响应面拟合效果和可靠性，所以响应面拟合选择模型y1。

根据拟合响应面曲面方程可知锻后身管力学性能方程系数如表3所示。

表3 精锻成形身管方程系数

2.2 模型误差分析

身管内膛径向精锻成形是毛坯根据芯棒形状与尺寸在精锻机锤头高频率锻打下累积塑形变形的结果。在精锻成形中给定芯

棒和毛坯的设计尺寸，根据给出的锻件尺寸和过程参数使成形身管达到力学性能要求。

对试验身管毛坯进行编号记录毛坯参数，对锻造过程参数进行试验设计，选择实测直径为5.76 mm的芯棒在相同精锻成形过程下对毛坯锻打，记录试验数据，见表4所示。

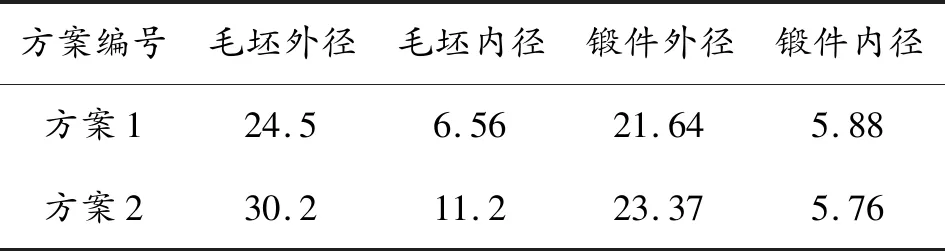
表4 方案编号 mm

根据毛坯、芯棒和锻件参数由锻造比公式可得各方案锻造比[5]：

下沉段锻造比公式：

(5)

锻造段锻造比公式：

(6)

精锻成形身管力学性能预测包括纯线膛精锻成形身管和弹线膛精锻成形身管预测两部分，为全面验证身管锻后力学性能预测的可靠性[13]，设计方案1为纯线膛身管锻件，方案2为弹线膛身管锻件。方案一总锻造比为22.12%，下沉段锻造比为4.3%，锻造段锻造比为18.60%；方案2总锻造比为34%，下沉段锻造比为28.11%，锻造段锻造比为8.12%。各方案力学性能误差分析如表5所示。

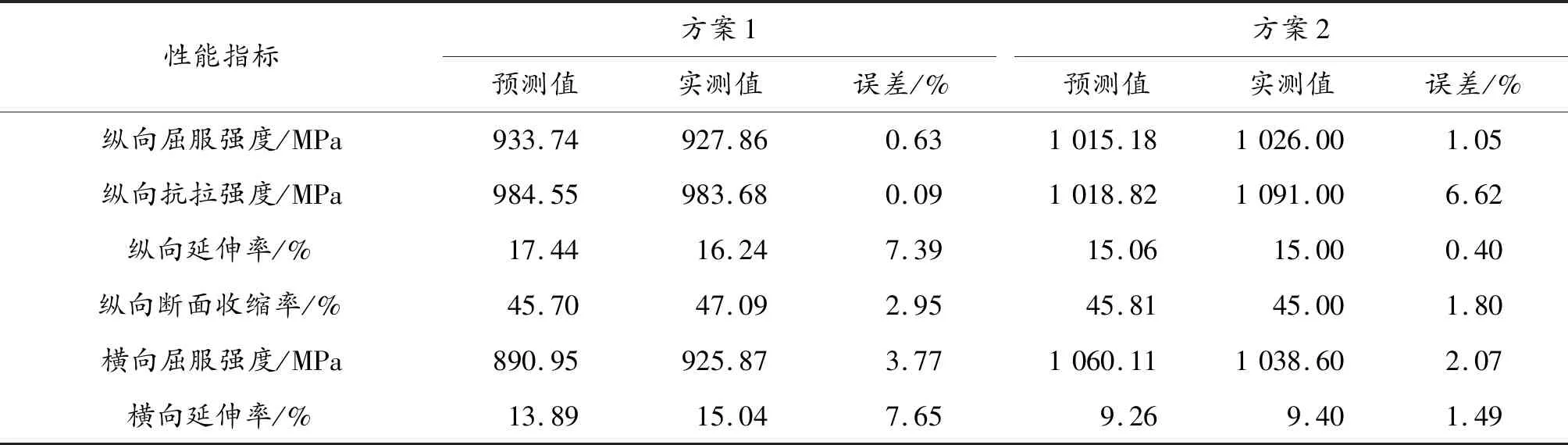
表5 各方案误差分析

由误差计算公式可知身管锻后力学性能预测值与实际值的误差小于10%(因样本有限，设置阈值为10%)，所以认为拟合响应面曲面方程是符合要求的。根据各方案预测结果可以得出弹线膛同锻预测误差小于纯线膛，所以弹线膛预测更准确。由大量试验结果可知，径向精锻过程对横向力学性能要求更高，弹线膛同锻力学性能预测误差在3%之内，所以预测与评估结果可靠性更高。

3 身管评估与过程参数优化

3.1 身管力学性能评估

为了确定精锻成形身管合格性评估规范，查询了步兵自动武器及弹药设计手册[11]关于纵向力学性能的要求，考虑到径向精锻过程横向力学性能对锻后力学性能的重要性，总结了大量试验结果，给出了身管锻后力学性能指标设计要求，如表6所示。

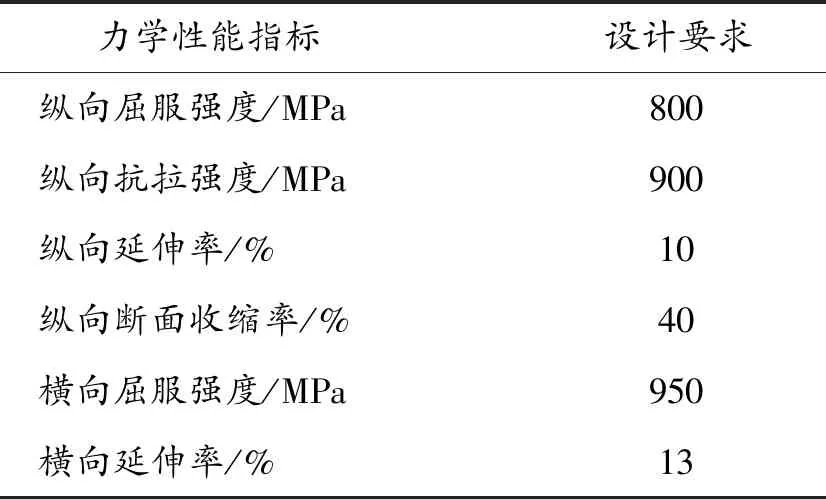
表6 轻武器结构钢力学性能指标

由试验验证方案与身管锻后力学性能设计要求可知，方案一与方案二的纵向力学性能都满足设计要求，但是方案一的横向延伸率满足要求而方案二的横向延伸率不满足要求，所以身管径向精锻过程着重考虑身管横向力学性能要求。

3.2 锻造比参数关系分析

精锻成形身管力学性能中横向性能是主要影响因素，根据横向延伸率的设计规范，得到锻造比参数关系与设计取值范围，如图3所示。

图3 锻造比参数关系图

由身管参数设计图可知散点为方块的曲线为身管横向延伸率合格时的边界曲线，当下沉段锻造比一定时，锻造段锻造比在曲线下方说明身管合格，在曲线上方说明身管不合格，同时也可对优化结果进行验证。

身管精锻过程给定了毛坯与芯棒参数，锻件的关键点径向尺寸由下压量决定，下压量由下沉段锻造比与锻造段锻造比决定，所以根据力学性能指标建立合格身管的锻造比参数设计图时，当下沉段锻造比一定时，可以得到锻造段锻造比合格区域，即下压量范围。

3.3 锻造比参数优化

1) 归一化处理

为了统一度量单位，加快训练网络的收敛性，把有量纲量变为无量纲量，将数据映射到0～1处理。

X=[x1,x2]T

(7)

(8)

2) 目标函数

为了得到最优过程参数，利用加权系数法将多目标优化问题转为单目标优化问题，优化目标为综合力学性能，在满足约束的情况下其值越大越好。

(9)

(10)

3) 约束

根据设计规范对各过程参数与优化变量约束如下：

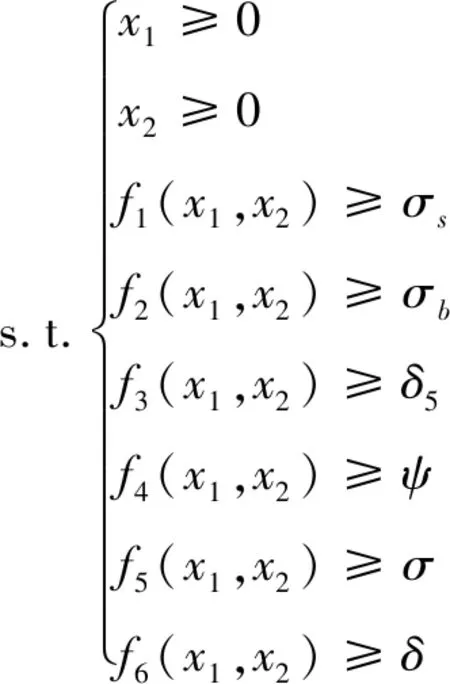
(11)

4) 优化

已知力学性能的响应面曲面方程，添加边界约束条件与横、纵向力学性能约束条件建立综合力学性能功能函数，采用非线性约束最小值优化[12]得到最优过程参数。

根据非线性约束优化可知下沉段锻造比为t1=0.148 7，锻造段锻造比t2=0.096 7，综合力学性能为fmax=0.59。由锻造比参数关系分析曲线可知，优化结果在合格范围之内，所以身管过程参数优化结果满足设计要求。同时参数t1远大于0，所以该锻造比属于弹线膛锻造过程参数，由弹线膛身管锻透极限图可知锻造锻造比边界值为7%[3]，所以参数t2为9.67%满足弹线膛同锻锻透极限。