基于收益管理的票额动态分配方案研究

王 洋,刘 斌

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

客运组织的核心目标是提高客票收益。目前由于客票分配计划的不合理性，往往会出现运能与实际需求不相匹配的现状，而客流的需求预测是票额分配的前提。由于铁路票额分配具有不确定性和时变性，因此，客流需求很难准确预测，导致预分的票额分配计划在售票后期与实际情况不相符。研究不确定性下的动态票额分配计划对于整个票额分配方案的实际可行性具有重要意义，并满足实际票额分配需求。

本论文研究的票额分配模型是基于客票收益最大化的目标构建，在考虑客流需求的不确定性基础上，建立单列车动态调整票额分配模型，后期在重要节点根据已确定模型对已有票额分配方案进行动态调整。这在一定程度上保证了旅客和铁路部门利益的均衡，在保证客座利用率的基础上，充分考虑了收益因素。一方面保证了旅客需求，另一方面最大限度地保证了铁路客运部门收益，在现有条件下力求达到二者均衡。

张瑞丰[1]在其学位论文中，基于收益管理理论，深入研究高速铁路票额分配问题。在客流预测方面，引入组合预测的思想将两种预测方法结合，使预测结果更加精确；在票额分配方面，先利用预测方法对客流进行准确预测，再以票额收入最大为目标建立票额分配模型[1]。曲思源、徐行方[2]等在《华东交通大学学报》期刊发表的论文中，提出了基于实际客流弹性票额分配方法，将随机需求以求其期望的形式转化为确定需求，建立了客票收益最大化模型。包云、刘军[3]在《中国铁道科学》期刊发表的论文中，基于时间因素将客流预测模型分为两部分：确定性需求和随机需求。而且利用期望值的概念，将随机需求合理变成了确定需求下的票额分配模型，一定程度上消除了因客流预测误差而产生的列车运能的浪费。北京交通大学的赵翔、赵鹏和李博[4]将目光关注在多列车票额分配问题的研究上，在他们发表的关于高速铁路票额的论文中，基于多列车、多停站方案条件建立票额分配模型，以全线票额最大为约束建立了整数规划模型，设计粒子群算法对模型进行求解，此方法可以整个高速铁路线路为主体进行收益优化。他们还从旅行时间最少的角度出发，探究了列车的差异性对票额分配产生的影响，建立了双目标优化问题，分别以铁路部门客票收益最大化和旅客旅行时间最短两个方面为目标函数，最大化铁路和乘客的系统效益。包云、刘军[5]等提出为减少短途车流对长途的车流的侵占，可使用“嵌套式”的票额分配模型，用长途车流的票额套用短途车流的票额，以此来合理保障长途车流的有效票额，此模型利用蚁群算法求解。华北电力大学的李建一[6]在其学位论文中，利用设计改建的BP神经网络算法进行客流预测，借鉴航空业的经验将收益管理应用于高铁票额分配，根据分巢式和非巢式两种情况分别建立模型，并采用不同方法求解。北京交通大学的宋文波、赵鹏和李博[7]不仅考虑了列车的运行时间，还考虑了旅客舒适度以及各列车停站方式的差异，考虑到铁路部门和乘客的整体情况，综合考虑二者的优势，旨在最大限度地发挥效益，由此建立考虑旅客出行时间的高铁列车车票分配的非线性整数规划模型，该模型通过模拟退火算法求解。西南交通大学的刘华森、程文明、张铭奎[8]以列车客座利用率及客票受益最大为目标，运用改进过的遗传算法对优秀的子代进行迭代，以逆向思维求解各途径车站的票额分配，并与此同时完成了旅客列车客座的分配和组合优化。北京交通大学的赵飞[13]从影响铁路客票的多重因素，包括定价因素、定价理论及定价方法入手，基于国外票价机制，结合中国铁路票价现状，提出了两阶段计划票价定价模型。其中第一阶段先将旅客在市场条件下进行详细分类并由此建立客票的运算模型。第二阶段将客运产品等级分类，着重考虑此条件下的客票优化模型。

1 模型建立

铁路客运受到经济、地域等环境因素的影响，同时节假日和平时的客流量相差较大，导致不同OD间的客流千差万别，且无法用确定的数据代替。实际客流量往往是按照某种确定的概率分布，比如正态分布、偏态分布、泊松分布等。将动态的客流需求与动态的票额分配方案相结合，按照高铁客流分布特点，充分利用高铁列车运能，在考虑需求随机性的前提下，将其转化为求非线性规划问题，从而实现高铁列车收益最大化。

1.1 模型假设

假设各OD是正态分布下的随机客流需求，列车的编组数量、车辆型号及定员是固定的，列车载客能力固定，同一等级相同OD票价固定，且不考虑折扣，全部票额分配至运行线路上的停靠站出售，不考虑预留等特殊情况，不考虑退票或超售的情况，且只研究单方向的客流需求预测。

1.2 模型建立

假设一条高速铁路上共有m个区段和m+1个停靠站，每个OD的客流需求服从正态分布，路径(i,j)的客流需求密度为

(1)

式中：x为从起售时刻开始经过的时间，fij(x)为OD段(i,j)的客流需求密度函数，uij为OD段(i,j)的客流需求平均值，σij为OD段(i,j)的客流需求标准差。

根据客流需求密度函数，运用客票期望销售量的计算方法可求得该列车在该OD上的客票期望销售量为

(2)

式中：aij为截止x时刻OD段(i,j)的已分配票额，初始值设为客流初始需求。

则基于收益最大的目标函数为可表示为

(3)

式中：pij为OD段(i,j)的票价。

由于编组能力固定，且不考虑超载情况，则需满足列车最大能力约束Cmax，即

(4)

为保证各个OD段的票额分配限制在合理范围内，可取参数α=0.8，β=1.2，将票额限定在期望附近波动

αuij≤aij≤βuij.

(5)

综上所述，票额分配模型为

(6)

(7)

1.3 动态约束

与此同时，在售票期内选取节点，根据已售票额，对每个OD的已分配票额进一步约束，即

dij≤aij≤Cmax.

(8)

式中：dij为所取节点OD段(i,j)的已销售票额。

综上所述，动态调整下的票额分配模型为

(9)

(10)

2 求解算法

随机需求下的票额分配模型由于借助了客流概率密度这一数学概念，假设客流服从正态分布，在概率密度的基础上，利用积分将客流密度转化为客票期望销售量。模型相比较线性规划更加符合实际情况，但模型也更加复杂，由线性规划转变为非线性规划。对于此类问题，采用粒子群算法求解。

2.1 算法思想

此算法的设计思想是模拟群鸟觅食规律。每只鸟位置、前进方向均随机，只凭借个体经验和群体的共享信息联系，并向共同的目标前进。

每只鸟可通过自身经验和群内信息判断当前位置相对于目标位置距离，即适应值。与此同时，每只鸟都可记住自己的当前最佳位置，称为局部最优。此外，每只鸟可以记住整个鸟群找到的最佳位置，即全局最优，通过搜索全局最优附近的区域使整个鸟群的中心不断接近于全局最优。

2.2 算法优势

粒子群算法主要有以下优势：

对已初支完毕的背后存在的空洞和不密实处进行注浆回填，如预留注浆孔出现堵塞，可重新打设，打设要求按设计图纸进行，初期支护施工时,应在拱部120°范围内预埋φ42mm钢花管作注浆管，壁厚3.25mm,长0.8m。注浆管间距1.0m×1.0m，梅花型布置，即对初衬背后压注水泥浆。

1)对问题信息的依赖程度低，采用实数求解方法，算法通用性强。

2)需要设计和调整的参数较少，易于实现，这是粒子群算法最明显的优势。

3)搜索理念先进，采用协同搜索思想，同时利用局部和全局信息引导搜索。

4)收敛速度快，对计算机硬件尤其是CPU和内存要求不高。

5)具有飞越性的特点，能够越过搜索区域上信息严重不足的障碍，飞越局部最优，达到全局最优。

2.3 算法流程

粒子群算法的运算流程如下：

1)确定粒子的属性，包括速度、位置、惯性因子及加速常数。设定迭代次数，同时确定算法终止条件。

3)确定局部最优值对应的位置为局部最优位置，全局最优对应的位置作为全局最优值所处位置，即目标函数可行解。

4)通过比对局部最优、全局最优以及当前粒子的速度来更新粒子速度和位置。并进行限幅处理，使其处于合理范围。

5)比较每个粒子的当前值和最优值，若更优，则进行替代数值和位置的替代。

6)在所有局部最优值中找出全局最优值，并更新对应位置作为全局历史最优值的所在位置。

7)重复4)～6)，直至达到1)中设定的迭代次数或终止条件。

8)得到粒子群最终的全局最优值，及其对应位置和各粒子最终的局部最优值及对应位置。

2.4 算法理论

粒子群算法在搜索过程中需要依照下列算式，对所有粒子的速度和位置不断进行更新。

式中：k=1,2,3,…,m,n=1,2,…,N；ω为负数惯性因子负数；加速常数c1和c2为非负常数；r1和r2为在[0，1]内的随机数；α为更新位置时，控制速度的权重约束因子。

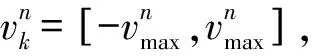
不同问题设定不同的迭代终止条，一般达到预定的最大迭代次数或粒子群搜索的全局最优适应值不高于目标函数的可接受最小误差。

2.5 模型应用

3 算例分析

3.1 算例简述

以兰州西开往西安北的D2684次列车为例，该列车从兰州西客站始发，途经定西北、秦安、天水南站、宝鸡南站到达西安北站。列车采用8节编组，为简化计算只考虑列车二等座席的载客能力，每趟列车二等坐席的最大载客能力为560人。本例中用于计算客票收入各区段(OD)的票价如表1所示。

表1 列车各OD票价 元

假设客流服从正态分布，各区间客流预测均值、标准差如表2、表3所示。

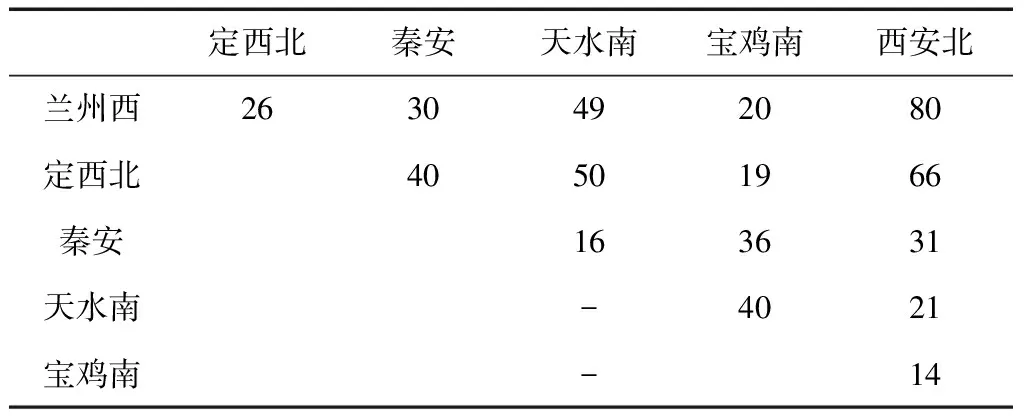
表2 列车各OD客流预测均值 人

表3 列车各OD客流预测标准差

3.2 算例求解

设定粒子群规模m=50，迭代次数N=100，学习因子c1=c2=2.05，惯性因子ω=0.4。

个体适应度与迭代次数的关系如图1所示，票额分配的最优求解结果如表4所示。

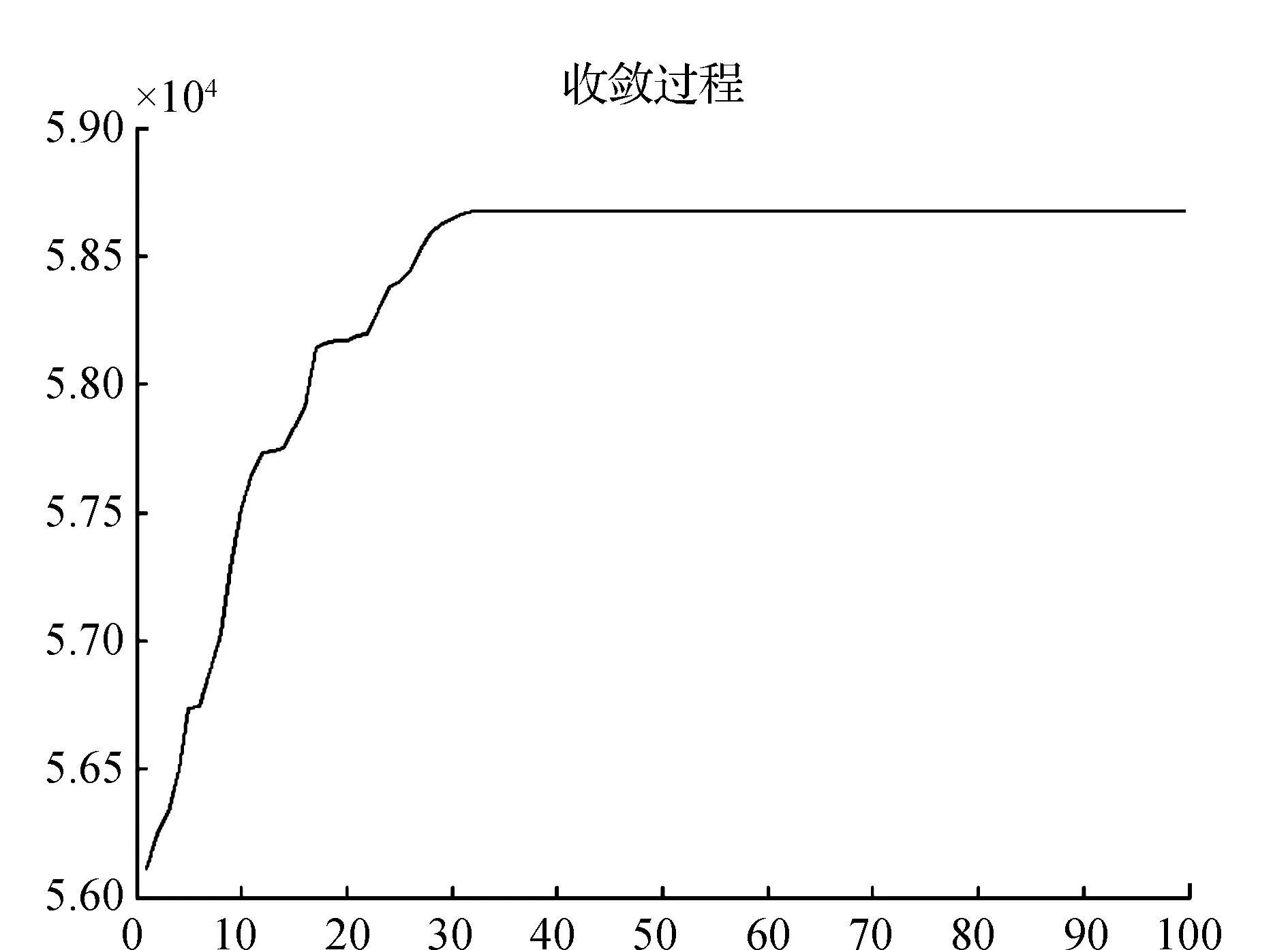
图1 迭代求解过程

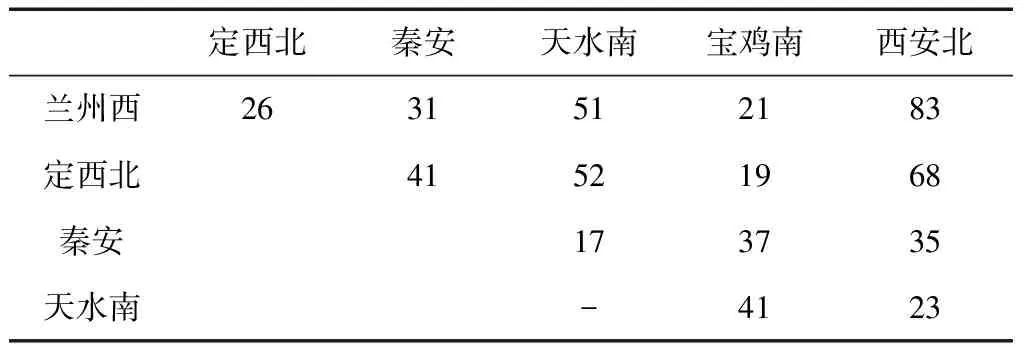
表4 票额分配最优结果 张

由上可知，当粒子迭代至40代左右开始出现收敛，直至100代粒子的适应度函数基本保持不变。迭代结束时粒子所处的位置就是本问题寻找到的一个满意解，可以看出，分配结果尽量满足了长途客流需求，按此票额分配方案可求得总的票价收益为58 920元。

选取某一段时间内的购票数据进行分析。表格内的数字代表从预售期开始至当天累积售出的票额，预售期售票数据如表5所示。

表5 节点售票数据 张

设定粒子群规模m=50，迭代次数N=1 000，学习因子c1=c2=2.05，惯性因子ω=0.4。

个体适应度与迭代次数的关系如图2所示，调整后的票额分配最优结果如表6所示。

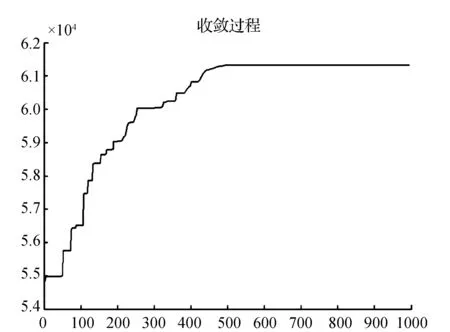
图2 调整后迭代求解过程

表6 调整后票额分配最优结果 张

由上可知，当粒子迭代至700代时粒子适应度函数基本保持不变。迭代结束时粒子所处位置即最终优化结果，计算得总票价收益62 718.5元。不难看出，以相同的客流需求为基础，尽管预售期已售票额在一定程度上影响了分配结果，但在满足长途客流需求的基础上对票额进行调整，期望收益提高约6.4%，因此，该动态调整方案可行。

4 结 语

本文研究了单列车多停靠方案的动态调整票额分配方案，根据建立的模型采用粒子群算法求解，并根据实际算例对模型算法进行求解。结果表明，调整后的分配方案收益高于原方案收益，提高了列车票额收入，实现需求与供给的相对均衡，最大限度地利用了列车运能。