考虑受灾点差异性的应急物资配送方案研究

冯江博

(兰州交通大学 交通运输学院，甘肃 兰州 730000)

近几年我国自然灾害频发，如2019年的四川凉山三县的森林火灾灾害，以及不久前发生的四川宜宾地震灾害，还有6月13日发生的江西洪灾灾害。其中，2008年的汶川地震是近几年来发生的影响最大、造成损失最严重的自然灾害事件。而且随着社会的发展，一旦发生大型自然灾害会对社会的经济活动造成较大的影响和损害，所以，人们对应急救灾的要求越来越高。为此，我们需对应急资源和设施进行合理配置，确保灾害发生时能够进行快速有效的救援，以减少灾害造成的损失。

应急资源优化配置的研究内容丰富，本文主要从设施的选址、模型算法和物资配送三个方向展开探讨。其中对应急物资配送方案的研究一直是该领域的研究热点。Kemball-Cook D等[1]指出建立应急管理系统，及时高效地开展应急救援行动具有重要意义。陈旭哲[2]考虑了路段危险程度、救援时间限制和最少物资需求等因素,建立了应急物资配送模型。郑云水，穆然等[3]建立了多应急点、多救援点和多种资源的动态多阶段资源调配模型，并得到了最优应急物资调配方案。詹沙雷，刘南[4]考虑了应急物资储备库对受灾点的覆盖限制，将统计决策与运筹规划相结合进行研究。李双林，马祖军等[5]在应急需求不确定的情境下，建立了震后应急物资多式联运配送模型。Huijun Sun等[6]提出了一种双层规划模型，上层模型是通过最小化成本为目标来确定应急设施的位置，下层模型是通过最小化运输成本来实现均衡的需求分配。刘明，赵林度[7]分析了点对点配送模式和枢纽辐射模式的优势，建立了混合协同配送模型。孙昌玖，裴虹等[8]引入应急物流配送中心横向转运作业方式，建立应急物资协同调度模型。王付宇，李琰[9]对应急物资调度、灾后应急物资的选址-分配，不同约束下的应急物资调度及双层规划等研究现状进行了梳理，并提出了改进建议。

综上所述，既有研究大多集中在储备库的选址和应急物资的配送路径选择上，对应急物资配送研究方面也主要考虑就近配送模式，而较少考虑受灾点和受灾程度的差异性。本文在考虑各个受灾点需求紧迫程度差异的基础上，引入受灾点需求紧迫系数这一参数，提高应急物资配送方案的公平性及合理性，建立多目标应急物资配送模型，并运用NSGA-Ⅱ算法进行求解。

1 受灾点需求紧迫程度

进行应急救灾活动时，各受灾点的受灾程度不同，各灾区的应急需求紧迫程度也会不一样。在现实情景中，考虑到应急物资储备库的物资储备量有限，在应急物资储备库可能缺货的情况下，如果仍按照就近原则进行应急物资配送，对于受灾情况较重、需求更加紧迫的受灾区群众来说很不公平，容易引发群众不满情绪。因此，救灾时应充分考虑受灾点和受灾程度的差异性，先确定各个受灾点的需求紧迫程度，对紧急程度较大的受灾点优先进行物资配送。只有确定了受灾区域的需求紧迫程度，才能做到有重点、有主次地进行应急物资发放，从而充分发挥应急物资的效用，公平地进行物资配送。

1.1 指标体系及权重确定

影响受灾点的需求紧迫程度的因素可分为确定性因素和模糊性因素两种，综合考虑文献[10]和文献[18]，建立以道路破环程度、物资短缺程度、物资需求量、受灾人口数量和受灾应急损失为评价指标的需求紧迫程度评价指标体系。充分考虑各指标之间的差别，利用熵值法和AHP法分别确定指标的客观和主观权重，并通过线性加权法获得最终权重值。需求紧迫程度评价指标体系如表1所示。

表1 需求紧迫程度评价指标体系

1.2 基于B型关联度TOPSIS法的物资紧迫程度评价方法

TOPSIS法具有对样本无特殊要求、能够充分利用数据、计算简单、能够对每个对象的优劣进行排序的优点。同时，由于应急救援工作存在较多不确定因素，因此，本论文采用改进过的TOPSIS法——B型关联度TOPSIS法综合评价模型——来确定受灾点的需求紧迫系数。评价方法的具体计算步骤如下：

1.2.1 构建决策矩阵

假设第i个受灾点对第j项指标的指标值记为xij(i=1,2,…,n;j=1,2,…,m)，n个受灾点的指标值记为初始评价矩阵X。可通过式(1)来构建标准化矩阵

(1)

式中：max(Xj)为矩阵X中第j项指标的最大值。

1.2.2 确定正负理想解

用熵值法、AHP法及线性加权法确定组合权重W=(w1,w2,…,wm)的值 ,将决策矩阵C与权重W相乘，获得加权决策矩阵R=(Rij)n×m，并计算得出正负理想解，具体如式(2)和式(3)所示。

正理想解

(2)

负理想解

(3)

1.2.3 确定B型关联度

(4)

(5)

(6)

(7)

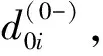
1.2.4 确定需求紧迫系数

先获得第i个受灾点的B型关联度之间的相对贴进度ζ1，并进行归一化处理，再用式(8)来确定受灾点需求紧迫系数

(8)

2 模型的构建

本文在根据应急物资需求紧迫程度确定受灾点应急物资配送的优先级基础上，建立以应急物资分配方案公平性最大化和受灾点的需求满足率最大化为目标的应急物资配送多目标模型，具体描述如下：

2.1 假设条件

1)应急物资储备库的储备总量小于受灾点的需求总量；

2)应急物资储备库之间不发生应急物资的流转；

3)应急物资储备中心有足够的运输工具来完成运输任务，且只考虑运输工具满载的情况；

4)不考虑应急物资多样性和运输工具多样性的情况。

2.2 模型符号与含义

I为应急物资储备库集合，i∈I；D为受灾点集合，j∈J；Xij为从应急物资储备库i运至受灾点j的物资量；dj为受灾点j所需物资的数量；Ci为应急物资储备库i的库存容量；λj为受灾点的紧迫系数；α为受灾点的最小满足率。

具体模型为

(9)

maxZ2=maxα;

(10)

(11)

(12)

(13)

(14)

0≤α≤1.

(15)

目标式(9)表示应急物资分配方案的公平性最大化；目标式(10)表示受灾点的需求满足率最大化；约束式(11)表示应急物资储备库i运到受灾点的应急物资的量不能超过储备库i的库容量；约束式(12)表示受灾点获得的物资不应大于其需求的量；约束式(13)表示资源不足；约束式(14)表示α为各个受灾点的需求满足率的最小值；约束式(15)表示需求满足率α的取值在0～1之间。

3 NSGA-Ⅱ

NSGA-Ⅱ是当下最流行的解决多目标问题的遗传算法之一，它在传统的遗传算法基础上降低了算法的复杂性，运行速度更快，解的收敛性更好[9]。NSGA-Ⅱ的基本思想可描述为:

1)随机产生一个初始种群，进行非支配排序后通过选择、交叉和变异操作得到子代种群；

2)将父代种群与子代种群合并,进行快速非支配排序,并对排序后的个体进行拥挤度计算,依据非支配关系和个体的拥挤度选择并生成新的父代种群；

3)重复步骤1)和步骤2)的过程，直到满足结束条件为止。

NSGA-Ⅱ的程序流程如图1所示。

图1 NSGA-Ⅱ算法流程

4 算例分析

4.1 问题描述

参考文献[10]，将芦山县、宝兴县、天全县、雅安市名山区、雅安市雨城区、荥经县、汉源县、蒲江县和丹棱县作为受灾点。将兰州、西安、武汉、昆明作为应急物资储备库地。查询相关统计年鉴、新闻报道可以获得受灾点的需求量，如表2所示，储备库的库存量如表3所示；通过文献调研和专家评价的方式得到受灾点的评价指标数据，其中道路破坏程度、物资短缺程度数据由专家评价得到，评价层次为很严重、严重、一般、轻和很轻，本文分别用9、7、5、3和1将其转化为确定值，具体如表4所示。通过1.2的方法可以得到受灾点需求紧迫系数值，如表5所示。

表2 受灾点的需求量 t

表3 应急物资储备库的储备量 t

表4 受灾区评价指标

表5 受灾点的需求紧迫系数

4.2 模型验证分析

基于MATLAB R2018b实现NSGA-Ⅱ算法。设置初始种群为80，迭代次数为500。令受灾点的总体满足率最小为85%。算法运行的过程和结果如表6所示。

由表6可知应急物资储备库配送至各受灾点的应急物资数量和目标函数值的结果，其中受灾点应急物资最小满足率为87.19%，紧缺程度最小为30.05 t，而物资需求紧迫程度最大的芦山县应急物资满足率达到了99.7%，即在满足了最小应急物资满足率的情况下，对应急物资需求更紧迫的受灾点进行优先满足。说明当应急物资储备库库存量小于受灾点的需求量时，考虑受灾点的紧迫程度，按

表6 应急储备库配送方案及指标运行结果 t

照优先级的顺序对受灾点进行物资配送，并满足最小满足率，可有效进行物资分配，即从兰州市、西安市、武汉市和昆明市向芦山县、宝兴县、天全县等受灾点进行配送，优先对芦山县进行应急物资配送。

5 结束语

本文针对灾后应急物资的配送问题，考虑应急物资储备库的储备量小于受灾点需求量的情况，在既有研究基础上，为提高应急物资配送方案的公平性，引入了受灾点的需求紧迫系数这一参数，优先满足紧迫程度较大的受灾点，并使受灾点的满足率保证在一定水平，建立了多目标应急物资配送模型。以芦山地震为案例，运用NSGA-Ⅱ算法对模型进行求解，获得了最优配送方案。但本文依然存在一些不足和局限，在应急物资配送研究的基础上，考虑多种情景、多种应急物资的情况还有待进一步研究。