基于力法的斜拉桥静力计算
2020-06-06李海霞
李海霞,张 程
(1.安徽新华学院 土木与环境工程学院,合肥 230088; 2.中铁四局建筑公司,合肥 230088)
斜拉桥是常用于大跨度公路桥,主要有索、塔柱和主梁三部分组成,是一种桥面体系受压支承体系收拉的多次超静定结构,由于斜拉索的弹性支承作用,大大减小了主梁横截面的弯矩,使得斜拉桥向着更大跨径的桥梁发展。[1]目前对斜拉桥使用阶段的静力学计算研究很少,大部分是基于有限元软件进行数值模拟,而建模过程较复杂,且要输入大量数据,结果不容易收敛,计算单元多,工作量较大。[2-3]一般情况下斜拉桥的近似的结构分析方法:选择斜拉桥主梁弯矩作为赘余力;将斜拉桥的主梁作为支撑于一系列弹性支撑上的连续梁;选择索力作为多余未知量。[3]但这些方法只能得到近似值,不能得到精确解。张云峰利用QR法对斜拉桥进行静力学分析[4-5],该方法理论知识较难理解,且编程量大。本文利用结构力学中的力法[6]推导出斜拉桥在使用过程中的拉索内力和梁弯矩内力,计算过程中未知量较少,并通过语言编程,能够得到精确的计算结果。
1 斜拉桥分类
以梁结构为基本体系而延续的斜拉桥,可看成在梁基础上加支承塔和斜索而构成的多次超静定体系,根据梁的形式不同分为以下几种。
1.1 悬浮体系斜拉桥
主梁为两端简支梁,除两端外,全部用缆索吊起,如图1所示。
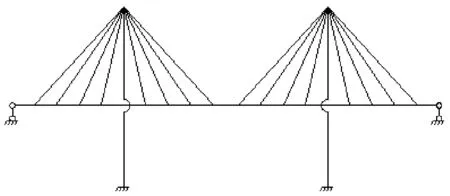
图1 悬浮体系斜拉桥计算简图
1.2 支承体系斜拉桥
主梁在塔墩上有支点,此时梁有中间铰,即:在三跨简支梁上由塔和斜索吊起,如图2所示。
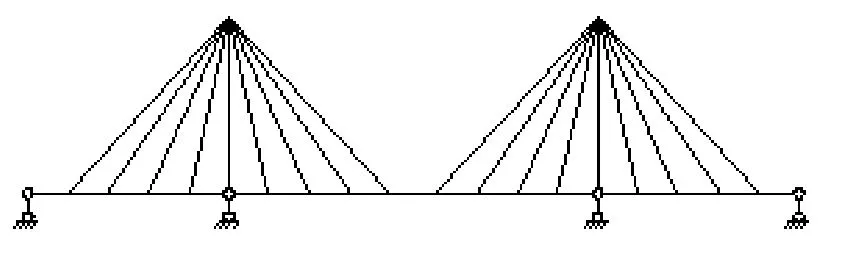
图2 支承体系斜拉桥计算简图
1.3 塔梁固结体系斜拉桥
三跨连续梁上加索塔和拉索,如图3所示。
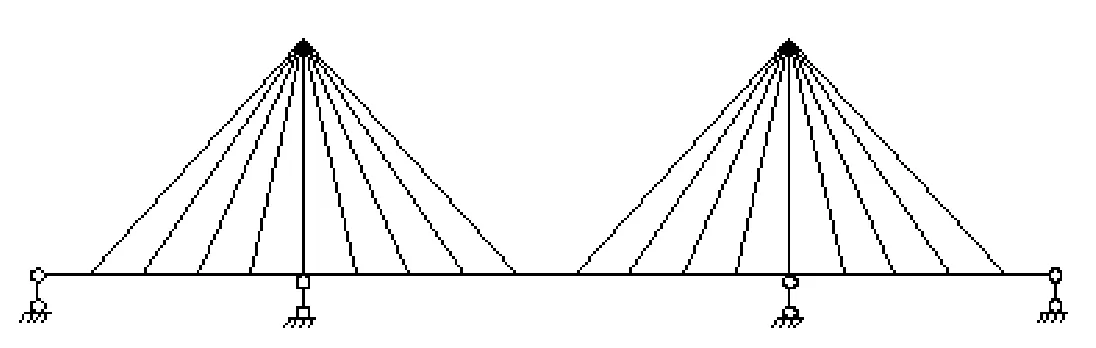
图3 塔梁固结体系斜拉桥计算简图
1.4 刚构体系斜拉桥
塔、主梁、柱墩相互固结,加斜索构成超静定体系,如图4所示。
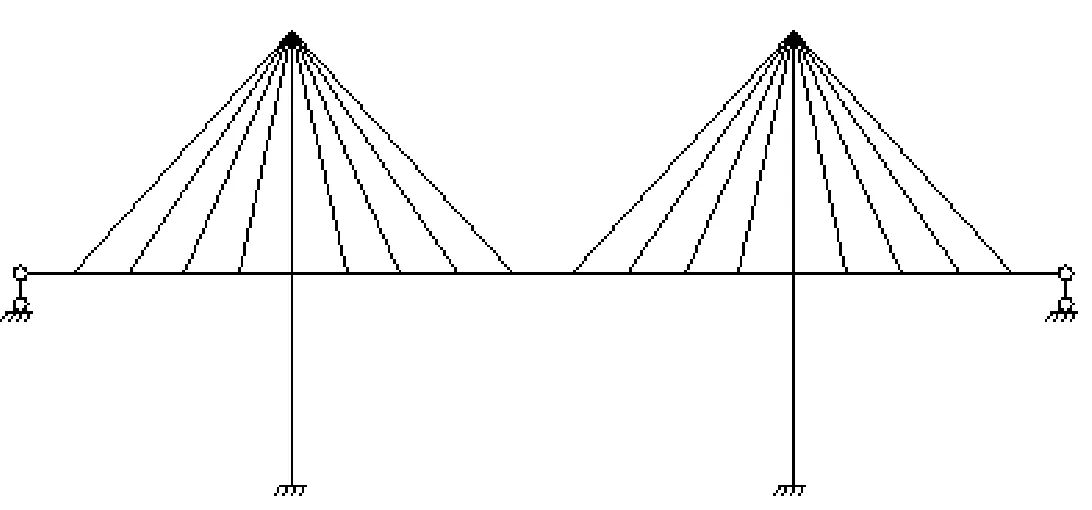
图4 刚构体系斜拉桥计算简图
同等跨度,同等拉索数,悬浮式斜拉桥力学计算工程量最大,但计算公式规整,便于编程,现以此形式讲解计算过程,其他形式在计算时只需要进行一些简化便可。
2 斜拉桥力学计算
2.1 悬浮体系斜拉桥
2.1.1 未知量的确定
斜拉桥力学计算模型为:在索梁相交处将梁截断换成中间铰,中间铰处弯矩为力法未知量xi。
2.1.2δij、δji、δii和Δip的确定
δij、δji、δii和Δip的计算式皆由三部分组成:
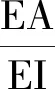
2.1.3 结构计算简图
根据对称性取半边结构,将各刚节点换成铰节点,各段梁的长度为d,各根拉索的长度分别为l1、l2…ln截面弯矩作为力法的未知量,不计塔压缩变形,塔顶看成固定铰,如图5所示。
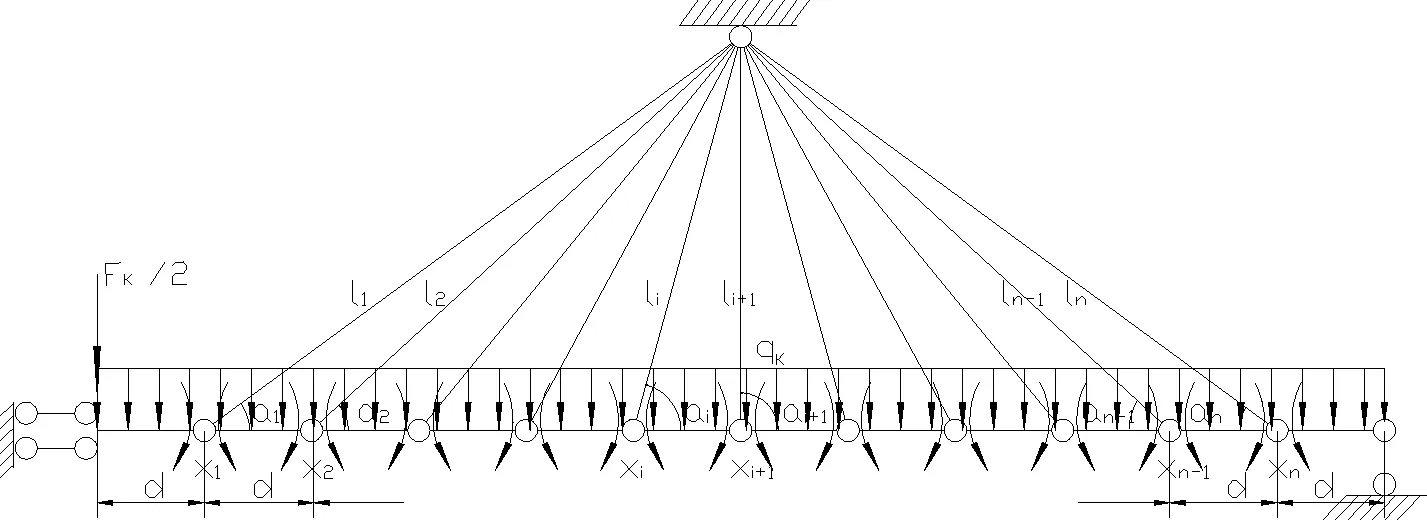
图5 力法基本体系
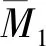
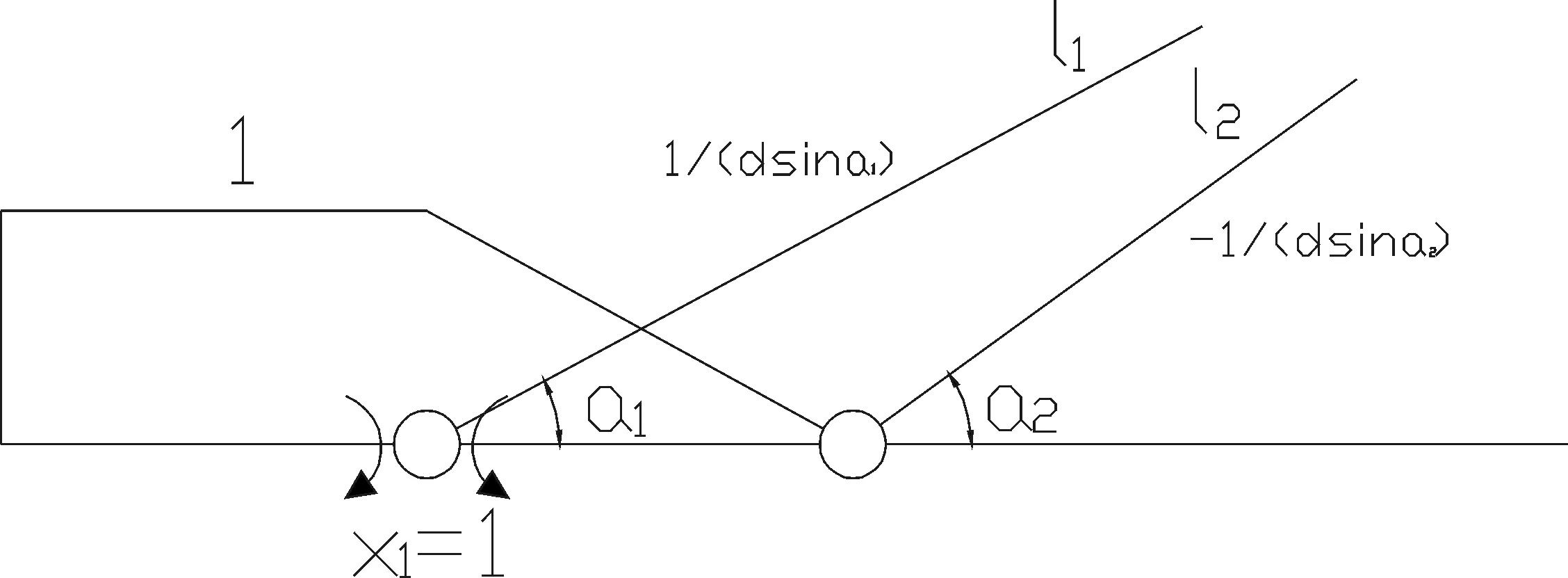
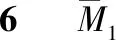
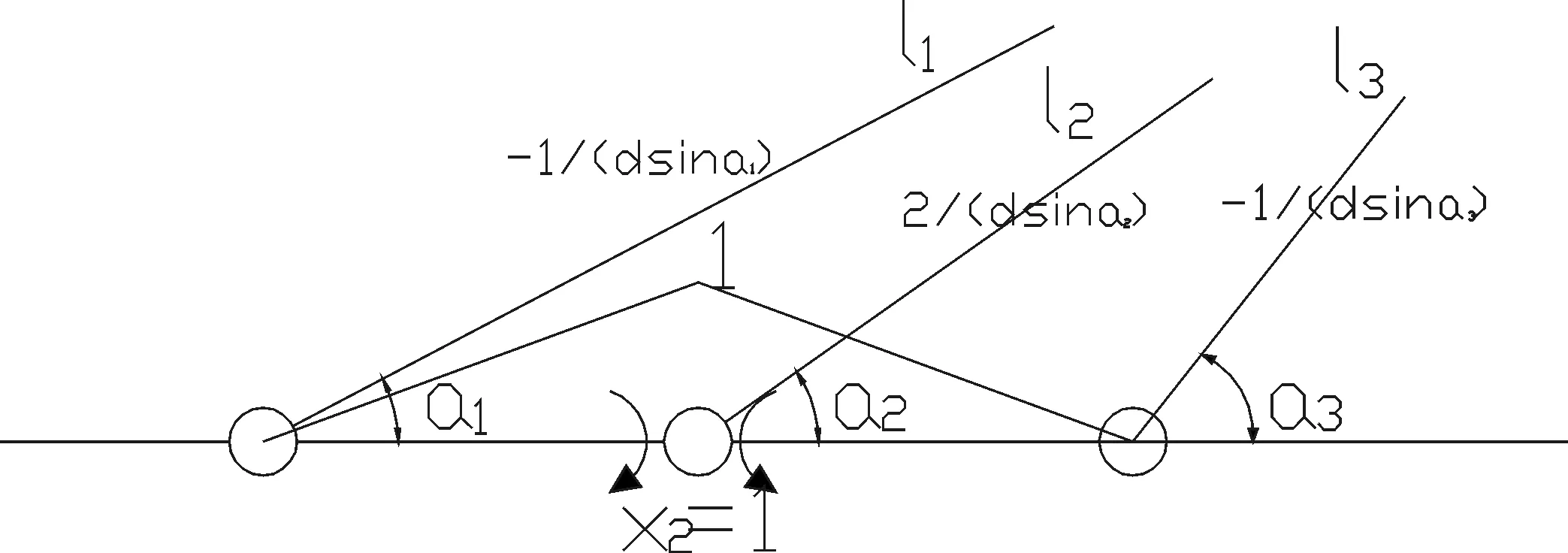
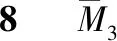
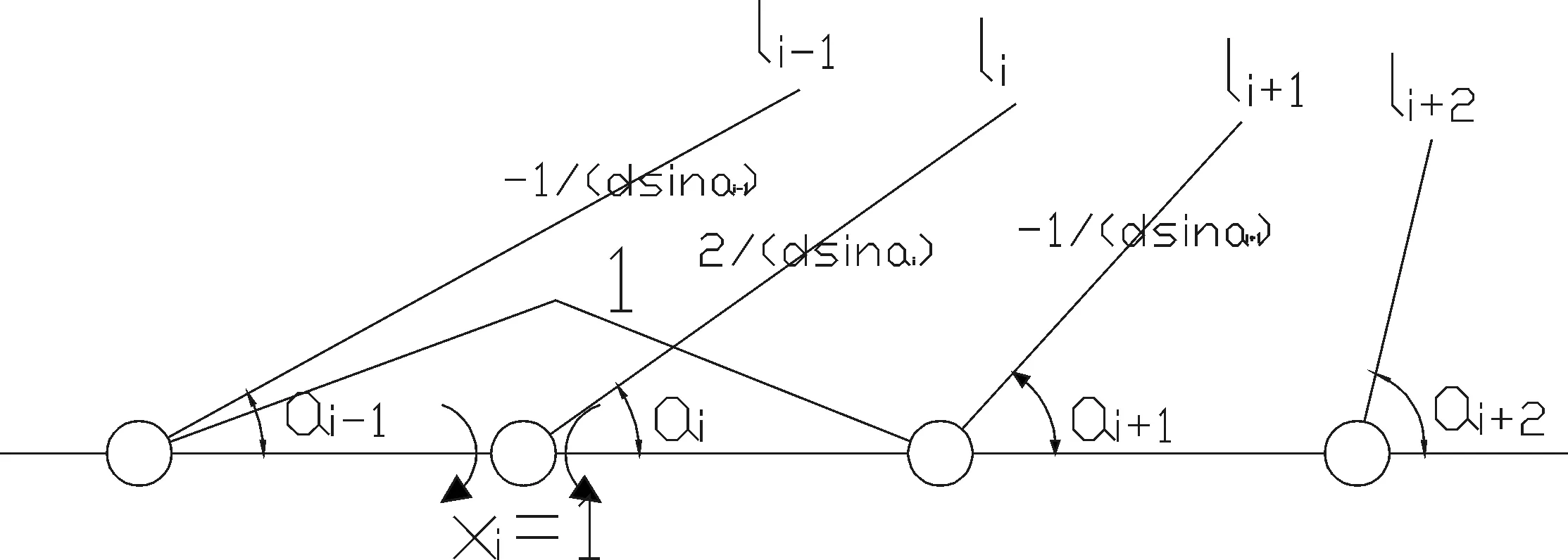


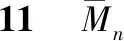
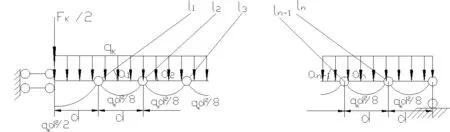
图12 MP图、FNP图
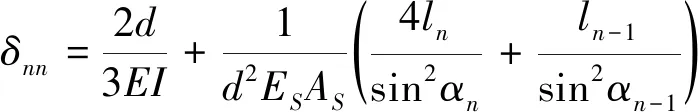
一座百米以上的斜拉桥,几十根斜拉索则有几十个力法求解未知量,利用对称性后,未知量的个数也有近二十个,导致力法方程就有十几个以上的代数方程组,但每行系数为:δi,i-2,δi,i-1,δi,i,δi,i+1,δi,i+2这五个量不等于0,其他的系数全等于0,故称为五弯矩方程式,此种带宽为五的方程组求解可以利用编写程序完成。
力法方程组为:{f}nn{xi}+{ΔiP}={0},未知量xi求出后,由下面各式求出各拉索的拉力。
柱塔所受到的轴向压力F=∑FNisinαi,柱塔所受到的水平拉力较小。
对于(2),(3),(4)三种形式的斜拉桥,只需要对(1)所示斜拉桥的五弯矩方程式进行刚减即可。
2.2 支承体系斜拉桥
2.3 塔式固结体系斜拉桥
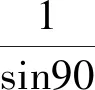
2.4 刚构体系斜拉桥
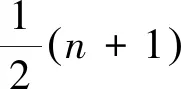
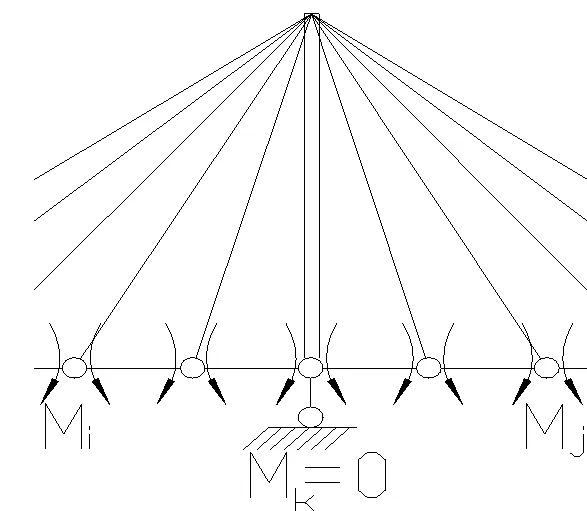
图13 支承体系斜拉桥力法基本体系图 图14 刚构体系斜拉桥力法基本体系
3 悬浮体系斜拉桥计算举例
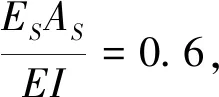
计算得li,sinαi如表1所示。
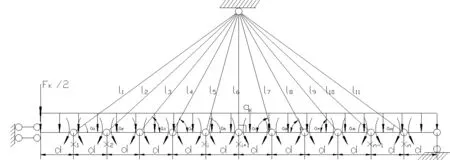
图15 悬浮斜拉桥力法基本体系

i1234567891011li58.3095042.42636.05531.6223031.62236.05542.4265058.309sinαi0.5140.60.7070.8320.9481.00.9480.8320.7070.60.514
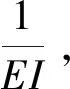
系数矩阵:
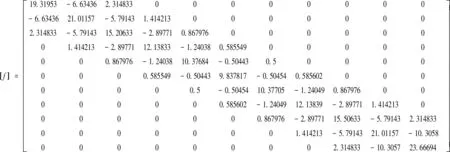
常数项行列式:
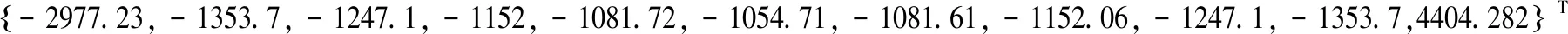
通过编写的程序计算得未知量行列式为:
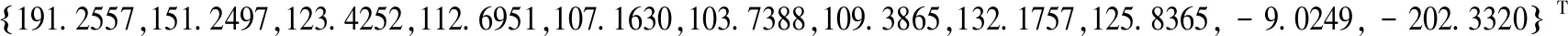
利用计算出来的{x}算得斜拉索拉力行列式为:
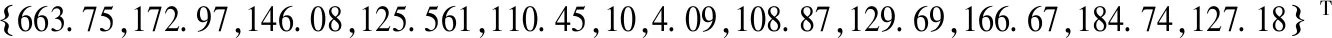
最终做出弯矩图如图16所示。
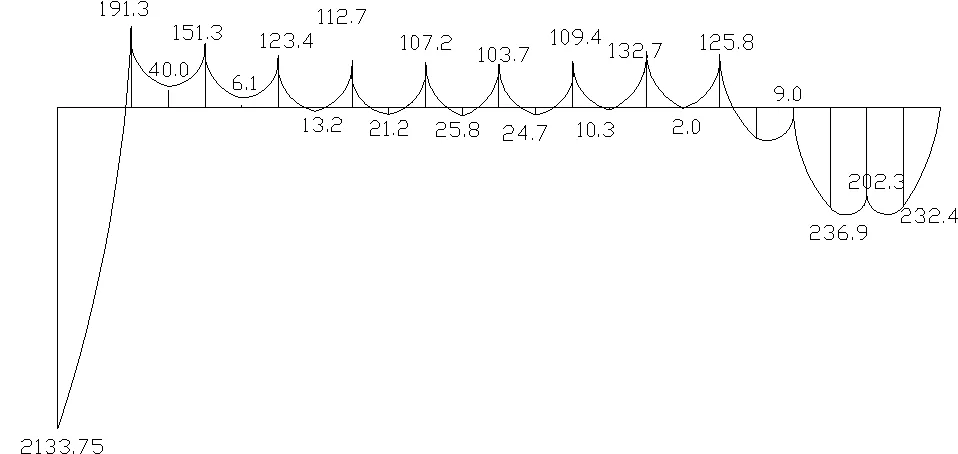
图16 弯矩图/KN·m
4 总 结
本文的计算原理是结构力学中已经较为完善的理论:力法,其推导过程较为简单易懂,再利用FORTRAN语言完成计算工作,解决了未知量较多时计算工程较庞大的问题,计算结果精确。
